基于带跳的O-U过程的彩虹期权定价
2018-01-09石方圆杨立保李翠香
石方圆, 杨立保, 李翠香
(1.河北师范大学 数学与信息科学学院,河北 石家庄 050024; 2.邢台学院 数学与信息技术学院, 河北 邢台 054001)
基于带跳的O-U过程的彩虹期权定价
石方圆1, 杨立保2, 李翠香1
(1.河北师范大学 数学与信息科学学院,河北 石家庄 050024; 2.邢台学院 数学与信息技术学院, 河北 邢台 054001)
文章假设标的资产价格服从带跳的Ornstein-Uhlenback(O-U)过程,无风险利率r(t)为时间的确定函数,波动率σ为常数,利用保险精算方法给出了彩虹期权的定价公式。
Ornstein-Uhlenback(O-U)过程;泊松过程;彩虹期权;保险精算
0 引 言
近年来,随着全球金融市场的迅猛发展,期权在衍生证券中的地位显得尤为重要,其定价问题也是金融数学的核心问题之一,受到越来越多的国内外学者的关注和研究。目前又出现了各类奇异期权,如亚式期权、复合期权、交换期权、选择期权、彩虹期权[1]等。这些奇异期权的灵活性和多样性是常规期权所不能比拟的。彩虹期权就是讨论2个风险资产的最大值或最小值期权。资产最大值彩虹期权在到期日T的收益为:
max{ωmax[S1(T),S2(T)]-ωK,0},
资产最小值彩虹期权在到期日T的收益为:
max{ωmin[S1(T),S2(T)]-ωK,0},
其中,ω=±1。当ω=1时为看涨期权;当ω=-1时为看跌期权。
许多金融产品的定价可以转化为2个风险资产的最大值或最小值期权的定价,例如外币期权、选择权债券等。因此探讨彩虹期权的定价公式是很有意义的。
文献[2]假设股票价格服从几何布朗运动,给出了彩虹期权的定价公式。股票价格服从几何布朗运动,意味着随着时间的变化,股票价格收益率将只朝同一方向变化(上升或下降),然而实践证明,股票的期望收益率具有均值回复性,是不可能随时间朝同一个方向变化的。为克服几何布朗运动的缺陷,许多学者在研究期权的定价公式时假设股票价格服从Ornstein-Uhlenback(O-U)过程[3-5]。
另外,在真实的资产市场中,一些重要事件的发生会引起股票价格产生间断性跳跃,因此股票价格包括持续扩散和不持续跳跃2个方面。文献[6]研究了带有跳扩散过程的普通欧式期权定价。之后许多学者给出了一些期权在跳扩散模型下的定价公式[7-10],其中,文献[10]得到了跳扩散模型下彩虹期权的定价公式。
假设股票价格服从带跳的O-U过程将更具有实际的意义,然而目前关于这方面的研究很少。因此,本文将考虑标的资产价格服从带跳的O-U过程的彩虹期权的定价。
传统的期权定价方法通常假设金融市场是无套利、均衡、完备的,这与实际市场不太吻合。文献[11]首次提出用保险精算方法给期权定价,将期权定价问题转化为等价的公平保费问题,无任何经济假设。其基本思想是:无风险资产按无风险利率折现,风险资产按期望收益率折现。本文将用保险精算方法给出彩虹期权的定价公式。
1 金融市场模型
假设彩虹期权中2个资产价格满足如下方程:
dSi(t)=Si(t)[(μi-λiθi-αilnSi(t))dt+
σidBi(t)+φidNi(t)],i=1,2
(1)
其中,μi、λi、θi、αi、σi为常数;B1(t)、B2(t)为相关系数为ρ的布朗运动;Ni(t)为资产价格在时间段[0,t]内随机跳跃的次数,它是参数为λi的Poisson过程;φi为第i种资产价格跳跃的相对高度,ln(1+φi)服从正态分布,即
φ1、φ2、N1(t)、N2(t)相互独立且独立于B1(t)、B2(t)。
用φij表示第i种资产发生第j次跳跃时的相对高度,假定φi1,φi2,φi3,…为相互独立的且与φi同分布的随机变量序列,无跳跃发生时记为φi0=0。
当φ1=φ2=0时,方程(1)为O-U过程;当φ1=φ2=α1=α2=0时,方程(1)为几何布朗运动。
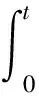
定义2 执行价格为K,到期日为T的资产最大值彩虹期权在0时刻的保险精算价格定义为:
资产最小值彩虹期权在0时刻的保险精算价格定义为:
引理1 假设资产价格Si(t)满足方程(1),则有:
(2)
证明先假定在[0,t]之间没有发生跳跃。由Ito公式可得:
d(eαitlnSi(t))=
(3)式两边从0到t积分并整理得:
假定只在T1∈[0,t]时刻发生了一次跳,则有:
当跳的次数为Ni(t)时,则有:
引理1得证。
引理2 假设Si(t)满足方程(1),则资产价格过程Si(t)在时间[0,t]上产生的期望收益率为:
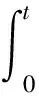
证明由(2)式可得:
当φi0=0,j≥1时,E[1+φij]=1+θi,则有:
将(5)式代入(6)式中可得:
将(7)式代入定义1中可知,引理2得证。
引理3 假设(X,Y)为二维联合正态分布的随机变量,则有:
其中,I{·}为示性函数;μX、μY分别为X、Y的期望;σX、σY分别为X,Y的标准差;ρXY为随机变量X、Y的相关系数;a、b为常数。
证明首先证明当μX=μY=0,σX=σY=1时,有
E[ecXI{X>a,Y>b}]=
其中,c为常数。事实上,经计算可得:
E[ecXI{X>a,Y>b}]=
[(x-c)2-2ρXY(x-c)(y-ρXYc)+
其中
所以(9)式成立。
其次证明(8)式,由于
E[eXI{X>a,Y>b}]=
取c=σX,由(9)式可得(8)式。
引理3得证。
2 彩虹期权的定价公式
下面研究资产最大值彩虹看涨期权的保险精算定价。
定理1 假设Si(t)满足方程(1),则到期日为T,执行价格为K的资产最大值彩虹看涨期权在0时刻的期权价值为:
其中
证明因为
max{max[A1,A2]-K,0}=
max{A1-K,A2-K,0}=
(A1-K)I{A1>K,A1>A2}+(A2-K)I{A2>K,A2>A1}=
A1I{A1>K,A1>A2}+A2I{A2>K,A2>A1}+
KI{A1 所以 把前3项分别记作Π1、Π2、Π3,下面分别估计它们。 由(2)式、(4)式可得: 其中 因为 ⟺ 所以 因为 所以由引理3可得: 从而 S1(0)(1+θ1)m× 同理可得: 综上,定理1得证。 利用相同的方法可证出其他3种彩虹期权的定价公式。 定理2 假设Si(t)满足方程(1),则到期日为T,执行价格为K的资产最大值彩虹看跌期权在0时刻的期权价值为: 证明由于 max{K-max[A1,A2],0}= max{min[K-A1,K-A2],0}= (K-A1)I{K>A1,A1>A2}+(K-A2)I{K>A2,A2>A1}= KI{K>A1,K>A2}-A1I{K>A1,A1>A2}-A2I{K>A2,A2>A1}, 类似定理1可得定理2。 定理3 假设Si(t)满足方程(1),则到期日为T,执行价格为K的资产最小值彩虹看涨期权在0时刻的期权价值为: 证明由于 max{min[A1,A2]-K,0}= max{min[A1-K,A2-K],0}= (A1-K)I{A1>K,A2>A1}+(A2-K)I{A2>K,A1>A2}= A1I{A1>K,A2>A1}+A2I{A2>K,A1>A2}-KI{A1>K,A2>K}, 类似定理1可得定理3。 定理4 假设Si(t)满足方程(1),则到期日为T,执行价格为K的资产最小值彩虹看跌期权在0时刻的期权价值为: 证明由于 max{K-min[A1,A2],0}= max{max[K-A1,K-A2],0}= (K-A1)I{K>A1,A1 -A1I{K>A1,A1 KI{A1>K,A2>K}+K, 类似定理1可得定理4。 当φ1=φ2=α1=α2=0,定理1~定理4的结果与文献[1]中的结果一致。 对新型期权进行合理定价已经成为金融数学研究的重要内容之一。至今为止,很多专家学者取得了丰硕的研究成果。本文在这些研究的基础上,在O-U过程下加入跳跃,同时包含了资产收益率的均值回复性和跳跃对期权价格的影响,用保险精算方法给出了彩虹期权定价公式。得到的期权定价公式扩展了文献[1]中的结论,而且本文结论还可以进一步扩展至多资产最优或最差选择期权的定价。另外,还可以在此基础上进一步考虑利率随机的情况。 [1] 张光平.奇异期权[M].2版.马晓娟,任涤新,蒋涛,等.北京:机械工业出版社,2014:312-315. [2] STULZ R M.Options on the minimum or maximum of two risky assets[J].Journal of Financial Economics,1982,10(2):161-185 [3] 严海峰,刘三阳.广义 Black-Scholes 模型期权定价新方法——保险精算方法[J].应用数学与力学,2003,24(7):730-738. [4] 刘兆鹏,刘钢.基于O-U过程具有不确定执行价格的期权保险精算定价[J].杭州师范大学学报(自然科学版),2011,10(4):316-319. [5] 赵攀,肖庆宪.随机利率下 O-U 过程的幂型欧式期权定价[J].合肥工业大学学报(自然科学版),2014,37 (11):1386-1390. [6] KWOK M K.Mathematical models of financial derivatives[M].Berlin:Spinger Press,2008:151-153. [7] 钱晓松.跳扩散模型中亚式期权的定价[J].应用数学,2003,16(4):161-164. [8] 钱晓松.跳扩散模型中交换期权的定价[J].扬州大学学报(自然科学版),2004,7(1):9-12. [9] 陈晓航,王玉文.带常数跳跃模型下的欧式期权定价[J].哈尔滨师范大学自然科学学报,2015,31(3):25-27. [10] 盛冠楠.跳扩散模型下极值期权的定价[D].桂林:广西师范大学,2011. [11] BLADT M,RYDBERG H T.An actuarial approach to option pricing under the physical measure and without market assumptions[J].Insurance Mathematics and Economics,1998,22(1):65-73. PricingofrainbowoptionsunderOrnstein-Uhlenbackprocesswithjump SHI Fangyuan1, YANG Libao2, LI Cuixiang1 (1.School of Mathematics and Information Science, Hebei Normal University, Shijiazhuang 050024, China; 2.School of Mathematics and Information Technology, Xingtai University, Xingtai 054001, China) The underlying asset price process is supposed to follow the Ornstein-Uhlenback(O-U) process with jump, the riskless interestr(t)bethetime-dependentfunctionsandthevolatilityofthestockσbeconstant.Thepricingformulasofrainbowoptionsaregivenbyusingactuarialapproach. Ornstein-Uhlenback(O-U) process; Poisson process; rainbow option; actuarial approach 2016-06-29; 2016-10-11 国家自然科学基金资助项目(11571089) 石方圆(1991-),女,河北邢台人,河北师范大学硕士生; 李翠香(1971-),女,河北磁县人,博士,河北师范大学教授,硕士生导师,通讯作者,E-mail:cuixing-li@126.com. 10.3969/j.issn.1003-5060.2017.12.025 O211.6 A 1003-5060(2017)12-1714-05 (责任编辑张 镅)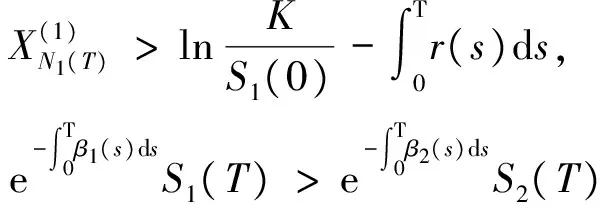
3 结 论
