城市老中心区空间形态影响因素的评价理论及方法研究
2018-01-09王彦辉
汪 亮, 王彦辉
(1.南京工程学院 建筑工程学院,江苏 南京 211167; 2.东南大学 建筑研究所,江苏 南京 210096)
城市老中心区空间形态影响因素的评价理论及方法研究
汪 亮1,2, 王彦辉2
(1.南京工程学院 建筑工程学院,江苏 南京 211167; 2.东南大学 建筑研究所,江苏 南京 210096)
文章在分析影响城市老中心区空间形态主要因素的基础上,建立了相对应的一级评价指标和二级评价指标,综合模糊评价方法对城市老中心区建筑模型、公共空间模型和交通模型3个方面进行权重确定,并将权重与城市区域网络的变化建立函数关系,在函数图像中与各个一级指标的最佳舒适值进行对比,进而确定在某个合适的区域面积内城市空间形态的最佳状态。最后,文章以杭州市上城区老中心区为典型案例验证了该文提出评价方法的科学性,为城市规划和管理提供了决策依据。
城市老中心区;空间形态;影响因素;综合模糊评价;函数关系
随着城市中心区第三产业迅速发展,中心区的区位价值也相继释放和显现出来,多数城市开展了城市中心区的综合改建工程,如上海中心商业区、天津中心区、广州中心区、南京中心区和合肥旧城中心区规划等。然而,近年来伴随者经济结构的转变和国家对城市发展战略的政策引导,城市中心区再开发迎来了重要转型期,较之以往,目前城市老中心区再开发面临的挑战更加严峻,主要体现在功能结构、组织系统、环境要求等各个方面。
面对城市规划和区域协调的整体框架,目前对于城市老中心区的研究多停留在宏观层面上,关于其再开发的引导策略和相关具体技术以及问题成因的分析较少。事实上,国内外对于城市形态的研究有较多理论方法。文献[1]总结了一百多年来国内外城市空间形态研究的谱系及各个时期的基本特征;文献[2]则基于空间句法,从图论的角度研究了中微观层面的城市空间形态,在分析城市空间整体关联性基础上通过伯明翰实践为城市形态的复杂性研究提供了理论基础和方法;文献[3]通过实验方法构建了城市空间形态紧凑度模型,用城市标准化紧凑度指数客观反映了城市空间形态的利用情况,实验证明标准指数越接近1,城市形态越趋近圆形,空间利用率越高。文献[4]从社会、经济、制度、资源环境等几个方面列举对比了中国大量中心城市的空间特征,探析了城市空间绩效的变化趋势、影响因素及变化动力机制。综上所述,已有相关文献主要是对城市空间形态的整体性和服务性进行评价以及构建评价体系,本文则从城市老中心区空间形态的影响因素入手,通过建立评价指标和权重,针对老中心区既有的普遍特点,通过函数关系直观反映适宜的空间形态下各影响因素的状况,为城市老中心区再开发空间形态的实践提供理论依据。
1 空间形态影响因素的评价原理
城市老中心区空间形态特征复杂,具有建筑密度大、老旧建筑多、城市公共空间零碎、形态多样、人均土地少、交通量大、功能结构倾向性明显等特点,而造成这些特点的主要因素可以具体到建筑模型、公共空间模型、交通模型3个一级评级因子上,3个一级因子又受各自的3个二级因子制约。评价逻辑是从二级因子的数据整理计算中获得一级因子的实际现状评价指标,通过专家论证获得的舒适评价指标值h=(h1,h2,h3)与实际获得的一级因子评价指标值i=(i1,i2,i3)进行对比,在函数图像中清晰地描述平均现实状况在平均水平指标上下的弹性浮动,从而指导对现有空间在科学评价的基础上实现设计改造。
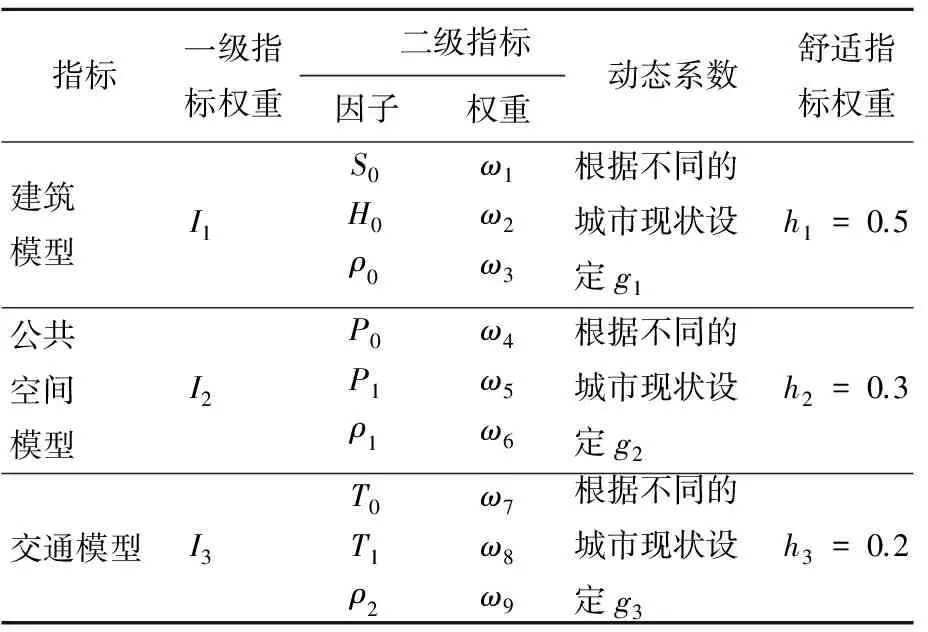
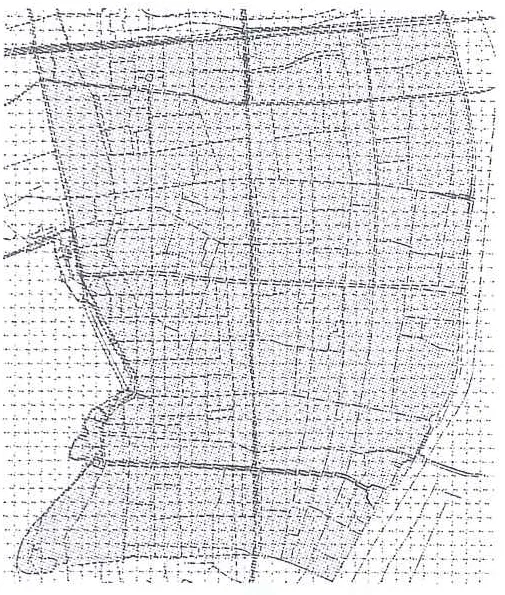
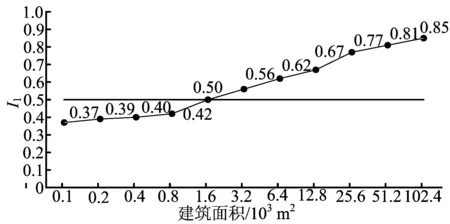
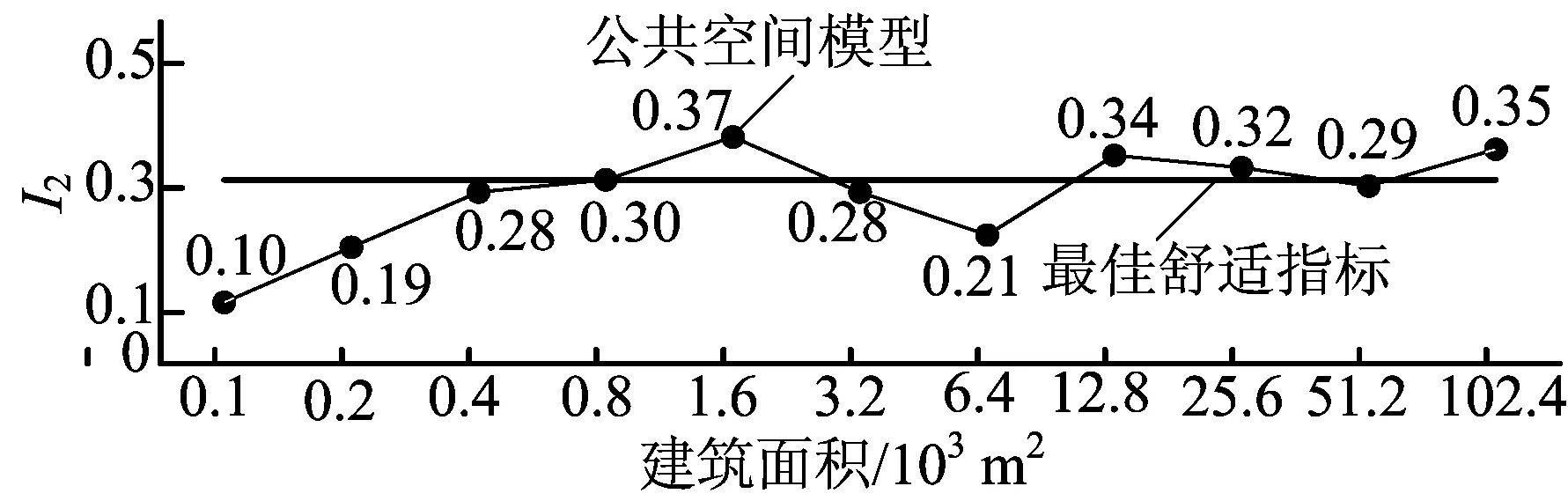
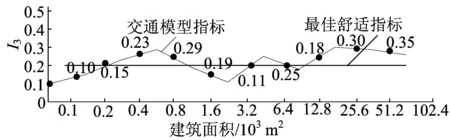
关于数据的获取和函数关系的变量划定是将城市老中心区的地理信息系统(geographic information system,GIS)图像按照不同大小的方格网状进行区域划分(100 ×100,200×200,400×400,800×800,1 600×1 600,3 200×3 200 ),在不同面积的区域内各个评价因子的状况有所变化,而这种变化与方格大小相关,因此将一级评级因子和方格网作为函数的2个变量。因为有关评价指标因子的评价值和权重数获得都是基于综合模糊评价基础之上的,同时还要在评价的过程中考虑到城市空间形态的动态变化因素[5],所以本文研究在计算过程中加入了动态变化系数g=(g1,g2,g3),g值的确定是根据具体城市的发展状况而定的,一般情况下城市老中心区的动态变化不会超过原状的1/2,因此本文g的取值范围为0.5 城市老中心区由于历史条件的原因,建筑组成多元并存,建筑体量、风格、形态等特征要素共同构成了现行的建筑模型,具体可以划分为3个二级评价因子,即建筑尺度、建筑高度、建筑密度[6],首先建立3个因子的数据指标。 2.1.1 建筑尺度 建筑尺度体现了中心区建筑在三维空间中与人及其他建筑的体验对比关系,是一个相对概念,但是在人和建筑互为对象的过程中,将人视为参照对象,将建筑的平均体积作为考量建筑尺度的指标,体积越大说明建筑尺度越大,指标计算公式如下: 由(1)式可以推导出老中心区建筑尺度的指标可以表示为: 2.1.2 建筑高度 建筑高度体现在老中心区建筑轮廓的竖向变化上,不同高度的建筑通过一定的秩序形成丰富的城市天际线,一方面突显了高出建筑所在区域在整个空间中的核心地位,加强了空间的标示性;另一方面通过突出竖向的高度也指明了平面空间的方向性,设定了空间坐标系。对于给定的建筑总面积,底层建筑面积越小,建筑高度就越大,建筑高度的指标计算公式如下: 2.1.3 建筑密度 建筑密度是反映在一定区域内建筑对总用地面积的占用情况,体现了公共空间与建筑实体部分与所占总用地的配比,在城市老中心区再开发过程中,控制好建筑密度能有效释放公共空间活力,同时适当的建筑密度能够起到调节老中心区空间环境的自然通风。建筑密度指标计算公式如下: 其中,ρ0为建筑密度;S2为总用地面积。 城市老中心区的公共空间普遍存在场地零散、街巷尺度小且曲折多变、空间界面多样、市民活动集中等特点,在老中心区街巷空间是公共空间的核心,之外还有广场、绿地以及一些次生空间[6],因此本文将公共空间模型的评价内容归结为街巷尺度、街巷曲折度、公共空间密度3个二级因子。 2.2.1 街巷尺度 街巷尺度是将街巷和人互为对象形成的动态对比体验效果,因为与建筑不同,街巷的实体空间部分是抛开建筑界面的二维空间,所以街巷尺度的主要指标体系为街巷面积的分布情况,具体指标计算公式如下: 2.2.2 街巷曲折度 街巷曲折度反映了街巷空间组成的复杂程度,曲折度越大街巷空间形态越丰富,但是在承担一定功能基础上,过分复杂的空间形态会带来交通不利、消防疏散困难等一系列问题,因此对街巷曲折度的控制应该根据实际情况适度确定,影响街巷曲折度的主要因素为街巷总长度和街巷端点直线距离,曲折度指标计算公式如下: 其中,P1为街巷曲折度;l为街巷端点直线距离;L为街巷总长度。 2.2.3 公共空间密度 公共空间密度与建筑密度共同决定了城市空间形态的内外空间分配,一定区域内均衡内外部空间能够提高城市空间运作效率,在开发过程中对公共空间的疏密设计和更新策略制定,需要借助公共空间密度指标的定量分析来增加实施方案的科学性,具体指标计算公式如下: 城市交通是作为城市规划结构的骨架,通过交通路线、交通站点能够实现点线结合贯穿纵横,是城市其他功能协调发展的基础[7]。对于城市空间形态的影响主要表现在地面道路上,因此本文将交通模型的评价因子设定为道路等级、道路曲折度和道路密度3个方面。 2.3.1 道路等级 道路等级反映了城市中心区道路疏散的流通能力,一般有主干道、次干道和支路,在对空间形态进行整体的评价时,本文采取道路等级的平均值法,以评价方格网范围内道路的平均宽度作为道路等级的评价数据来源,其计算公式如下: 2.3.2 道路曲折度 道路曲折度与街巷曲折度反映的实际意义相同,但是道路往往和街巷互相衔接,在彼此的数据上具有共性,因此道路曲折度也可以用道路直线距离和道路长度来表示,其计算公式如下: 其中,T1为道路曲折度;l1为道路端点直线距离;L1为道路总长度。 2.3.3 道路密度 道路密度反映了在既定的城市中心区域内,城市道路占总区域面积的比例,用道路密度作为交通模型的评价因子能够清晰地获得道路和城市的关系[8],以此来作为中心区道路设计和区域疏散之间的关系求证,方便道路和建筑组团之间的关系确定,其计算公式如下: 本文将借助综合模糊评价法建立空间形态影响因素的评价方法,主要是通过建立一级因子和二级因子之间的评价指标矩阵和隶属度子集,见表1所列,以二级指标的权重获得来决定一级指标的权重,在已知权重的基础上,以GIS网格的不同范围作为相应的函数关系,用图像来获得标准指标和现状指标之间的差异。 表1 老中心区空间形态影响因素模糊评价的隶属度矩阵 表1中的动态指标系数是依据不同的城市发展状况确定的,舒适指标权重是通过在1 000 m2的城市老中心区中发放有关对建筑环境、公共空间环境、道路状况满意度的调查问卷中获得的,最终统计得到这三者相对应满意度比为2∶3∶5,这说明对建筑环境的满意度最低,也表明相应的舒适指标要提高,因此三者的舒适指标为: h=[0.5,0.3,0.2] 其中,一级指标权重的计算如下: 其中0<[I1,I2,I3]<1,将最终I值与不同面积的GIS图像方格网作为2个变量建立函数关系,并与h值进行比较,测定城市老中心区空间形态在不同面积中的各因素变化控制状况。本文以杭州上城区为案例,在调研所获得的数据基础上按照上述方法进行验证。首先建立杭州上城区城市空间图像的GIS图像网格,具体如图1所示。在图1建立的方格坐标中,按照从小到大的范围进行数据递增变化,由于街道和建筑分布状况不同,因此每个网格内的具体数据需分别计算。截止2016年底,本文得到整个上城区恒定的总体数据见表2所列。 图1 杭州上城区网格坐标 表2 上城区总体建设面积数据统计 km2 考虑到上城区是杭州市的老城中心区,有很多历史地段的保护条例限制,因此整个城区的空间形态波动不大,本文根据文献[9]确定的二级指标权重的标度值,动态系数的确定则根据城区发展而综合评定,其中 选取网格包含范围大小,并将数据分别带入(11)~(13)式进行计算,从而得到杭州上城区建筑模型指标、公共空间模型指标和交通模型指标的函数图像,如图2~图4所示。 从图2可以看出,随着网格面积的增大建筑模型指标也逐渐增大,网格面积在6 400 m2时建筑模型达到空间形态的最佳舒适指标,从而确定最佳二级因子的数值。 从图3可以看出,公共空间模型的指标在某个范围内波动,在不同网格面积的参照中有多次接近最佳值,说明公共空间模型对空间形态的影响是基于网格面积的动态数值,可以依据不同的范围确定相应的二级因子数值。 从图4可以看出,交通模型的指标数值在不同的网格区域内围绕最佳值上下波动,这说明杭州上城区交通模型对空间形态的影响总体上趋于最佳。 图2 杭州上城区建筑模型指标函数图像 图3 杭州上城区公共空间模型指标函数图像 图4 杭州上城区交通模型指标函数图像 本文基于对城市老中心区空间形态控制要素的具体分析,得出以下结论: (1) 建筑模型、公共空间模型和交通模型可以依据相对应的二级控制因子建立数值矩阵,进而可用现状数据来获得对城市空间形态进行评价分析。 (2) 通过综合模糊评价矩阵的建立,能够建立标准值和参照值之间的函数关系,并能够在各个指标计算和函数关系中清晰反映各自的影响程度。 (3) 通过杭州上城区的具体实例研究发现,建筑模型对城市空间的影响最佳值对应一个方格网面积,能够按照这个方格网对应的数值确定具体的S0、h0、ρ0的值。同样能够根据公共空间模型和交通模型的函数关系图像确定具体的P0、P1、ρ1、T0、T1、ρ2值。 (4) 公共空间模型和交通模型的评价值是动态的,说明在不同网格内公共空间和交通的二级因子对应数值不是恒定的,但在偏离最佳值的区间内能够根据最近最佳值对应的数值进行调整。 [1] 史宜,杨俊宴.回首百年:城市空间形态研究的谱系建构[J].城市规划,2015,39(12): 9-18. [2] GEOFFREY C,MPHAMED H.THOMAS Isabelle.Measuring urban forms from inter-building distances: Combining MST graphs with a Local Index of Spatial Association[J].Landscape and Urban Planning,2017,163(7):80-89. [3] 赵景柱,宋瑜,石龙宇,等.城市空间形态紧凑度模型构建方法研究[J].生态学报,2011,31(21):6338-6343. [4] 刁星,程文.城市空间绩效评价指标体系构建及实践[J].规划师,2015(8):110-115. [5] 杨俊宴,钱舒皓.特大城市中心体系空间肌理分异研究:以重庆市为例[J].城市规划学刊,2014(4):18-23. [6] VANDERHAEGEN S,CANTERS F.Mapping urban form and function at city block level using spatial metrics[J].Landscape and Urban Planning,2017,167(11):399-409. [7] 黄晶,贾新锋,李勋.基于综合量化分析的城市街区空间公共化改造:以郑州主城区一般城市街区为例[J].规划师,2017(8):85-91. [9] 陈勇.城市空间评价方法初探:以重庆南开步行商业街为例[J].规划师,1997(4):38-45. Researchonevaluationtheoryandmethodoffactorsinfluencingspatialforminoldurbancentralarea WANG Liang1,2, WANG Yanhui2 (1.School of Architecture Engineering, Nanjing Institute of Technology, Nanjing 211167, China; 2.Research Institute of Architecture, Southeast University, Nanjing 210096, China) Based on the analysis of the main factors influencing the spatial form in old urban central area, the corresponding first-level evaluation index and second-level evaluation index are established, and the weight determination of the building model, public space model and traffic model in old urban central area is conducted by using comprehensive fuzzy evaluation method. The function relation between the weight and the changes of area mesh is established, and the actual value is compared with the best comfort value of each first-level index in the function graph, and then the best spatial form in a certain area of the city can be found out. Finally, taking the Shangcheng District in Hangzhou City as an example, the scientificity of the proposed evaluation method is validated, hoping to provide a basis for making decisions about urban planning and management. old urban central area; spatial form; influence factor; comprehensive fuzzy evaluation; function relation 2017-09-18; 2017-10-18 国家自然科学基金资助项目(51578124);教育部人文社会科学研究青年基金项目资助(15YJCZH158) 汪 亮(1980-),男,安徽枞阳人,博士,南京工程学院副教授; 王彦辉(1972-),男,河北石家庄人,博士,东南大学教授,博士生导师. 10.3969/j.issn.1003-5060.2017.12.024 TU984 A 1003-5060(2017)12-1709-03 (责任编辑万伦来)2 空间形态影响因素的评价内容
2.1 建筑模型的评价

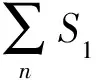
2.2 公共空间模型评价
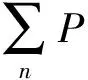
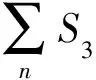
2.3 交通模型评价
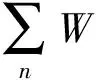
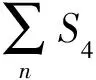
3 空间形态影响因素的评价方法

5 结 论
