例析高考数学试题与教材例习题之间的“变度”

王员员 李忠如

[摘  要] 随着高考改革的深化，高考命题增强了基础性和综合性的考查. 本文以2017年高考全国Ⅱ卷文科试卷的客观题为例，对注重基础性作了另类解析，由此建议高考复习要注重基础，寻找方法;注重变式，提升能力.

[关键词] 高考;教材;基础性

2014年9月公布的《国务院关于深化考试招生制度改革的实施意见》（以下简称为《意见》）明确提到，2015年起增加使用全国统一命题试卷的省份. 据统计，2017年全国有25个省份高考数学回归全国卷，这必将引起全国各地高中数学教师和学生的重点关注.

2017年高考命题贯彻《意见》的要求，以必备知识、关键能力、学科素养、核心价值为考查内容，以基础性、综合性、应用性、创新性为考查要求[1]. 那么，由2017年高考数学命题如何突出“基础性”的考查，对高中数学教师的日常教学有什么启示？众所周知，高中数学课程标准是高中数学教科书（以下简称为“教材”）编写的依据，而教材又是教师教学的重要参考、学生学习的重要素材. 仔细分析发现，2017年高考数学试卷中有不少的考题都是教材中的例习题改编而成，要么是简单变化，要么是简单改造，要么是多个题的重组，也就是说可以在教材中找到原型题目. 本文以2017年高考全国Ⅱ卷文科试卷中16道客观题（这里指选择题和填空题）为例，对注重基础性作了另类解析，即分析了高考数学试题与教材例习题之间的“变度”（即改变程度），以帮助一线教师和高中学生进一步明确教材是“本”的认识.

改编的第一层次——换数字

换数字是教材中例习题改编为高考题的最低层次，往往针对最基础的概念、最基本的技能的考查，无论是编题的难度还是答题的难度都很低，学生一般只是需要简单的套用所学知识就可以求解，但是这种改编方式在高考题中也频频出现（见表1）.

高考真题1：（2017年高考全国Ⅱ卷文科第1题）设集合A={1，2，3}，B={2，3，4}，则A∪B=（  ）

A. {1，2，3，4}？摇 B. {1，2，3}

C. {2，3，4}？摇？摇 D. {1，3，4}

教材原题：设A={4，5，6，8}，B={3，5，7，8}，求A∪B.

该高考题只不过是将教材原题中集合A，B的元素改变，考查集合的并集的求法. 這种改编方式往往出现在考查集合、复数的运算，函数的单调区间、最值等容易题目，无论换成什么数字，都只是考查相关的概念或者运算，这就只要求学生理解基本概念，掌握基本运算.

改编的第二层次——改形式

改形式是较换数字略为复杂的一种改编方式，除了简单换数字以外，还会改变情境或者图形等，使得题目的呈现形式改变. 这种题目就需要学生跳出题目的情境或图形，识别其本质，从而找到解题方法，这种改编方式在高考题中也并不鲜见（见表2）.

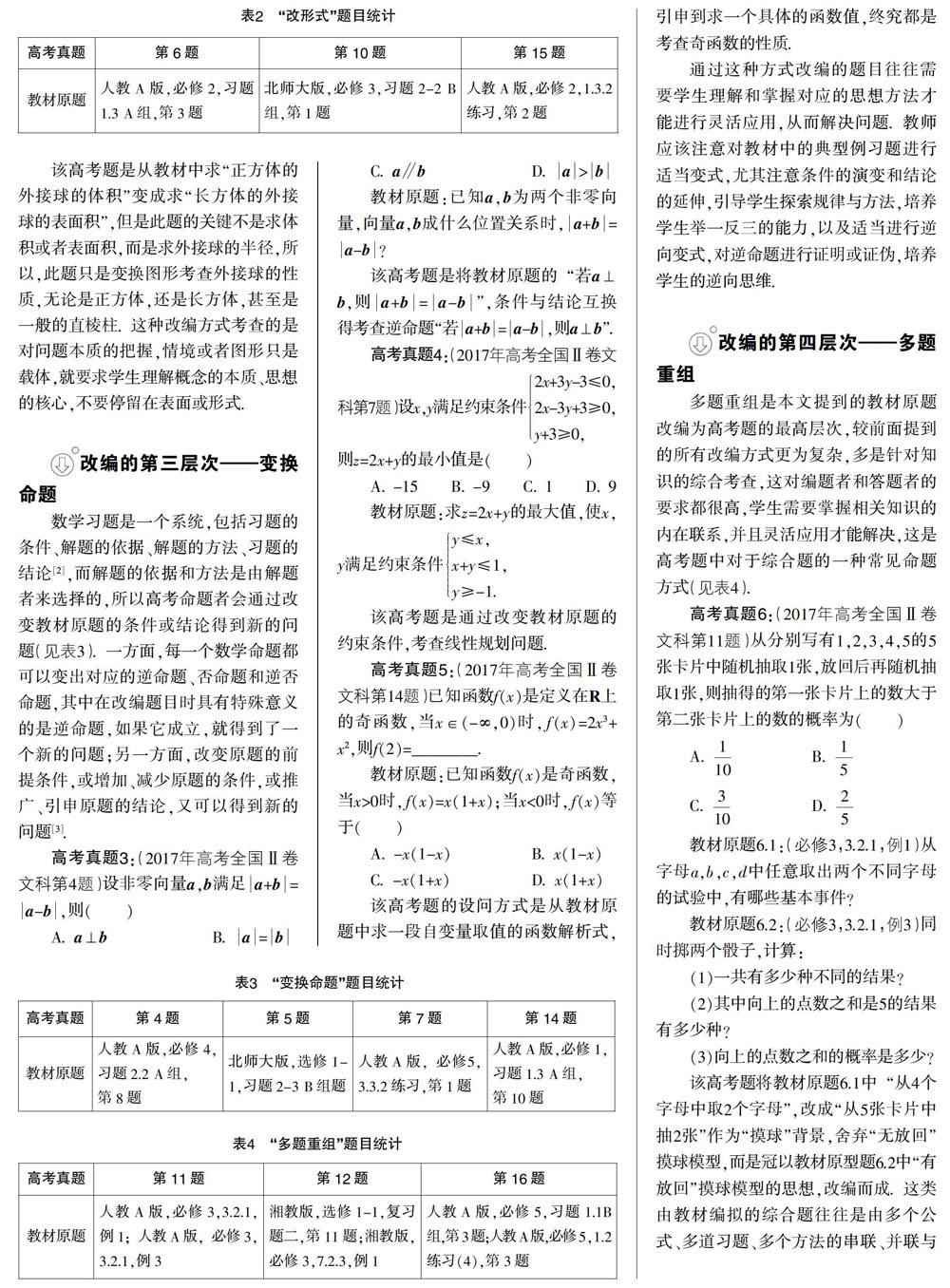
高考真题2：（2017年高考全国Ⅱ卷文科第15题）长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，则球O的表面积为__________.

教材原题：一个正方体的顶点都在球面上，它的棱长是a cm，求球的体积.

该高考题是从教材中求“正方体的外接球的体积”变成求“长方体的外接球的表面积”，但是此题的关键不是求体积或者表面积，而是求外接球的半径，所以，此题只是变换图形考查外接球的性质，无论是正方体，还是长方体，甚至是一般的直棱柱. 这种改编方式考查的是对问题本质的把握，情境或者图形只是载体，就要求学生理解概念的本质、思想的核心，不要停留在表面或形式.

改编的第三层次——变换命题

数学习题是一个系统，包括习题的条件、解题的依据、解题的方法、习题的结论[2]，而解题的依据和方法是由解题者来选择的，所以高考命题者会通过改变教材原题的条件或结论得到新的问题（见表3）. 一方面，每一个数学命题都可以变出对应的逆命题、否命题和逆否命题，其中在改编题目时具有特殊意义的是逆命题，如果它成立，就得到了一个新的问题;另一方面，改变原题的前提条件，或增加、减少原题的条件，或推广、引申原题的结论，又可以得到新的问题[3].

高考真题3：（2017年高考全国Ⅱ卷文科第4题）设非零向量a，b满足a+b=a-b，则（  ）

A. a⊥b B. a=b

C. a∥b？摇 D. a>b

教材原题：已知a，b为两个非零向量，向量a，b成什么位置关系时，a+b=a-b？

该高考题是将教材原题的“若a⊥b，则a+b=a-b”，条件与结论互换得考查逆命题“若a+b=a-b，则a⊥b”.

高考真题4：（2017年高考全国Ⅱ卷文科第7题）设x，y满足约束条件2x+3y-3≤0，2x-3y+3≥0，y+3≥0，则z=2x+y的最小值是（  ）

A. -15  B. -9  C. 1  D. 9

教材原题：求z=2x+y的最大值，使x，y满足约束条件y≤x，x+y≤1，y≥-1.

该高考题是通过改变教材原题的约束条件，考查线性规划问题.

高考真题5：（2017年高考全国Ⅱ卷文科第14题）已知函数f（x）是定义在R上的奇函数，当x∈（-∞，0）时， f（x）=2x3+x2，则f（2）=________.

教材原题：已知函数f（x）是奇函数，当x>0时， f（x）=x（1+x）;当x<0时， f（x）等于（  ）

A. -x（1-x） B. x（1-x）

C. -x（1+x）？摇？摇 D. x（1+x）

该高考题的设问方式是从教材原题中求一段自变量取值的函数解析式，引申到求一个具体的函数值，终究都是考查奇函数的性质.

通过这种方式改编的题目往往需要学生理解和掌握对应的思想方法才能进行灵活应用，从而解决问题. 教师应该注意对教材中的典型例习题进行适当变式，尤其注意条件的演变和结论的延伸，引导学生探索规律与方法，培养学生举一反三的能力，以及适当进行逆向变式，对逆命题进行证明或证伪，培养学生的逆向思维.

改编的第四层次——多题重组

多题重组是本文提到的教材原题改编为高考题的最高层次，较前面提到的所有改编方式更为复杂，多是针对知识的综合考查，这对编题者和答题者的要求都很高，学生需要掌握相关知识的内在联系，并且灵活应用才能解决，这是高考题中对于综合题的一种常见命题方式（见表4）.

高考真题6：（2017年高考全国Ⅱ卷文科第11题）从分别写有1，2，3，4，5的5张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为（  ）

教材原题6.1：（必修3，3.2.1，例1）从字母a，b，c，d中任意取出两个不同字母的试验中，有哪些基本事件？

教材原题6.2：（必修3，3.2.1，例3）同时掷两个骰子，计算：

（1）一共有多少种不同的结果？

（2）其中向上的点数之和是5的结果有多少种？

（3）向上的点数之和的概率是多少？

该高考题将教材原题6.1中“从4个字母中取2个字母”，改成“从5张卡片中抽2张”作为“摸球”背景，舍弃“无放回”摸球模型，而是冠以教材原型题6.2中“有放回”摸球模型的思想，改编而成. 这类由教材编拟的综合题往往是由多个公式、多道习题、多个方法的串联、并联与综合[4]，但是无论怎样组合，最终都可以分解成几个基本问题进行解决. 比如，高中函数的综合题多是函数与导数、数列、不等式等相关知识的题目进行综合，从而这类问题多是可以分解为对应的几个知识块的基本问题进行解决的. 因此，对于教材中相互关联或者易于混淆的知识，教师应该注意对比强调，并对综合性题目进行分解变式，培养学生解决综合问题的能力.

综上所述，2017年高考全国Ⅱ卷文科试卷的客观题，除了第9题逻辑推理题外，其他题目均可从教材中找到原型题目，即此套高考题的客观题基本上属于教材原题改编，只要学生掌握教材中的基础知识、基本技能和基本思想方法，就能做到客观题基本不失分.

事实上，除了大部分的客观题来源于教材，中、低档的主观题也可以找到教材原型题. 因此，在高中的学习过程中，尤其是高考复习阶段，教师和学生都应该重视教材，合理利用教材. 首先，注重基础. 教材中的大多数例习题都具有较强的基础性，有助于学生对基础的夯实[5]，利用教材可促使学生对基本概念和基本思想的理解和掌握，并熟练掌握一些基本技能[6]. 所以，教师应该帮助学生理解教材中的一些数学概念、公式、定理等基础知识的来龙去脉，掌握教材中的一些运算、作图等基本技能，体会教材中的数形结合、转化等基本思想，从而帮助学生建构知识体系，寻找解题方法. 其次，注重变式. 正如“艺术来源于生活，而高于生活”，高考来源于教材，而高于教材. 所以，教师应该精选例习题，并且通过条件变式、结论变式、逆向变式、图形变式、分解变式、拓广变式[7]等方法进行适当变式，从而帮助学生提高思维能力，提升解题能力.

数学的呈现方式可以是千变万化的，但是数学基础知识、基本技能和基本思想方法是不变的. 高考题来源于教材，却与教材原题有所不同，这就是呈现方式的改变，但是考查的知识、技能和思想方法是不变的. 所以，只有夯实基础，提升能力，才能在高考中以不变应万变.

参考文献：

[1]  教育部考试中心. 围绕高考核心功能 全面深化考试内容改革[N]. 中国教育报，2017-06-09（5）.

[2]  戴再平. 数学习题理论[M]. 上海：上海教育出版社，1991.

[3]  钟善基. 中国著名特级教师教学思想录（中学数学卷）[M]. 南京：江苏教育出版社，1996.

[4]  罗增儒.高考复习要抓住根本[J].中学数学教学参考，2016，（12）.

[5]  徐玲. 高中数学课本例题的研读技巧[J]. 中学数学教学参考，2016，（12）.

[6]  中华人民共和国教育部.普通高中數学课程标准（实验）[S]. 北京：人民教育出版社，2003.

[7]  刘长春，张文娣. 中学数学变式教学与能力培养[M]. 济南：山东教育出版社，2001.