具有不确定性连接刚度的太阳电池阵基频分析

庞梦非，朱春艳，张美艳，唐国安

(1.复旦大学 航空航天系,上海 200433； 2.上海宇航系统工程研究所,上海 201109)

具有不确定性连接刚度的太阳电池阵基频分析

庞梦非1，朱春艳2，张美艳1，唐国安1

(1.复旦大学 航空航天系,上海 200433； 2.上海宇航系统工程研究所,上海 201109)

以铰链副抗弯刚度具不确定性的太阳电池阵为研究对象，考虑加工和实验误差等随机因素，用数值计算方法仿真电池阵的基频实验，对安装在同一电池阵上的不同组、抗弯刚度满足一定分布规律的铰链副进行多次仿真实验，建立了铰链副抗弯刚度和电池阵基频的仿真样本，用高斯过程回归方法训练出两者间的映射关系，获得了电池阵基频期望值及置信区间关于铰链副抗弯刚度的变化关系。给出了电池阵基频关于铰链副刚度参数不确定性的分析流程。分析结果表明：在铰链副刚度不确定条件下，高斯过程回归方法可确定电池阵基频期望值和协方差表达式中的超参数，与其他回归或插值方法等相比，不仅能预示电池阵基频的期望值，而且可估计其置信区间。在加工和实验误差不可避免的实际情况下，有必要生产多组铰链副进行模态实验并对同一组铰链副适当增加重复实验次数，使其能合理预示电池阵基频的不确定性，减小实验误差的影响，预示合理的基频。

太阳电池阵； 铰链副； 仿真实验； 刚度； 固有频率； 不确定性； 高斯过程回归； 置信区间

0 引言

不确定性问题广泛存在于工程结构和装备的装配、制造中，如受加工工艺限制，结构的刚度、质量和阻尼等力学参数总表现出一定的随机性。正确估计参数不确定性对结构力学特性和行为的影响有重要的工程应用价值。模糊方法、区间方法和概率方法是目前不确定性建模的三种主要方法。用模糊集合理论描述不确定性，由此发展出模糊有限元方法。文献[1]用模糊方法对薄壁组合梁进行了不确定性分析。文献[2]求解了具不确定参数的结构动力学分析的模糊特征值求解问题。用基于模糊集理论的方法描述不确定性时，需获知不确定性结构参数的隶属度函数。多数情况下，确定隶属度函数非常困难，使用者常不得不主观性地选取相应的隶属度函数。这样的分析结果可靠性并无保障。区间分析方法是在信息不充分条件下，描述工程问题不确定性的一种方法，将这些不确定性结构参数视为未知变量在具已知边界的区间内取值。文献[3]较早将区间分析法引入工程结构中不确定性问题的研究。文献[4-5]用区间有限元方法计算了不确定系统的频响函数包络，提出了不确定结构频响函数包络分析的区间灵敏度理论。文献[6]综合了区间分析法与有限元方法，求解传递函数的包络。区间分析方法无需事先获知不确定参数的很多信息，只需知道不确定参数的上下限。对直接采用区间数学运算法则求解线性区间方程组的方法进行了研究，但该法难以用于求解大规模问题，更重要的是其预测的范围大于实际值，结果过于保守。文献[7-9]最先引入贝叶斯概率框架估计不确定性结构模型参数，贝叶斯概率框架在解决模型修正过程中不确定性的效果显著，但由于计算量过大，在工程实际中的应用受限。文献[10]综合了摄动和有限元法，研究了一般概率摄动有限元方法，并用随机摄动法分析了有不确定参数和不确定载荷的振动机械系统响应[11]。文献[12]用摄动有限元法对不确定结构静动态特性的稳健优化设计进行了研究。高斯过程回归方法建立在贝叶斯概率理论的基础上，在机器学习等领域中发挥了重要作用，但目前用其解决工程中不确定性问题的研究较少。本文将采用高斯过程回归方法，探讨其在解决工程不确定性问题中的适用性。

本文以铰链副抗弯刚度具不确定性的太阳电池阵为研究对象，用数值计算方法仿真电池阵的基频实验，考虑加工和实验误差等随机因素，对安装在同一电池阵上的不同组、抗弯刚度满足一定分布规律的铰链副进行多次仿真实验，建立铰链副抗弯刚度和电池阵基频的仿真样本，通过高斯过程回归方法训练两者间的映射关系。在此基础上，希望得到电池阵基频期望值及置信区间关于铰链副抗弯刚度的变化关系，使给定一个抗弯刚度实验值就能预测出电池阵基频的期望值，并对方差作出估计。

1 单输出高斯过程回归基本原理

高斯过程回归问题可描述为：记x1,…,xn∈Rd为n个输入向量；X=[x1…xn]∈Rd×n为输入矩阵；y1,…,yn∈R1为n个输出标量；y=[y1…yn]T∈Rn为输出向量。此处：Rd，Rd×n分别为d维和d×n维线性空间。再令D={X,y}为已存在的训练样本集，高斯过程回归的基本任务是：根据样本集D，学习输入X与输出y间的映射关系f(x):Rd→R1，使对新的输入向量x*∈Rd能预测出对应的映射值f(x*)∈R1。

对单输出高斯回归问题，考虑以下模型

yi=f(xi)+εi

式中：f(xi)为当输入为xi时对应的随机变量；εi为满足N(0,(σn)2)的独立同分布的噪声；yi为f(xi)受到噪声污染后的观察值；i=1，2，…，n[13]。此处:N(0,(σn)2)表示均值为0、方差为(σn)2的高斯分布。

因高斯过程的任意有限维分布均满足高斯分布，故可得观察值y的先验分布为

y～N(0,C)

(1)

即y满足均值为0、方差为C的高斯分布[14]。此处：C=K(X,X)+(σn)2In；K(X,X)∈Rn×n为对称正定协方差矩阵。

观察值y与预测值f*=f(x*)的联合先验分布为

(2)

式中：K(X,x*)∈Rn×1为预测点x*与训练样本集的输入X间的n×1阶协方差矩阵；K(x*,X)=(K(X,x*))T；k(x*,x*)为预测点x*自身的协方差。

由式(2)可得预测值f*的后验分布为

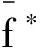
(3)

式中：

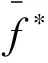
(4)

cov(f*)=k(x*,x*)-K(x*,X)·

C-1K(X,x*)

(5)

则可得以概率形式表示的预测结果。

高斯过程的性质取决于其均值函数和协方差函数。常用的协方差函数有平方指数协方差函数、Matern类协方差函数和神经网络协方差函数。平方指数协方差的形式为

k(xp,xq)=

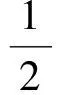
(6)

式中：xp，xq为任意两个d维向量；(σf)2=covf为随机变量f的方差，表示随机变量偏离期望值的程度。若令M=λ-2I，则式(6)可简化为

(7)

式中：λ为输入量的特征距离。协方差中的未知数σf，λ被称为超参数。单输出高斯过程回归方法中的超参数还包括噪声的标准差σn。令θ为预测模型中所有超参数组成的向量，对式(7)表示的协方差函数，θ=[λ(σf)2(σn)2]，一般可用极大似然法估计超参数的初始值[14]。同时，根据概率论中的贝叶斯原理，可得超参数的概率表达形式并将问题转换为对其极大值的求解，有

(8)

设θ接近于均匀分布，即概率密度p(θ)可近似为常量，则寻找函数p(θ|y,X)的最大值等价于寻找p(y|X,θ)的最大值问题

(9)

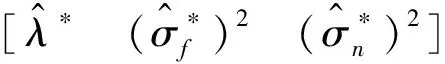
优化设计理论证明了梯度下降法速度较快的优点，但其缺点是易陷入局部极值点。为此，文献[15]提出了一种超参数初始值的优化方法。本文采取了该优化方法，可得到较好的结果。

2 电池阵基频关于铰链副刚度参数不确定性分析

航天器上使用的电池阵很多是由若干太阳电池板通过压紧-锁定的铰链副连接的，航天器姿态控制律设计等需要电池阵的基频数据。铰链副是一种机构，因加工、装配等各种因素的差异，对电池阵整体结构提供的连接刚度存在相当大的不确定性。基频的实验测试结果也必定存在随机性，最终得到的基频数据必具有不确定性。基于已有的铰链副刚度参数和电池阵基频实测结果，预示一个给定铰链副刚度实验值下的电池阵基频并估计其不确定性有重要的工程应用价值。

2.1 太阳电池阵模型及其不确定性分析过程

为说明基频及其不确定性预示的过程和结果，本文用数值计算方法仿真电池阵的基频实验。电池阵的基频实验如图1(a)所示。实验时用有机玻璃板替代实际的电池板，局部放大的是连接两块电池板的铰链副[16]。仿真所用电池板的有限元模型如图1(b)所示，模型中铰链副等效为梁单元。在此状态下，基频对应的模态是垂直于XY平面的弯曲。有机玻璃板及等效梁模型的属性参考了文献[17]。

电池阵基频关于铰链副刚度参数的不确定性分析流程为：

a)设置多组铰链副刚度系数，构造输入矩阵X；

b)电池阵基频测试实验仿真，获得输出向量y；

e)预示给定铰链副刚度实验值下的电池阵基频并估计其不确定性。

2.2 高斯过程回归方法分析结果

仅讨论单输入情形，连接有机玻璃板的一对铰链副具有相同的刚度。基频对应的模态主要受到绕y轴的抗弯刚度的影响，将铰链副等效为梁单元后即为绕y轴的抗弯刚度EI，文献[17]用实验方法辨识得到EI=316 N·m2。由于加工和装配工差等因素，即使是同一生产批次的不同铰链副，其抗弯刚度也存在差异。这种差异具随机性，根据加工误差统计特性可认为其服从正态分布。为模拟此情形，将文献[17]的实测结果EI≈316 N·m2作为期望值，取标准差为60 N·m2，正态分布的三个抗弯刚度作为对三个铰链副进行仿真实验，由得到的抗弯刚度值可构造出输入矩阵

对上述三个铰链副的抗弯刚度样本分别进行基频实验。仿真时用有限元计算程序依次计算出铰链副刚度分别为X中各分量时对应的电池阵基频，即基频分别为

f= [f1f2f3]=

[9.139 5 9.677 5 9.878 9] Hz

为模拟实验过程存在的各种误差，将f中的每个元素叠加服从高斯分布的随机向量ε～N(0,0.12)，作为由仿真实验得到的输出样本

y= [y1y2y3]=

[9.249 5 9.832 0 9.887 4] Hz

图2中：蓝线即为高斯过程回归模型的训练结果；绿线为理论曲线；红线包围的部分为99%置信区间，说明将一个已测得刚度参数的铰链副安装在电池阵上进行模态实验，电池阵的基频有99%的可能性处于红色线范围内。由图2可知：所得结果曲线受采样点影响很大，与理论曲线趋势相差较大，却给出了很小的置信区间，这与实际情况不符。

为避免实验误差导致的不合理预测结果，用相同方法构造出输入矩阵

X=[EI1EI2EI3]=

[346.648 5 276.623 6 308.499 0] N·m2

获得铰链副抗弯刚度值后进行基频仿真实验，每个抗弯刚度样本分别进行基频实验5次。仿真时，用有限元计算程序依次计算铰链副刚度分别为X中各分量时对应的电池阵基频，所得基频分别为

f= [f1f2f3]=

[9.863 4 9.366 6 9.611 3] Hz

同样，为模拟实验过程存在的各种误差，对f中的每个元素叠加服从高斯分布的随机向量ε～N(0,0.12)，每个点实验5次即叠加5次。记由仿真实验得到的输出样本为y=[y1…y15]。此处：y1=9.810 4 Hz；y2=9.874 0 Hz；y3=9.976 3 Hz；y4=9.937 7 Hz；y5=9.977 8 Hz;y6=9.275 1 Hz；y7=9.384 6 Hz；y8=9.268 3 Hz；y9=9.405 1 Hz；y10=9.399 2 Hz；y11=9.740 9 Hz；y12=9.721 2 Hz；y13=9.676 6 Hz；y14=9.560 8 Hz；y15=9.563 7 Hz。其中y1～y5，y6～y10，y11～y15分别对应同一个抗弯刚度值。

不同抗弯刚度下两块有机玻璃板和一对铰链副组成的电池阵的基频如图3所示。

由图3可知：计算曲线与理论曲线非常接近，预测效果较好；模型还能给出样本点输出的置信区间。图3中叠加了计算曲线的99%置信区间(红色线包围部分)。本文研究结果表明：对此单输出高斯过程回归问题，若每个抗弯刚度值对应只进行1次基频实验，则实验误差可能会导致结果曲线与理论曲线偏差较大。经过多次的仿真和计算，发现在同一个抗弯刚度值下进行5次实验就可获得较好的预测效果。

3 结束语

本文对具不确定性连接刚度的太阳电池阵基频仿真分析方法进行了研究。高斯过程回归方法能通过少量的样本点训练出大量的预测值，将其用于工程实际问题的不确定性分析，可减少试验工况。基于太阳电池阵模态实验的仿真结果表明：在铰链副刚度不确定条件下，高斯过程回归方法可确定电池阵基频期望值和协方差表达式中的超参数，与其他回归或插值方法等相比，不仅能预示电池阵基频的期望值，并且能估计其置信区间。分析结果表明：太阳电池阵的同一铰链副必须进行多次模态实验，才能减少实验误差造成的影响、预示出合理的基频结果。对真实的模态实验，应用高斯过程回归方法预示太阳电池阵基频有待进一步研究。如实际情况中，同一电池阵中不同铰链副的刚度存在差异，要求预示的频率不仅限于基频，这些多输入多输出问题也需拓展。

[1] PAWAR P M, NAM JUNG S, RONGE B P. Fuzzy approach for uncertainty analysis of thin walled composite beams[J]. Aircraft Engineering and Aerospace Technology, 2012, 84(1): 13-22.

[2] XIA Y, FRISWELL M. Efficient solution of the fuzzy eigenvalue problem in structural dynamics[J]. Engineering Computations, 2014, 31(5): 864-878.

[3] RAO S S, BERKE L. Analysis of uncertain structural systems using interval analysis[J]. AIAA Journal, 1997, 35(4): 727-735.

[4] MOENS D, VANDEPITTE D. An interval finite element approach for the calculation of envelope frequency response functions[J]. International Journal for Numerical Methods in Engineering, 2004, 61(14): 2480-2507.

[5] MOENS D, VANDEPITTE D. Interval sensitivity theory and its application to frequency response envelope analysis of uncertain structures[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(21): 2486-2496.

[6] DESSOMBZ O, THOUVEREZ F, LANÉ J P, et al. Analysis of mechanical systems using interval computations applied to finite element methods[J]. Journal of Sound and Vibration, 2001, 239(5): 949-968.

[7] BECK J L, KATAFYGIOTIS L S. Updating models and their uncertainties I: Bayesian statistical framework[J]. Journal of Engineering Mechanics, 1998, 124(4): 455-461.

[8] KATAFYGIOTIS L S, BECK J L. Updating models and their uncertainties. II: model identifiability[J]. Journal of Engineering Mechanics, 1998, 124(4): 463-467.

[9] KATAFYGIOTIS L S, PAPADIMITRIOU C, LAM H F. A probabilistic approach to structural model updating[J]. Soil Dynamics and Earthquake Engineering, 1998, 17(7): 495-507.

[10] 张义民, 刘巧伶, 闻邦椿. 多自由度非线性随机参数振动系统响应分析的概率摄动有限元法[J]. 计算力学学报, 2003, 20(1): 8-11.

[11] 张义民, 闻邦椿. 非线性随机振动机的动力学研究[J]. 工程力学, 1999, 16(3): 100-104.

[12] 亢战, 程耿东. 非确定性结构静动态特性稳健优化设计[J]. 力学学报, 2006, 23(1): 57-65.

[13] RASMUSSEN C E, WILLIAMS C K I. Gaussian process for machine learning[M]. Cambridge: MIT Press, 2006: 8-24.

[14] 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 北京: 高等教育出版社, 2008: 14-20+46+152-156.

[15] 单志辉. 基于高斯过程回归的翼型快速设计研究[D]. 南京: 南京航空航天大学, 2011.

[16] 马越峰, 江礼俐, 苏里, 等. 太阳电池阵的铰链副刚度参数识别[J]. 上海航天, 2006, 23(3): 23-27.

[17] 马越峰. 振动结构的参数识别与模型修正及其应用[D]. 上海: 复旦大学, 2005.

[18] MAGRAB E B. An engineer's guide to MATLAB: with applications from mechanical, aerospace, electrical, civil, and biological systems engineering[M]. Englewood Cliffs: Prentice Hall, 2011: 710-712.

FundamentalFrequencyAnalysisofSolarCellArraywithUncertainConnectionStiffness

PANG Meng-fei1， ZHU Chun-yan2， ZHANG Mei-yan1， TANG Guo-an1

(1. Department of Aeronautics and Astronautics, Fudan University, Shanghai 200433, China;2. Aerospace System Engineering Shanghai, Shanghai 201109, China)

With the consideration of the random factors such as machining and experimental error, solar cell array with a hinge pair which had uncertain bending stiffness was taken as an example and the fundamental frequency test was simulated by numerical method in this paper. The different hinge pairs and their bending stiffness satisfying certain distribution law which were amounted on the same solar cell were simulated many times. The simulation model of the hinge pair bending stiffness and the cell array fundamental frequency were established. The mapping between them was trained by the Gaussian process regression method. On this basis, the relationship between the expected value and confidence interval of the cell array fundamental frequency and the hinge pair bending stiffness was obtained. The uncertainty analysis process of cell array fundamental frequency with the respect to the stiffness parameters of hinge pair was given. The results show that the fundamental frequency expected value of the cell and super parameters in the covariance expression can be determined by the Gaussian process regression methods under the condition of uncertainty of hinge pair stiffness. It can not only indicate the expected value of the fundamental frequency but also estimate its confidence interval, which is different from other regression method or interpolating method. In order to reasonably predict the uncertainty of the cell array fundamental frequency, it is necessary to produce multiple sets of hinge pairs to do modal experiments and to increase the number of repetitive experiments on the same hinge pair in the actual case where the processing and experimental errors are inevitable.

solar cell array; hinge pair; simulation; stiffness; natural frequency; uncertainty; Gaussian process regression; confidence interval

1006-1630(2017)06-0103-06

V414.33

A

10.19328/j.cnki.1006-1630.2017.06.016

2017-05-20；

2017-07-12

国家自然科学基金项目资助(11572089)；上海市科学技术委员会扬帆计划项目资助(15YF1411900)

庞梦非(1993—)，女，硕士生，主要研究方向为结构动力学。

唐国安(1962—)，男，教授，主要研究方向为结构动力学。