基于最大似然准则的L阵2D-DOA配对算法研究

王志诚，徐 卉，郭晓江，高叶盛

(1.上海无线电设备研究所,上海 200090； 2.上海交通大学 电子信息与电气工程学院,上海 200240)

基于最大似然准则的L阵2D-DOA配对算法研究

王志诚1，徐 卉1，郭晓江2，高叶盛2

(1.上海无线电设备研究所,上海 200090； 2.上海交通大学 电子信息与电气工程学院,上海 200240)

针对L阵两维到达方向(2D-DOA)估计中方位角和俯仰角配对错误导致的模糊问题，对一种基于最大似然准则的配对算法进行了研究。根据建立的L阵信号模型，用超分辨算法获得在非相干源和相干源时的L阵两组线阵的一维DOA估计。由一个线阵接收数据和估计的一维DOA得出信源的最大似然估计，构造第一个信源协方差矩阵，其中目标的排列顺序与该线阵估计的一维DOA顺序对应；再用两个线阵接收数据的互相关矩阵估计第二个信源协方差矩阵。当两个线阵估得的一维DOA对应时两个信源协方差矩阵等价，可由两个矩阵中元素的位置关系实现配对，获得无模糊的方位角和俯仰角。仿真结果表明：所提算法在低信噪比、小快拍数下均具较高的鲁棒性，适用范围广，在无任何先验信息条件下能较准确地实现配对。

2D-DOA估计； 参数配对； 最大似然； 解模糊； L阵； 协方差； 运算量； 鲁棒性

0 引言

根据L阵的阵列结构特征，工程中通常将L阵的2D-DOA估计问题分解为两组一维DOA估计，再通过对这两组一维DOAs配对得到无模糊的方位角和俯仰角。目前，在无任何先验信息时，方位角和俯仰角的配对方法主要有三类。一是对由声学矢量传感器构成的阵列，可直接利用传感器的空间矢量特性实现自动配对，如文献[1-2]，但该法受传感器类型限制而适用范围有限。二是将两个一维DOA估计与配对过程融合，文献[3-4]通过一个含两组一维DOA对应关系的广义协方差矩阵实现DOA估计和自动配对，该法由于协方差矩阵维数较大导致特征分解运算量变大，且相干源条件下协方差矩阵不适于空间平滑等算法解相干；文献[5-6]通过构造两个线阵接收数据的互相关矩阵，并根据该矩阵中两组一维DOA的对应关系得出无模糊的方位角和俯仰角，两种方法同样仅在独立源时有效；文献[7-8]以求解两组一维DOA余弦的差值媒介实现匹配，但当存在相干源时算法同样失效，且仅适于均匀L阵。三是先进行两组一维DOA估计，再独立配对，文献[9-10]通过Toeplitz法估得波与两个线阵一维DOA的余弦差值，以该差值和两组一维DOAs的关系实现配对，该法对相干源同样有效，但两个线阵必须是均匀线阵，且由于Toeplitz法精度较差导致算法鲁棒性较低；文献[11-12]通过信号子空间与噪声子空间渐近正交特性的穷尽搜索配对，在独立源时配对成功率高，但也不适于相干源；文献[13]将由稀疏分解得到信号的幅值信息作为配对的依据，但实际工程中幅值信息有时并不可靠；文献[14]先由所估计的两组一维DOA得出一个“信源协方差矩阵”，再以该矩阵是否为Hermite矩阵为准则判断是否配对正确，但在等强度独立信源情况下算法鲁棒性稍差。

在白噪声背景中，本文对一种通用的适合独立源和相干源的L阵配对算法进行了研究，所提算法属于上述方法中的第三类。先用其中一个线阵接收数据得出信源的最大似然估计，构造出第一个信源协方差矩阵，该协方差矩阵中目标的排列顺序与该线阵估计的一维DOAs顺序对应，再用两个线阵接收数据的互相关矩阵估计第二个信源协方差矩阵，当两个线阵估得的一维DOAs对应时两个协方差矩阵等价，最后根据这个等价关系通过优化实现配对，获得无模糊的方位角和俯仰角。该算法的特点是具较高的鲁棒性，适用范围广，在无任何先验信息情况下仍能较准确地实现配对。

1 L阵信号模型与一维DOA估计

1.1 信号模型

令L阵由两个互相垂直的线阵构成，如图1所示。设两线阵X、Y相交于原点，阵元数分别为M+1，N+1，总阵元数为M+N+1。设有K个同中心频率的远场窄带信号被该L阵接收；λ为载频波长，θk，φk分别为第k个来波信号的方位角和俯仰角(θ∈[0,2π],φ∈[0,π/2],k=1,2,…,K)，假设信源在两个线阵上是可分的，此时L阵的2D-DOA估计问题可分解为两个一维DOA估计。

记ax，ay分别为线阵X、Y的导向矢量；xm为X中第m个阵元至原点的距离(m=1，2，…，M)；yn为Y中第n个阵元至原点的距离(n=1，2，…，N)，则信源k的导向矢量可表示为

(1)

式中：

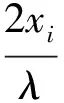
此处：cosαk=cosθkcosφk；cosβk=sinθkcosφk；i=1，2，…，M；j=1，2，…，N；k=1，2，…，K。记Ax，Ay分别为线阵X、Y的阵列流型，且

Ax(α)=[ax(α1)ax(α2) …ax(αK)]

Ay(β)=[ay(β1)ay(β2) …ay(βK)]

sk为第k个信源的复包络，则回波信号可表示为

s(t)=[s1(t)s2(t) …sK(t)]T

记nx，ny为高斯白噪声，则阵列X、Y的接收数据分别为

(2)

1.2 两组一维DOA估计

1.2.1 非相干源

Rxy=E(X(Y′)H)=AxRs(A′y)H

(3)

式中：Rs为信源协方差矩阵。对Rxy作奇异值分解

Rxy=UDVH

(4)

1.2.2 相干源

关于非均匀线阵的快速有效解相干算法的研究相对较少，本文重点是配对算法，因此相干源情况下的预处理以均匀L阵为例。

先对式(3)互相关矩阵进行前向平滑处理

(5)

(6)

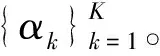
2 基于最大似然准则的配对算法

(7)

根据cosαk,cosβk的正负确定θk在四个象限的位置，调整θk大小。

2.1 配对原理

针对方位角和俯仰角的配对问题，本文提出基于使用源方差矩阵的最大似然法的参数配对法(PMLS算法)。

由文献[10]可知：在高斯白噪声背景中信源阵列流型和复包络的最大似然估计可转为最小二乘问题

(8)

式中：L为快拍数；Yi，si分别为Y，s的第i次采样。显然，si的最小二乘解为

(9)

(10)

(11)

式中：上标“*”表示共轭。将式(10)代入式(11)，得

(12)

式中：Ryy为线阵Y接收数据的协方差矩阵，且

Ryy=E(YYH)=Ay·E(ssH)·(Ay)H+σ2I=

AyRs(Ay)H+σ2I

(13)

式中：σ2为方差；I为单位阵。将式(13)代入式(12)，得

(14)

(15)

(16)

(17)

(18)

(19)

2.2 优化过程

本文通过一个K×K维置换矩阵T优化式(19)的过程，若Tij为矩阵T的第i行j列元素，则

(20)

(21)

若忽略噪声影响，由式(15)、(21)可得

(22)

本文根据T的特殊结构，提出一种简单有效的求解方法。令

(23)

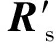
(24)

优化式(24)可得

(25)

易知Ti的解为e1=[1 0 … 0]，e2=[0 1 … 0]，…，eK=[0 0 … 1]中的一个，且T每行的解各异，因此只需计算K+(K-1)+…+3+2=(K-1)(K+2)/2次式(30)，即可得出T，且每次式(25)的计算量小于式(23)。

2.3 配对算法步骤

b)分别用式(12)、(21)估计本文的两个信源协方差矩阵；

c)优化式(23)或式(25)，得出配对置换矩阵T；

3 仿真

本文设计了4个仿真实验，其中：仿真1、2分别验证独立源和相干源时本文算法在不同信噪比下的性能；仿真3验证算法性能在固定低信噪比下随快拍数的变化；仿真4验证算法在多目标时的配对性能。

设仿真条件为：线阵阵元数M=N=10；阵元间距dx=dy=λ/2；高斯白噪声背景，来波与两个线阵的一维DOA估计采用LS-ESPRIT算法，仿真均为500次，仿真1～3均为入射方向为(30°,40°),(50°,45°)的两等强度信号源。其中：CCM法指应用互相关矩阵配对的方法(文献[7])，Hermite法指文献[9]提出的以估计的“信号协方差矩阵”是否为Hermite矩阵为判定准则的配对方法。

仿真1：若两入射信号为独立源，快拍数为200，信噪比(SNR)从-10 dB增至10 dB，仿真所得各方法的配对成功率如图2所示。由图2可知：低信噪比时，本文算法及改进算法的鲁棒性高于文献[7，9]，运算量较小的MPMLS法在低信噪性时能略逊于PMLS法。

仿真2：当两入射信号为相干源时，快拍数仍为200，仿真所得各方法的配对成功率如图3所示。由图3可知：仿真结果与独立源时相似，低信噪比时本文算法的鲁棒性依然较高。

仿真3：当信噪比固定为-5 dB，快拍数从10增至200，仿真所得各方法的配对成功率如图4所示。由图4可知：因本文配对算法采用了最大似然准则，在小快拍数下仍有较高的鲁棒性。

仿真4：阵列结构不变，信噪比为10 dB，快拍数为500，4个目标的入射角分别为(30°，48°)、(50°，49°)、(70°，44°)、(85°，30°)，后两个目标为相干源，用本文PMLS算法配对的俯仰-方位图如图5所示。由图5可知：配对后不存在模糊现象，说明了本文算法对多目标情况的实用性。

4 结束语

在分别用两个线阵估计出两组一维DOA的基础上，本文先通过L阵一个线阵的接收数据和所估计的一维DOAs得出一个信源协方差矩阵，再同时用两个线阵接收数据的互相关矩阵和两组一维DOAs获得第二个信源协方差矩阵，两个信源协方差矩阵在两组一维DOAs对应时是等价的，最后用一个置换矩阵结合这两个协方差矩阵，并用优化方法得出一一对应的两组一维DOAs，实现配对去模糊的目的。与前人的配对算法相比，本文算法较好地解决了相干源的配对难题，同时由于利用了最大似然估计，在低信噪比、小快拍数下仍有较高的鲁棒性。但与其他配对算法类似，本文算法也存在配对成功率随目标数增加而下降的缺点，后续将进一步研究。

[1] 黄家才, 石要武, 陶建武. 多径循环平稳信号二维波达方向估计——极化域平滑法[J]. 电子与信息学报, 2007, 29(5): 1110-1114.

[2] PALANISAMY P, KALYANASUNDARAM N, SWETHA P M. Two-dimensional DOA estimation of coherent signals using acoustic vector sensor array[J]. Signal Processing, 2012, 98: 19-28.

[3] GU J F, WEI P. Joint SVD of two cross-correlation matrices to achieve automatic pairing in 2-D angle estimation problems[J]. IEEE Antennas and Wireless Propagation Letters, 2007, 6: 553-556.

[4] CHENG Q, ZHAO Y M, YANG J. Improvement of 2-D DOA estimation based on L-shaped array[C]// 10th International Symposium on Antennas, Propagation & EM Theory (ISAPE), 2012. Xi’an: [s. n.], 2012: 1233-1236.

[5] AL-JAZZAR S O, MCLERNON D C, SMADI M A. SVD-based joint azimuth/elevation estimation with automatic pairing[J]. Signal Processing, 2010, 90: 1669-1675.

[6] GU J F, ZHU W P, SWAMY M N S. Performance analysis of 2-D DOA estimation via L-shaped array[C]// 25th IEEE Canadian Conference on Electrical & Computer Engineering (CCECE), 2012. Montreal: [s. n.], 2012: 1-4.

[7] LIANG J L, LIU D. Joint elevation and azimuth direction finding using L-shaped array[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(6): 2136-2141.

[8] QADIR S G, FAN Y Y. A comment on “joint elevation and azimuth direction finding using L-shaped array”[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(7): 3546-3547.

[9] SHOHEI K, HIROYUKI T, AKIRA S. Pair-matching method for estimating 2-D angle of arrival with a cross-correlation matrix[J]. IEEE Antennas and Wireless Propagation Letters, 2006, 5: 35-39.

[10] GAN L, WEI P. Comments on “pair-matching method for estimating 2-D angle of arrival with a cross-correlation matrix”[J]. IEEE Antennas and Wireless Propagation Letters, 2008, 7: 807.

[11] 陈根华, 陈伯孝, 杨明磊. 分布式相参阵列及其二维高精度方向估计[J]. 电子与信息学报, 2012, 34(11): 2621-2627.

[12] WANG G M, XIN J M, ZHENG N N, et al.. Computationally efficient subspace-based method for two-dimensional direction estimation with L-shaped array[J]. IEEE Trans on SP, 2011, 59(7): 3197-3212.

[13] 李鹏飞, 张旻, 钟子发. 基于空间角稀疏表示的二维DOA估计[J]. 电子与信息学报, 2011, 33(10): 2402-2406.

[14] WANG G M, XIN J M, ZHENG N N. Two-dimentional direction-of-arrival estimation of coherent signals with L-sharped array[C]// 2010 IEEE Sensor Array and Multichannel Signal Processing Workshop. Jerusalem: IEEE, 2010: 261-264.

[15] GU J F, WEI P, TAI H M. 2-D direction-of-arrival estimation of coherent signals using cross-correlation matrix[J]. Signal Processing, 2008, 88: 75-88.

Pair-MatchingResearchBasedonMaximum-LikelihoodCriterionfor2D-DOAEstimationUsingL-ShapedArray

WANG Zhi-cheng1， XU Hui1， GUO Xiao-jiang2， GAO Ye-sheng2

(1. Shanghai Radio Equipment Research Institution, Shanghai 200090, China; 2. School of Electronic, Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

For the ambiguous problem caused by mismatch of the estimated elevation and azimuth angles for L-shaped array, a novel pair-matching method based on maximum-likelihood criterion was studied in this paper. Firstly, the two groups of 1D-DOAs were obtained from the two linear subarrays of the L-shaped array using super resolution methods. The maximum-likelihood estimation of the signal source was gained by the

signals and estimated 1D-DOAs of one line array, which were used to construct the first source covariance matrix whose alignment order was correspond to the order of the estimated 1D-DOAs of this line array. The second source covariance matrix was estimated by the cross-correlation matrix of the received signals of the two line arrays. If two source covariance matrices were equivalent when the two estimated 1D-DOAs of the two line arrays were corresponded, the matching could be realized to gain the pairs of azimuth and pitch without ambiguity by the position relationship among elements in the two matrices. The numerical simulations show that the proposed method provides better robustness under the low SNR and small snapshots, which can realize the pair matching without any priori information.

2D-DOA estimation; pair matching; maximum likelihood; unwrap ambiguity; L-shaped array; covariance matrices; computation; robustness

2016-07-22；

2017-01-22

国防“十三五”预研基金资助

王志诚(1982—)，男，高级工程师，主要研究方向为雷达总体设计及信号处理。

1006-1630(2017)06-0036-06

TN957.52

A

10.19328/j.cnki.1006-1630.2017.06.006