基于等几何分析的非均质股骨近端模型的受力分析

产启平，陈 龙

(上海理工大学 机械工程学院，上海 200093)

基于等几何分析的非均质股骨近端模型的受力分析

产启平，陈 龙

(上海理工大学 机械工程学院，上海 200093)

人工股骨置换手术是目前治疗股骨骨折比较成熟的一种方法。但由于人体骨骼的复杂性，采用单一材料均匀分布进行力学性能分析时难以得到准确结果。文中采用3种不同的材料赋值方法进行材料非均质建模以提高模型建模精度，采用等几何分析方法以提高性能分析精度。从股骨几何点云和材料灰度信息数据出发，用体参数化的建模理论，得到人体股骨的B样条体参数化模型，然后采用中心点插值、节点插值、高斯积分点3种插值法赋予模型10种不同的材料，得到非均质模型。根据有限元基础理论推导出刚度矩阵，并施加边界和约束条件，最终通过求解线性方程组得到静力学分析结果。实验表明，文中建模方法精确高效，得到的结果合理且更接近实际。

等几何分析; 非均质; 体参数化; 股骨; 静力学分析

目前治疗股骨骨折的常见方法是人工股骨置换手术，鉴于股骨的重要性，所以对置换假体的性能要求也非常高。置换假体不仅要接近真实形态，而且要承受的住日常生活所施加的载荷，使其避免出现断裂、错位等现象。因此置换前，需对股骨进行精确的模型构建和力学性能分析。

对于股骨的分析需要建立精确的三维模型和准确的材料赋值，这也是进行股骨力学分析的基础和关键。由于股骨结构的复杂性，几何形态的不规则性，研究表明直接用CAD、CAE软件进行建模很困难[1]。目前国内外对于人体股骨的重建有多种方法：(1)三维坐标仪建模法[2]；(2)通过扫描图片利用CAD逆向三维重建出模型[3]；(3)组织切片法[4]。另一方面，目前很多关于股骨的研究是将其材料假设为均匀分布的密质骨和松质骨，更有将其设置为一种材料的研究，针对股骨的复杂性，这样的赋值会对研究产生严重的误差。本文结合真实股骨的材料分布，采用3种插值方法对股骨模型进行10种不同材料的赋值，实现了股骨材料建模。分析方面目前大多数采用的是有限元方法[5-7]。由于传统有限元分析中CAD设计模型和CAE分析模型往往是在不同的平台下完成，导致CAE模型的分析结果不能够准确反应原CAD模型的特征，而且对于越复杂的产品模型，误差越大。

HUGHES[8-11]等在传统有限元方法基础上提出了等几何分析方法(Isogeometric Analysis，IGA)。等几何分析方法基于有限元分析方法的等参单元思想，将模型设计中用于表达几何模型的非均匀有理B样条(NURBS)的基函数作为形函数，实现了计算机辅助设计(CAD)和计算机辅助工程(CAE)的无缝结合。

本文采用等几何分析方法对股骨进行分析。由于几何模型可直接用于分析，不需要经过转换、处理等操作，显著提高了求解精度和计算效率。

1 股骨体参数化模型构建

体参数化模型的构建，是通过对已知边界面进行体插值，实现与模板模型的一一映射，体参数化模型是等几何分析的基础。体参数化模型的构建过程如图1所示。

图1 体参数化模型构建

(1)点云数据预处理。点云分片要求将点云模型分解为数目有限、具有相似特征且互不重叠的子区域。在参照特征边界点的前提下，采用交互式分割法，将点云模型分割为6个点云面片。

每个完成分割的点云面片有4条边界，采用散乱点云最小二乘B样条曲面拟合算法来实现6个点云面片的曲面拟合。其步骤为：1)根据分片曲面的散乱点及其边界曲线构造基面；2)将散乱数据点投影到已构造好的参数曲面上进行投影参数化；3)采用最小二乘法 实现散乱点云的曲面初始重建；4)将初始重建曲面作为基面迭代。再将曲面拼接起来形成一个封闭的空间。

(2)B样条体构建。在对六曲面拟合完成以后，只是得到体参数化模型的表面控制点，通过对六个表面的曲面片进行插值得到初始内部控制点，为提高网格顶点的质量，需要对这些控制点进行微调，避免网格点的自交，从而得到最终的体内控制点。在所有控制点确定之后，即可得到B样条体的可视化模型。根据B样条理论，三维NURBS体的表达式如下

(1)

其中，S(ξ,η,ζ)指用空间中的点(ξ,η，ζ)表示的三维参数体；Pi,j,k(i=0,1,…,n;j=0,1,…,m;k=0,1,…,l)表示控制点；Ri,j,k(ξ,η,ζ)表示3变量有理基函数，其表达式为

(2)

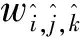
基于上述理论，然后按照前述方法构建了股骨近端参数化模型如图2所示，可以看出，基于体参数化方法构建的人体股骨三维模型和真实的人体股骨模型结构外观相吻合。

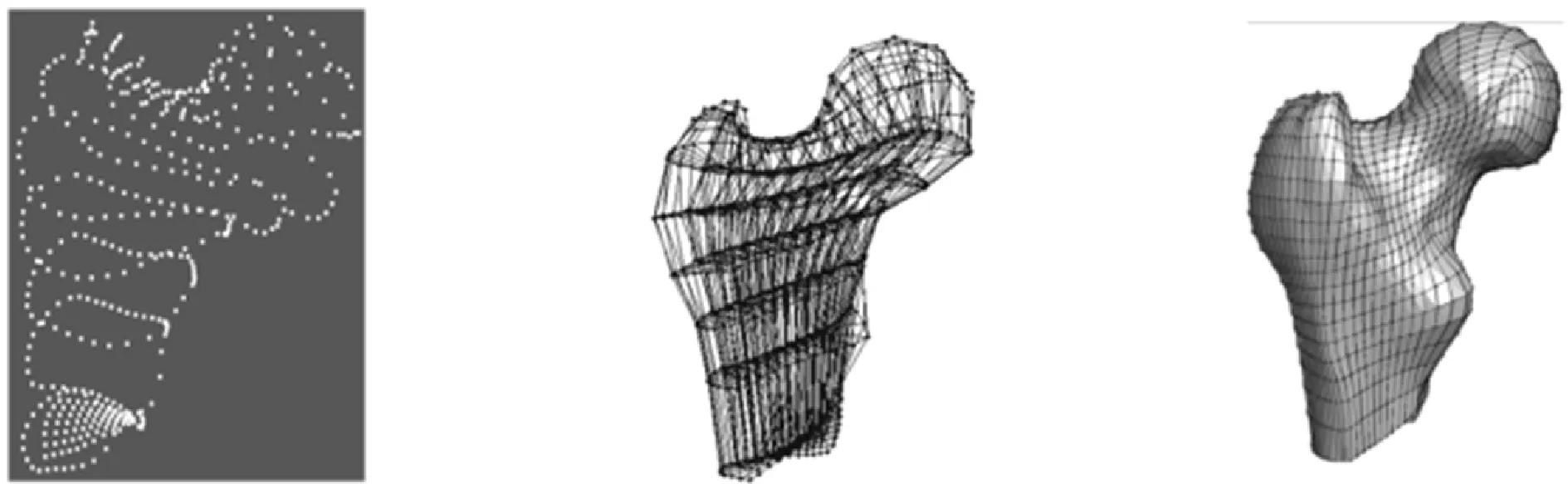
图2 股骨近端体参数化模型

2 股骨体参数化模型材料赋值

目前国内外关于骨骼的分析材料的选取，只考虑密质骨和松质骨两种材料的简化，甚至只考虑单均一材料的影响。传统这种材料赋值方法远远不能够满足分析的要求。根据张国栋[12-13]等人关于骨骼材料赋值的研究和综合考虑计算效率，将股骨按照图像的灰度值完成10种材料特性的赋值(见表1)，其中泊松比[14]为0.3，弹性模量为Mimics提供经验公式

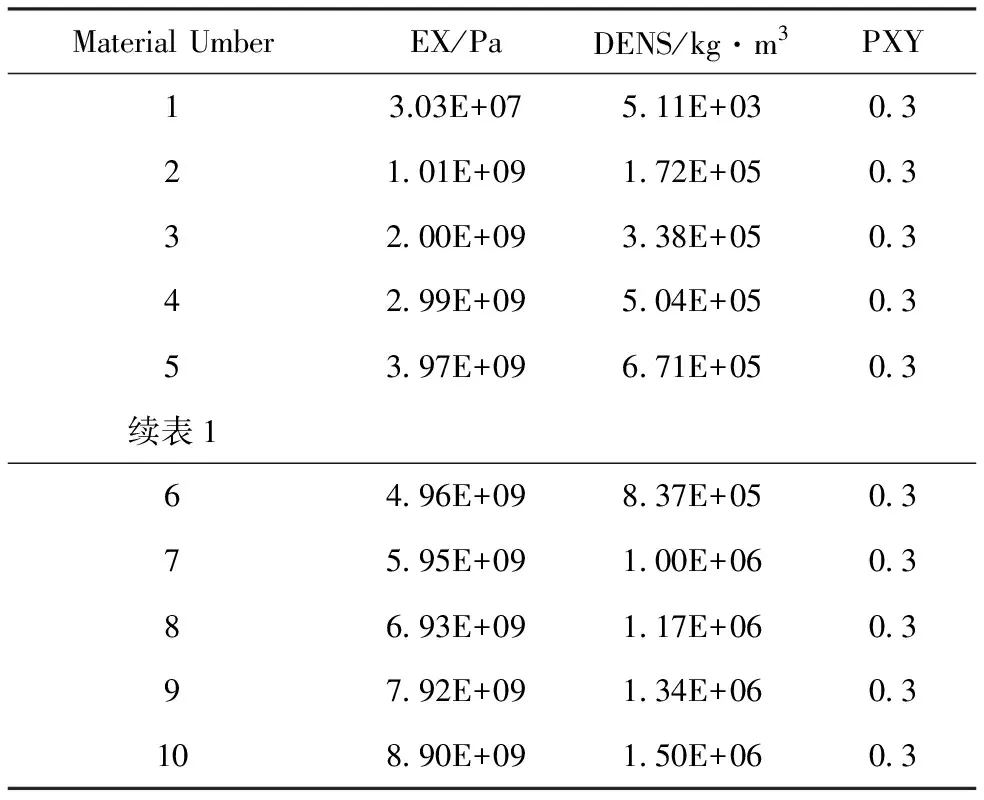
Density=-13.4+1 017×Grayvalue (3)

对于非均质材料，希望B样条的密度函数 能够应用于各种分析中，对于分析所用的密度可以用不同的方法估算得到。在本文提供了3种方法来估算有限单元中，B样条表达的密度分布。

(5)

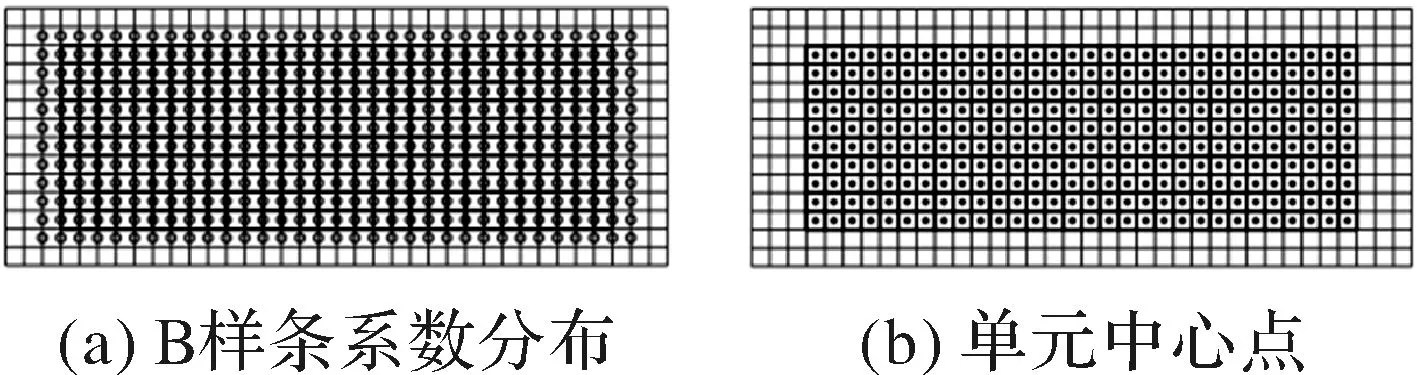
图3 B样条系数与单元中心

(2)基于节点的近似值。密度由单元节点估算而来。即单元密度为

(6)

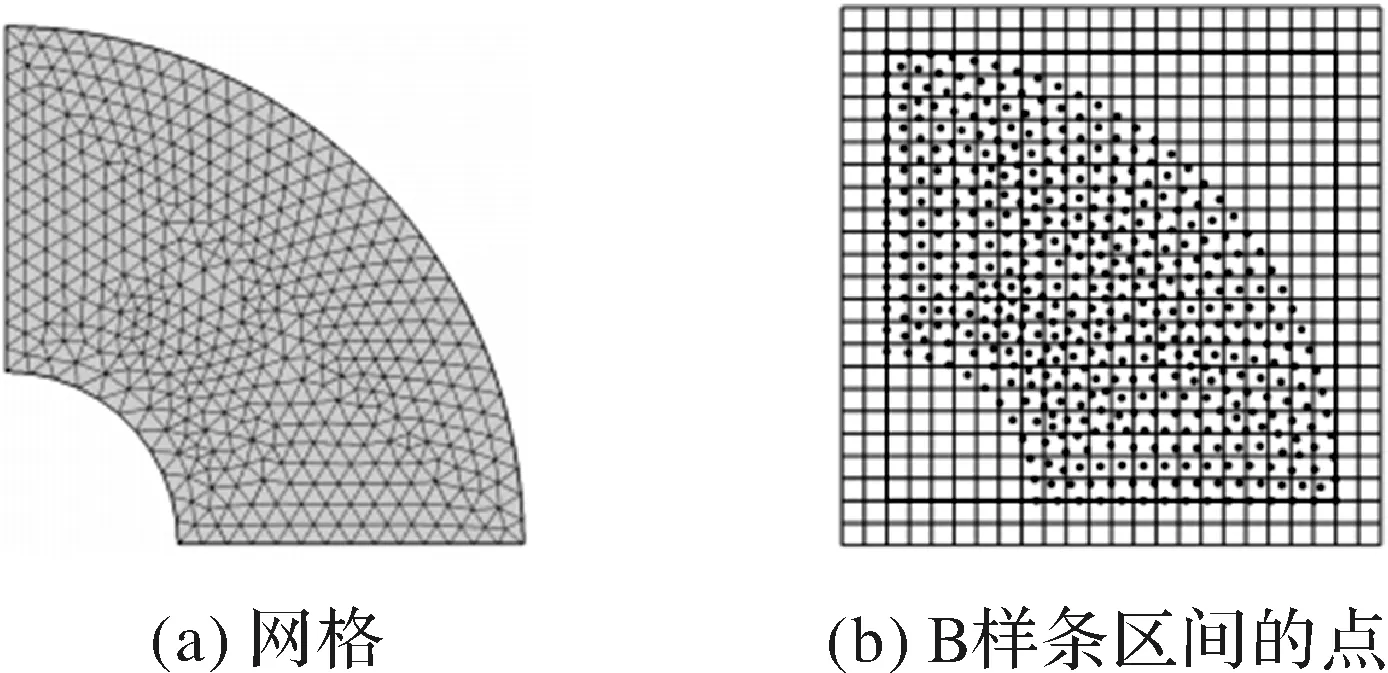
图4 网格与节点

(3)基于高斯积分点的近似值。密度由单元积分点处的值估算得到。则单元密度为

(7)

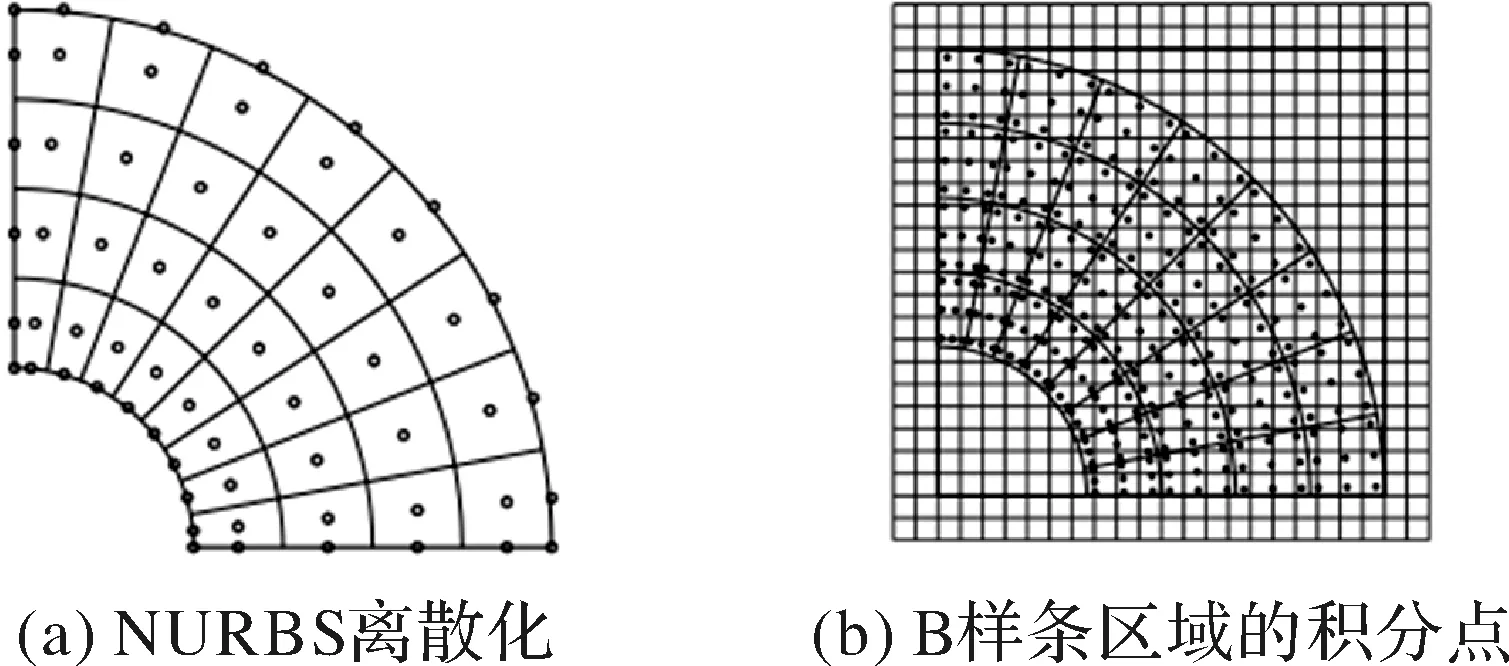
图5 NURBS离散化与积分点

3 等几何分析方法

等几何分析和传统有限元最本质的区别是在于基函数的选择，其他方面很相似， 根据有限元方法中的虚功原理及最小势能原理推导出单元的刚度矩阵

(8)

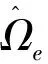
(9)

其中，D0是涉及单元材料的弹性矩阵；ωj是积分点j处的权重；E(ρ(pj))是积分点j处的弹性模量。用SIMP插值算法，弹性模量可以表示为

E(ρ(x))=Emin+ρ(x)s(E0-Emin)

(10)

其中，E0是固体的刚度；s是惩罚系数；ρ(x)是单元的物理密度；Emin是最小弹性模量，避免出现刚度矩阵奇异。

如果ρ是常数，所有积分点的密度被认为和单元中心处的密度一样，即ρ(pj)=ρ(pc)。因此单元的刚度矩阵可以被简化为

(11)

(12)

其中，Nk,j表示节点k在单元的第j个积分点处估算的形函数。

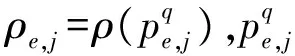
(13)

得到单元刚度矩阵后，借鉴传统有限元中整体刚度矩阵组装的方法进行组装得到整体刚度矩阵K，从而得到总体平衡方程

Kd=F

(14)

其中载荷矢量

(15)

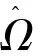
4 股骨模型的分析

基于上述原理与流程，分析人体正常站立位时股骨近端的纵向受压情况。本文简化边界条件，将股骨上端施加600 N竖直向下的压力，股骨下端定为完全约束，即底面上所有的节点的自由度为0，分别采用3种材料赋值方法对模型赋值进行分析计算，计算结果如图所示。

图7 应力云图

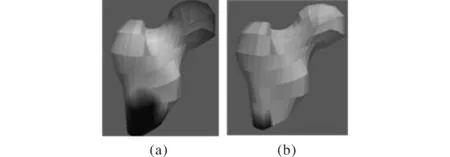
图8 单一材料分析结果

图6分别为3种赋值方法得到的各点的位移变化情况，图7分别为3种方法得到的应力分布特征。从上述分析结果可以看出，3种赋值方法得到的分析结果基本相同，应力主要集中在股骨的上下两端，其3种赋值方法所得最大应力分别为13.6 MPa，14.1 Mpa和12.9 MPa，与文献[17]中股骨纵向受压仿真得到的结果非常接近。图8为采用单一材料分析得到的结果，显然应力集中的地方不是很明显，且最大应力为9.8 MPa，与本文仿真结果相差较大。因此本文能更好的显示出股骨在载荷作用下的应力分布特征。

5 结束语

本文采用体参数化建模方法，对股骨模型进行了精确、快速重建，并通过扫描得到的灰度值，采用3种不同的方法对股骨进行材料赋值，得到非均质股骨模型，使得所建模型更加逼真，从而提高了分析的可靠性。对股骨纵向受力分析采用等几何分析方法来代替传统的有限元方法，从而使得设计模型与分析模型一致，避免了因模型转换带来的误差，进一步提高了计算精度。

[1] 胡小春,郭松青,叶铭.基于CT图像建立人体足部骨骼三维有限元模型的研究[J].合肥工业大学学报,2006,28(9): 1189-1191.

[2] 张美超,廖进民,李敏,等.激光三维扫描系统重建下颌骨[J].第一军医大学学报,2004,24(7):756-757.

[3] 胡鑫,习俊通,顾冬云,等.髋关节CAD模型的建立与几何形态分析[J].北京生物医学工程,2003,22(2):116-120.

[4] 李安安,刘谦,龚辉,等.“虚拟中国人男性一号”高精度骨骼系统的三维建模[J].中国临床解剖学杂志,2006,24(3): 292-294.

[5] 姜海波,葛世荣.基于CT扫描人体股骨的有限元分析[J].工程力学,2007,24(10)：156-159.

[6] 罗承刚,龚宪生.近端股骨的非均匀及各向异性有限元模拟[J].重庆大学学报，2004 (2):20-23.

[7] 刘海,谢力勤,徐孝根,等.给定荷载下的骨骼重建的有限元分析[J].清华大学学报,2002,42(8):1079-1082.

[8] T J R Hughes,J A Cottrell,Y Bazilevs. Isogeometric analysis:CAD,finite elements,NURBS,exact geometry and mesh refinement[J].Computer Methods in Applied Mechanics Engineering,2005(194):4135-4195.

[9] Cottrell J A,Hughes T J R,Bazilevs Y.Isogeometric analysis: toward integration of CAD and FEA[M].New York:Wiley Press,2009.

[10] Kim H J,Seo Y D,Youn S K. Isogeometric analysis for trimmed CAD surfaces[J].Computer Methods in Applied Mechanics and Engineering, 2009(198):2982-2995.

[11] Noor A K.Evaluation of element stiffness matrices on CDC STAR-100 computer[J].Computers and Structures,1978(9):151-161.

[12] 张国栋,廖维靖,陶圣祥,等.股骨颈有限元分析的赋材料属性方法探讨及有效性验证[J].中国组织工程研究与临床康复,2009,13(52) :8436-8441.

[13] Lengsfeld M,Schmitt J,Alter P,et al. Comparison of geometry-based and CT voxel-based finite element modelling and experiment validation[J].Medicine Engineering Physics,1998,20(7):515-522.

[14] 高建伟,陈龙.基于等几何分析的股骨模型静力学分析[J].计算机仿真,2015, 32(5): 340-343.

[15] 陈树广.基于病例CT图像的健康股骨头建模研究[J].计算机仿真,2009,26(9): 172-175.

[16] 韩树洋,葛世荣.人工全髋关节置换术对天然股骨生物力学行为的影响[J].医用生物力学,2010,12(6):471-474.

[17] 陈研妤,应祖光,朱振康,等.股骨纵向受压时的应力分布特征分析[J].固体力学学报,2016,37(5):74-78.

Stress Analysis of Heterogeneous Femoral Proximal Model by Using Isogeometric Analysis

CHAN Qiping,CHEN Long

(School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

Artificial femoral replacement surgery is a method for the treatment of femoral fractures. However it is difficult to get a currate results by using. Because of the human skeleton is very complex, uniform distribution or single material simulation. In this paper, three different interpolation methods were used to assign the 10 different materials to the model, and the femur was modeled and analyzed by geometric analysis. The geometrical information expressed in the form of point cloud and the material data expressed in grayscale information were used as the basis of geometric modeling and material modeling. The parametric geometry of the femur was obtained by the parametric construction theory of body model. Then, we used the central point interpolation, the node interpolation and the Gaussian integral point interpolation method to assign the model 10 different materials to obtain the heterogeneous model. According to the principle of virtual work and the minimum potential energy principle, the element stiffness matrix and the overall stiffness matrix were deduced, and the boundary condition was imposed. Finally, the statics analysis results were obtained by solving the linear equations. Experiments showed that the modeling method was accurate and efficient, and the heterogeneous femur model obtained by the three interpolation methods was reasonable and closer to the actual result.

isogeometric analysis; heterogeneity; volume parameterization; femur; static stress analysis

2017- 03- 29

国家自然科学基金(51475309)

产启平(1991-)，男，硕士研究生。研究方向：CAD/CAE。陈龙(1978-)，男，博士，副教授。研究方向：产品计算设计、产品快速设计、图像处理技术等。

TN04；TP391.9

A

1007-7820(2018)02-015-05