随机自适应差分进化算法
2018-01-06邹德旋
沈 鑫,邹德旋,张 鑫
(江苏师范大学 电气工程及自动化学院,江苏 徐州 221116)
随机自适应差分进化算法
沈 鑫,邹德旋,张 鑫
(江苏师范大学 电气工程及自动化学院,江苏 徐州 221116)
针对差分进化算法存在早熟收敛且与理想最优值相差甚远等缺陷。随机自适应差分进化算法被提出,该算法采用随机选择策略的变异操作,再加小概率扰动;对变异因子和交叉概率进行自适应操作,以满足算法不同阶段的要求,其中交叉概率利用种群个体平均适应度值作对比,有利于充分利用种群信息。对几个标准函数进行测试并将该算法与其他4种方法进行比较,结果显示该算法的优化性能比其他方法好,具有较好的跳出局部最优的能力和收敛精度。
差分进化算法;随机变异;扰动;自适应操作
差分进化(Differential Evolution,DE)算法[1]是在种群内寻找最优值的智能优化算法。目前,DE算法在神经网络优化[2]、电力系统无功优化[3]、约束优化[4]、车间调度[5]、控制[6]等方面得到了广泛应用。DE算法到了进化后期,种群的多样性降低,容易出现早熟收敛和收敛精度不高的问题。
为克服以上缺点, 针对DE算法的改进主要在以下几方面:控制参数[7]、变异策略[8-9]、种群结构[10]、混合优化算法[11-13]。文献[14]提出了随机变异差分进化算法(Random Mutation Differential Evolution Algorithm, RMDE)。本文在此基础上提出了一种随机自适应差分进化算法(Self-adaptive Differential Evolution Algorithm with Random Mutation,SRDE),SRDE算法在RMDE算法的基础上又增加了对参数的自适应操作,使其收敛精度更高,跳出局部最优解的能力更强。
1 标准的差分进化算法
差分进化算法的基本思想是对初始化种群中的个体,进行变异、交叉、选择操作,按照"适者生存"的原则来保留优秀个体,实现种群更新。标准差分进化算法的步骤主要有以下5步:
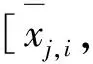
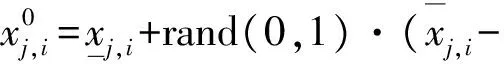
(1)
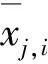
(2)变异 DE通过差分向量实现个体变异,在变异中最常用的策略是DE/rand/1/bin,即
(2)

(3)

(4)选择 DE基于贪婪原则选择进入下一代的个体。
(4)
(5)终止判断。若满足条件(达到最大迭代数要求),则停止搜索,输出最优解;否则,返回步骤(2),继续执行变异,交叉和选择操作。
2 随机自适应差分进化算法
SRDE算法在RMDE算法的基础上,增加了参数自适应操作。
2.1 随机变异操作
变异操作是DE算法中非常重要的步骤。DE算法采用固定变异策略DE/rand/1,可以在算法搜索初期进行全局搜索,保证种群多样性,但无法满足搜索后期局部搜索要求,而采用DE/best/1策略可以加快搜索速度,但容易出现早熟收敛。为了既保证种群多样性,又加快搜索速度。本文借鉴了RMDE算法中的随机变异方法,在DE/rand/1和DE/best/1策略中随机选择,以适应不同阶段的要求。表达式为
(5)
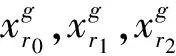
2.2 扰动操作
在种群向最优解进化过程中,算法可能搜索到的当前最优解是全局最优解,也可能是局部最优解。如果是局部最优解时,这时有可能陷入其中,跳出局部最优就显得非常重要;如果是全局最优解,则个体不会被淘汰。针对这种情况,SRDE算法使用了一种小概率扰动策略,使其跳出局部最优解,避免早熟收敛。表达式为
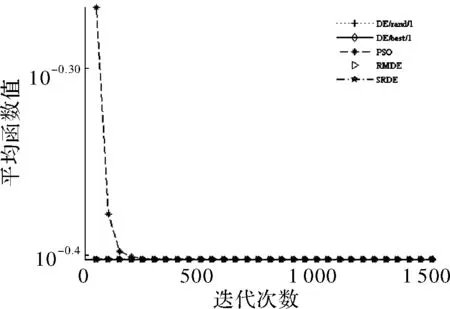
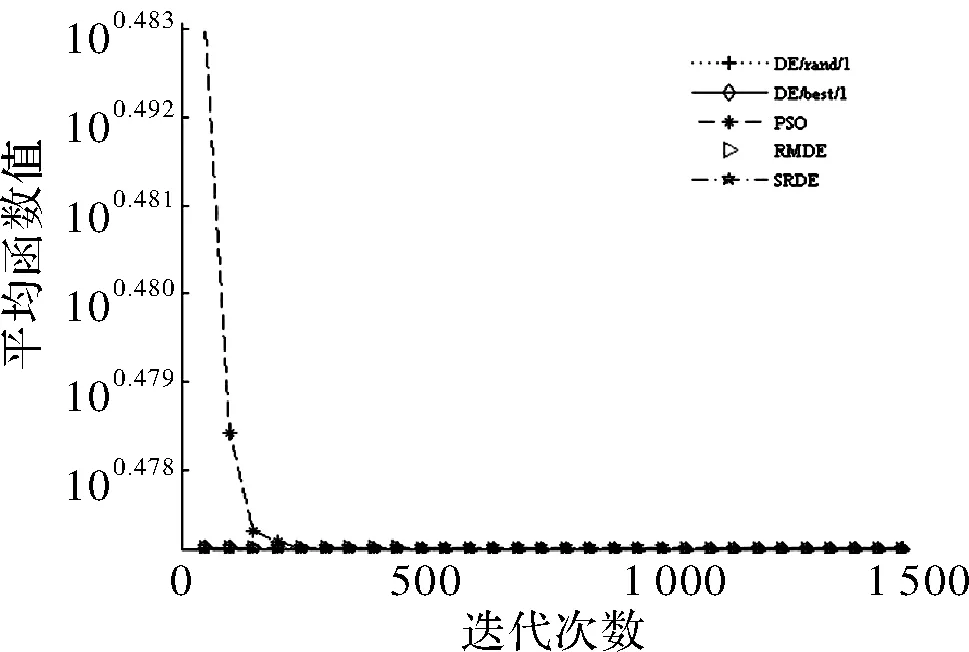
if rand (6) else end 其中,xmin和xmax分别为搜索的上下边界,p一般取>0.9,p=0.99。 F和CR采取自适应操作是为了满足算法各个阶段的要求,以平衡全局搜索和局部搜索。 2.3.1 自适应变异因子 变异因子是用来对差异矢量进行缩放,根据要求SRDE算法将变异因子动态自适应变化。具体表达为 (7) 2.3.2 自适应交叉概率 自适应交叉概率是根据上一代个体的适应度值与上一代种群的平均适应度值比较来自适应调整。分两种情况讨论:一种是上一代个体的适应度值小于等于上一代种群的平均适应度值采用式(8i);另一种是上一代个体的适应度值大于上一代个体的平均适应度值采用式(8ii)。当种群进化第一代时采用式(9)。具体表达式为 (8) (9) 步骤1初始化种群,设置参数,主要包括种群最大进化代数、种群规模、变异因子的最大最小值、交叉概率的最大最小值、种群的边界; 步骤2计算种群个体的适应度值,并求出最优解对应的最优个体和平均适应度值; 步骤3实施随机变异自适应操作,并加小概率扰动; 步骤4实施自适应交叉操作; 步骤5利用贪婪原则进行选择,较好的个体将存活,进入下一代; 步骤6终止判断,当种群进化到最大代数时,输出最优解,算法结束;否则,g=g+1,返回步骤2。 本文选取7个标准测试函数[15]进行测试。为了验证SRDE算法在函数优化的性能,将SRDE算法与DE/rand/1/bin策略的DE算法、DE/best/1/bin策略的DE算法、RMDE算法、PSO算法进行比较。7个标准测试函数的具体表达式为 仿真实验使用Matlab8.3软件来编程实现,且电脑配置为Intel(R) Core(TM) i5-2450M CPU @ 2.50 GHz。算法的参数设置如下:DE/rand/1/bin和DE/best/1/bin策略的DE算法中F=0.5,CR=0.9;RMDE算法的参数值见文献[14];PSO算法的学习因子c1=c2=2,惯性权重w由0.9到0.4线性递减,粒子最大速度100;SRDE算法的变异因子和交叉概率最小值,最大值分别是Fmin=0.1,Fmax=0.8,CRmin=0.1,CRmax=0.9,其他参数值与RMDE算法中的相同;种群规模NP=100;算法对不同测试函数的最大迭代次数在表中给出;种群的边界范围是[-100,100];维数D=100。 表1是函数优化的数据,算法对f1~f5的优化是维数为100时,算法对f6和f7的优化是维数为2时,各个算法性能比较将通过搜索的最优值、平均值、标准差得出。每一种算法都独立进行30次实验。 表1 函数优化结果 表1是算法在高维和2维时的数据,从表中可以看出DE/best/1/bin策略的DE算法和PSO算法的最优解、平均值、标准差都较大,说明DE/best/1/bin策略的DE算法和PSO算法虽然可以加快搜索速度,但容易陷入局部最优。对f1、f2、f3、f4、f5函数而言,SRDE算法搜索到的最优解和收敛精度比RMDE算法好;对f3、f6、f7函数而言,SRDE算法都可以找到理想最优解。表中的平均值代表算法的平均优化性能,这也是重要的评价指标,下面的收敛曲线也是用平均函数值得到的平均优化曲线。 综上所述,SRDE算法跳出局部最优的能力和收敛精度好于其他4种方法,说明对参数的自适应是必不可少的,特别是将种群平均值引入来对比,充分利用其他个体的信息。从求解高维函数来看,SRDE算法对于求解高维问题有一定的优势。 图1~图5分别是100维时函数f1~f5的收敛曲线,图6、图7分别是2维时函数f6和f7的收敛曲线,横坐标表示迭代次数,纵坐标表示平均函数值。 图1 收敛曲线 图2 收敛曲线 图3 收敛曲线 图4 收敛曲线 图5 收敛曲线 图6 收敛曲线 图7 收敛曲线 从仿真曲线可以看出,SRDE算法明显要好。对函数f1、f3、f4、f5而言,前期SRDE算法下降的比RMDE算法慢,但到了后期搜索速度加快,收敛精度变高。在表1中,函数f3在SRDE算法的搜索下可以找到理论最优解,但所需要的最大迭代次数很大,从而需要更长的时间,从这个函数可以看出SRDE算法对某些函数而言需要的迭代次数很大,才能搜索到全局最优解。综上,SRDE算法在高维时的优化性能比较优越。 SRDE算法将RMDE算法中的随机策略选择,小概率扰动和参数自适应结合起来用于函数优化,更好的利用了种群信息和有效避免了早熟收敛。将SRDE算法、DE/rand/1/bin策略的DE算法、DE/best/1/bin策略的DE算法、RMDE算法、PSO算法用来优化7个经典函数并对结果进行对比,结果表明:SRDE算法具有较强的全局搜索能力和收敛精度。在接下来的工作中,将改进SRDE算法使之收敛速度加快。 [1] Storn R,Price K.Differential evolution-a simple and efficient adaptive scheme for global optimization over continuous spaces[J].Journal of Global Optimization,1997,11(4):341-359. [2] 李目,何怡刚,周少武,等.一种差分进化算法优化小波神经网络及其在弱信号检测中的应用[J].计算机应用与软件,2010,27(3):29-31. [3] 马立新,孙进,彭华坤.多目标差分进化算法的电力系统无功优化[J].控制工程,2013,20(5):953-956. [4] 閤大海,李元香,龚文引,等.一种求解约束优化问题的自适应差分进化算法[J].电子学报,2016,44(10):2535-2542. [5] 王万良,范丽霞,徐新黎,等.多目标差分进化算法求解柔性作业车间批量调度问题[J].计算机集成制造系统,2013,19(10):2481-2492. [6] 李爱军,王景,李佳,等.基于差分进化算法的飞行控制律评估[J].模式识别与人工智能,2014,27(3):256-262. [7] 张雪霞,陈维荣,戴朝华.带局部搜索的动态多群体自适应差分进化算法及函数优化[J].电子学报,2010,38(8):1825-1830. [8] Qin A K,Huang V L,Suganthan P N.Differential evolution algorithm with strategy adaptation for global numerical optimization[J].IEEE Transactions on Evolutionary Computation,2009,13(2):398-417. [9] 谭跃,谭冠政,伍雪冬.基于交叉变异策略的双种群差分进化算法[J].计算机与应用,2010,46(18):9-12. [10] 夏慧明,王志刚,周永权.多种群自适应差分进化算法[J].小型微型计算机系统,2014,35(4):850-853. [11] 王志,胡小兵,何雪海.一种新的差分与粒子群算法的混合算法[J].计算机工程与应用,2012,48(6):46-48. [12] 杨俊,魏静宣.梯度策略自适应差分进化算法[J].电子科技,2016,29(1):25-27. [13] 范瑜,金荣洪,耿军平,等.基于差分进化算法和遗传算法的混合优化算法及其在阵列天线方向图综合中的应用[J].电子学报,2004,32(12):1997-2000. [14] 欧阳海滨,高立群,孔祥勇.随机变异差分进化算法[J].东北大学学报:自然科学版,2013,34(3):330-334. [15] Zou Dexuan,Gao Liqun,Wu Jianhua,et al. Novel global harmony search algorithm for unconstrained problems[J]. Neurocomputing,2010,73(16-18):3308-3318. Self-adaptive Differential Evolution Algorithm with Random Mutation SHEN Xin,ZOU Dexuan,ZHANG Xin (School of Electrical Engineering and Automation,Jiangsu Normal University,Xuzhou 221116,China) Aiming at the defects of differential evolution, such as the premature convergence and optimal value of differential evolution is far from the ideal optimal value. Self-adaptive differential evolution algorithm with random mutation was presented. Random choice strategy was adopted to execute mutation operation by the algorithm, which added to small-probability disturbance. To meet the requirements of different stages of the algorithm,the mutation factor and crossover rate performed the adaptive operation. The crossover rate was compared with the average of the fitness of individuals, which was beneficial to make full use of population information. Several standard functions were tested and the SRDE algorithm was compared with the other four methods. The results show that the optimization performance of SRDE algorithm is better than other methods, and it is better to jump out of local optimal ability and convergence precision. differential evolution algorithm;random mutation; disturbance;self-adaptive operation 2017- 03- 21 国家自然科学基金青年基金(61403174) 沈鑫(1994-),男,硕士研究生。研究方向:群智能算法。邹德旋(1982-),男,博士, 副教授。研究方向:群智能算法。张鑫(1994-),男,硕士研究生。研究方向:群智能算法。 TN911;TP306.1 A 1007-7820(2018)02-051-052.3 自适应变异因子和自适应交叉概率

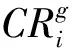
2.4 随机自适应差分进化算法具体步骤
3 实验仿真与分析


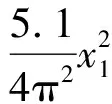
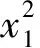

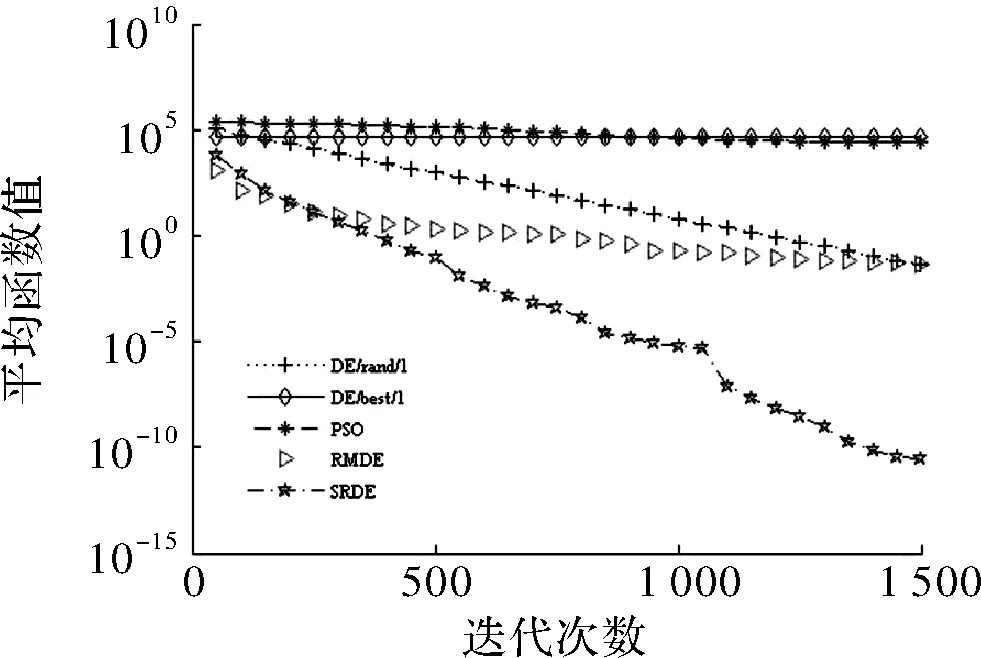
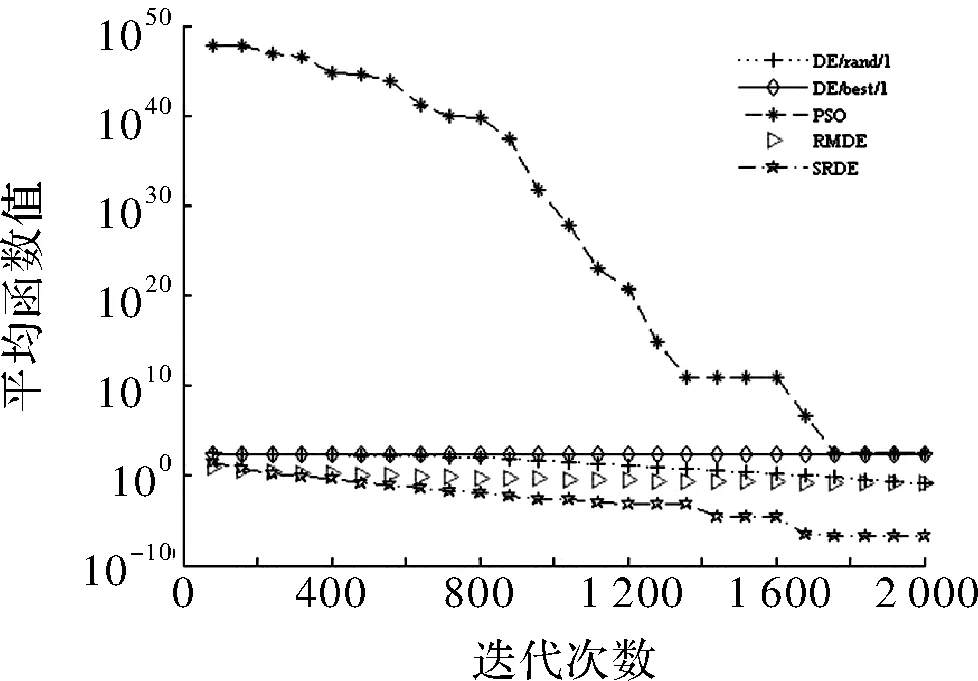
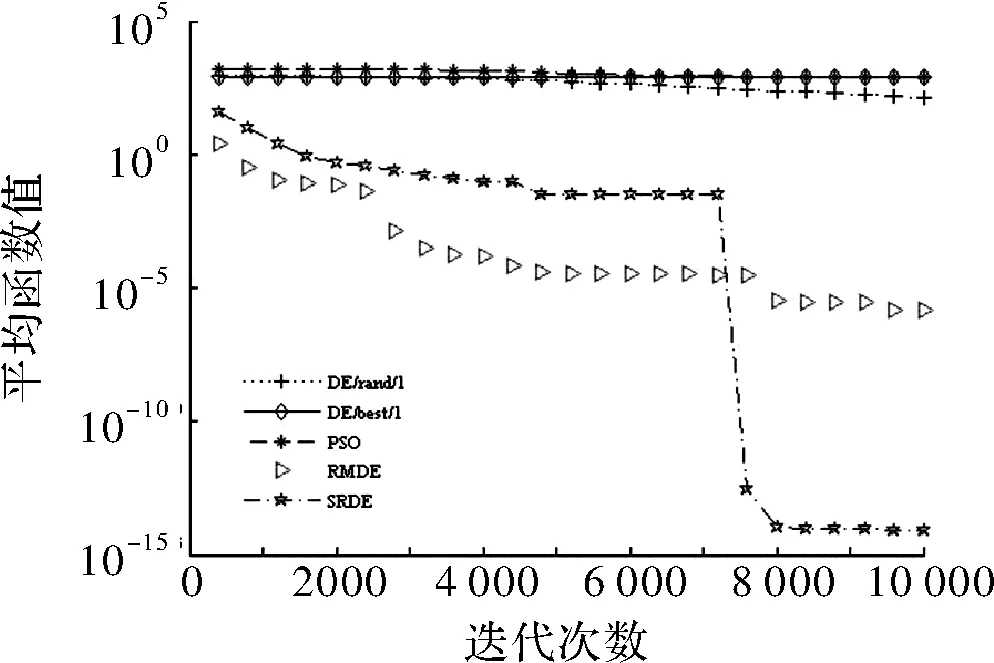
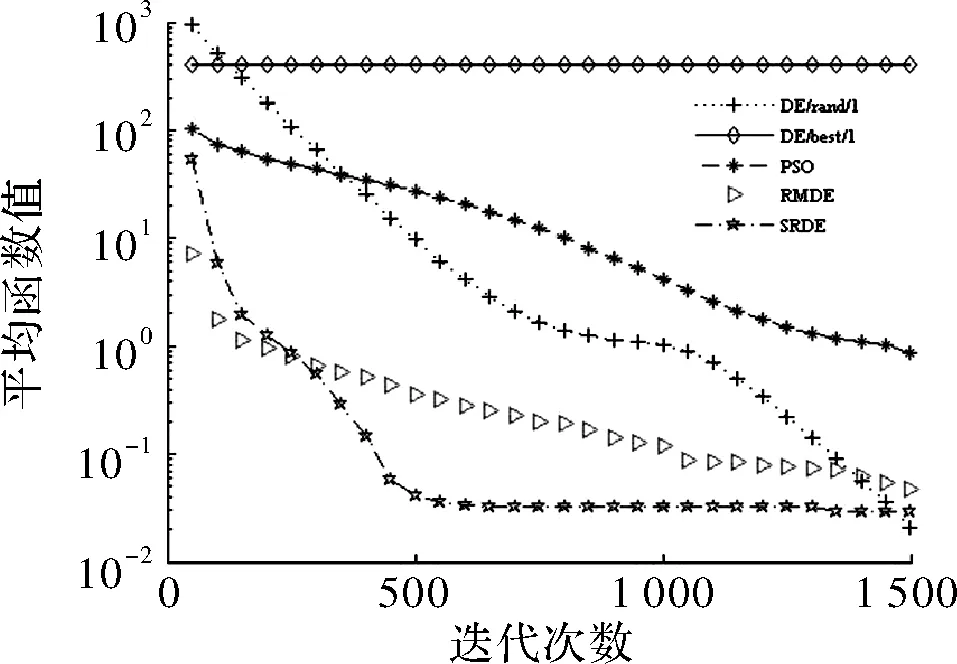
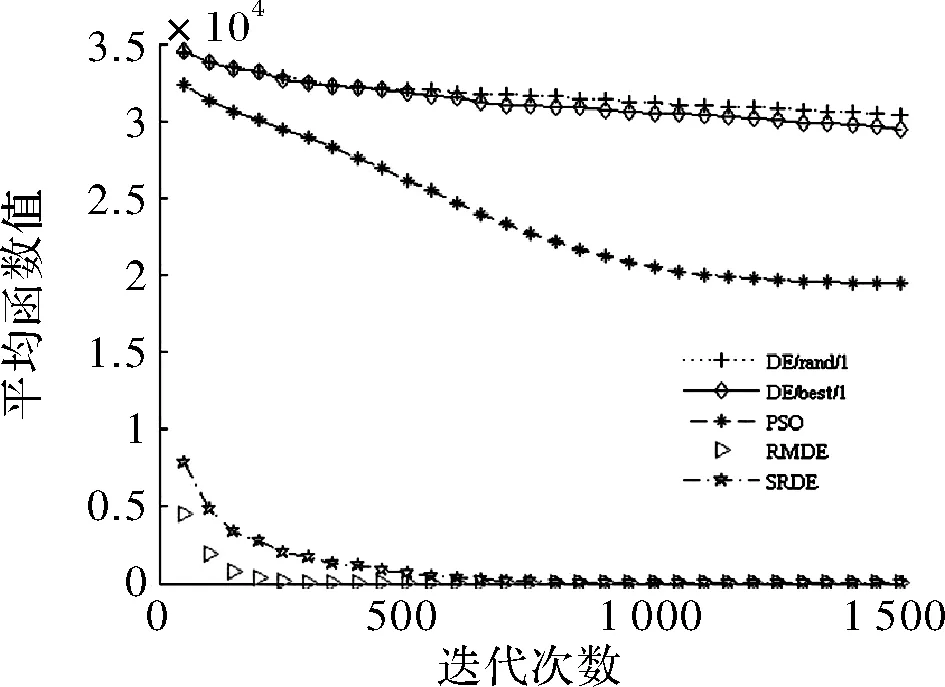
4 结束语
