基于HAR-RV-CJ模型的天然气价格预测

吴东武，朱帮助

（1.五邑大学 经济管理学院，广东 江门 529020；2.暨南大学 管理学院，广州 510632）

0 引言

国内外相关文献，从制度、统计、模型等视角探讨了天然气消费、定价机制、天然气价格波动特征等，为管理层、投资者及消费者从宏观层面、影响因素把握天然气消费以及价格变化趋势提供理论支持。但由于未涉及天然气市场自身的异质性，因此，未能从实操决策层面提供更多支持。（1）忽略多尺度、多时段交易方式对天然气价格波动影响研究。市场交易者存在交易偏好，导致不同交易时段，如天、周、月出现集中交易或分散交易现象，引发天然气价格波动。（2）缺少对天然气价格已实现波动率及其特征进行研究。对天然气价格RV建模和预测，有助于天然气定价、天然气资源配置、天然气价格风险测度，揭示天然气价格变化特征。（3）未对天然气价格RV影响因素进行研究。因此，本文首先根据二次幂变差理论，把天然气价格 p（t）分解为连续样本路径方差和跳跃变差；其次，依据连续样本路径方差和跳跃变差定义天然气价格已实现波动率；第三，根据天然气市场异质性，构建天然气价格HAR-RV-CJ模型；第四，应用Henry Hub天然气数据对模型进行实证研究，考察天然气价格RV的统计特征，测试市场噪音对离散跳跃方差的影响，检测HAR-RV-CJ模型对RV预测效果。

1 研究方法

1.1 二次幂变差与已实现波动率

假设t时刻天然气对数价格是 p（t），服从连续跳跃扩散过程，则其随机差分方程写成：

其中，u（t）连续且局部有界，表示漂移系数。 σ（t）（＞0）是随机波动，表示扩散系数。w（t）是标准布朗运动。ϕ（t）dq（t）是对数价格中跳跃部分，其中 ϕ（t）=p（t）-p（t-1），表示t时刻对数价格过程离散跳跃成份的幅度。若t时刻有跳跃发生，则 dq（t）=1 ，否则 dq（t）=0 。累积收益率r（t）=p（t）-p（0），p（t）在区间 [0，t]（0≤s≤t）上的二次幂变差（Bi-power Variation）定义为：

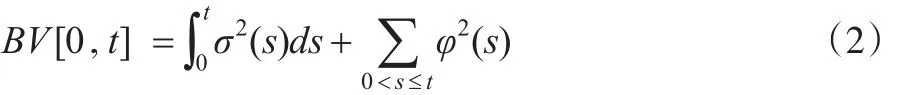
根据Barndorff-Nielsen（2002）[2]的研究成果，若天然气价格不存在跳跃，当Δ→0时，RV收敛于积分波动率，式（3）可写成：

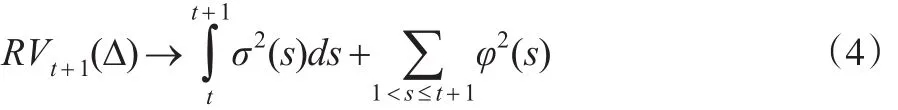
若天然气价格存在跳跃，RV依概率收敛到二次幂变差过程。Barndorff-Nielsen and Shephard（2004）[3]给出已实现二次幂变差（Realized Bi-power Variance）：

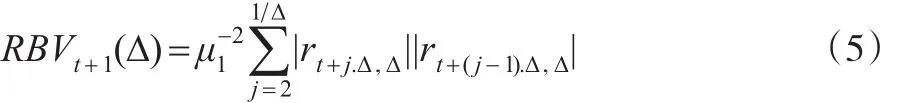
其中 μ1==E（Z），表示服从标准正态分布随机变量Z的绝对值的数学期望。当Δ→0时，RBV收敛于积分波动率：

因此，根据式（4）和式（6），可计算出二次幂变差中的离散跳跃成份，即是当Δ→0时，有：

由式（7）看出，在加入跳跃过程后，RV的收敛结果除包含积分方差外，还包含了跳跃对波动的影响，而RBV仍收敛到积分方差。对于任意给定的数据，由式（7）计算得到的JV不一定是正数，因此，为确保JV的日间估计量非负，重新定义式（7）：

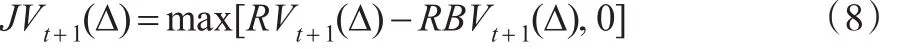
1.2 Jt+1，α 、Ct+1，α 估计

用式（8）可计算RV中的JV成份来检测日内回报率中的跳跃成份。为了提高JV测量的精度，本文用Zt+1（Δ）统计量（Andersen，2011）[4]来甄别RV中显著的 JV 成份。

其中的TQt+1（Δ）是一个三次方幂，根据下式进行估计：

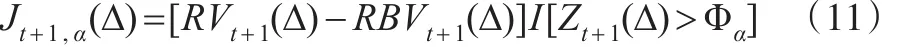
其中,α代表显著性信水平,I[⋅]是示性函数,用来识别Zt+1（Δ）统计量在超过高斯分布Φα关键值时的重要性。而连续样本路径方差Ct+1，α（Δ）可以用下式进行估计：

经过变换后，对于 Φα＞0，式（11）、式（12）能保证Jt+1，α（Δ）≥ 0 、Ct+1，α（Δ）≥ 0 。

1.3 市场噪音对 Jt+1，α、Ct+1，α的影响

天然气交易过程中，若受到市场微观结构噪音影响，连续观察到的对数价格过程不服从半鞅过程这一假设，导致RBV的计算出现偏差。为了消除这些偏差，Zhang等（2005）[5]提出双尺度估计法计算RV和RBV。作为进一步的稳健性检验，Andersen等（2012）[6]用平均实现波动率法估计RV和RBV，估计值精度更高。综合上述做法，修正RBV：

把式（13）、式（14）代人式（9），得到一个新的统计量Z1，t+1（Δ）。当 Δ →0 时，Z1，t+1（Δ）～ N（0，1）。因此，修正后的Z1，t+1（Δ）能减少市场噪音对天然气价格波动的影响，将得到更准确的样本估计结果。由于Z1，t+1（Δ）消减了交易过程造成的摩擦，也就是未融入价格的信息不会再引起跳跃，根据式（11）以及式（12），Jt+1，α、Ct+1，α趋于更加稳定。

1.4HAR-RV-CJ模型

本文引入HAR-RV模型，对不同时段的RV建立一阶自回归模型。为了研究简便，本文把交易者分为三类：日、周和月交易者,分别代表短期、中期和长期交易者。根据式（3），可算出各时段的RV。三个时段RV可定义为单时段RV之和的平均。单一时段RV定义：

其中h=1、h=5、h=22，分别表示日、周以及月RV。定义多时段 Jt，t+h和 Ct，t+h：

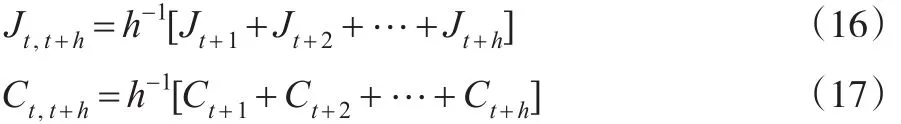
则HAR-RV-CJ模型表示为：

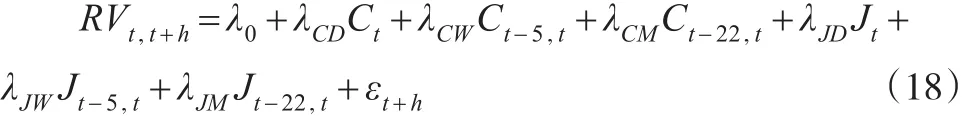
其中，λCD、λCW、λCM分别表示连续样本路径方差日、周以及月投资者的回归系数，而λJD、λJW、λJM分别表示离散跳跃方差日、周以及月投资者的回归系数。由于天然气价格收益波动率预测倾向于使用RV的标准差（RVt）1/2和对数已实现波动率 ln（RVt）计算，主要是用这两种方式计算能减少市场噪音的影响。式（18）改写成（RVt）1/2和 ln（RVt）：

模型主要反映了天然气市场价格波动是一个由不同波动成分相互叠加的复杂混合波动，是由短、中、长期投资者等交易行为共同作用的结果，其偏回归系数直接度量了特定类型交易者的行为对整个波动率的边际影响。同时，模型也很好地刻画了波动率的长记忆性特征。

2 实证

2.1 样本数据统计

天然气市场已经形成以北美、欧洲和亚太为终端的三大地区性贸易中心，分别是美国的Henry Hub、英国的NBP和日本的LNG。这三大中心天然气价格是国际天然气价格水平的重要标尺和价格涨跌的风向标。而Henry Hub交易中心是市场流动性最高、影响力最大、最能反映市场供需关系。因此，本文天然气价格数据来源于Henry Hub，采样时间从1997年1月7日至2015年1日29日。剔除了不完整的交易数据、空缺数据，得到4524个有效交易日，每个交易日产生1个数据，共计4524个价格数据。前4484个数据用作训练数据，构建RV回归模型，后40个数据用作测试数据，检验模型预测能力。

图1 天然气价格时间序列

图1是天然气价格时间序图。图1显示，天然气价格变化趋势具有强波动性、非平稳性和潜在周期性特征。第一，强波动性。从1997年初至2015年初，天然气价格超过6次大幅震荡，分别是2001年初期、2003年末期、2005年末期、2008年末期、2010年末期、2013年初期。最高价格是最低价格10倍以上。第二，潜在周期性。根据上面的分析知，天然气价格每隔2到3年就暴涨一次，而且每次大涨后紧接着大跌，表现出一定的惯性和周期性。第三，非平稳性。从1997年初到2008年中后期，天然气价格总体走势是震荡上涨；2009年开始至现在，天然气价格震荡下行。

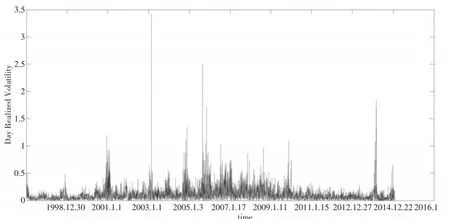
图2 天然气价格RV时间序列

图2是1997年1月7日至2015年1月29日天然气价格RV时间序列。从图2看出RV有如下特征：第一，尖峰厚尾性。表1显示，RV峰度高达314.8262，远远大于3，该序列表现为明显的尖峰厚尾性。厚尾性存在，表明天然气价格波动幅度较大；第二，右偏性。RV的偏度明显大于0，具有较高的偏度；第三，跳跃性。比较Jt与RV的均值大小可知，Jt在RV中占比较大，高达37.3%。这表明RV中，存在较大的跳跃性；第四，长记忆性。具有长记忆性的时间序列具有明显的非周期性的循环特征，即历史事件会持续影响当期的事件和未来将要发生的事件；第五，波动聚集性。一个大的价格波动率后面紧跟着一个大的价格波动，一个小的价格波动率后面紧跟着一个小的价格波动。

图3 天然气价格RV核密度分布

图3是天然气价格RV核密度估计（KDE）序列。图3显示，KDE曲线是光滑的。从位置上看，整体由左向右偏移趋势；从峰度上看，峰值逐渐右移，左端至中间部分的面积逐渐减少，右端拖尾部分越来越大，反映出天然气消费快速发展，消费趋于分散，交易量不断增长；从分布状况上看，曲线呈多峰现象，说明天然气价格RV变化是不收敛的，各时期变化不协调，同时各时期的峰值差异显著，说明天然气价格RV整体上是震荡的、非平稳的。

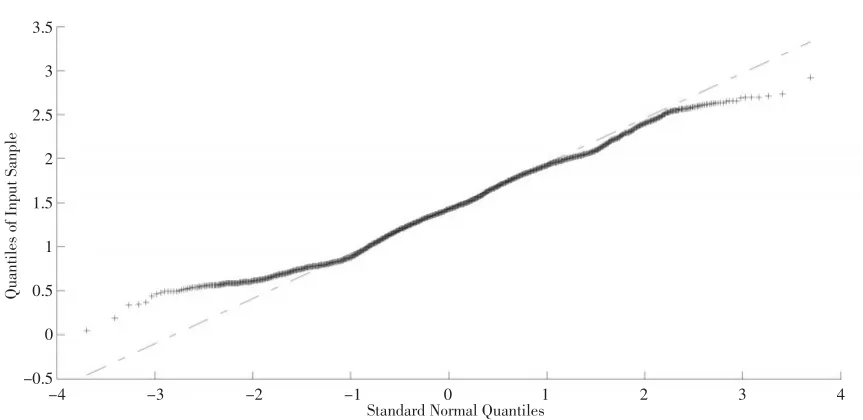
图4 天然气价格RVQ-Q分布

图4是天然气价格RV的Q-Q图。图4显示，样本曲线中间部分样本点在直线上，而左下边样本点没有下弯趋势，右上边样本点也没有上弯趋势，曲线尾部明显偏离直线，表明RV已直观显现出非正态性。

图5 天然气价格RVt时间序列

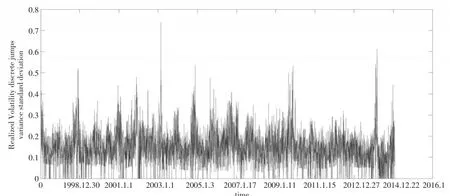
图6 天然气价格RV的时间序列

12、log（Jt+1）统计量。从表1看出：第一，log（RVt）的峰度值约等于3，变量分布接近于正态分布，具有一定的稳定性，其他波动率峰度值偏离3较远，因此，从天然气收益波动率建模的角度考虑，应该使用log（RVt）进行建模；第二，Jt的最大、最小以及中值比对应RVt的要小，说明天然气价格中离散跳跃成份在减弱，对天然气价格波动影响在减少；第三，尽管特别是）统计量LB15的值在传统置信水平上仍是显著的，但与RVt相比，Jt自相关的水平较低，说明Jt的动态相依性变弱；第四，要比连续样本路径的标准方差小，说明Jt趋于稳定；第五，与连续样本路径的方差相比，Jt的均值只占到RVt均值的37.2%，因此，Jt对价格波动影响并不十分重要。

2.2 市场噪音对Jt影响

天然气市场存在噪音，噪音影响天然气价格。表2记录了考虑市场微观结构噪音条件天然气价格Jt统计特征。其中Pp表示发生跳跃的天数占样本天数的比例；Mean和St.Dev.分别代表显著跳跃方差序列的均值和标准差；LB15，Jt，α是 Jt，α滞后15阶序列自相关的LB统计量；LB15，Dt，α是 Dt，α天然气价格 RVt发生显著跳跃的久期序列滞后15阶自相关的LB统计量；是天然气价格RVt的规模序列滞后15阶自相关的LB统计量。从天然气价格RVt发生显著跳跃的天数占样本期天数的比例发现，当显著性水平α趋大时，RVt发生显著跳跃的天数明显减少。这说明，市场微观结构噪音对天然气价格RVt的影响越小，发生跳跃的现象就越少。此外，以二次幂变差测量为理论基础构建的方法识别RVt发生显著跳跃的天数，比用连续价格过程的模型还要多。显著性水平α=0.001，以二次幂变差测量为理论基础构建的方法对天然气价格数据进行测试，发现有309天波动率发生显著跳跃，而用连续的价格过程方法测试，发现波动率发生显著跳跃的期望天数为4（为样本期天数的0.0008倍）。产生这种差异性，主要原因是与数据的频率有关。使用RVt或者低频收益数据时，损失了影响价格波动的重要信息，导致识别RVt发生跳跃的方法出现严重的误差，而使用高频价格数据RVt来识别波动是否发生跳跃，由于保留较多市场微观结构噪音的信息，不会产生这种现象。

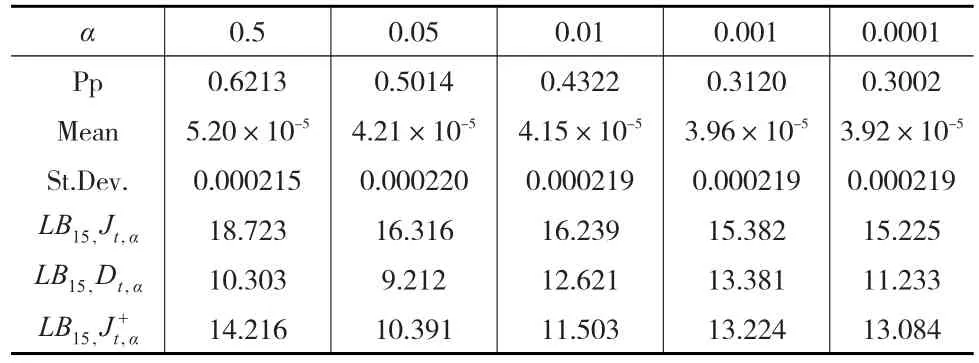
表2 市场噪音条件下Jt的统计量

表2显示，天然气价格RVt发生显著跳跃的天数依赖于α的选择。当显著性水平α大于0.5时，置信度越来越高，此时，Jt，α的样本均值和标准差是非常接近的，显示出与α的选择无关。由统计量 LB15，Jt，α的值不为0看出，Jt，α具有自相关性，原因是滞后性引起的随机误差项存在相关性，这充分表明Jt，α具有一定的可预测性。

为进一步看到天然气价格RVt跳跃特征，现将Jt，α分解为久期（duration）和规模（size）[7]。久期是指天然气价格RVt发生显著跳跃间隔的天数，而规模是指天然气价格RVt发生显著跳跃方差序列中剔除零值后得到的数据。表2 显 示 ，当 显 著 性 α =0.001 时 ，统 计 量 LB15，Dt，α和的值不为0，说明天然气价格日 RVt发生显著跳跃的久期和规模都具有自相关的特征，表明Jt，α具有明显聚集效应特征。图6显示变化趋势也具有聚集效应特征，这进一步说明聚集效应是天然气价格Jt，α的特征。

2.3 基于HAR-RV-CJ模型的RV预测

为进一步探究Ct和Jt对RVt的影响差异性，将天然气价格RVt分解为Ct和Jt。取置信度β=0.999，在下面的符号中，如 Jt，0.999和 Ct，0.999均略去了0.999下标。

HAR-RV-CJ模型对训练集数据进行回归分析，参数估计值及样本内诊断结果由表3给出。第一，所有HAR-RV-CJ模型回归结果，包括日、周和月，离散跳跃方差估计系数t检验值都是不显著的（括号中的数值是t检验值），这说明了自变量Jt对因变量RVt的预测影响不大；另一方面，也说明了RVt的可预测性主要依赖Ct，这一点可以从Ct的λCD、λCW、λCM估计系数的t检验值均大于0.999来证实；第二，无论是日、周、月时段，log（RVt，t+h）模型回归常数项均小于0，说明其具有滞后性。第三，和 log（RVt，t+h）的拟合优度的值明显大于已实现波动率的，这说明，这两项能够获得更高的预测精度。以天然气价格RVt预测为例，使用RVt的拟合优度仅为0.043，而使用已实现波动率的标准差拟合优度上升至0.226，使用对数已实现波动率拟合优度最高，达到0.305。因此，在天然气交易实践中使用 log（RVt，t+h）进行建模和预测效果会更好。

表3 HAR-RV-CJ模型回归参数

根据表3的回归系数，分别构建h=1,5,22时的HAR-RV-CJ模型：

HAR-RV-CJ模型调用2014年12月2日至2015年1月29日40个交日天然气价格数据，预测天然气价格RVt。根据预测值与实际值，按公式算三时段的均方根误差，其中表示RV的预测值。计算得到 RMSEh=1=0.0106，RMSEh=5=0.0225，RMSEh=22=0.0301。与RV拟合曲线图显示：第一，与RV拟tt合程度高；第二，当h=1时，RMSE最小，说明与RV拟t合效果最好，而h=5,22时，拟合效果依次减弱，这进一步说明取样频率越高，预测值与实际值拟合精度越高；第三，HAR-RV-CJ模型能很好地预测天然气价格日、周以及月的RVt；第四，HAR-RV-CJ模型为研究天然气价格走势提供较好方法。这为进一步预测未来天然气价格变化趋势提供了有效的方法。

3 结论

天然气市场存在异质性，导致天然气价格由非供求关系引发波动。为了探讨天然气价格变化趋势，本文首先介绍了一种识别天然气价格日已实现波动率发生跳跃的方法，将日已实现波动率分解为连续样本路径方差和离散跳跃方差，进而研究了离散跳跃方差序列的统计特征；其次，结合天然气市场上交易者及交易时间特点，构建了HAR-RV-CJ模型；最后用该模型对1997年1月7日至2015年1月29日的天然气价格数据进行实证分析。研究结果表明：

（1）天然气价格RVt存在尖峰厚尾性、右偏性、跳跃性、长记忆性以及波动聚集性等特征，研究还发现RVt不符合正态分布。天然气价格RVt发生显著跳跃的比例是相当高的，达到37.3%；但是当显著性水平α大于0.5时，RVt发生显著跳跃特征与α的选取无关。

（2）天然气价格RVt的离散跳跃方差序列不仅具有自相关性，而且具有聚集效应和可预测性，但是跳跃对价格波动影响并不十分重要。连续样本路径方差序列是天然气价格RVt预测的主要决定因素，离散跳跃方差序列对RVt的预测影响不大。

（3）RVt的标准差和 log（RVt，t+h）模型能很好预测日、周和月的RVt。多时段的HAR-RV-CJ模型能够较好预测较长时期的天然气价格的波动率，当然在天然气交易实践中使用log（RVt，t+h）进行建模和预测效果会更好。

[1]Andersen T G,Bollerslev T.Answering the Skeptics:Yes，Standard Volatility Models do Provide Accurate Forecasts[J].International Eco⁃nomic Review,1998,39（6）.

[2]Barndorff-Nielsen O,Shephard N.Econometrics Analysis of Realized Volatility and Its Use in Estimating Stochastic Volatility Models[J].Journal of the Royal Statistical Society,2002,64（8）.

[3]Barndorff-Nielsen O,Shephard N.Power and Bi-power Variation With Stochastic Volatility and Jumps[J].J.Finance.Econ,2004,2（3）.

[4]Andersen T G,Bollerslev T,Hung X.A Reduced Form Frame-work for Modeling Volatility of Speculative Prices Based on Realized Varia⁃tion Measures[J].Journal of Econometrics,2011,169（9）.

[5]Zhang L,Mykland P A，Aït-Sahalia,Y.A Tale of Two Time Scales:Determining Integrated Volatility With Noisy High Frequency Data[J].J.Am.Stat.Assoc,2005，6 （7）.

[6]Andersen T G,Dobrev D,Schaumburg E.Jump-robust Volatility Esti⁃mation Using Nearest Neighbor Truncation[J].J.Econ,2012,16（9）.

[7]Huang X,Tauchen G.The Relative Price Contribution of Jumps to To⁃tal Price Variance[J].J.Financ.Econ,2005,3（6）.