适配功率电机齿槽转矩削弱方法研究*
2018-01-05关玉明刘纯祥
李 曾, 关玉明, 刘纯祥, 赵 越, 李 军
(1. 河北工业大学 机械工程学院,天津 300000; 2. 唐山学院 机电工程系,河北 唐山 063000)
适配功率电机齿槽转矩削弱方法研究*
李 曾1, 关玉明1, 刘纯祥2, 赵 越1, 李 军1
(1. 河北工业大学 机械工程学院,天津 300000; 2. 唐山学院 机电工程系,河北 唐山 063000)
为削弱适配功率电机齿槽转矩,提高该电机动力输出性能,提出了匹配相邻磁极极弧系数的方法。首先,运用麦克斯韦应力张量法和傅里叶分解求解适配功率电机齿槽转矩解析模型,并对不等极弧系数进行匹配组合,解析结果表明齿槽转矩削弱了35%左右。然后,采用全局优化算法对不等极弧系数进行全局寻优匹配,齿槽转矩进一步得到优化。最后,依据理论研究结果加工制作样机并进行试验,试验结果显示,齿槽转矩实测数据和优化结果相比,总体误差为5%左右,且整体趋势与优化曲线相符。因此,所提用于削弱适配功率电机齿槽转矩的方法是有效且可行的。
适配功率电机;齿槽转矩;削弱方法;样机试验
0 引 言
适配功率电机是在永磁有刷直流电机的基础上创新研发的、可输出两种电磁功率的电动汽车用新型驱动电机。该电机主要适用于城市重载电动汽车[1]。适配功率电机作为永磁电机的一种,其有槽电枢铁心与永磁体磁场相互作用产生圆周方向上的齿槽转矩[2-3]。齿槽转矩作用于适配功率电机时产生噪声和振动,进而影响适配功率电机的使用寿命,降低了城市重载电动汽车的行驶平稳性和乘坐舒适程度,因此,精确计算并有效削弱齿槽转矩对提高适配功率电机输出性能具有重要意义。相关文献对齿槽转矩计算方法和削弱措施进行了研究。文献[4]在研究中忽略了电枢槽的存在,将电枢铁心视为无槽圆轴,该近似处理对齿槽转矩的计算结果带来误差。文献[5]通过偏转磁极相对位置来削弱齿槽转矩,研究理论过于复杂,同时在该文献中没有给出通用的研究方法,因此其研究理论适用范围受到限制。文献[6]虽然采用不等极弧系数匹配解析研究削弱齿槽转矩,但没有进行深入分析,优化结果不明显。
在现有文献对永磁电机齿槽转矩研究的基础上,本文提出了运用麦克斯韦应力张量法求解适配功率电机齿槽转矩解析模型,并运用不等极弧系数匹配选优的方法,对完成傅里叶分解的齿槽转矩解析式进行解析分析,匹配适当的相邻磁极极弧系数,对齿槽转矩的削弱起到一定的效果。为了进一步优化相邻极弧系数的选择,本文将遗传算法和有限元法相结合,对极弧系数的匹配进行全局寻优,以更有效地削弱齿槽转矩。最后,通过电动汽车用电机试验平台对适配功率电机样机进行试验,测定齿槽转矩相关数据并进行数据处理,验证上述理论研究的正确性。
1 基于不等极弧系数匹配的齿槽转矩分析
1. 1 齿槽转矩的解析模型
运用麦克斯韦应力张量法计算齿槽转矩,首先要对适配功率电机的气隙磁场进行解析分析[7]。适配功率电机相关尺寸参数示意图如图1所示。
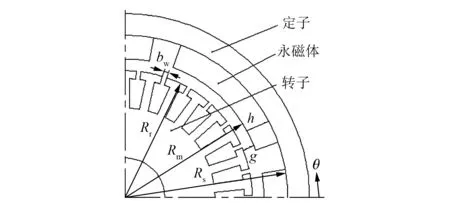
图1 参数示意图
图1中相关尺寸参数说明:Rr为转子外径;Rm为磁极内径;Rs为定子内径;bw为电枢槽槽口宽;h为永磁体径向厚度;g为气隙宽度;θ为机械角度。
解析法分析适配功率电机气隙磁场,求解气隙磁通密度。为简化解析模型,假设铁心材料磁导率为无限大,磁极径向磁化并均匀充磁,忽略转子偏心影响,气隙磁场沿适配功率电机轴向均匀分布,即可在二维平面内解析分析[8-9]。首先视转子为光滑圆柱铁心结构,即先忽略转子电枢槽的影响,则磁通密度矢量B和磁场强度矢量H在气隙磁场和永磁体磁场存在如下关系[10]:
(1)
式中:Ba——气隙磁场磁通密度矢量;
Bp——永磁体磁通密度矢量;
μ0——真空磁导率,μ0=4π×10-7H/m;
μr——永磁体相对磁导率;
Ha——气隙磁场强度矢量;
Hp——永磁体磁场强度矢量;
M——永磁体磁化强度矢量。
在极坐标下,永磁体磁化强度矢量M可表示为
M=Mrr+Mθθ(2)
式中:Mr和Mθ——永磁体磁化强度的径向和切向分量。
对Mr和Mθ分别进行傅里叶展开[11]:
(3)
式中:Br——永磁体剩余磁通密度,M=Br/μ0;
αr——极弧系数;
p——永磁体磁极极对数。
另外,磁标势在气隙的分布遵循拉普拉斯方程:
(4)
磁标势在永磁体区域的分布遵循准泊松方程[12]:
(5)
式中:φa——气隙磁标势;
φp——永磁体磁标势。
根据磁标势和磁场强度的关系,结合电机磁场边界条件,由式(1)~式(5)计算得到适配功率电机气隙磁场分布的解析式如下[13]:
(6)
式中:Bar——径向气隙磁通密度;
Baθ——切向气隙磁通密度。
K=
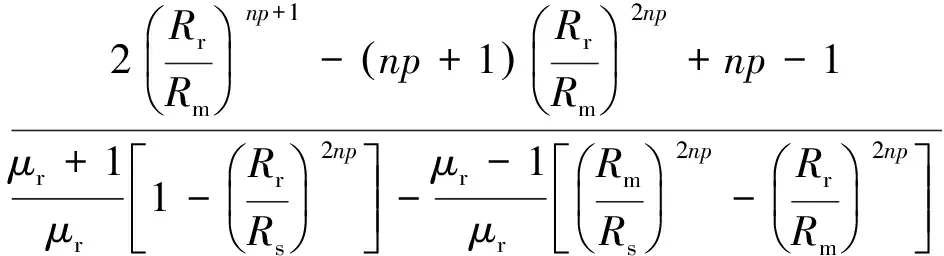
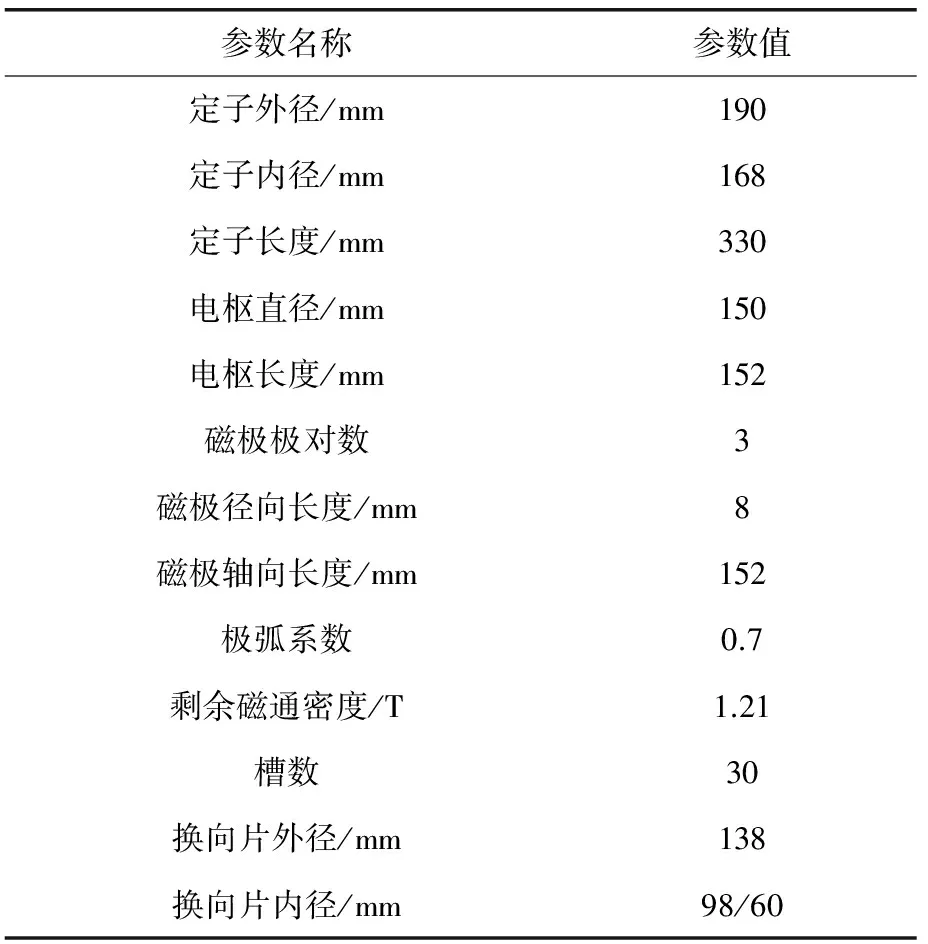
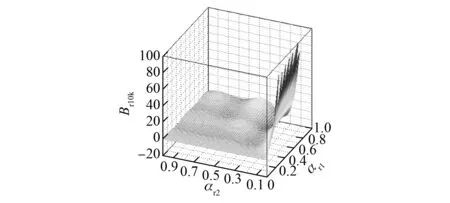
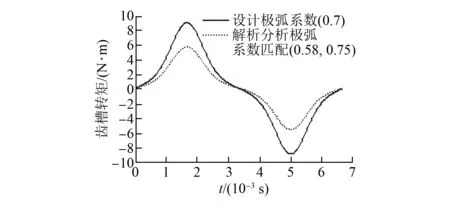
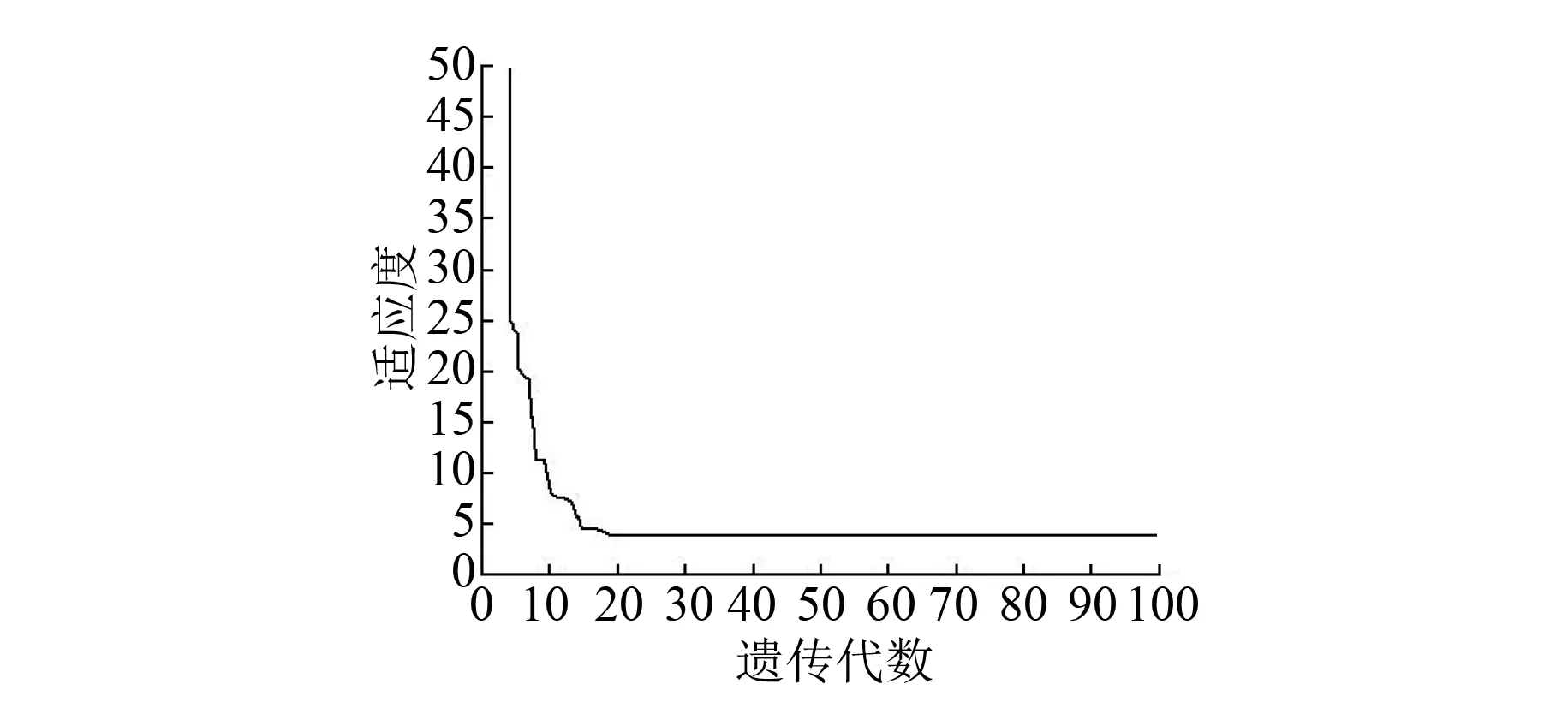
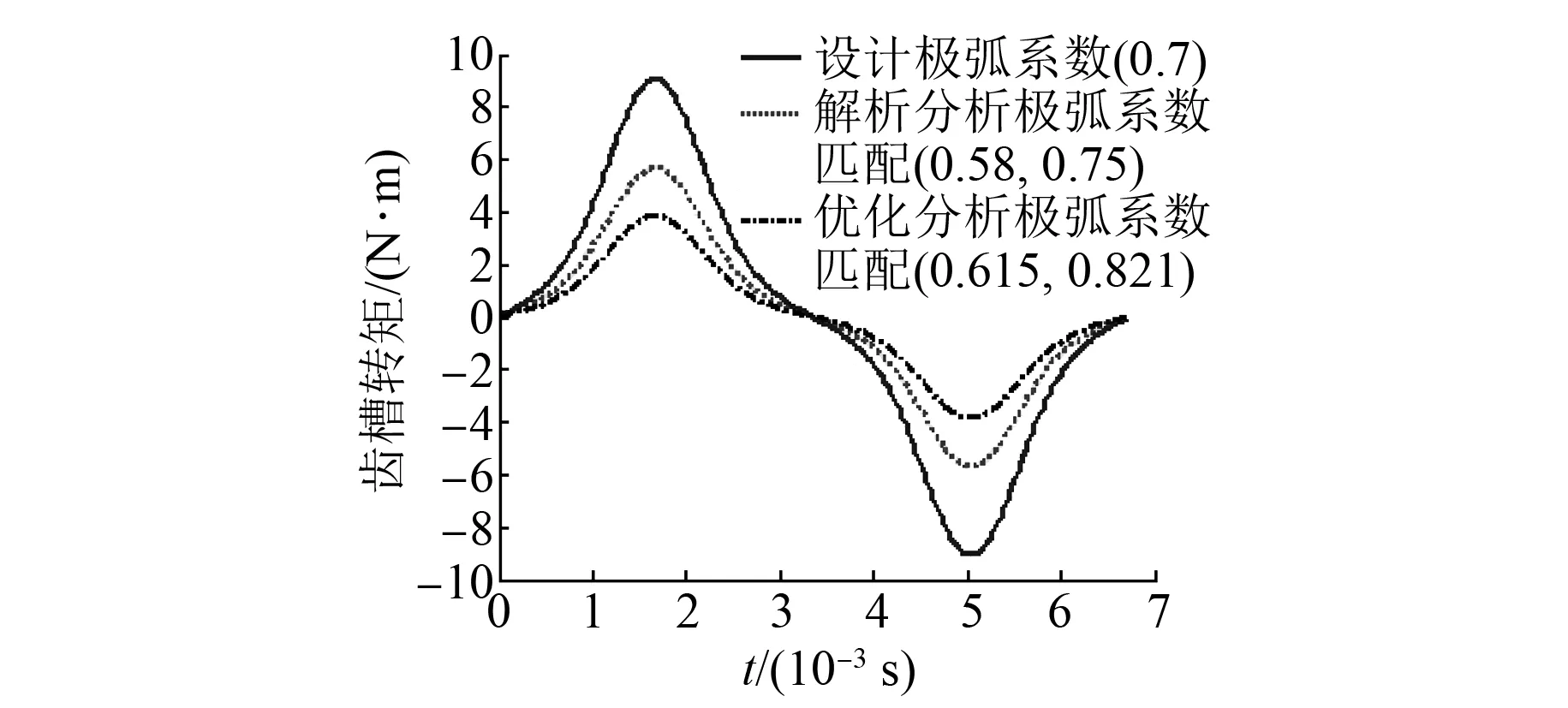
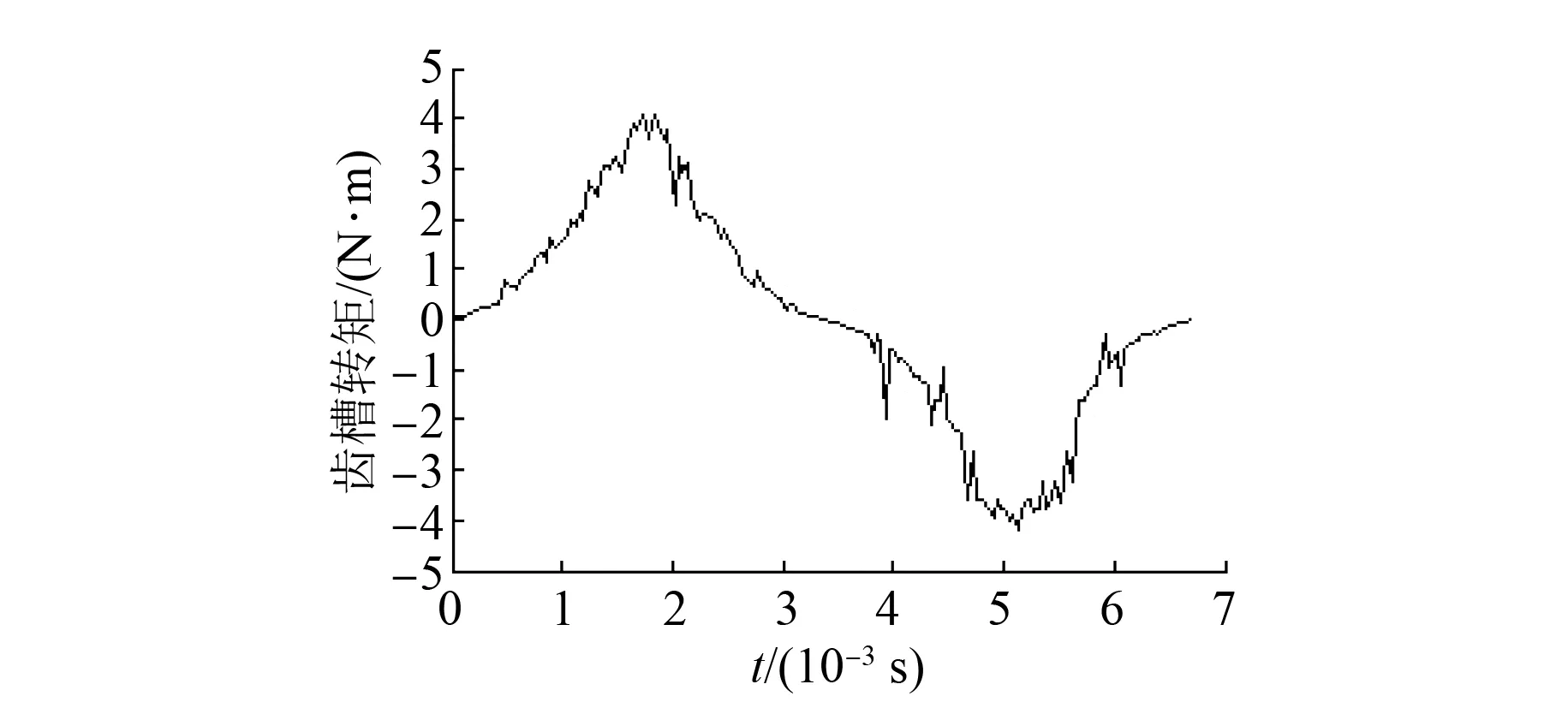
Rr (9) 式中:Barλ——考虑电枢槽影响的径向气隙磁通密度; Baθλ——考虑电枢槽影响的切向气隙磁通密度。 (10) 式中:Z——电枢齿数; ω——角速度; (11) 式中:τt——转子齿距,τt=2πRr/Z; β——与自变量参数r相关的系数。 (12) 式中:θa、θb——机械角度值。 在极坐标下,应用麦克斯韦应力张量法[17]解得电枢齿j的电磁转矩为 式中:ls——定子轴向有效长度; j=1,2,3,…,Z。 由叠加法得到适配功率电机的齿槽转矩为 (14) 式(14)可较精确求得适配功率电机的齿槽转矩,为研究该电机齿槽转矩的削弱方法奠定了基础,同时上述齿槽转矩解析模型也可作为电机设计过程中的计算依据[18]。 现有永磁电机磁极结构一般都是相同的。现通过改变适配功率电机磁极的极弧系数,对磁极的结构尺寸进行优化。对相邻不同结构磁极的极弧系数合理选择,有效地削弱适配功率电机的齿槽转矩[19]。从式(6)可以看出剩余磁通密度Br对齿槽转矩有较大的影响,采用不等极弧系数匹配时,对剩余磁通密度Br进行傅里叶展开,表达式为 (15) 其中: (16) αr1和αr2分别为相邻磁极的极弧系数。 (18) 磁场能量We的表达式[20]: (19) 式中:La——电枢轴向长度; α——定转子相对位置角; Gm——与α无关的系数。 由式(19)可知,对于式(17),只有mZ/p次傅里叶系数对齿槽转矩有影响,且取决于适配功率电机的槽数(齿数)和极数。适配功率电机结构设计参数如表1所示。 表1 电机结构参数 由上可知,对适配功率电机齿槽转矩起作用的是10k(k为整数)次傅里叶系数。为使齿槽转矩取最小值,应使Br10k趋于零,即 对式(20)进行数据处理,得到随αr1和αr2变化而改变的傅里叶系数Br10k立体图,如图2所示。 图2 傅里叶系数Br10k立体图 从图2可知,随着αr1和αr2的变化,傅里叶系数Br10k的图像在整体上呈现出上下波动,且局部范围的波动量较大,因此通过求解傅里叶系数Br10k的最小值来削弱适配功率电机的齿槽转矩是有意义的。另外,从图2中可以知道该立体图是基于傅里叶系数Br10k为零的基准面上下波动的,验证了上述理论分析的可行性,存在使式(20)为零的αr1和αr2的匹配组合。在数据中提取图2全部可能的αr1和αr2的匹配点,构成适配功率电机极弧系数匹配图,如图3所示。 图3 极弧系数匹配图 图4 极弧系数匹配的齿槽转矩削弱对比 图3体现了适配功率电机极弧系数匹配的所有可能,根据该电机在结构设计中所设定的极弧系数α0=0.7及极弧系数在永磁电机设计中的一般取值范围[21],设定了该电机极弧系数匹配的选择范围,如图3中的圆形范围所示。根据图3选取(0.58,0.75)进行匹配,由上述齿槽转矩的计算解析式对数据进行处理,得到齿槽转矩对比图,如图4所示。 通过图4设计极弧系数所求得的齿槽转矩与解析分析极弧系数匹配所求得的齿槽转矩相对比,可以看出解析分析极弧系数匹配所求得的齿槽转矩得到明显的削弱。从图4中可以看出,解析优化后的齿槽转矩峰值为5.85 N·m,与解析优化前的峰值(9.16 N·m)相比,削弱了36.14%。同时,解析优化后的齿槽转矩曲线整体上下波动相对减弱,过渡平缓,有效降低了适配功率电机输出转矩脉动及整体振动。 由于解析优化没有考虑适配功率电机在实际工作过程中的影响因素,所以得到的极弧系数匹配不能保证齿槽转矩削弱最多。为使齿槽转矩最小、适配功率电机表现更优越的动力性能,本文进一步采用全局优化算法对齿槽转矩进行研究,选出更理想的极弧系数匹配组合。 图5 GA流程图 遗传算法(Genetic Algorithm,GA)是模拟自然界生物进化机制,由生物进化过程的自组织、自适应随机搜索而形成的一种全局寻优算法。GA具有全局寻优能力强、群体展开搜索不易陷入局部最优等特点,可知GA适用于求解该电机极弧系数的最佳匹配问题。GA计算流程图如图5所示[22〗。 取种群规模为40,交叉概率为0.7,变异概率为0.1,遗传代数为100代,运用MATLAB软件运行GA程序得到某次运算结果,如图6所示。 图6 适应度变化曲线 图6反映出在优化过程中种群最优个体适应度值的整体变化情况。在最后,种群最优个体适应度趋于恒定,则认为此时已经找到最优结果,运算可以结束。在本次运算中得到的最优个体适应度值为3.921 6,最优个体为(0.614 7,0.821 3)。因此,经过GA优化得到的不等极弧系数匹配结果为(0.615,0.821)。将该优化结果代入上述解析式,进行数据处理得到适配功率电机齿槽转矩对比图,如图7所示。 图7 极弧系数匹配优化的齿槽转矩削弱对比 由图7可知,通过GA对不等极弧系数匹配进行选优,适配功率电机齿槽转矩进一步得到削弱,同时得到了最优的相邻磁极极弧系数匹配,为适配功率电机结构设计提供了更优的结构参数。可以看出,不仅齿槽转矩的幅值在整体上减小了,而且在一个周期内齿槽转矩的整体走势更加平缓,有利于该电机平稳转动,降低了城市重载电动汽车的振动与噪声。另外需要指出的是,该优化结果所求得的齿槽转矩峰值为3.91 N·m,与GA得到的结果(3.921 6)基本一致,验证了该优化算法的有效性;同时与解析优化后的齿槽转矩峰值(5.85 N·m)相比,再次削弱了33.16%。因此,采用不等极弧系数匹配的理论对适配功率电机齿槽转矩进行削弱是可行的。 根据极弧系数的最终优化结果及适配功率电机相关结构设计参数,制作适配功率电机样机。 为测定适配功率电机齿槽转矩变化图,搭建适配功率电机试验平台如图8所示。试验平台设备主要包括:适配功率电机样机、直流电源、模拟电动汽车制动装置、电动汽车电机测试系统、测功机、扭矩传感器、样机控制器、计算机数据处理系统等。 图8 适配功率电机试验平台 调整试验系统使样机运行在300 r/min,记录相关输入和输出数据,进行数据处理,绘制适配功率电机样机齿槽转矩实测图,如图9所示。 图9 齿槽转矩实测曲线 图9给出了当适配功率电机拖负载转动时其齿槽转矩的变化情况,与经过极弧系数匹配优化后所求得的齿槽转矩变化曲线大体相符,例证了本文理论研究的正确性,说明利用不等极弧系数匹配的方法研究削弱齿槽转矩是有效的,也说明运用GA对极弧系数匹配进行全局优化能够进一步减小齿槽转矩的幅值,降低动力系统振动。在图9中得到适配功率电机样机的实际齿槽转矩峰值为4.08 N·m,相比于优化后齿槽转矩峰值(3.91 N·m)误差约在4%,同时齿槽转矩实测曲线呈现出较多的突变和波动,这是由适配功率电机样机试验中机械摩擦、换向损耗、电枢反应等原因造成的。 在现有研究水平的基础上,本文用解析法对适配功率电机科研项目的齿槽转矩进行研究,提出了利用相邻磁极极弧系数匹配组合来削弱该电机齿槽转矩的方法,并通过解析模型进行数据处理,证明了该方法的可行性。在此前提下,运用优化算法对不等极弧系数进行全局寻优组合,解析数据表明齿槽转矩进一步得到削弱。最后,样机试验所得齿槽转矩实测曲线与优化后齿槽转矩变化曲线基本一致,即在本文理论研究的指导下,所加工样机的齿槽转矩指标符合理论研究标准。 根据上述结论可知,本文对适配功率电机齿槽转矩的研究方法是可行且比较成功的,同时也为永磁电机齿槽转矩方面的研究提供了必要的技术与数据支持。 [1] 关玉明,王锡瑞,燕唐,等.城市重载电动汽车适配功率电机可行性研究[J].中国机械工程,2016,27(19): 2687-2692. [2] 黄守道,刘婷,欧阳红林,等.基于槽口偏移的永磁电机齿槽转矩削弱方法[J].电工技术学报,2013,28(3): 99-106. [3] 王晓远,贾旭.基于槽口优化的电动汽车用大功率无刷直流电机齿槽转矩削弱方法[J].电工技术学报,2013,28(6): 40-45. [4] 冀溥,王秀和,王道涵,等.转子静态偏心的表面式永磁电机齿槽转矩研究[J].中国电机工程学报,2004,24(9): 188-191. [5] TOUZHU L, GORDON S. Reduction of cogging torque in permanent magnet motors[J].IEEE Transactions on Magnetics,1988,24(6): 2901-2903. [6] BIANCHI N, BOLOGNANI S. Design techniques for reducing the cogging torque in surface-mounted PM motors[J].IEEE Transactions on Industry Applications,2002,85(5): 1259-1265. [7] HE G, HUANG Z, QIN R, et al. Numerical prediction of electromagnetic vibration and noise of permanent-magnet direct current commutator motors with rotor eccentricities and glue effects[J].IEEE Transactions on Magnetics,2012,48(5): 1924-1931. [8] HE G, HUANG Z, CHEN D. Two-dimensional field analysis on electromagnetic vibration-and-noise sources in permanent-magnet direct current commutator motors[J].IEEE Transactions on Magnetics,2011,47(4): 787-794. [9] 仇志坚,李琛,周晓燕,等.表贴式永磁电机转子偏心空载气隙磁场解析[J].电工技术学报,2013,28(3): 114-121. [10] 张冉,王秀和.基于等效剩磁法的永磁电动机转子偏心磁场解析计算[J].电工技术学报,2009,24(5): 7-12. [11] WILLIAM H H.工程电磁学[M].徐安士,周乐柱,译.北京:电子工业出版社,2004. [12] ZHU Z Q, DAVID H, CHAN C C, et al. Improved analytical model for predicting the magnetic field distribution in brushless permanent-magnet machines[J].IEEE Transactions on Magnetics,2002,38(1): 229-238. [13] ZHU Z Q, DAVID H, EKKEHARD B, et al. Instantaneous magnetic field distribution in brushless permanent magnet dc motors, part I: open-circuit field[J].IEEE Transactions on Magnetics,1993,29(1): 124-135. [14] ZHU Z Q, HOWE D. Instantaneous magnetic field distribution in brushless permanent magnet dc motors, part III: effect of stator slotting[J].IEEE Transactions on Magnetics,1993,29(1): 143-151. [15] ZHU S Z, JIANG S Z, ZHU Z Q, et al. Comparison of alternate analytical models for predicting cogging torque in surface-mounted permanent magnet machines[C]∥ IEEE Vehicle Power and Propulsion Conference,China,Harbin,2008: 1-6. [16] ZHU Z Q, HOWE D. Instantaneous magnetic field distribution in permanent magnet brushless dc motors, part IV: magnetic field on load[J].IEEE Transactions on Magnetics,1993,29(1): 152-158. [17] HE G, HUANG Z, CHEN D. Two-dimensional field analysis on electromagnetic vibration-and-noise sources in permanent-magnet direct current commutator motors[J].IEEE Transactions on Magnetics,2011,47(4): 787-794. [18] ZHU Z Q, HOWE D. Analytical prediction of the cogging torque in radial-field permanent magnet brushless motors[J].Magnetics IEEE Transactions on,1992,28(2): 1371-1374. [19] WANG X, DING T, SHEN N, et al. Optimization of the different pole arc combination to reduce the cogging torque in PMDC motors[C]∥ Biennial IEEE Conference on Electromagnetic Field Computation IEEE,2006: 367-367. [20] WANG X, YANG Y, FU D. Study of cogging torque in surface-mounted permanent magnet motors with energy method[J].Journal of Magnetism & Magnetic Materials,2003,267(1): 80-85. [21] 黄国治,傅丰礼.中小旋转电机设计手册[M].北京:中国电力出版社,2014. [22] FAZLIPOUR Z, KIANINEZHAD R, RAZAZ M. Genetic algorithm based design optimization of a six phase induction motor[J].Journal of Electrical Engineering & Technology,2015,10(3): 1007-1014. StudyontheMethodtoReducetheCoggingTorqueofPowerAdaptiveMotor* LIZeng1,GUANYuming1,LIUChunxiang2,ZHAOYue1,LIJun1 (1. School of Mechanical Engineering, Hebei University of Technology, Tianjin 300000, China;2. Department of Electrical and Mechanical Engineering, Tangshan University, Tangshan 063000, China) In order to reduce the cogging torque, improve the motor power output performance, put forward a method of matching pole arc coefficient of the adjacent pole. Used the Maxwell stress tensor method and Fourier decomposition solve the cogging torque analytical model of the power adaptive motor, and combined the different pole arc coefficients, analysis results showed that the reducing of cogging torque was about 35%. Then, unequal pole arc coefficients were globally optimized by the global optimization algorithm, showed that the cogging torque was further optimized. Finally, the prototype was produced on the basis of the results of theoretical research and given a prototype test, the results showed that: compared to the cogging torque measured data and the results of optimization, the overall error was about 5%, and the overall trend curve matches the optimization. Therefore, in this paper the method of weakening cogging torque of the power adaptive motor was effective and feasible. poweradaptivemotor;coggingtorque;weakeningmethod;prototypetest 国家自然科学基金项目(51605135);天津市科技特派员项目(14JCTPJC00532);河北省科技计划项目(15211829) 李 曾(1989—),男,硕士研究生,研究方向为城市重载电动汽车用适配功率电机及其控制、电机试验。 关玉明(1957—),男,硕士,教授,博士生导师,研究方向为机电一体化成套设备研究及EV电驱动总成技术课题研究。 TM 302 A 1673-6540(2017)12- 0074- 07 2017 -05 -03
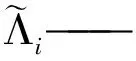
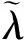
1. 2 不等极弧系数匹配解析确定


1. 3 基于优化算法的不等极弧系数匹配优化

2 试 验

3 结 语
