例谈高考中的含参问题

☉宁夏银川二中 马丽欣

例谈高考中的含参问题

☉宁夏银川二中 马丽欣

含参问题是近几年高考中的热点，也是重点.此类试题考查的知识点综合度比较高，难度比较大.下面笔者通过自己的教学实践，谈谈高考对含参问题的考查，以抛砖引玉.

一、运用单调性解决含参问题

有的题目利用洛必达法则解决比较简便，我们先介绍一下洛必达法则：

对-∞＜a＜b＜+∞，设（fx）和g（x）是两个实数值函数，并都在［a，b］上连续，在（a，b）上可微且在（a，b）上g′（x）≠0，如果在（a，b）上递增（递减），那么函数F（x）=和也在（a，b）上递增（递减）.而且，如果的单调性是严格的，那么F（x）和G（x）的单调性也是严格的.

证明：只需证明F（x）的情形，G（x）同理可得.不妨设在（a，b）上递增，g（′x）在（a，b）恒小于零.

由柯西中值定理可知，对于任意的x∈（a，b），总存在y∈（a，x），使得：

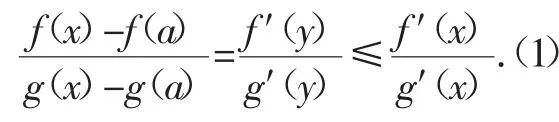
由于g′（x）＜0，x∈（a，b），故有g（x）-g（a）＜0，且［g（x）-g（a）］g（′x）＞0（.2）

在（1）式两端同时乘以（2）式，有：

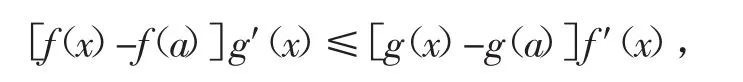
例1设函数（fx）=ln（x+1）+a（x2-x），其中a∈R.

（1）略；

（2）若∀x＞0，（fx）≥0成立，求a的取值范围.

解：对成立，等价于

从而F（x）也在（1，+∞）上单调递增，

所以有a≥0.

二、通过分类讨论确定参数的取值范围

例2设函数（fx）=ln（x+1）+a（x2-x），其中a∈R.

（1）讨论函数（fx）极值点的个数，并说明理由；

（2）若∀x＞0，（fx）≥0成立，求a的取值范围.

分析：本题是一道函数与导数的综合问题，有一定的难度和较好的区分度.第（1）问属于求函数极值问题，通过导数研究函数单调性，很好地考查了考生分类讨论思想在解题中的应用，虽然求解比较烦琐，但大多数考生都能接受，属于常规题.具体解法略.当时，（fx）的无极值点；当a＜0时，（fx）有一个极值点；当时，（fx）的有两个极值点.

此问实际上是恒成立中的参数取值问题，为了帮助同学们解决此类问题，下面将从不同视角进行求解.

解法1：由（1）可知，①当时，（fx）在（0，+∞）单调递增，而（f0）=0，则当x∈（0，+∞）时，（fx）＞0，符合题意；

③当a＞1时，g（0）＜0，x2＞0，所以函数（fx）在（0，x2）单调递减，而（f0）=0，则当x∈（0，x2）时，（fx）＜0，不符合题意；

④当a＜0时，设h（x）=x-ln（x+1），当x∈（0，+∞）时，在（0，+∞）单调递增，因此，当x∈（0，+∞）时，h（x）＞h（0）=0，ln（x+1）＜0，于是，（fx）＜x+a（x2-x）=ax2+（1-a）x，当时，ax2+（1-a）x＜0，此时f（x）＜0，不符合题意.

综上所述，a的取值范围是0≤a≤1.

本解法主要从研究函数的单调性入手，考生通常出错在分类讨论的情况较为复杂时，思路上不够十分清晰、条理，造成思维混乱，难以抽身.

三、通过分离参数确定参数取值范围

分离参数法是求解参数取值的比较常见的方法之一，对于例2的求解当然也可以利用此法，但本题的在于巧妙用上教材中习题的一个结论（∀x＞0，均有ln（x+1）＜x成立）方可使得问题得以顺利求解.

解法2：设函数（fx）=ln（x+1）+a（x2-x），∀x＞0，都有（fx）≥0成立，即ln（x+1）+a（x2-x）≥0.

由于∀x＞0均有ln（x+1）＜x成立，其证明如下：

当x＞0时，h（′x）＜0，h（x）单调递减，h（x）＜0，ln（x+1）-x＜0，即ln（x+1）＜x.

①当x=1时，ln2≥0恒成立；

综上可知，对于∀x＞0，都有（fx）≥0成立，只需0≤a≤1即可，故所求a的取值范围是0≤a≤1.

本解法主要借助分离参数法进行求解，众多考生都能想到这一求解办法，但都是因为分离参数后所得到的函数较为复杂，直接利用函数导数求解甚是复杂，于是无从研究其单调性和确定所求参数取值范围，进而望而生叹.又如下面的试题：

例3 设函数f（x）=ax-2x+2对于满足1＜x＜4的一切x都有（fx）＞0，求实数a的取值范围.

分析：此题中只含有一个参数a，属于恒成立问题.如果从二次函数的角度考虑，需要对参数a进行分情况讨论，结果就很麻烦.如果将参数a进行分离，则变为求已知函数的最值问题，就比较好办.

解：由ax-2x+2＞0，得则

当x∈（1，2）时，g′（x）＞0，g（x）是单调递增的；

当x∈（2，4）时，g′（x）＜0，g（x）是单调递减的.所以，当x=2时，g（x）有极大值

四、利用线性规划解决参数取值范围问题

例4 在平面直角坐标系xOy中，设A，B，C是圆x2+y2=1上的相异三点，若存在正实数λ，μ使得向量则λ2+（μ-3）2的取值范围是_______.

分析：此题中A，B，C是三个动点，结果含有两个参数正实数λ，μ，若以λ为横坐标，μ为纵坐标，则所求结果为点（λ，μ）到点（0，3）的距离的平方可能取到的范围.

解：平方后可得到—

即1=λ2+μ2+2λμcosθ.设θ是向量OA与OB的夹角，则θ∈（0，π）.

以λ为横坐标，μ为纵坐标，可以表示出满足上述条件的平面区域，即可行域.

确定区域内的点到（0，3）的距离的平方可能取到的范围：点（0，3）到直线λ-μ+1=0的距离为最小值，

所以，λ2+（μ-3）2的取值范围是（2，+∞）.

五、利用求导法解一类求参数取值范围

有些求参数的取值范围的问题是比较复杂的，涉及分类谈论思想，往往利用求导解决相对比较简便，进而得到参数的取值范围.

例5设函数，若对所有的x≥0，都有（fx）≤ax，求实数a的取值范围.

解 ：设，所以

例6设函数（fx）=ex+sinx-1-2x-ax2，若当x≥0时，（fx）≥0恒成立，求a的取值范围.

解：可得f（′x）=ex+cosx-2-2ax，f（″x）=ex-sinx-2a，

用两次求导及不等式x＞sinx，ex≥x+1（x≥0）可证所以当时，（fx）≥0（x≥0）成立.

通过以上几个例题可以看出，在解决含有参数的问题时，可以根据题目中所含参数的个数来选择解题方法，有时能够达到事半功倍的效果.当然，什么问题都不是绝对的，这就要求我们遇到数学问题时，要具体问题具体分析，要注意挖掘数学知识间的内在联系，同时，要善于总结、归纳，注重提炼方法.只有这样我们才能更好地学好数学.