高中数学习题课开展探究性学习的实践性思考

☉江苏省苏州市吴江汾湖高级中学 卢 平

高中数学习题课开展探究性学习的实践性思考

☉江苏省苏州市吴江汾湖高级中学 卢 平

数学教师在课堂教学这一主阵地上如果只是专注于知识的呈现、识记、阐释及理解，数学课堂教学的功能因为数学思考及研究方法的感悟不够而被无形降低.不过，教师如果能够在教学中精心设计教学活动的推进并注重培养学生的思考，学生的认识力往往能够在这样有意义的过程中得到有效的锻炼和提高.因此，那些能够给予学生足够时间与空间进行观察、实验、猜想、验证、推理、计算及证明的各种数学活动是非常有必要的，学生对概念的理解、数学知识技能及思想方法的掌握往往会在这些有意义的活动中得以实现.

近年来，各地在课程教学改革的研究中均把探究性学习进行课堂教学重构作为研究的重点，探究性学习成为了变革学习方式最为主要的手段.事实上，丰富并改进学生的学习方式确实已经成为我国基础教育课程改革的基本理念之一，课程标准也明确了高中数学课程应该着力倡导学生的自主探索、动手实践、合作交流及阅读自学等，那些局限于知识的接受、记忆、模仿以及练习的学习活动应该得到有力的整改，使得那些有助于发挥学生学习主动性的方式最大程度地发挥学生的“再创造”能力.由此我们也可以看出，探究性学习在新课标中的地位是相当突出的，教师在数学教学中一定要给予学生足够的时间与空间以促成探究性学习的常态化.

学生在数学学习中对重点知识的理解能够做到举一反三、触类旁通离不开典型练习题的引领，离不开对这些练习题的变式发散.因此，教师在学生数学学习的过程中应突出解题方法的总结与解题规律的提炼，将一题多解、一题多变、多题一解等多种形式穿插运用于学生的数学学习中，使得学生的思维品质在分析问题与解决问题中不断提升.以下是解题多样性及变式训练的实际解题研究.

例1当x＞e时，证明ex-1＞xe-1.

引导学生探究：（1）构造函数G（x）=ex-1-xe-1能不能解决此问题呢？（2）如果不能，应该将结构如何变形或者调整呢？（3）指数式一般能转化为其他什么形式？

教师给出问题后应该引导学生进行独立的或者合作的探究，使得解题的思路与方法在探究学习中逐步形成.

首先，引导学生将指数式转化成对数式，即有当x＞e时，证明（x-1）lne＞（e-1）lnx成立.然后，构建新函数H（x）=（x-1）-（e-1）lnx进行尝试，求导后得，所以H（′x）在（e，+∞）上单调递增，故H（x）＞H（e）=0，原题得证.

另外，引导学生探究其他的证明方法并尝试对结构式进行变形.比如，两边同除以（x-1）（e-1）可得.继续构造新函数问题同样得解.

事实上，学生在数学学习的过程中不断地发现着矛盾并探究、解决着矛盾，因此，教师应充分利用数学知识发展过程中存在的问题，并引导学生进行问题的思考实现以满足学生探究的欲望.

例2若x≥0，证明

引导学生探究：（1）根据以往经验证明（fx）≥g（x）有什么方法？（2）不加变形，直接构建函数可以证明吗？（3）针对结构式，可实施哪些变形？

引导学生进行如下证明：

（1）两边同乘以ex，构建（函数值与1比较），求导的，易证G（1x）在（0，+∞）上是减函数，从而G（1x）≤G（0）=1，得证.

（3）两边同乘以e（xx+4），构造G（3x）=e（x3x-4）+x+4（数值与0比较）.设F（x）=e（x3x-4）+x+4，则F（0）=0，且F′（x）=e（x3x-1）+1，F′（0）=0.令G（x）=F′（x），则G′（x）=e（x3x+2）.因为x≥0，所以G′（x）＞0，从而函数F（x）在［0，+∞）上单调递增，即F（x）≥F（0）=0.教师在探究活动结束后让学生个体或者小组代表进行了自身解题思路的交流，使学生的解题设想与思维真正暴露在大家面前，挖掘学生思维闪光点的同时也分析了学生错误思维的原因.

引导学生探究：根据题意，用不等式的方法对此题直接证明很显然是比较难的，变形的方法其实是很多的，你有哪些想法？

引导学生诸如以下几例的尝试构造：

提出问题：①以上所有根据题意构造出的新函数对于解题能够产生实质性的帮助吗？②我们在对题目进行变形时应该将探究的重点放在哪些地方呢？

进一步引导学生进行以下式子的探究构造，检测其是否能够解决问题：

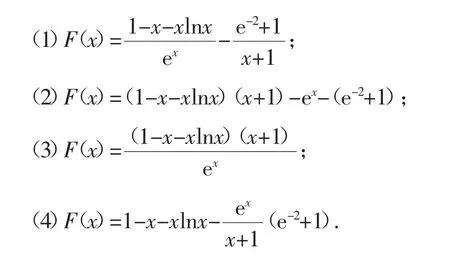
经探究发现，可行的也只有（4）式，证明如下：设h（x）=1-x-xlnx，得h′（x）=-lnx-2，所以h（x）max=h（e-2）=e-2+1.故1-x-xlnx≤e-2+1.设φ（x）=ex-（x+1），φ′（x）=ex-1，所以φ（x）在（0，+∞）上单调递增，φ（x）＞φ（0）=0，φ（x）=ex-（x+1）＞0，即.所以1）.即对任意都成立.

教师在引导学生进行此题解法的讨论结束以后可以继续引导他们进行探究过程的归纳与总结，总结可以从以下三个方面进行：①宏观角度上的解题策略的归纳，依据波利亚解题的弄清问题、拟订计划、实现计划以及回顾小结这四个步骤对问题解决的过程进行再次确认，从而使得自身对题目及题目所涉及的概念进行深层次的认识；②微观角度上的解题思路的总结；③对解题中所运用的或者隐含的数学思想方法进行归纳与总结.

习题课这一数学教学中常见的课型往往能够通过例题、习题的教学帮助学生巩固所学的概念、公式，并使学生在解题技能、掌握解题思想方法的过程中达成巩固双基、夯实基础的目的，新旧知识之间的联系，以及学生分析问题、解决问题的能力往往也能从经典的练习中得到有效的锻炼与提高，具体来说，教师在习题课的教学中可以从以下几个方面做起.

（1）用题目引动双基的复习与巩固.习题课上给学生独立完成教师精心设计的题目在很多时候并不是仅仅为了学生的习题练习，其深层的含义在于帮助学生对各知识点进行有意义的复习与巩固，这一取代知识点简单罗列的做法往往在学生的概念复习中能够取得尤为显著的效果.学生在问题解决中对概念进行了有效的复习，课堂教学内容中所涉及的基本概念、公式及方法都在解题中得到了综合的运用，双基的复习也因此有了更好的固着点与落脚点，对于概念的复习与理解也因此得到了更为有意义的提升.

（2）用典型例题的探究帮助学生释疑与纠错.教师在帮助学生复习的时候应依据学生的认知水平作出适当的延伸，为学生提供经典的例题供其进行独立的思考或是合作的探究，使得学生在讨论与探究中获得解题的思想方法，在此基础上再令学生进行探究成果的交流，使得学生解题的方法与思维一一呈现，将思维过程中科学的、不科学的东西都暴露出来，并因此得到最终的释疑纠错，最终对数学概念、公式、定理等的认识才会更加趋于成熟与完美.

（3）变式发散训练促成学生数学能力的提高.经典例题的解决并不是意味着学生探究学习活动的终止，教师还应该在此基础上进行例题变式发散的引导性训练，具体可以有以下两种做法：①教师对经典例题作出精心设计的变式问题的发散与延伸，并因此引导学生对教师所做变式进行讨论与解决；②用开放性的问题引导学生进行变式与发散的尝试，使得学生在开放性问题的引领下优化自身的思维品质.

（4）自主归纳总结促成学生认知提升.学生在例题的变式发散及延伸探究之后往往已经能够产生比较深刻的认识了，解题能力也在这一阶段得到很大的提升，教师在此时如果能够启发学生对解题方法与数学思想进行自主归纳总结的话，知识的表征往往也就在学生心中更加稳固地形成了.

数学研究与数学学习最为终极的目标自然是问题的解决，因此，对数学问题的探究便也理所当然地成为数学探究学习的主要形式.习题课中的探究学习使得以往“炒冷饭”式的复习模式遭到了颠覆，学生的自主探索、独立思考、合作交流及主动构建知识在探究性学习中得到了最为有意义的锻炼，创新意识与实践能力也在自主探究性学习活动中不断提升.