例谈高三数学二轮复习的有效选题*

☉江苏省太仓高级中学 陆 丽

例谈高三数学二轮复习的有效选题*

☉江苏省太仓高级中学 陆 丽

高三数学复习，时间紧，任务重，在有限的时间内，达到高质量的复习效果，是每一位高三数学教师追求的目标.在高三数学二轮复习中，要提高复习的效率，其核心在于选题的有效性.选题好，用好题，才能使复习有效、高效.选好题就是要选那些蕴含数学基础知识、基本技能和基本方法；蕴含多种解题思路，可以拓展学生解题视野，开阔解题思路，培养思维、思辨能力的题.怎么选题？如何选题？选题的有效立足点在哪里？笔者以高三二轮专题复习课为例，谈谈选题的策略和功能，总结选题的原则.

一、二轮复习选题须明考点、突重点

考试说明是对“考什么、怎么考、考多难”这三个问题的具体解说，因此认真研读考试说明对提高二轮复习效率起到重要的作用.研究考试说明，既要关心考点要求上的调整，又要关心弱化的考点、被删除的考点和题型示例的变化等，从而把握好高考的方向，少做无用功.在二轮复习中，教师应明确重点，对重点专题强化训练.比如，平面向量是高中数学的重要内容，高考主要从平面向量的线性运算、模、夹角、垂直与平行、基底与数量积这些知识出发，考查思维能力和创新能力.其中平面向量的数量积是8个C级考点要求之一，要求熟练掌握.而最近几年的江苏高考向量试题越来越灵活，凸显对思维能力和创新能力的考查.因此在高三二轮专题复习时有必要开设“向量问题的解题策略”的专题学习.笔者曾开设了这一节大市级公开课，从一道高考题出发，让学生领悟解决向量问题的几种策略，从而突破高考重点.

案例1（2016年江苏卷）如图1，在△ABC中，D是BC的中点，E，F是AD上的两个三等分点，则的值是_________.

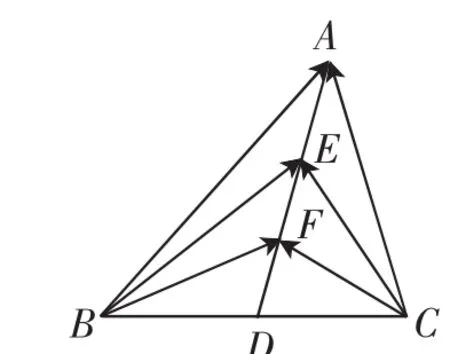
图1

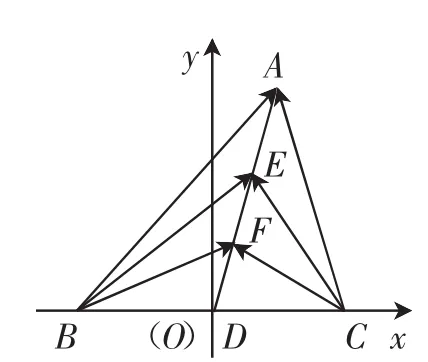
图2

视角1：坐标化.以直线BC为x轴，线段BC的中垂线为y轴，建立如图2所示的平面直角坐标系xOy，设A（3m，3n），B（-a，0），C（a，0），则，则

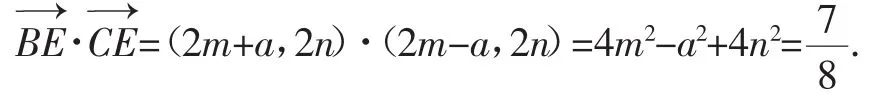
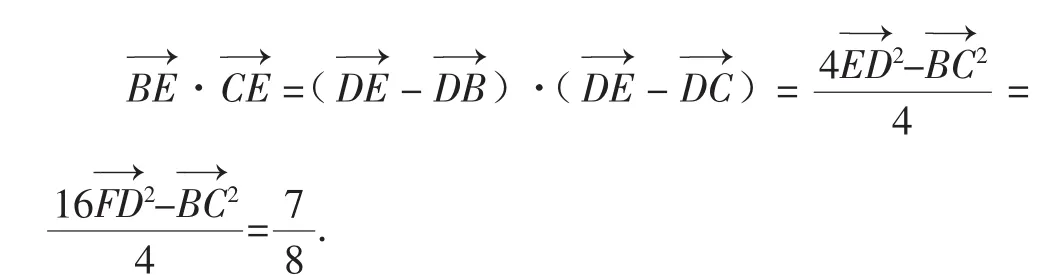
视角3：特殊化.特别地，取△ABC为等腰三角形，其中AB=AC，再坐标化求解.

课堂上学生畅所欲言，在沟通中进行思维的碰撞，学生真正弄清向量的工具性一般体现在以下两个方面：（1）利用其形的特点，通过向量运算的几何意义将其转

高中数学课堂活动组织策略研究》的阶段性研究成果（课题编化为平面几何的有关知识进行计算；（2）利用其数的特征，通过建立平面直角坐标系，将向量问题代数化来求解.这样的题目必定在二轮复习中起到高效复习的作用，提升了学生数学核心素养.

二、二轮复习选题须重方法、重迁移

高三二轮复习需要以知识复习为主线，以方法复习为暗线，两线推进，相互交织，知识中包含方法，方法中蕴含知识.因此在高三二轮复习课选题中，理应突出方法的主导地位，就法选题，使学生在掌握知识的同时，领会其中蕴含的方法，适时迁移运用，以期举一反三、以一当十、事半功倍.比如，在高三二轮专题复习“基本不等式”中，笔者以一道条件最值问题为根，通过各种变式探究此类问题的解题方法，从而提高学习效果.

案例2 若正实数a，b满足ab-4a-b=0，求ab最小值.

视角2：消元法和基本不等式求解.由ab=4a+b，得b=.因为b＞0，所以16，当且仅当4（a-1）=，即a=2，b=8时取等号.故ab的最小值为16.

在师生共同解决例题后，笔者设计了一组变式训练.

变式1（变条件）：若正实数a，b满足ab-4a-b=1，求ab最小值.

变式2（变结论）：若正实数a，b满足ab-4a-b=0，求a+b最小值.

变式3（条件结论同时变）：设x，y为实数，若4x2+y2+xy=1，求2x+y的最大值.

对于变式3来说，大部分学生都提出可直接利用基本不等式（凑目标）解决，也有少部分学生提出可利用三角消元法求解，即

通过这一组问题的研究，使学生真正厘清条件最值问题的处理方法和注意点，课堂上学生思维非常活跃，提出了很多有见解的想法和思维.这样的题目不仅能高效复习知识方法，更能激发学生探究问题的欲望，提升了学生的思维能力.

三、二轮复习选题须高视角、成系统

高考命题多在知识的交汇处命题，通过第二轮复习，进一步引导学生形成知识系统化，必须高视角研究、挖掘问题，这样才能胸有成竹，在高考中遇“新”不慌.比如，在高三二轮专题复习“应用题”中，笔者选用了一道经典题，以期能有效锻炼和提升学生的思维能力.

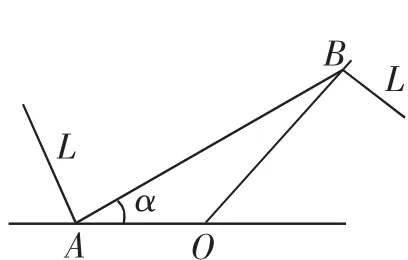
图3

案例3 如图3，某城市有一条从正西方AO通过市中心O后向东北OB，现要修一条地铁L，在OA上设一站，在OB上设一站，地铁在AB部分为直线段，现要求市中心O与AB的距离为10km，设地铁在AB部分的总长度为ykm.

（1）按下列要求建立关系式：

（i）设∠OAB=α，将y表示为α的函数；

（ii）设OA=m，OB=n，用m，n表示y.

（2）把A，B两站分别设在公路上离中心O多远处，才能使AB最短？并求出最短距离.

本题主要考查了解三角形在实际问题中的应用，综合考查了正弦、余弦定理、基本不等式、导数等知识，解题的关键是合理的把实际问题转化为数学问题.

本题的第（1）问可从“设角”和“设边”两个不同角度建立目标函数.若从“设角”的角度来看我们可从三种不同视角建立目标函数.

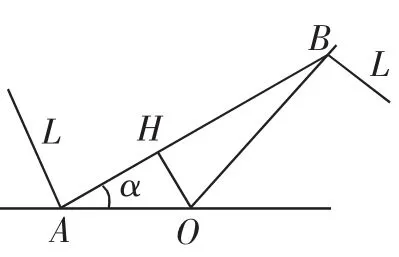
图4

视角1：转化到特殊三角形中求解.过O作OH⊥AB于H，OH=10（图4）.由题意知，∠OAH=α，∠OBH=∠AOB-

当然也可过B作BK⊥OA于K，过O作OH⊥AB于H（如图5），在△AHO中

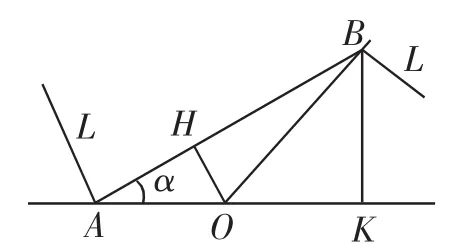
图5

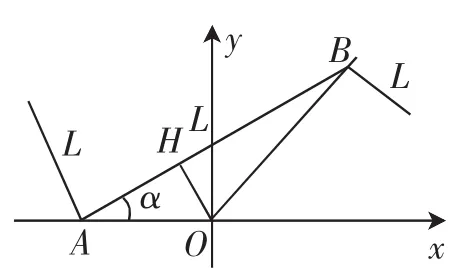
图6

在△AKB中，BK=AB·sinα=ysinα，AK=AB·cosα=ycosα.在△BKO中

视角2：运用正弦定理和等面积法求解.如图4，在△OAB中，利用正弦定理所以利用S，即可求得y.

视角3：通过建立直角坐标系，将平面几何问题转化为代数问题.以OA所在的直线为x轴，O为坐标原点，建立如图6所示的直角坐标系.过O作OH⊥AB于H，OH=10.因为，所以，即H（-10sinα，10cosα）.因此直线AB的方程为y-10cosα=tanα（x+10sinα）.令y=0，得令y=x，得即）.利用两点间的距离公式即可求得y.

从“设边”的角度来看我们也有三种不同的视角建立目标函数.

本题的第（2）问是研究目标函数的最值，我们可从四种不同视角研究此函数的最值.

或导数求y的最小值.

数学课堂的重要任务是学生吸收知识和掌握方法，但更为重要的是转化为他们自身的能力，这就需要教师在二轮复习时选好例题，以期借助例题构建自己的知识体系，从而使知识方法系统化，思维能力进一步提升.

永远没有完美的课堂，也没有完美的题目.因此高三二轮复习要有发展意识，要让学生热爱课堂，真正融入课堂，成为课堂的主人，这需要每位数学教师的不懈努力.

1.张春杰.高三数学复习课选题的四重境界［J］.上海中学数学，2014（6）.

*本文系江苏省“十三·五”规划课题《“多维互动对话”环境下号：C-c/2016/02/83）.