例谈习题课的几种教学方式

☉江苏省南通中学 周福云

例谈习题课的几种教学方式

☉江苏省南通中学 周福云

怎样解题与上好习题课是中学数学教学的一个重要环节.习题课既是教师对学生独立思考活动的指导过程，也是学生学会运用所学基础知识，加强基本技能、基本训练的必由之路，又是为实现教会学生怎样解题而采用的一种教学方法.

但在习题课教学中，教师既要选择典型例题讲解示范，又要选择习题供学生练习，然而课堂时间有限，因而确定习题课型与选择习题是上好习题课的关键.本文结合自身的教学实践，谈谈习题课的几种教学方法，求教于同行.

一、多题一类

在习题课的教学中，老师们经常会将本节课的习题分类别，例如，同样属于三角函数题型的一起讲评等.这种分类题组的方式受到大部分教师的欢迎，可以将知识点串联起来讲解.例如，三角函数应用题中，有一类问题以扇形内接变动多边形设计问题为背景，研究方向同样是研究内接多边形在扇形内变动时的面积最值问题.求解方法都是设自变量为角α，由扇形的限制得出α的取值范围，接着用三角函数表示面积，然后通过三角变换，把形如y=asinx+bcosx的函数转化为形如y=Asin（ωx+φ）的函数，从而使问题得到简化，使学生感受到以角为自变量的优点，这个过程中蕴涵了化归思想，可以将这类题一起归类讲解.

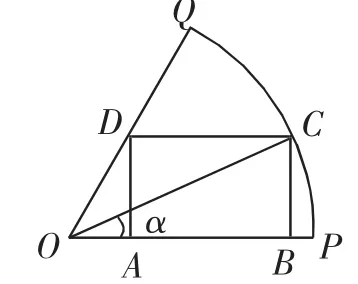
图1

（1）找出S与α之间的函数关系；

（2）由得出的函数关系，求S的最大值.

例2现有四分之一圆形的纸板（如图2），∠AOB=90°，圆半径为1，要裁剪成四边形OAPB，且满足AP//OB，∠OAB=30°，∠POA=θ，记此四边形的面积为f（θ），求f（θ）的最大值.

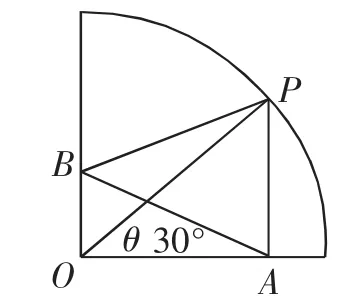
图2

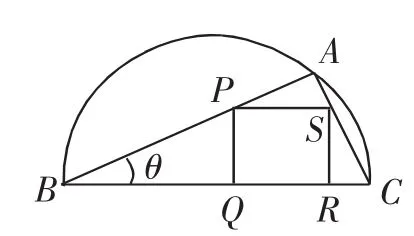
图3

例3如图3所示，在直径为BC的半圆中，A是弧BC上一点，正方形PQRS内接于△ABC，若BC=a，∠ABC=θ，设△ABC的面积为S1，正方形PQRS的面积为S2.

（1）用a，θ表示S1和S2；

二、一题多变

受多题一解的启发，我们反过来思考一题多变的问题.这里的“一题”即是“母题”，那么“母题”又是什么？母题不仅是高考题目的原型，还是具有多知识点的综合题目，只要将“母题”全面掌握，那么通过“母题”衍生的题目就更加简单.简单而言，母题就是考试过程中所有题目的“根据”；“考题”指的就是在母题中衍生的题目.千变万化的各类考题都不可能离开母题，母题是最能体现学科知识和解题技巧的题.

在进行习题课课堂教学的时候，运用“母题思想”，采用一题多变的教学方式，以一道母题进行辐射、拓展，延伸到各个知识点，能够优化方法、整合思维、融会贯通，达到解一题会一类的效果，从而使自己的知识能够充分应用到解题过程中，转化学生数学的思想方式，提高学生对数学学习的热情和积极性.

例4 利用函数的单调性证明不等式ex＞1+x（x≠0）.（人教A版选修2-2教材第32页习题B组第1大题第3小题）

分析：要想对不等进行证明，主要方式就是作商或者作差，之后通过创建函数，通过最值实现不等式的证明.根据题目可以使用作差法.

证明：设f（x）=1+x-ex，x∈（-∞，+∞），则f′（x）=1-ex，令f′（x）＞0，得x＜0，令f′（x）＜0，得x＞0.所以f（x）在（-∞，0）上单调递增，在（0，+∞）上单调递减.所以当x≠0时，（fx）＜（f0）=0，即1+x-ex＜0，所以ex＞x+1（x≠0）.

点评：虽然本题并不难，但是却非常重要，在各种考试中经常出现，其重要性可以和课本中重要的定理、定义、性质及例题相提并论.

变式1求函数f（x）=1+x-ex的单调区间，并比较与e的大小.

分析：通过其题根，并且对其进行赋值，就能够得到证实的不等式.

解析：f（x）的定义域为（-∞，+∞），f′（x）=1-ex，令f′（x）＞0，得x＜0，令f′（x）＜0，得x＞0.所以（fx）的单调递增区间为（-∞，0），单调递减区间为（0，+∞）.当x＞0时，（fx）＜（f0）=0，即1+x＜ex，令

本题主要对课本中的题根进行了考查，表现了高考题目源于课本并且高于课本，也直接使用了课本中的题根.

变式2设a＞1，函数（fx）=（1+x2）ex-a.

（1）求（fx）的单调区间；

（2）证明：（fx）在（-∞，+∞）上仅有一个零点；

（3）若曲线y=（fx）在P处的切线平行于x轴，并且在M（m，n）点的切线和直线OP相互平行（O是坐标原点），证明：

分析：（1）能够利用导数对函数单调性进行研究（.2）能够通过函数零点合理处理函数单调证明问题（.3）能够通过函数结合导数意义创建等式，根据需要正式的结论通过分析方法，在代换等式之后就能够得到只需要证明的不等式，也就是题根.

解析：（1） 由于f（′x）=2xex+（1+x2）ex=（x+1）2ex，x∈R.因为对任意x∈R，都有f（′x）≥0，所以（fx）的单调递增区间为（-∞，+∞），无单调递减区间.

（2）证明：由（1）知，（fx）在（-∞，+∞）上单调递增，且因为a＞1，所以所以故ea-1-1＞0，故所以，使得（fx0）=0.

又因为（fx）在（-∞，+∞）上单调递增，所以（fx）在（-∞，+∞）上仅有一个零点.

（3）证明：f′（x）=（x+1）2ex，令f′（x）=0，解得x=-1，所以点，所以又因为（fx）在点M（m，n）处的切线与直线OP平行，所以f（′m）=kOP，即（m+1）而要证只需证

令h′（x）＞0，解得x＞0，令h（′x）＜0，解得x＜0.所以h（x）在（-∞，0）上单调递减，在（0，+∞）单调递增，所以h（x）≥h（0）=0，所以ex≥x+1，所以m+1≤em，所以1，结论得证.

本题将课本题根作为基础试题的创建，对函数研究过程中导数的使用和分析进行了考查.第（3）问比较隐秘，如果使用分析方法实现逆向思考就会使题目变得简单.

变式3设函数（fx）=ex-ax-1.

（1）若函数（fx）在R上单调递增，求a的取值范围；

（2）当a＞0时，设函数（fx）的最小值为g（a），求证：g（a）≤0；

（3）求证：对任意的正整数n，都有1n+1+2n+1+3n+1+…+nn+1＜（n+1）n+1.

分析：（1）通过等价转化使其成为恒成立问题（.2）通过导数对函数最值进行全面的研究（.3）通过题目能够得到课本中的题根，并且对其进行赋值，将其转化为等比数列的求和.

解析：（1） 通过题意知，f′（x）=ex-a≥0对x∈R恒成立，且ex＞0，故a的取值范围为a≤0.

（2）证明：由a＞0，及f（′x）=ex-a可得，函数（fx）在（-∞，lna）上单调递减，在（lna，+∞）上单调递增，故函数（fx）的最小值为g（a）=f（lna）=elna-alna-1=a-alna-1，则g′（a）=-lna，故当a∈（0，1）时，g（′a）＞0，当a∈（1，+∞）时，g（′a）＜0，从而可知g（a）在（0，1）上单调递增，在（1，+∞）上单调递减，且g（1）=0，故g（a）≤0.

（3）证明：由（2）可知，当a=1时，总有（fx）=ex-x-1≥0，当且仅当x=0时等号成立.故当x＞0时，总有ex＞x+1.于是可得（x+1）n+1＜（e）xn+1=e（n+1）x.

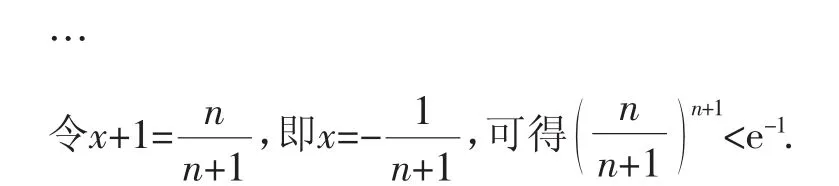
故对任意的正整数n，都有1n+1+2n+1+3n+1+…+nn+1＜（n+1）n+1.

点评：此题作为使用课本中题根效果最好的题目，结合数列知识，将知识交汇处的命题思路充分地体现了出现，并且得到了数列不等式.

三、一题多解

在进行习题课教学的时候，同一个数学问题，经常可以使用不同的方法和途径来解决，即“母题思想”中的一题多解，这种习题课教学方式有利于透析各类概念的内涵和外延，加深学生的理解，培养学生的发散性和创造性思维.多种解法分析比较，寻找解题的最佳途径和方法能更好地巩固知识，提高学生的解题能力.

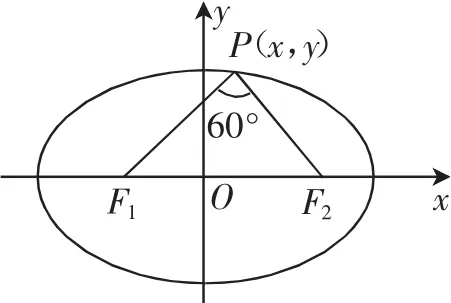
图4

解法1：如图4，令P（x，y），

由椭圆的定义知，|PF1|+|PF2|=2a=10，

在△PF1F2中，由余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1·||PF2|cos60°.

因此△PF1F2面积为

图5

解法2：如图5，令|PF1|=m，|PF2|=n.

∴|F1F2|=2c=5.由椭圆的定义知，|PF1|+|PF2|=2a=10.

即m+n=10.

两边平方得m2+n2+2mn=100.①

在△PF1F2中，由余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1·||PF2|cos60°，

故m2+n2-mn=25.②

①-②，得3mn=75.∴mn=25.

因此△PF1F2面积为

解法3：令∠PF1F2=α，由解法2可知，m+n=10，|F1F2|=5.在△PF1F2中，由正弦定理知，

解得sin（α+30°）=1.又0°＜α＜120°，故α=60°.这样△PF1F2为等边三角形.

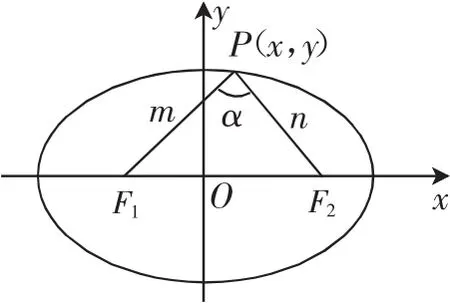
图6

解法4：如图6，令|PF1|=m，|PF2|=n，由椭圆的定义知，m+n=2a.两边平方得

m2+n2+2mn=4a2.①

在△PF1F2中，由余弦定理知，

|F1F2|2=|PF1|2+|PF2|2-2|PF1·||PF2|cosα.

故m2+n2-2mncosα=4c2.②

因此△PF1F2面积为

叶澜教授曾经提到过：“课堂作为通向未知方向的途径，在此过程中会发现意外通道及美丽，并不是都要通过循序固定路线，而缺少激情.”在进行教学过程中，要为学生留一些自由思考的空间和实践，教师不能够知是根据自己设置的思路进行教学，这样会对学生的思维造成限制，使学生的思维强制扭转，在刚出现题目的时候就对学生进行提示和分析，这样只会将学生自主思维能力扼杀在摇篮中，对学生自由创造空间进行剥夺，在学生还无法思考的时候，教师使用自己的思路对学生的大脑进行限制，使学生服从自己的模式，严重阻碍了学生思维能力的培养.

在中学数学习题课教学中，若能引导学生充分观察习题特征，挖掘解题规律，研究各类题型，将其归为多题一解或一题多解的类型去分析，就可以掌握命题根本，拓宽解题思路，多方位、多角度地把知识进行联系，搭建知识框架，厘清知识脉络，从而帮助学生极大地提高解题的效率及准确率.这样一来，习题课教学的有效性才能得到凸显.