例谈直线与圆中的最值问题

☉江苏省江阴市第二中学 张志刚

例谈直线与圆中的最值问题

☉江苏省江阴市第二中学 张志刚

直线与圆的位置关系是高中数学一个非常重要的内容，它涉及的知识点较多，题型也千变万化.最值是数学知识体系中的重要内容，也是数学中最具挑战性的问题.高考命题者对直线与圆知识中的最值问题常常是情有独钟，这种导向性使得该知识成为教学中的重点与难点.从问题解决的思路来看，学生要想顺利地解决此类问题，需要综合运用几何与代数的相关知识与方法，以及数形结合等思想，并在此过程中寻找到解决最值问题的方法.本文通过教学实践，枚举几例直线与圆中的最值问题，以供参考.

一、直线与圆相交构成的三角形面积最值

最值问题中有一类基本题型，就是一条直线与圆相交时所形成的两个交点与圆心可以构成一个三角形，由于直线的动态性，所以该三角形的面积就存在一个最值.在教学中发现，学生在遇到此类问题时思维常常是混乱的.来看一个例子：

例1 平面直角坐标系中有点P（-3，4），圆C：（x+1）2+y2=4.过点P作直线l与圆相交于A，B两点，求△ABC面积的最大值.

解法1：显然直线l的斜率存在且不为零.设直线l的斜率为k，方程为kx-y+3k+4=0.

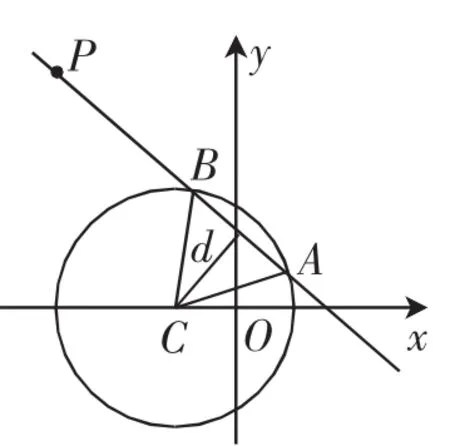
图1

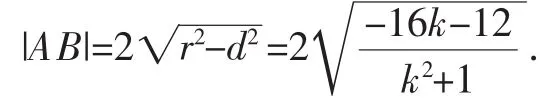
接下来求出此函数的最大值（此略）.

解法2：显然直线l的斜率存在且不为零.设直线l的斜率为k，方程为y=k（x+3）+4.圆心C（-1，0）到直线l的距离

设A（x1，y1），B（x2，y2），则

接来下求出此函数的最大值（.以下略）

解法3：如图1所示，当且仅当∠ACB=90°时取等号.

故△ABC面积的最大值为2.

比较三种方法，显然第三种简洁方便.

二、由切线构成的四边形面积最值

例2 已知P是直线l：3x-4y+11=0上动点，PA，PB是圆x2+y2-2x-2y+1=0的两条切线，A，B为切点，C是圆心，那么四边形PACB面积的最小值为_______.

解：圆的标准方程（x-1）2+（y-1）2=1，圆心（1，1），r=1，如图2.

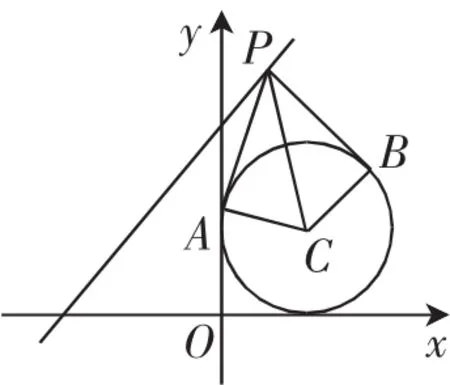
图2

故当|PC|最小值，SPACB最小.

分析：在计算中我们选择已知的信息量大的，便于计算.

解法1：

当∠AOB=90°时，三角形面积最大.

这就转化成了我们所熟悉的问题.

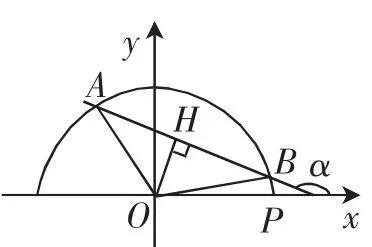
图3

解法2：设直线l的倾斜角为α，

转化与化归思想是重要的数学思想.本题中将所求问题转化成计算圆的弦长、弦心距，再利用点到直线的距离使问题迎刃而解，更好地提高学生的解题能力.

三、根据线性规划思想求的最值问题

根据所求代数式结构，考查它的几何意义，数形结合思想，以及线性规划思想的体现.

例4 已知P（x，y）是圆（x+2）2+y2=1上任一点.

（2）求3x+4y的最值.

解：（1）如图4，设A（1，2），则直线PA的斜率即kx-y-k+2=0.

问题转化为直线与圆有公共点（相交或相切）时k的范围，利用直线和圆的位置关系求解.

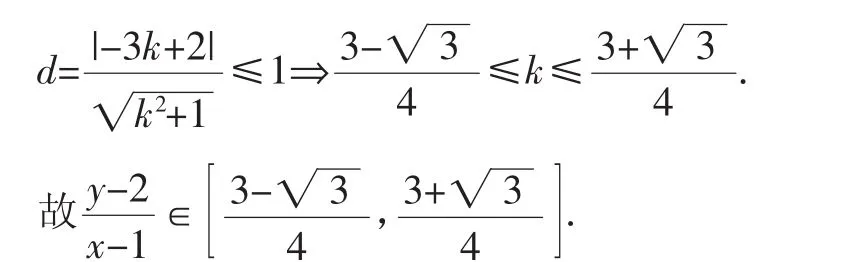
图4

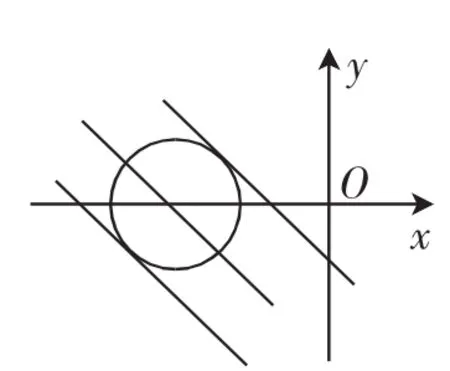
图5

（2） 如 图 5， 令 z=3x+4y， 即 3x+4y-z=0

问题转化为直线与圆有公共点（相交或相切）时z的范围，利用直线和圆的位置关系求解.

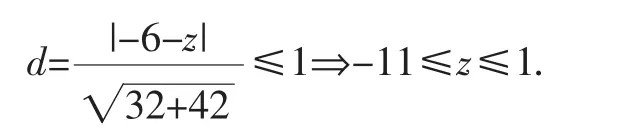
故3x+4y∈［-11，1］

例5 x，y满足x+2y-5=0，求（x+1）2+（y+1）2的最小值.

解法1：设，d表示P（x，y）与Q（-1，-1）连线的距离.

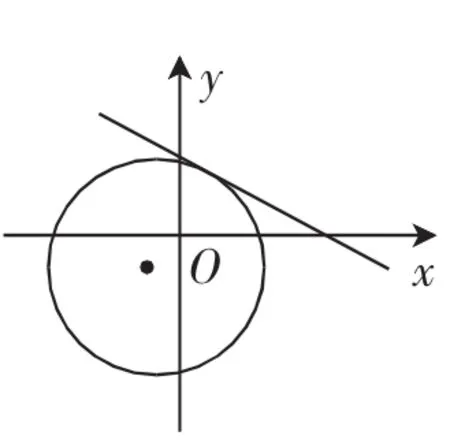
图6

解法2：令（x+1）2+（y+1）2=r2表示以Q（-1，-1）为圆心，r为半径的圆，r2最小，即r最小，此时直线与圆相切

当然除了上述与几何图形结合，利用几何性质及位置关系，求取最值方法外，还有一些代数方法，如函数法、重要不等式法等.

如例5中，x+2y-5=0，则x=5-2y，（x+1）2+（y+1）2=（6-2y）2+（y+1）2=5y2-22y+37

代换消元整理成一元二次函数，利用二次函数解决最值.

总之，应给学生思考空间，引导其思考，帮助其分析，指导其归纳总结，并在平时加强训练，强化运用.

在直线与圆中，常考的最值问题有：圆外一定点与圆上一动点间的距离；直线与圆相离，圆上点到直线的距离；直线与圆相离，过直线上一点作圆的切线，切线长的计算；过圆内一点的弦长的范围；两圆相离，两圆上动点间的距离.需要学生准确理解已知量、待求量的几何意义，准确转化为直线与圆的位置关系，涉及切线长的最值时，注意切线长、半径、圆心与切线另一端点连线能构成直角三角形，涉及弦长时，半径、弦心距、弦长一半，构成直角三角形；与圆有关问题，数形结合，特别关注圆的圆心、半径，这两个基本几何属性与其他点、线产生联系.

四、结束语

高中数学解题能力的培养关键在于抓住问题的本质.数学解题讲究入乎其内、出乎其外，学生需要从丰富的题境中寻找有效条件，体会题目的内涵与命题者所要考查的意图.日常的习题教学中，教师要超越试题本身，要从方法的角度培养学生的解题能力，这样学生才能清楚地看到题目的本质，从而对一类题型形成规律性认识.

同时，高中数学解题中，教师还需要重点进行基于学生可能思路的解题设计，学生在解题的过程中要获得的不仅是解题能力，还要落实核心素养.尤其是学生与学生之间的交流，常常是学生解题思路得以提升的重要阶梯，教师要善于通过学生的发言，总结出一些学生认知中的规律性认识，进而上升为清晰的解题思路，这样学生在学习中往往可以更有成就感.