例谈转化与化归在解题中的运用

☉南京师范大学第二附属高级中学 朱 斌

例谈转化与化归在解题中的运用

☉南京师范大学第二附属高级中学 朱 斌

等价转化的思想方法是数学思想方法中的重要思想方法，但很多学生在解题过程中，缺乏等价转化思想的应用，有时根本想不到用等价转化的思想方法解题，因此，笔者结合自身的教学实践，剖析如何在教学中灵活运用等价转化思想解题，从而促进解题能力的提高.

一、领会题中条件意义是转化与化归的重要前提

一般来说，题目中所给条件含有丰富的内容，因此要引导学生认真读题，仔细审题，依据所给的条件步步为营，稳扎稳打，不断朝着目标转化.

例1

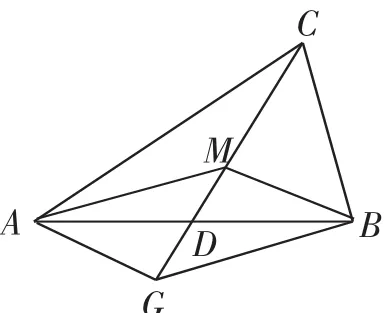
图1

对于这道题，学生入手很困难，如何正确认识题中条件，如何转化条件是最大的障碍.可以引导学生从重心入手：如图1所示，点M为△ABC的重心，则结合已知条件解出，代入已知等式，得，即但与为不共线的非零向量，所以即

二、数形结合是转化与化归中的重要方法

在方程与函数这类问题中，常常涉及方程解的问题、恒成立问题或函数交点等问题.若能根据题意，利用数形结合的思想，灵活转化方程或函数，便可迅速、快捷地解决问题.

例2已知函数与a）图像上存在关于y轴对称的点，则a的取值范围是________.

转化1：由题意知，存在x0∈（-∞，0）满足f（x0）=g（-x0），得

当a≤0时，当x趋近于a时，那a-x趋近于0时，h（x）=趋近于+∞，所以符合题意.

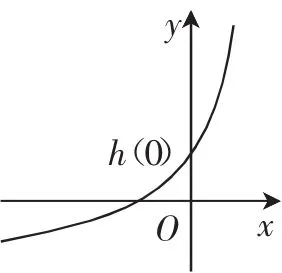
图2

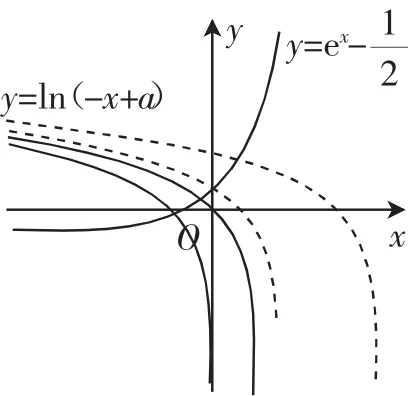
图3

转化2：由题意知，存在x0∈（-∞，0）满足得那么，如图3所示，分别作出的图像，利用图像数形结合可得得

数形结合是数学学习的一个重要特点，常常利用图像来提供解题思路，根据数据的计算来精确问题的结果.

三、建立目标意识是转化与化归的主流思想

在高中数解题中，若从题目的条件中找不到突破口，那么，建立目标意识就是首要的解题思想.例如，针对近几年的多变量问题，不少学生在面对此类问题时，感到无从入手，难以找到切入点.

例3已知常数a＞0，函数

（1）讨论（fx）在区间（0，+∞）上的单调性；

（2）若（fx）存在两个极值点x1，x2，且（fx1）+（fx2）＞0，求a的取值范围.

解：此处仅对（2）进行分析：

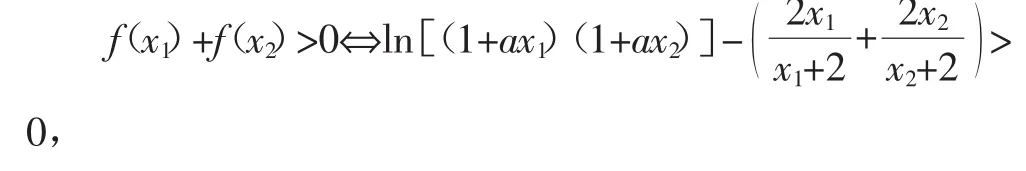
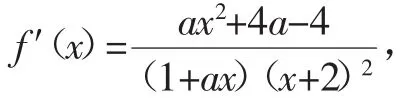
因为x1，x2是f（′x）的零点，所以有

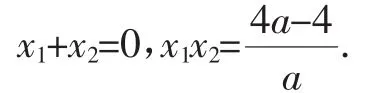
通过转化将双变量问题转化为单一变量问题，题目自可迎刃而解.

四、换元思想有助于转化与化归的使用

有的题目常常通过换元，将题目转化成比较容易解决的问题.

（1）求椭圆C的方程.

（ii）求△ABQ面积的最大值.

设P（2cosα，sinα），

则Q（4cos（α+π），2sin（α+π）），即Q（-4cosα，-2sinα），

（ii）设A（4cosθ，2sinθ），B（4cosφ，2sinφ），由椭圆的对称性及直线AB与椭圆C有公共点，知线段AB的中点M（2cosθ+2cosφ，sinθ+sinφ），在椭圆C上或其内部，则，，整理得，从而

本题通过三角换元，将问题转化为三角函数中的问题，大大简化了求解过程，达到了事半功倍的效果.

例5已知椭圆的一个焦点为，离心率为

（1）求椭圆C的标准方程；

（2）若动点P（x0，y0）为椭圆外一点，且点P到椭圆C的两条切线相互垂直，求点P的轨迹方程.

（2）当切线的斜率存在且不为0时，设过P（x0，y0）点的切线为y-y0=k（x-x0），令则x=3X，y=2Y，于是椭圆转化为圆X2+Y2=1，切线y-y0=k（x-x0）转化为3kX-2Y-kx0+y0=0，由于伸缩变换后圆与直线仍是相切的，故圆心到直线的距离即

本题通过代数换元将椭圆问题转化为圆的问题来解决，减少了运算量，降低了思维的难度，提高解题的正确率.

“解题就是把要解的题转化为已经解过的题”.因此，任何数学问题的解决归根结底都是将不熟悉的问题转化为熟悉的问题，将繁难的问题转化分解为简单易行的问题.因此，在平时的教学中，我们应该不断培养和训练学生观察知识间的纵横关系，增加转化的意识，注重等价转化思想的渗透，不断提高解题能力，提升数学素养.