基于改进m序列的压缩采样观测矩阵设计

崔兴梅， 吴 键, 徐云鹏

(南京理工大学机械工程学院 南京，210094)

基于改进m序列的压缩采样观测矩阵设计

崔兴梅， 吴 键, 徐云鹏

(南京理工大学机械工程学院 南京，210094)

为了降低对嵌入式系统数据采集的硬件要求，提出了一种适用于模拟信号采集系统的压缩采样方法，为压缩感知观测矩阵提供了一种低功耗硬件实现方法。介绍了观测矩阵设计的相关要求，并提出了带压缩采样矩阵的高斯随机观测矩阵及基于改进的m序列的压缩采样矩阵硬件实现方法。考虑系统功耗及外围电路复杂度问题，提出利用MSP430微处理器完成压缩采样系统设计，并利用滚珠丝杠动态测试中的振动信号完成对系统的验证。实验结果表明，该系统能以低于亚乃奎斯特采样频率的采样率对振动信号进行压缩采样，能较为精确地重构出原始信号。

观测矩阵；改进型m序列；滚珠丝杠振动信号；MSP430G2微处理器；压缩采样

引 言

在许多嵌入式信号处理系统中，如何使用稀缺的物理资源来获得满意的性能是一个根本性的挑战。例如，分布式现场传感器需要有效地进行自主的数据采集和无线传输，但是在这个过程中会受到许多物理条件的限制，如覆盖范围、检测灵敏度及系统的鲁棒性等，这就需要对实际应用中的硬件系统降低要求。解决该问题的一个有效方法是减少采集和处理一些不必要的或者多余的数据。传统的传感技术采集的数据总量远远超过所需的数据量，在大多数情况下，往往只有小部分数据是实际有用的，其余的都不会对处理结果造成影响，可以被丢弃。因此，文献[1-2]提出了压缩感知(compressed sensing, 简称CS)理论。

压缩感知的基础理论研究主要包括稀疏变换基的选择、观测矩阵的设计与实现及信号重构算法研究等[1]。其中，压缩感知的观测过程是对稀疏信号的线性非自适应性测量，这是一个高维稀疏向量降维的过程，也是一个计算完备的信号稀疏系数向量的过程。如今，压缩感知理论没有在更广阔领域得到应用，主要原因就在于压缩感知的观测过程难以在硬件电路中得到实现，从而难以应用于实际工程之中。

在将压缩感知理论应用于模拟信号采集的研究中，文献[3-4]提出了一种应用模拟信息转换器( analog-to-information conversion, 简称AIC)实现压缩采样的方法，该转换器使用积分器或低通滤波器完成对信号的调制，即压缩采样，在后续处理中实现对数据的重构。文献[5-6]针对模拟信息转换器做出了研究，提出了改进的模拟信息转换器硬件实现方案。由于模拟信息转换器在对信号调制(压缩采样)时，所需积分支路由所需信息采样点数决定，因此需要大量的积分器或低通滤波器电路，在硬件上难以实现。

笔者首先介绍了观测矩阵需要满足的有限等距约束(restricted isometry property, 简称RIP)准则，设计了用于硬件微处理器实现的观测矩阵方案，并对其观测性能参数做出了分析与计算；其次，设计了利用改进的m序列产生随机采样序列的方法，并利用数字电路和微处理器实现对一般的连续模拟信号的压缩采样；最后，利用滚珠丝杠动态测试中的振动信号完成对系统的实验验证。

1 观测矩阵设计及性能仿真验证

设计观测矩阵时，一般需要满足RIP准则和不相干性准则等[7]。同时，由于本研究主要针对待测振动信号进行压缩采样，还需要满足时间性要求。

1.1 矩阵的不相干性

矩阵的不相干性是指在相干测量中两个不同矩阵中任意行列间的最大相关性[8]。现假设存在一个n×n的矩阵ψ，其中，ψ1,ψ2,…,ψn表示其每一个列向量。存在一个m×n的矩阵Φ，其中，Φ1,Φ2,……,Φm作为其行向量，则相干系数μ被定为

(1)

其中：1≤j≤n；1≤k≤m。

在压缩采样中，稀疏矩阵和观测矩阵的相干性可以反映观测矩阵的性能。它们的相干系数越大，系统需要观测的点数就越多。

1.2 矩阵的RIP准则

对于观测矩阵ψ，文献[1-2]在压缩感知理论的基础上给出并证明了其必须满足的PIP准则。RIP准则从数学角度给出了某一矩阵作为观测矩阵需要满足的不等式条件。

对于任意c∈R|T|和常数ξK∈(0,1)，如果

(2)

成立，其中T⊂{1,2,…,n},|T|≤2K。ψT为K×|T|的子矩阵，由ψ中选出的相关的列构成，则矩阵ψ满足RIP[9]准则。

1.3 压缩采样的时间性要求

笔者主要针对待测振动信号进行压缩采样，信号是未知的，即在这一时刻不可能估计到下一时刻信号的状态。因此，对于模拟信号采集系统，观测矩阵的行向量对应信号的时间轴，所以要求上一行的最后一个非零元素要在下一行的第1个非零元素之前。例如，假设有2个4×4的矩阵作为观测矩阵

(3)

用ψ2矩阵，这个采样过程是无法完成的，因为在t1时刻进行采样时，第1行第4列的元素1对应的是信号t4时刻的状态，而在t1时刻，该状态是未知的，即

(4)

因此，ψ2类型的观测矩阵无法应用在模拟信号的压缩采样中。

1.4 压缩采样观测矩阵设计及验证

由于大多数信号具有稀疏性或在某一变换基下具有稀疏性，考虑设计观测矩阵ψSample的形式为

(5)

该矩阵被称为随机压缩采样矩阵，其构成方式为n×n的单位阵中对角线上的元素随机选出m个位置设为1，其余位置元素均为零，即对角线上元素为一随机序列。

由于该矩阵结构过于简单，不符合作为观测矩阵的RIP准则和不相干性，因此在该矩阵的基础上，对其进行改进，设计出一种用于硬件压缩采样的观测矩阵y=ψGaussianψSample。其中，ψGaussian为高斯随机矩阵，称之为带压缩采样的高斯观测矩阵。于是，压缩感知观测过程变为y=ψGaussianψSamplex。其中，由硬件实现压缩采样矩阵ψSample，对模拟信号采集少量观测点，将其余序列点补“0”，完成“一次观测”。将采集到的“稀疏序列”发送至上位机，在Matalb中采用高斯随机矩阵ψGaussian对其完成“二次观测”，二次观测完成后的向量作为压缩感知观测向量进行重构。

针对所设计的观测矩阵，选取最常用的离散傅里叶变换基(discrete Fourier transformation,简称 DFT)对其不相干性进行计算，这是因为大多数信号在该变换基下具有稀疏性。设测试信号为有512点的序列，观测次数为80，即m=80，n=512，通过1 000次独立实验，得到该观测矩阵与离散傅里叶变换基相干性参数的分布统计直方图，如图1所示。

图1 相干性参数分布Fig.1 Coherence parameter distribution

压缩感知中传感矩阵应满足有限等距约束性(RIP)的条件，K阶RIP条件要求参数ξK∈(0,1)。有限等距常数(RIC)是与有限等距约束紧密结合在一起的一个参数，具体是指满足有限等距约束性的最小ξK，该常数可以根据传感矩阵的特征值λ计算。

同样令m=80，n=512,选取离散傅里叶变换基为稀疏矩阵，根据上述原理计算，其等距约束常数为0.712 0，基本满足ξK∈(0,1)的要求。

2 基于改进m序列的压缩采样矩阵的实现

2.1 m序列的产生及性质

m序列又称伪随机序列，它的特点是不能预先确定但是可以重复产生, m序列具有平衡特性、游程特性和移位相加特性[10]。在其平衡特性中，在一个m序列的每个周期中，“1”码元出现的次数总比“0”码元多一个，两种码元数量基本相当。但是，在笔者所设计的模拟信号采集系统中采样点数要远远小于信号长度，因此，m序列并不适合做压缩采样的随机序列。鉴于此，一种改进的m序列被设计用作压缩采样的随机序列。

为了使压缩采样中的测量点数远小于信号长度，改进的m序列中，“0”出现的次数应远大于“1”的数量。因此，应在m序列发生器电路中增加一个双稳态电路和一个与门，m序列发生器的输出与双稳态电路输出做“与”运算后将结果输出到微处理器引脚，其中，m序列发生器生成的序列触发双稳态电路状态的翻转。逻辑转换过程由表1给出。

由表1可以看出，经过处理的m序列中“1”的个数减少为1/4，基本满足压缩采样点数的要求，可以用作随机采样序列。

表1 改进的m序列发生器逻辑转换表

2.2 改进的m随机序列的电路实现

通常m序列发生器由N级反馈移位寄存器构成[10]。本研究中设计了8级m序列发生器，配合双稳态电路与“与”门，输出随机采样序列。移位寄存器芯片选择双向4位移位寄存器74LS194。双稳态电路由4013双D触发器芯片构成。电路如图2所示。

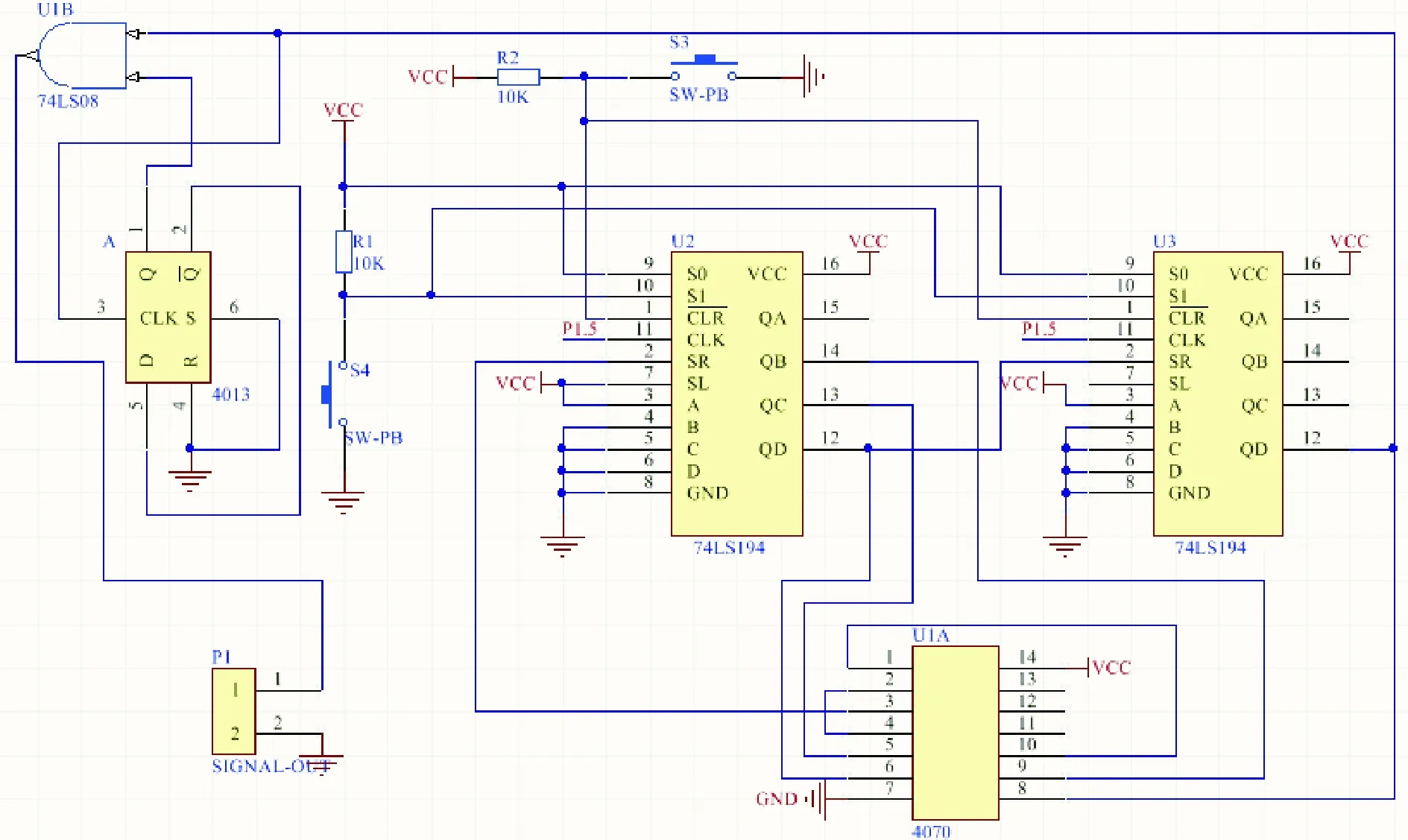
图2 改进的m序列发生器Fig.2 The improved m sequence generator

3 压缩采样系统的硬软件设计

3.1 设计需求分析及微处理器选型

一般地，模拟信号采样系统需要完成信号的AD转换、传输及处理[11-13]。笔者所设计的压缩采样系统主要是为了解决嵌入式系统中物理资源缺乏、功耗受限的问题，为了减小系统功耗，降低对硬件系统物理资源的要求，应当尽量减少系统外围电路的规模。因此，微处理器上应集成以下模块，包括片上AD/DA转换(用于信号采集)、定时器模块(用于计数)以及UART模块(用于采样完成后传输数据到Matlab)。同时，微处理器本身也应具备低功耗特性。

笔者最终选取MSP430G2型微处理器，因为该处理器具有内置的10位AD转换器、2个内部定时器模块和UART模块，基本符合系统设计的要求，可以实现低功耗、低成本的“单片”解决方案。与ARM和FPGA相比，该型微处理器具有多达5种低功耗模式，可以在超低功耗下运行。因此，笔者基于MSP430G2553型微处理器进行压缩采样系统设计，编译工具使用CCS，编程语言采用C语言。

3.2 压缩采样系统软件设计

压缩采样系统软件开发流程如下。

1) 微处理器初始化，包括关看门狗，配置时钟信号为SMCLK(辅助主时钟)。

2) 设置定时器定时时间，该时间为改进的m序列码元产生的时间间隔。此时定时器开始计时，系统进入低功耗模式LPM1，等待唤醒。

3) 定时时间到，微处理器唤醒，重装定时器初值，同时检测改进的m序列输入引脚状态。将检测结果通过UART发送至上位机，若状态为“1”，启动ADC10模块进行一次采样，将数据通过UART模块发送到上位机；若状态为“0”，则发送数据0到上位机。

具体流程图如图3所示。

图3 系统软件流程图Fig.3 The flow chart of system software

4 压缩采样系统实验验证

笔者采用滚珠丝杠动态测试中的振动信号对系统的可行性进行验证[14]，实验装置如图4所示。其中，实验信号为200～600Hz的振动信号，由激振器产生。使用加速度传感器完成数据采集，从而对滚珠丝杠的模态等相关参数进行计算[15-16]。

图4 滚珠丝杠动态测试系统Fig.4 The ball screw dynamic testing system

图5 模拟信号采集系统工作流程Fig.5 The working process of imulation signal acquisition system

本实验将利用所设计系统完成对滚珠丝杠振动信号的压缩采样，选取子空间追踪算法(SP)完成对信号的重构。图5为模拟信号采集系统的压缩采样过程及后续上位机重构流程。

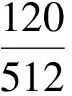
其对比实验结果如图6、图7所示。

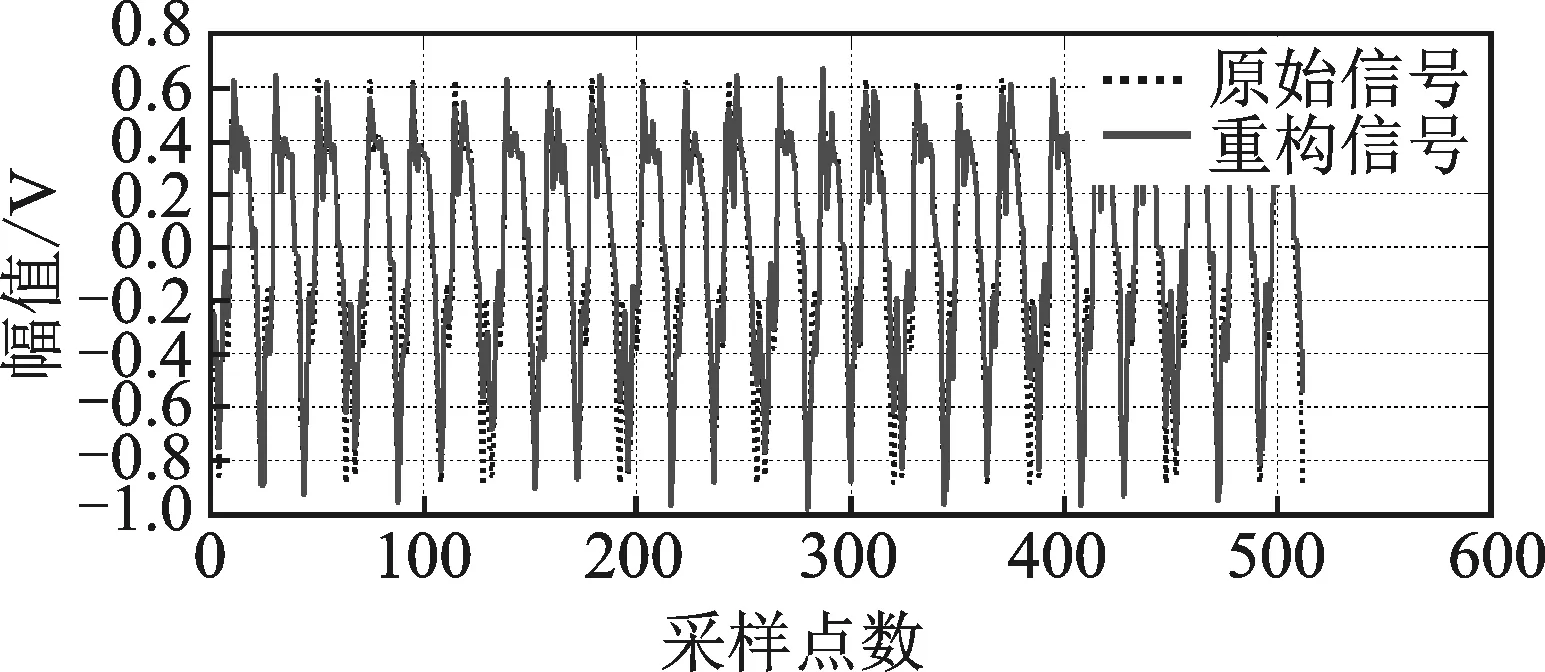
图6 压缩采样系统重构振动信号Fig.6 The reconstruction vibration signal of compressed sampling system

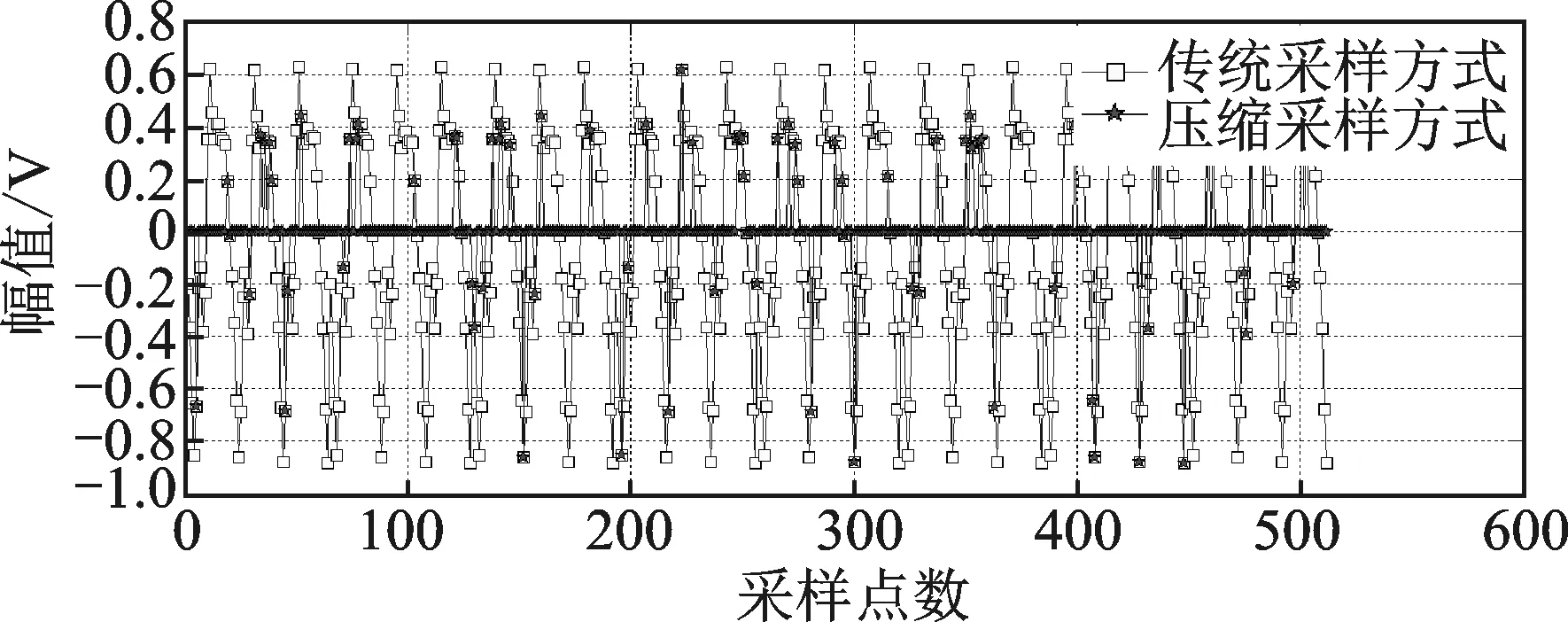
图7 传统采样与压缩采样点数对比Fig.7 The points comparison of traditional sampling and compression sampling

压缩采样过程中信号稀疏度未知，如果信号稀疏度估计存在较大误差，SP算法重构精度会受到很大的影响。在稀疏度为10的情况下残余误差不一定是最小的。因此，对于观测的120个采样点，在稀疏度从0到50的情况下，在各种稀疏度下均重构1 000次，得到2组实验信号的重构残余误差和重构时间与稀疏度的关系，如图8所示。

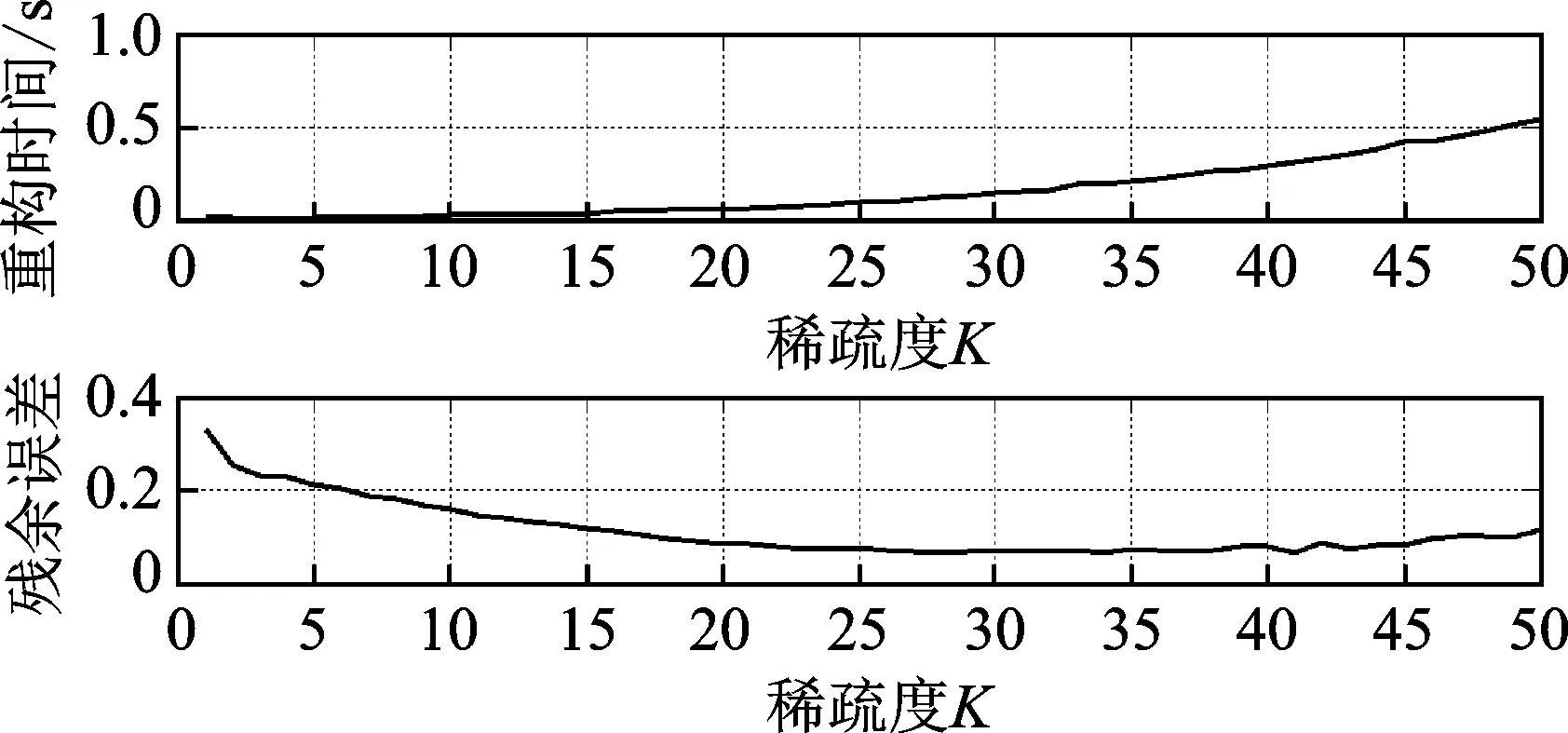
图8 不同稀疏度下信号的重构时间与残余误差Fig.8 The reconstruction time and residual error of signal on different sparsity

通过计算，在最适应稀疏度下与传统采样方法相比，基于改进m序列的压缩采样系统重构残余误差为0.0560，可以较为精确地完成原始信号的重构。

5 结束语

提出了一种基于压缩感知理论的模拟信号采集方法，为压缩感知观测矩阵提供了一种低功耗硬件实现方法，实现了硬件压缩采样过程。该方法突破了压缩感知理论仿真研究的局限性，降低了对硬件数据采集系统的要求，具有一定的实用价值。为验证系统的实用性，利用滚珠丝杠动态测试中的振动信号完成了对系统的验证。实验结果表明，该系统能够以低于乃奎斯特频率的采样率实现对相关信号的压缩采样，并根据采样数据较精确的恢复出原始信号。

[1] Donoho D L. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[2] Candes E J, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information [J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[3] Kirolos S, Laska J, Wakin M, et al. Analog-to-information conversion via random demodulation[C]∥IEEE Dallas/CAS Workshop on Design, Applications, Integration and Software. Richardson TX:[s.n.], 2006: 71-74.

[4] Laska J N, Kirolos S, Duarte M F, et al. Theory and implementation of an analog-to-information converter using random demodulation[C]∥IEEE International Symposium on Circuits and Systems. New Orleans, LA:[s.n.], 2007: 1959-1962.

[5] 陈宇科. 压缩采样中的模拟信息转换技术研究[D]. 杭州：杭州电子科技大学,2011.

[6] 刘立明. 模拟信息转换器的实现技术研究[D]. 杭州：杭州电子科技大学, 2012.

[7] Candes E J, Tao T. Near-optimal signal recovery from random projections: universal encoding strategies [J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425.

[8] Qaisar S, Bilal R M, Iqbal W, et al. Compressive sensing: from theory to applications, a survey [J]. Journal of Communications and Networks, 2013, 15(5): 443-456.

[9] 路畅, 刘玉红. 压缩感知理论中的RIP准则[J]. 自动化与仪器仪表, 2015(8): 211-213.

Lu Chang, Liu Yuhong. RIP criterion in compressed sensing theory [J]. Automation and Instrumentation, 2015(8):211-213. (in Chinese)

[10] 党骙, 马林华, 田雨, 等. m序列压缩感知测量矩阵构造[J].西安电子科技大学学报：自然科学版, 2015,42(2):186-192.

Dang Kui, Ma Linhua, Tian Yu, et al. Construction of the compressive sensing measurement matrix based on m sequence [J]. Journal of Xian University:Natural Science Edition, 2015,42(2):186-192. (in Chinese)

[11] 尚盈, 袁慎芳, 吴键, 等. 基于无线传感网络的大型结构健康监测系统[J]. 数据采集与处理, 2009, 24(2):254-258.

Shang Ying, Yuan Shenfang, Wu Jian, et al. Large-scale structural health monitoring system based on wireless sensor networks [J]. Journal of Data Acquisition & Processing, 2009, 24(2):254-258. (in Chinese)

[12] Yuan Shenfang, Mei Hanfei, Qiu Lei, et al. On a digital wireless impact-monitoring network for large-scale composite structures [J]. Smart Materials and Structures, 2014, 23(8):1-16.

[13] 杨世锡, 梁文军, 于保华. 振动信号多通道同步整周期数据采集卡设计[J]. 振动、测试与诊断, 2013, 33(1):23-28.

Yang Shixi, Liang Wenjun, Yu Baohua. Vibration signal multi-channel synchronous whole-cycle data acquisition card design [J].Journal of Vibration, Measurement & Diagnosis, 2013, 33(1):23-28. (in Chinese)

[14] 李学军, 侯彦涛, 何宽芳, 等. 集成式多功能振动信号测试系统的研制[J]. 振动、测试与诊断, 2008, 28(2):143-146.

Li Xuejun, Hou Yntao, He Kuanfang, et al. The development of the integrated multi-functional vibration signal test system [J]. Journal of Vibration, Measurement & Diagnosis, 2008, 28(2):143-146. (in Chinese)

[15] 何博侠, 董香龙, 程寓, 等. 滚珠丝杠动态特性参数的测试装置: 中国，CN203178071U[P].2013-09-04.

[16] 翁健光, 袁军堂, 汪振华，等. 滚珠丝杠副静力学特性分析[J]. 制造技术与机床, 2012(11):127-130.

Weng Jianguang, Yuan Juntang, Wang Zhenhua, et al. Analysis on statics characteristic of ball screw[J]. Manufacturing Technology and Machine Tools, 2012(11):127-130. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.06.014

国家自然科学基金资助项目(51105209，61401211，51175267)；中央高校基本科研业务费专项资金资助项目(30915118804)；江苏省高校自然科学研究重点资助项目(15KJA460004)；高等学校学科创新引智计划资助项目(B16025);航空科学基金资助项目(20161959001)

2016-02-29；

2016-06-07

TP3

崔兴梅，女，1992年2月生，硕士生。主要研究方向为结构健康监测、无线传感器网络。曾发表《A novel RFID-based sensing method for low-cost bolt loosening monitoring》(《Sensors》2016,Vol.16,No.2)等论文。

E-mail: 114101000159@njust.edu.cn

吴键，男，1979年11月生，副教授。主要研究方向为无线传感器网络。

Ε-mail:wuj@njust.edu.cn

欢迎订阅《振动、测试与诊断》

《振动、测试与诊断》由工业和信息化部主管，南京航空航天大学和全国高校机械工程测试技术研究会联合主办，是反映振动、动态测试及故障诊断学科领域的科研成果及其应用情况的技术性刊物。主要刊登国内外以振动测试与故障诊断为中心的动态测试理论、方法和手段的研究及应用方面的技术文献，包括实验测试技术、测试仪器的研制、方法和系统组成、信号分析、数据处理、参数识别与故障诊断以及有关装置的设计、使用、控制、标定和校准等，不拘泥于行业和测试项目。

本刊为EICompendex数据库收录期刊和中文核心期刊，双月刊，每逢双月末出版，每本定价30元，全年180元。欢迎订阅和投稿，欢迎在本刊刊登各类广告和科技信息。

编辑部地址：南京市御道街29号 邮政编码：210016 电话：(025)84893332

传真：(025)84893332 E-mail:qchen@nuaa.edu.cn 网址：http:∥zdcs.nuaa.edu.cn