高精度定位平台X-Y方向振动误差补偿

刘吉柱, 张雯雯， 陈立国， 潘明强， 王阳俊

(苏州大学机电工程学院&苏州纳米科技协同创新中心 苏州，215021)

高精度定位平台X-Y方向振动误差补偿

刘吉柱, 张雯雯， 陈立国， 潘明强， 王阳俊

(苏州大学机电工程学院&苏州纳米科技协同创新中心 苏州，215021)

为了减小定位平台在X，Y方向的振动误差，实现高精度定位，搭建了宏微结合精密定位系统，由高性能直线电机驱动，气体静压导轨支撑和导向的宏动平台实现系统的大行程微米级定位，并由安装在宏动平台上的压电陶瓷驱动的微动平台对系统进行定位精度补偿。建立了定位系统机电耦合振动模型，采用比例积分微分(proportion integral derivative, 简称PID)控制与最小节拍响应控制相结合的策略控制宏动平台，采用前馈-PID控制驱动微动平台，通过电容式微位移传感器实时检测定位系统终端的位置输出信号作为微动台的输入信号，实现定位系统的闭环反馈控制，达到宏动平台的振动误差实时补偿的目的。实验结果显示，所设计的微动补偿平台具有良好的动态特性，定位系统具有良好的误差实时补偿效果，针对X，Y向的振动范围由补偿前的4和3.5μm，补偿后减小到1μm的范围内。结果表明,所研究的振动误差补偿方法可以有效减小定位系统的振动误差，提高系统的定位精度。

宏微定位平台；振动模型；压电陶瓷；误差补偿

引 言

随着微观领域研究的不断深入，对定位精度要求也不断提高。定位平台在具有一定运行速度、保证运行效率的基础上同时要求具有微米级、纳米级的定位精度[1]，通过对定位误差进行补偿来提高定位系统的性能是当今高速精密定位系统的关键技术。但是针对振动扰动对定位平台定位精度的影响及振动的抑制研究还存在很多理论和实际问题，所以研究振动对定位平台的微扰动机理和振动误差补偿控制方法具有重要的理论和实用价值。

在高精度定位平台方面，国外出现了不同形式的精密定位平台发展产品[2]，例如美国的Intel、日本的佳能及NSK公司、德国的PI、韩国电子技术研究所等都研究开发出了各具特色的定位平台，在定位平台机构形式、驱动方式和控制方法上优化了传统的定位平台。近年来，日本东京工业大学采用“直流电机+丝杆”驱动方式，利用空气静压轴承和气浮导轨导向的机构，达到±2nm的定位分辨率，提高了该系统的定位精度[3]。在国内，哈尔滨工业大学运用音圈电机驱动宏动平台，压电陶瓷驱动微动平台，其优点是采用闭环控制，运用双光栅跨尺度位移测量方法，在20mm的行程范围内达到10nm的运动分辨率；缺点是整个系统结构复杂。[4-5]关于提高精密定位系统精度的研究主要是误差防止法和误差补偿法，其中误差补偿法最为关键，得到了一些成果[6-8]。

宏动平台在工作运转时，直线电机电磁推力会产生波动，从而影响电机性能，产生振动和噪声，造成了工作台在x,y方向产生振动的现象。针对此现象，笔者提出了基于微动工作台、采用实时补偿振动误差的闭环控制方案，最后进行了实验验证。

1 定位平台振动误差分析与建模

1.1 定位平台振动误差来源分析

图1所示为高速精密定位系统宏动工作台的三维模型。定位系统的驱动机构传统方式常采用旋转电机通过联轴节带动滚珠丝杠驱动工作台的形式，其在传动时的运动间隙、相互摩擦和接触时产生的热变形及振动都会造成系统定位精度的降低。笔者所设计的平台采用高速、高精度和高可靠性直线电机的驱动方式，取消了驱动机构到末端执行器的中间所有传动环节，避免了中间环节带来的负面影响。由于气体静压导轨具有无摩擦磨损、较高的稳定性等优点，所以平台上、下直线运动轴采用超精密气体静压导轨。平台在X轴运动滑块副和Y轴运动平台上分别配置高分辨率以及高速响应的直线光栅线位移传感器来实现位置和速度的闭环测量控制。

图1 高精度定位系统宏动平台Fig.1 High precision positioning system of macro platform

定位平台在工作环境中运动时，由于内外振源的影响会产生振动误差，从而影响平台的定位精度。电机运转时直线电机的电磁推力所产生的波动，是导致振动误差的主要原因。

所有振动产生的因素中，直线电机电磁推力产生的波动以及直线电机动子与定子之间法向力的波动会使得电机产生振动和噪声，也是最终导致定位平台产生X,Y方向振动误差的主要原因，如图2所示。

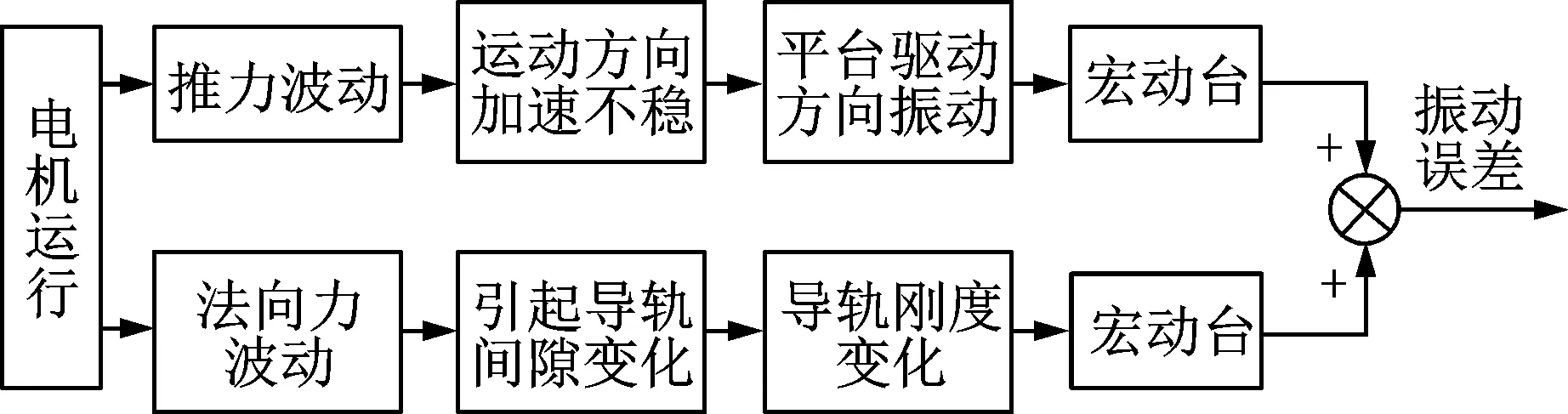
图2 振动误差主要来源方框图Fig.2 Main source block diagram of vibration error

直线电机电磁推力产生的波动会导致运动方向加速不稳，从而导致平台驱动方向产生振动。在一些高速高精密场合下，由于直线电机产生高频率法向吸力，会使整个系统产生振动，从而造成导轨的支撑导向性能下降，最终影响系统的性能。

笔者设计的定位平台要求其在上、下轴行程分别在600和400mm的同时定位精度优于1μm。

1.2 X方向振动误差建模

为了研究X方向上精密定位平台的性能，在高动态下，将微位移机构和气体静压导轨滑块副作为柔性环节，建立了X轴振动模型，其物理模型简化如图 3 所示。其中：Kx1为X轴直线电机的伺服刚度；Kx2为Y轴承载平台气体静压导轨滑块副的侧向等效接触刚度；Kx3为X轴振动定位平台中双层弹性平行板铰链的刚度与压电陶瓷刚度之和；Cx1为X轴直线电机的等效阻尼系数；Cx2为Y轴承载平台气体静压导轨滑块副的等效阻尼系数；Cx3为双层弹性平行板的等效阻尼系数；Mx1为X轴双排直线电机动子、X轴宏动平台及其附属构件等效集中质量；Mx2为Y轴承载平台及其附属构件等效集中质量；Mx3为振动平台及其附属构件的等效集中质量；Fx1为X轴直线电机的驱动力；Fx3为压电陶瓷的驱动力；μx1为X轴气体静压导轨滑块副的等效摩擦因数，其值很小，可忽略不计。

图3 X轴平台振动物理模型Fig.3 X axis platform vibration physical model

经过推导，平台X轴运动微分方程为

(1)

1.3 Y轴定位平台振动误差模型

为了研究高速、高加速情况下精密定位平台系统的动态特性，将弹性解耦机构以及直线导轨滑块副和微位移机构作为柔性环节，建立了Y轴振动模型，物理模型简化如图4所示。其中：Ky1为Y轴直线电机的伺服刚度；Ky2为微位移机构中双层弹性平行板铰链的刚度与压电陶瓷刚度之和；Cy1为Y轴直线电机的等效阻尼系数；Cy2为双层弹性平行板的等效阻尼系数；My1为Y轴直线电机动子、导向滑台及其附属构件等效集中质量；My2为振动平台及其附属构件的等效集中质量；Fy1为Y轴直线电机的驱动力；Fy2为压电陶瓷的驱动力；μy1为Y轴气体静压导轨滑块副的等效摩擦因数，其值很小，可忽略不计。

图4 Y轴平台振动物理模型Fig.4 Y axis platform vibration physical model

根据牛顿第二定律，可得Y轴平台运动微分方程为

(2)

1.4 X轴和Y轴机电耦合数学模型的建立

排除外界环境对平台的干扰，为进一步简化分析，平台的动力学模型可描述为

(3)

其中：M为驱动平台的质量；μ为气体沿运动方向的等效阻尼系数；FL为负载力；F(t)为电机驱动力；Ke为反电动势常数；Li，Ii，Ri分别为线圈的电感、电流和电阻；U为输入电压；Kf为机械电磁能量转换常数。

由式(3)进一步可得

(4)

通过拉氏变换，传递函数为

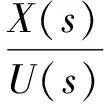
(5)

系统的具体参数如表1所示。

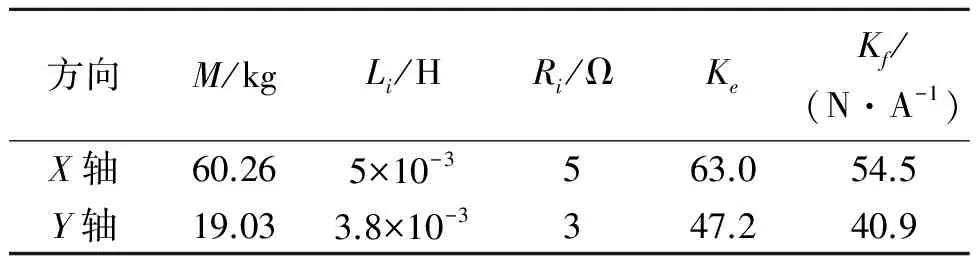
表1 定位平台X轴和Y轴各参数

由于电磁时间常数Li/Ri相对于电磁能量转换常数Kf很小，所以为简化运算可忽略不计。同时，气体静压等效阻尼系数μ可以忽略，将X轴和Y轴各参数分别代入上式，可得电压-位移的传递函数。伺服驱动器的功能是把输出电压转换成电流来驱动电机，所以最终得电流-位移的传递函数为

G(s)=0.9/(s2+0.9)

(6)

G(s)=2.15/(s2+2.15)

(7)

2 定位平台响应特性分析

电机高加速启停带来的宽频微振动以及外界环境影响下对定位平台带来的振动影响都使得定位系统的定位精度和系统稳定性受到影响。基于宏动控制系统振动机理及其机电耦合模型，采用传统PID控制，加入前置滤波器，并采用最小节拍响应控制来调整参数的组合控制策略[9]，提高系统的稳定性。图5所示为宏动系统机电耦合控制系统方框图，其中：Gp(s)为前置滤波器的传递函数；Dp(s)为控制器传递函数；Gc(s)为被控对象的传递函数。

图5 宏动系统总体控制方框图Fig.5 Overall control block diagram of macro motion system

为了验证所设计的控制方法的正确性，对系统进行仿真，分别得到X，Y轴的阶跃响应曲线，如图6所示。

图6 定位平台阶跃响应曲线Fig.6 Positioning platform step response curve

由图可知，定位平台在给定1mm位移阶跃信号响应下，X和Y轴的稳定时间都约为18ms左右，由于X轴负载Y轴平台及其附属机构，使得X轴惯性更大，在起始阶段的响应没有Y轴快。由于X，Y轴直线电机采用的是同一系列型号、行程有所不同的无铁芯直线电机，所以整体响应相近，基本上没有稳态误差，表明定位平台能够进行高加速启停的往复平稳运动。

3 微动补偿平台的设计与分析

3.1 微动补偿平台的设计

为了实现微动误差补偿机构的一系列精度高、重量轻、响应快及位移输出特性好等指标要求[10]，笔者设计了双层平行板柔性铰链，它能够连接各个部件，其三维模型如图7所示。

将负载平台视为刚体，可得平行板铰链刚度公式为

(8)

其中：F为外界激励；b，L，t分别为弹性梁的宽度、长度、厚度；E为弹性梁材料的弹性模量。

3.2 微动补偿平台有限元分析

在ANSYS里建立有限元分析模型，先赋材料属性，此处选用硬铝2A12，然后划分网格，最后仿真分析静态输出位移和应力分布情况。图8所示为仿真结果。

图8 位移、应力有限元模型云图Fig.8 The finite element model of displacement and stress

为了实现其在满足输出位移的基础上，提高固有频率，增强抗振能力，本研究压电陶瓷采用德国米依公司内部集成应变片传感器的PSt150/5×5/20型压电陶瓷致动器，它的优点是能够有效消除压电陶瓷输出的非线性影响，实现机构的驱动、检测一体化。

各柔性铰链可近似看作弹簧，所以简化了整个微动平台系统，其微动台的运动微分方程为

(9)

其中：m为工作台的质量；μ为弹性铰链平行板的阻尼系数；K为平行板柔性铰链刚度；Kp为压电陶瓷驱动器刚度；x为工作台的输入位移；y为工作台的输出位移。

式(9)经拉氏变换可得

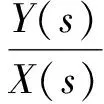
(10)

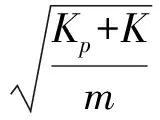
4 控制方法的研究

4.1 前馈-PID混合控制方法

传统PID控制一定程度上能够提高定位系统的定位精度，若想进一步提高系统的响应速度、重复定位精度等动静态性能指标，通常需要结合其他控制算法混合控制，达到优势互补，更进一步提高系统的综合特性。国内外学者也做了大量研究，如设计单神经元自适应PID控制器、电荷控制方法及各类迟滞模型等，虽然改善了迟滞蠕变等非线性现象，但也增加了控制计算量。针对振动台致动器压电陶瓷输出的迟滞非线性影响补偿定位精度的问题，笔者采用前馈-PID(比例、积分、微分)控制相结合的控制方法，有效抵消了压电陶瓷迟滞非线性给振动补偿机构的定位精度带来的影响。

图9所示为基于前馈-PID混合控制的复合控制系统方框图，该系统主要由控制计算机、A/D和D/A转换器、集成高压运放电路的压电陶瓷驱动电源、压电陶瓷驱动的振动补偿机构以及电容测微仪组成的闭环反馈系统。

该复合控制过程主要为：给定位移由计算机算得；前馈控制输出控制电压信号及压电陶瓷输出位移是经过D/A转换器和集成在压电陶瓷驱动电源内的运放电路驱动得出，并通过电容测微仪测头检测由压电陶瓷驱动的振动补偿机构的输出位移；偏差信号是通过A/D转换器和电容测微仪控制电路，将输出信号反馈回控制计算机，然后与输入信号进行对比，该信号经过PID控制器联合运算，输出一个位移补偿控制量，用于补偿压电陶瓷本身迟滞、蠕变等非线性影响以及外界环境(包括宏动系统内外振源及系统外界环境)对振动补偿机构造成的影响而产生的误差。在混合控制过程中，反馈信号经过PID控制运算，不断与输入信号进行比较，直至偏差信号e(kt)达到所要求的范围内。

复合控制中，控制系统的信号为

u(kt)=ud(kt)+Δu(kt)=ud(kt)+kpe(kt)+

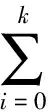
(11)

其中：t为系统的采样周期。

通常情况下，为保证系统具有足够的精度，采样周期必须足够小。

4.2 微动系统阶跃仿真分析

根据前人实践总结的经验，最终确定本研究设计的PID控制器的3个参数分别为：kp=3.5，TI=2 000，TD=0。图10所示为微动控制系统前馈-PID混合控制算法与单纯的PID控制下的阶跃信号响应仿真图，输入测试阶跃信号的峰值为15 μm，频率为20 Hz，采样时间为0.3 ms。

图10 前馈-PID控制与PID控制阶跃仿真对比图Fig.10 Comparison of the step simulation of feed forward PID control with PID control step simulation

仿真结果表明，前馈-PID混合控制方法相比传统经典PID控制效果要好，动态响应更好，稳态误差得到提前抑制，体现了前馈控制效果，同时超调量减小，系统的动态响应速度更快，精度更高。

5 振动误差补偿实验

高速精密定位平台振动误差补偿实验系统如图11所示。

图11 高速精密定位平台振动误差补偿系统Fig.11 High speed precision positioning platform vibration error compensation system

基于宏微结合控制方法的原理为：通过上位机对宏动控制器施加目标位移指令，宏动控制器按照控制算法控制宏动平台最终定位，通过光栅尺进行目标位置反馈，当宏动台末端位置进入压电陶瓷驱动的微动平台的工作补偿范围内，微动控制器将通过电容测微仪检测微动台的位移信号与光栅尺反馈的宏动台的位移信号，按照控制算法进行运算作为微动系统的输入信号，最终通过微动控制器控制振动误差补偿系统对定位系统的振动误差进行实时误差补偿，达到纳米级的定位。通过安装在高速精密定位系统末端位置的电感测微仪来实时监测宏动定位平台在振动误差补偿前后的振动特性情况。

针对X轴平台进行振动误差补偿实验时，为减小干扰，X轴误差补偿实验时需锁定Y轴平台，同时定位平台在行程范围内按规划轨迹运动。图12为X轴振动误差补偿前后的实验曲线图，左图为振动误差补偿前系统末端点的振动误差曲线，X轴振动误差的振动范围约为4μm；右图为振动误差补偿后系统末端点的振动误差曲线，其结果由宏动定位平台与振动误差补偿平台的运动叠加而成。由图12可知，整个定位平台的振动误差范围约为0.9μm。

图12 X轴振动误差补偿前后曲线Fig.12 Before and after the vibration error of X axis compensation curve

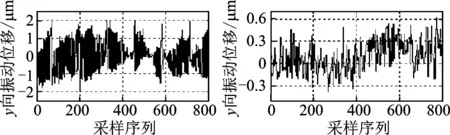
图13 Y轴振动误差补偿前后曲线Fig.13 Before and after the vibration error of Y axis compensation curve

针对Y轴平台进行振动误差补偿实验时，为减小干扰，Y轴误差补偿实验时需锁定X轴平台，同时定位平台在行程范围内按规划轨迹运动。图13为Y轴振动误差振动补偿前后振动曲线图，左图为进行振动误差补偿前系统末端点的振动误差曲线，Y轴振动误差的振动范围约为3.5μm；右图为进行误差补偿后系统末端点的振动误差曲线，振动误差范围减小，约0.9μm。

6 结束语

针对所搭建的宏微结合定位平台系统，采用“直线电机+压电陶瓷”驱动，运用电容测微仪进行闭环控制，反馈位置信息。采用前馈PID控制算法来实时补偿振动误差。通过实验研究，系统的工作行程为400mm×600mm，它的定位平台的精度优于1μm，从而验证了所设计的基于误差补偿方法的定位系统能够满足实现高精度定位的条件。

[1] 林海波，杨国哲，黄小良.大行程超精密工作台的研究[J]．机械设计与制造,2010, 6(6): 130-131.

Lin Haibo, Yang Guozhe, Huang Xiaoliang. Design of a large travel ultra precision stage[J]. Machinery Design & Manufacture,2010, 6(6): 130-131.(in Chinese)

[2] Yun Yuan,Li Yangmin .Design and analysis of a novel 6-DOF redundant actuated parallel robot with compliant hinges for high precision positioning[J]. Nonlinear Dyn, 2010, 61(1): 829-845.

[3] Mao Junhong ,Tachikawa H ,Shimokohbe A . Precision positioning of a DC-motor-driven aerostatic slide system[J]. Precision Engineering, 2003, 27(1): 32-41.

[4] 节德刚.宏/微驱动高速高精度定位系统的研究[D]. 哈尔滨：哈尔滨工业大学, 2006.

[5] 节德刚，刘延杰，孙立宁,等，一种宏微双驱动精密定位机构的建模与控制[J].光学精密工程, 2005, 13(2): 171-178.

Jie Degang, Liu Yanjie, Sun Lining, et al. Modeling and control of a macro-micro dual-drive ultra-precision positioning mechanism[J]. Optics and Precision Engineering,2005, 13(2): 171-178.(in Chinese)

[6] Ferrerira P M, Liu C R. A method for estimating and compensating quasistaric error of machinetools[J]. Journal of Engineering for Industry, 1993, 115(1): 149-159.

[7] Veldhuis S C, Elbestawi M A. A strategy for compensation of errors in five-axis machining[J]. Annals for CIRP, 1995, 44(1): 373-377.

[8] 孙麟治，李鸣鸣，程维明.精密定位技术研究[J]. 光学精密工程, 2005，13(S): 69-75.

Sun Lingzhi, Li Mingming, Chen Weiming. Study on precision positioning technique[J]. Optics and precision engineering,2005，13(S):69-75.(in Chinese)

[9] 郭劲,王卫兵,陈娟,等. 最小节拍组合控制方法在光电跟踪系统中的应用[J].光学精密工程,2013，10:2594-2602.

Guo Jing, Wang Weibing, Chen Juan, et al. Application of minimal prototype control method in opto-electronics tracking system[J]. Optics and Precision Engineering,2013，10:2594-2602.(in Chinese)

[10] 马立,谢炜,刘波,等. 柔性铰链微定位平台的设计[J]. 光学精密工程,2014(2):338-345.

Ma Li, Xie Wei, Liu Bo, et al. Design of micro-positioning stage with flexure hinge[J]. Optics and Precision Engineering,2014(2):338-345.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.06.024

高等学校博士学科点专项科研基金资助项目(20133201130003)；国家高技术研究发展计划(“八六三”计划)资助项目(2013AA041109)

2016-01-16

2016-03-18

TH162

刘吉柱，男，1978年8月生，博士、副教授。主要研究方向为机电一体化技术、电机及驱动控制技术。曾发表《Selecting of the temperature measurement points for positioning platform with large trip and high precision thermally induced error compensation model》(《Applied Mechanics and Materials》2013,Vol.431)等论文。

E-mail: liu_jizhu@163.com

王阳俊，男，1979年11月生，博士、讲师。主要研究方向为超精密测量技术。

E-mail: wangyangjun@suda.edu.cn