不同外激励参数下射流的附壁振荡特性

2018-01-04邹久朋刘学武代玉强李俊龙

振动、测试与诊断 2017年6期

关键词：总压射流矩形

邹久朋，刘学武，程蛟，代玉强，李俊龙

(大连理工大学化工机械与安全学院大连，116024)

不同外激励参数下射流的附壁振荡特性

邹久朋，刘学武，程蛟，代玉强，李俊龙

(大连理工大学化工机械与安全学院大连，116024)

为获得新型外激励振荡器的振荡性能跟随外激励流参数和时变模态的改变而变化的规律和敏感性，为该振荡器的高效应用提供依据与参考，采用计算流体动力学(computational fluid dynamics，简称CFD)数值模拟和实验的方法，对激振能力和振荡射流的总压保持率K的变化进行了考察。结果表明：总压保持率K随外激励流总压的降低而减小；非激励侧泄漏的激励流也使K略降，但却显著降低了激振能力；而激励流占空比减小即提前关断，会显著降低振荡射流总压保持率；激励流起始压力渐升的影响较小，而中后期压力丧失或渐降，会使K有较大跌落。研究证明，外激励振荡器对激励流参数的变化具有较强的适应性，20%以内的变化不影响振荡稳定，仍能维持较高的总压保持率K，可振区间内最低K比现有的自激励振荡器高出10%以上。

射流；附壁振荡；外激励；总压保持率

引言

不可压缩脉冲射流的研究应用已十分广泛[1]。借助于Coanda效应和自激励机制，实现附壁切换的摆动振荡射流，也可用于流量计量[2]、分配脉冲到各根气波管的静止式气波制冷机[3]等。近年来，以振荡或合成射流控制降低流动边界层分离[4]、提高机翼升力[5-6]等，已成为高速流动控制领域的研究热点。自激励附壁振荡射流虽实施简单，但机理分析、数值模拟和实验皆表明，音波式、共鸣腔式、反馈式及负载式[7-8]等自激励方式，稳定振荡所对应的振荡器几何参数与流体工况范围比较小，振荡可靠性差。振荡过程效率指标总压保持率K(振荡射流总压与来流总压之比)仅达62%～75%[9]，且振荡频率和对称性很难控制，这些都阻碍了射流技术向更多领域拓展应用。为减小射流振荡能量损失，必须提高激励流总压，对后续主射流提供持续的激励推动力。仅靠主射流分流反馈的自激励，无论以何种方式，上述两条件都无法满足。若取与主射流同源小股流体，切换调制成两股交替脉冲流，从两侧引入振荡腔代替自激励，可满足上述两项条件，提高射流振荡器的效率。数值模拟和实验研究表明，只需引入不到10%主射流流量的外激励流即可稳定振荡，且频率任意可调，其最大优点是损失要比自激励小许多，总压保持率K普遍可达85%，尺寸优化的振荡器能达90%[9-10]。

以上研究是基于外激励流总压峰值与主射流相等，且持续近半周期，时变特性也是较理想的突升突降模态。实际应用中，切换生成的外激励流难以达到理想状态，将导致射流附壁振荡特性和能效指标变差。笔者系统研究了外激励流峰值总压改变、一侧激励流在非激励期间未关严漏气、激励流提前关断、激励流总压缓升、缓降和激励频率大幅变化等多种情况下，主射流附壁振荡的响应特性。研究确定了激励条件的改变对射流外激励振荡关联影响的敏感性程度和外激励流可行变化与弹性操作范围，可为外激励振荡器的实际应用提供依据与参考。

1 CFD数值模拟和实验

1.1 计算模型与性能指标

外激励振荡器[11]的基本结构如图1(a)所示。与主射流同源的小股外激励流体，被分成两股相位差为T/2的脉冲流，分别通过两边宽度为b的激励流入口，交替进入振荡腔，激励主射流切换附壁振荡。计算流体力学的计算机工程与制造集成程序(integrated computer engineering and manufacturing code，简称ICEM)结构化网格划分如图1(b)所示，独立性分析确定网格最大尺寸为0.2 mm，将喷嘴附近网格加密，沿流动方向渐疏。图1中：W为主射流喷嘴出口宽；S为位差；L为直段长；b为激励口宽；h为激励口距；H为劈距；θ为劈张角。

振荡器性能指标包括振荡指标和能效指标，振荡指标指维持稳定振荡所需的最小激励流用量比J=Qmin/Qj，Qj为主射流流量。若流道深度相等，J可用流道的宽度比b/W近似代替。能效指标用振荡器分支出口总压时均值Po与振荡器入口总压Pi的比值K来衡量(包括喷嘴流动损失)，称为总压保持率[10]，K越接近于1，损失越小，出口静压一定，则流速越高。

对Po的求算过程为：将分支流出半周期的各个Δt时段，对出口各网格流出的质量流量与网格节点总压的乘积积分，再除以半周期内总的质量流量得到Po，即

(1)

其中：ptk为分支出口截面第k个网格外边界节点总压。

由于总压内包括动能，与质量关联，因此须对质量加权积分。笔者考察在各种不同的外激励流参数与模态下性能指标的响应特性与规律。为兼顾普遍性，选择一组几何参数较优化的振荡器为研究对象，其尺寸为：喷嘴出口宽W=2.5 mm；劈距H/W=6.4(H=16 mm)；位差H/W=0.4(H=1 mm)；直段长L/W=1.2(L=3 mm)；垂直激励口距h/W=0.7(h=1.75 mm)；激励口宽b/W=0.2(b=0.5 mm)；实验模型的流道深度为9 mm。

以往的数值模拟和实验结果皆表明，在近似矩形的梯形时变激励条件下，该振荡器振荡稳定，总压保持率K在85%左右。将此激励条件下的振荡性能和能效指标作为基准，考察激励流参数和模态改变之后，振荡和能效指标相对于该基准值的变化程度和规律。取振荡器入口总压Pi=0.36 MPa，温度为300 K，出口静压Pos=0.18 MPa，介质为空气，黏度为1.789 4×10-5kg/(m·s)，其余均为固壁边界。

1.2 数值求解方法

主射流宽度越窄，越容易激励和附壁，故振荡器流道的深度远大于其宽度，流道上下边界的影响很小。对振荡器分别采用二维和三维CFD模拟试算，相差均在2%以内。因此采用二维模拟，可节省大量用时。

振荡器内为超音速，可压缩强湍流流动，求解时采用均Navier-Stokes方程的Reynolds平均法[12]。由于喷嘴射流湍流的各向异性，采用两方程Realizablek-ε湍动涡黏模型，以有限体积法对控制方程进行离散。扩散项采用计算效率高、二阶精度的中心差分格式，收敛较快。对流项为各向异性，为避免数值振荡，采用迎风格式中的Roe通量差分分裂格式进行离散[13]，以二阶隐式时间步进行迭代。

1.3 实验装置流程与测量

实验流程如图2所示。

1-压缩机；2-贮气罐；3-控制阀；4-外激励流换向调制阀；5-激振器；6-功率放大器；7-信号发生器；8-外激励射流振荡器；9-压力变送器(共3只)；10-计算机图2 外激励振荡器实验流程Fig.2 Experimental flow chart of external excitation oscillator

振荡器实验模型为3层结构：下层做支撑；中层加工振荡器流道；上层导入进气和激励流，并设测压孔。中层厚即流道深度为9 mm，各流道宽度尺寸与模拟计算取值一致，并用钢片塞尺测量和精确修正。

外激励流换向调制阀为双向圆锥阀芯往复运动结构，以往复激振器驱动。信号发生器产生可调频率和波形信号，送功率放大器放大后作为激振器的动力电源。

3只压力变送器分别测量振荡器入口压力Pi、激励流入口压力PA和振荡器分支出口压力Po。用4路同步800 kHz采样频率的高速PIC总线A/D转换卡进行计算和数据采集。

由于分支流道超音速脉冲流动动压很难等熵转换到总压，也就很难测准，流道内添加取压孔会产生激波损失，并使振荡特性变坏。因此，对Po的测量，在出口外10 mm，测量出口脉冲射流静压,采用冲力法实施。由于分支出口有过膨胀的复杂波系，因此将测量位置固定，如此可较准确测量Po相对变化的增量。

2 模拟和实验结果对比与分析

2.1 激励流总压峰值变化对振荡性能的影响

保持振荡器入口总压、出口静压不变，以及激励流梯形波模态、频率f=50 Hz、波谷压力0.18 MPa不变，只改变峰值(平台)总压，从标准值的120%起逐步减小，直到主射流不能稳定振荡为止。模拟计算和实验测得的总压保持率K(K1)随激励流总压峰值Ph的变化关系如图3所示。实测值之所以用K1表示，是因实测出口总压达不到振荡射流的滞止压力，而模拟算得的总压为滞止压。

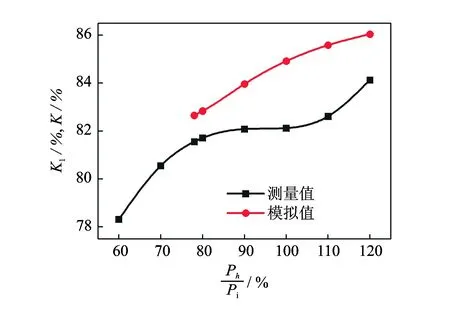
图3 K(K1)与Ph的关系曲线Fig.3 Correlation curves between K(K1) and Ph

可以看出，若激励流总压峰值Ph超过主射流总压20%，总压保持率K可上升1.5%～2%，表明外激励流的多余能量可汇入振荡射流，与之前的相关研究结论一致；而Ph降低，就须靠主射流挟带增速，如喷射器抽吸低压流体那样消耗主射流动能；当Ph下降20%，K也降低约2%。

激励流压力降低，质量流量也减小，激励压差和动量的双重减少导致振荡衰弱。数值模拟Ph小于主射流总压的78%，已不能维持稳定振荡，需增大激励口宽b/W以增加激励流量，振荡才能维持。随激励流峰压Ph百分比的降低，所需最小口宽b百分比增幅的模拟结果如图4所示。随激励流压力百分比的减小，所需激励口宽b呈指数式增大。

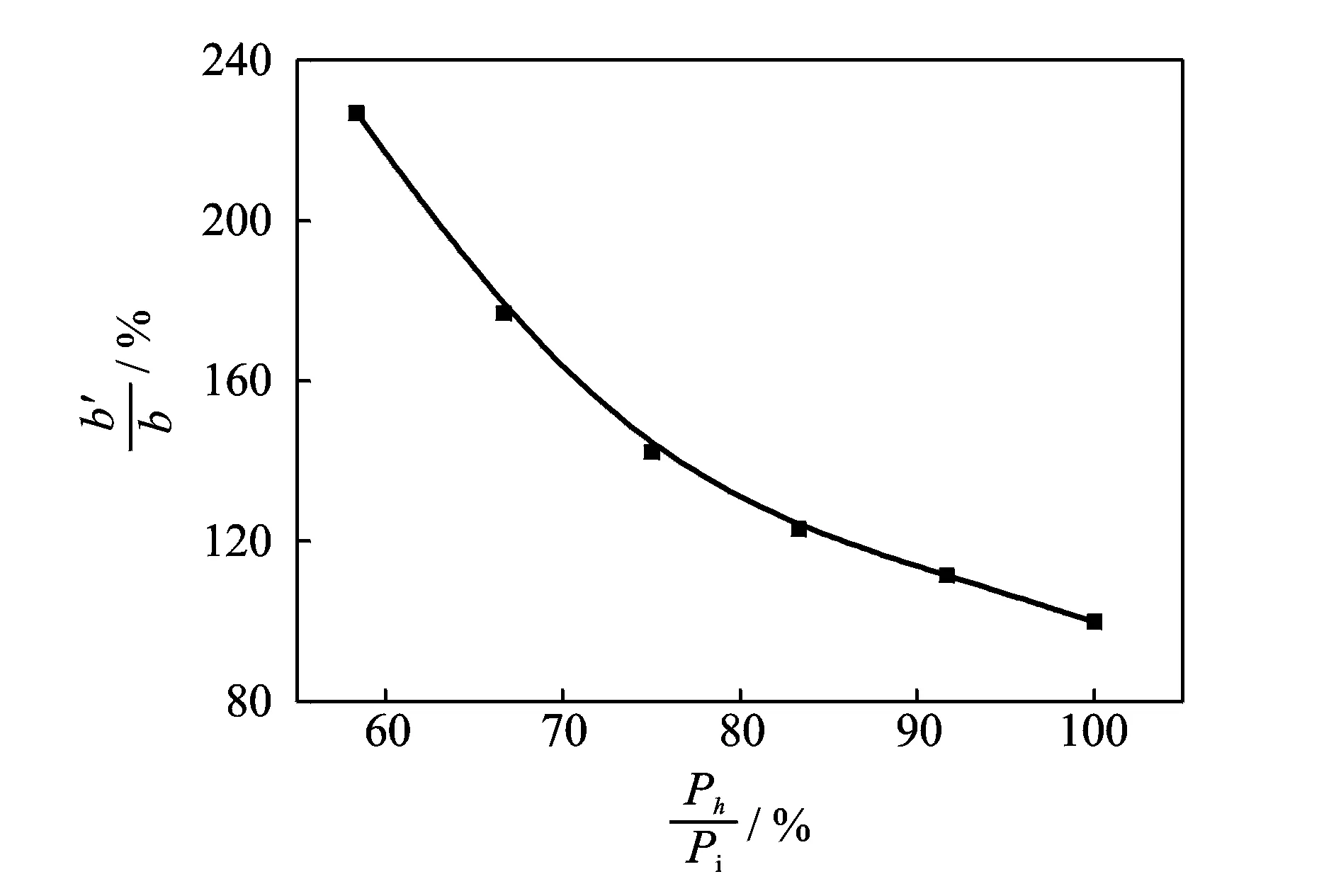
图4 最小激励口宽b与Ph的关系曲线Fig.4 Correlation curve between b and Ph

实验研究发现，将激励流总压Ph调低到主射流的58%左右，振荡才停止，远低于数值模拟值78%。分析很可能是激励流被关闭瞬间，该侧激励流道内产生较强的膨胀波向激励口传播，其低压“吸拽”作用与对侧启动的激励流的推力相叠加，而数值模拟没有设置这个低压。因此，考察是否振荡，模拟结果是偏安全的。

2.2 非激励侧泄漏激励流对振荡性能的影响

理想情况下，当非激励侧的那股激励流被截止，该激励口附近静压与振荡腔平衡，但调制装置实际可能的泄漏，导致仍会有激励流进来，使非激励侧压力升高。保持激励流峰值压力Ph不变，逐步升高波谷压力PL，以模拟非激励侧有流体漏入的情况，得到总压保持率K与PL增幅百分比的关联曲线如图5所示。

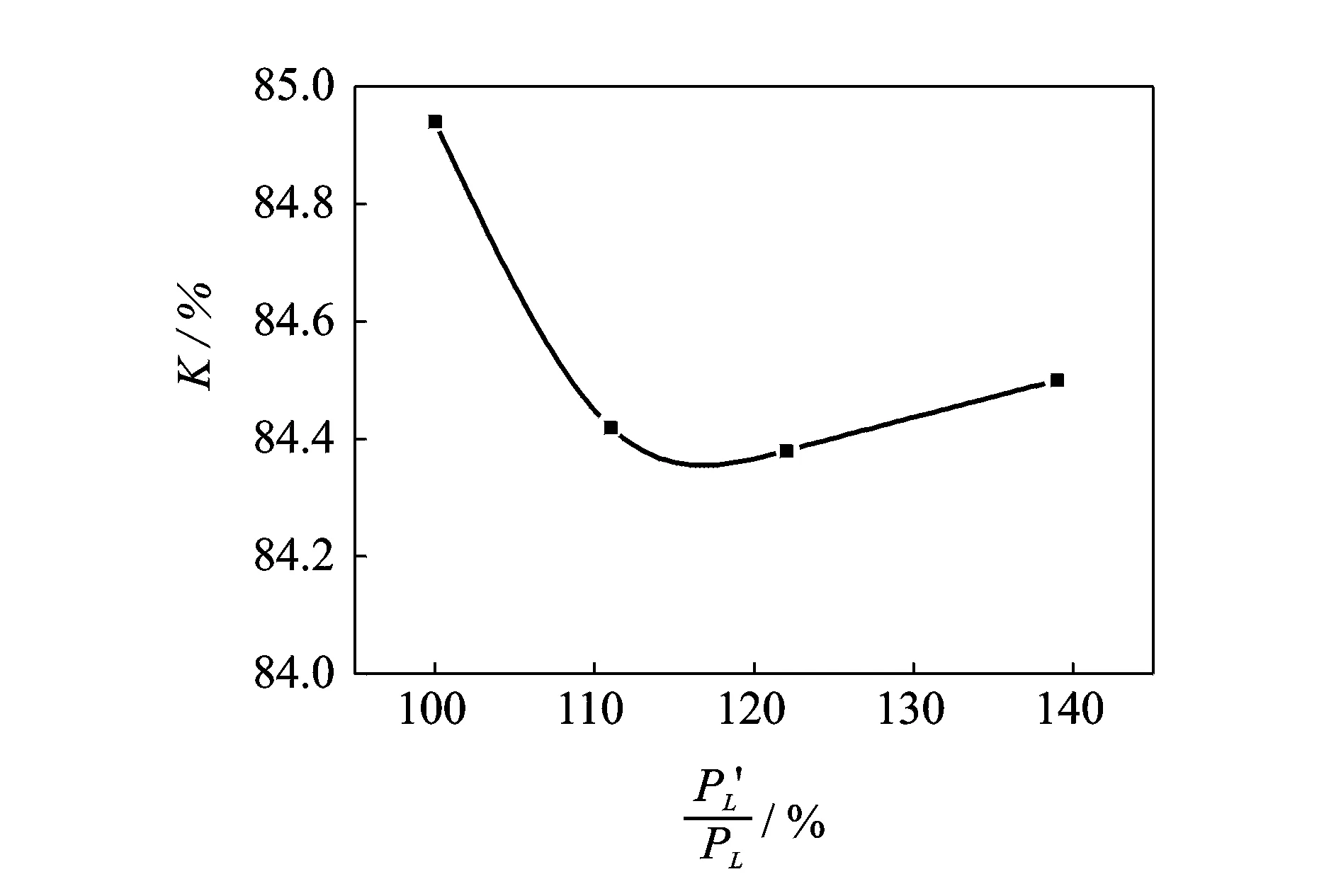
图5 K与PL增幅百分比的关联曲线Fig. 5 Correlation curve between K(K1) and ratio of percentage increase of PL

随PL的升高，总压保持率呈先降后缓升趋势，但变化不足1%。泄漏进来的激励流总压低于主射流，被卷吸而消耗主射流动能，使K下降，但随其压力上升，喷射器效应减弱，总压保持率K略有回升。激励压差推动力随PL升高逐渐减小。模拟表明，当PL增幅超过50%，已不能激励主射流切换振荡。

还有一种情况是两侧激励流时间重叠，一侧流动还未关严，另一侧已开启，其影响与PL升高相仿。

2.3 激励流占空比减小对振荡性能的影响

若换向调制器提前关闭激励侧的外激励流，由于康恩达(Coanda)效应，主射流会继续保持附壁。但由于缺乏后续的激励压差和动量，其后主射流的偏转将完全依靠主射流卷吸附壁侧形成旋涡低压区的吸拽，如同自激励附壁那样，会损失主射流较多的能量。

其他条件不变，逐步减小外激励流峰值的占空比，即提前关闭，振荡器分支出口振荡射流的总压保持率随占空比变化的曲线如图6所示。在射流附壁期间，全程保持和后半时段关闭激励流，即占空比D分别为50%和25%，出口总压波形的变化如图7所示。

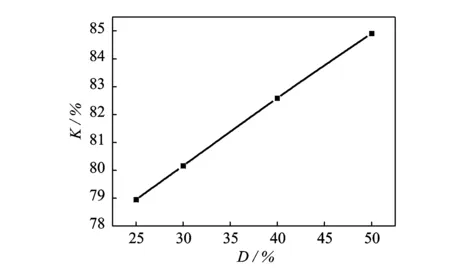
图6 K与D的关联曲线Fig.6 Correlation curve between K and D

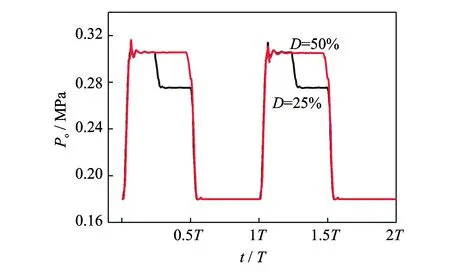
图7 不同占空比D对应的出口总压波形 Fig.7 Outlet total pressure waveform corresponding to different D

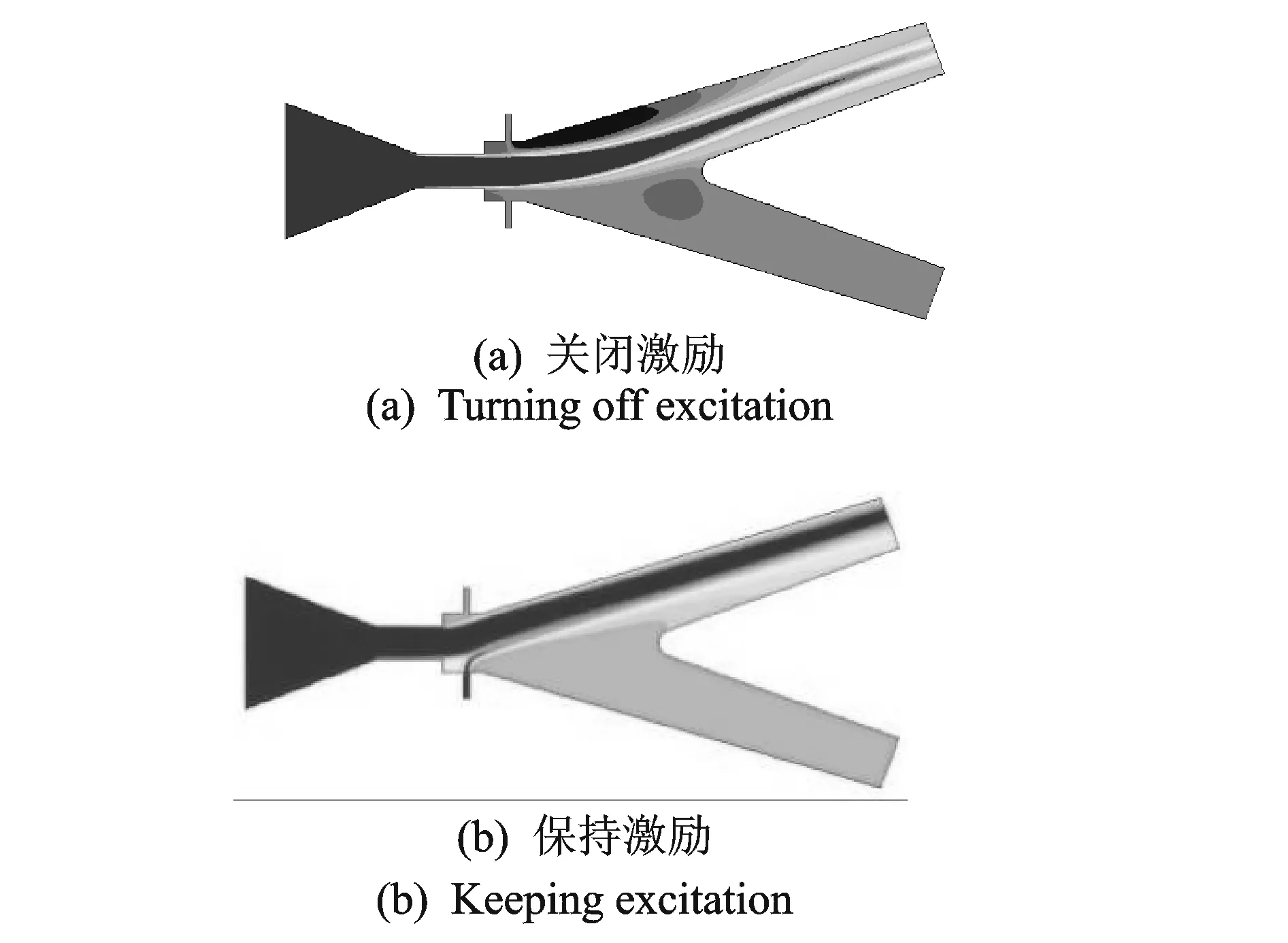
图8 附壁总压云图Fig.8 Nephogram of total pressure of attached to the wall

总压保持率K随占空比D的减小而线性下降，占空比减小一半(50%～25%)，K降低约6%。从图7可知，激励流一消失，出口振荡射流的总压就立即下降10%左右。消失的越早，出口的时均总压就越低。

从模拟流场总压云图可知，激励流提前消失后，康恩达效应保持的附壁状态如图8(a)所示，与激励流持续激励的附壁状态图8(b)所示显著不同。后者主射流完全贴附于分支流道的外侧，几乎没有旋涡区和增厚的边界层，而内侧也被持续的激励流所填充，没有边界层分离现象；而前者主射流和附壁之间一定有低压旋涡区的存在，主射流两边的边界层增厚，中心射流还常出现振颤流动，因此出口总压降低。可见，无激励的附壁保持是需要消耗射流动能即总压为代价的。

无论何种形式的自激励振荡，除了自激励流总压偏低消耗主射流动能外，都不能提供持续的激励(占空比更小)，附壁的多数时间靠康恩达效应维持。需要位差S即振荡腔喷嘴出口宽出较多，以维持稳定附壁。旋涡强度与附壁偏角保持动态平衡，涡流和边界层损失很大。

外激励流后续总压的维持从技术上可轻易实现，且因激励流能量几乎无损地添加进振荡射流，故不需为节省而提前关闭。由于不大需要旋涡低压来维持附壁，可选用更小的位差S以进一步降低涡流损失。

2.4 激励压力缓升降时变模态对振荡性能的影响

2.4.1 数值模拟结果

以上研究激励流的时变特性都是接近矩形的梯形函数，但实际由于调制阀开关特性和激励流管路长度影响，激励流峰值前沿和后沿都会有或多或少的渐升和渐落。研究较为极端的情况，每股激励流的时变特性都为半周正弦曲线

(2)

数值模拟3种不同峰值Ph的半正弦波和近似矩形波激励，其出口总压保持率K的对比如图9所示。图10分别是二者激励流总压PA和对应的出口总压Po时变波形的对比。

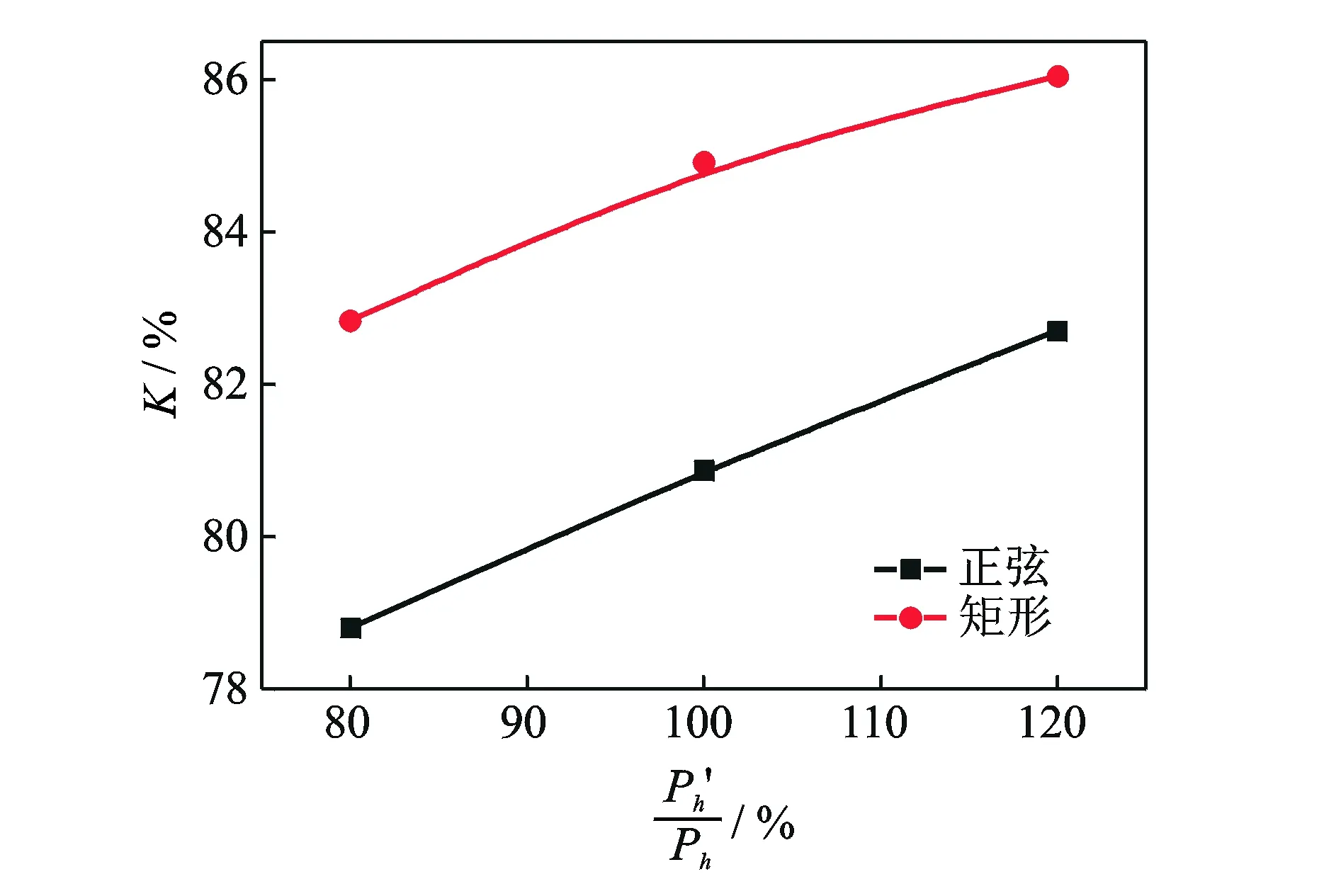
图9 正弦波和近似矩形波激励的总压保持率K对比Fig.9 Comparison of both K of sine and approximate rectangular wave excitation

图10 正弦波和近似矩形波激励的总压时变波形对比Fig.10 Time-varying waveforms of sine and approximate rectangular wave excitation

由图9可知，正弦波激励的总压保持率K也与峰值压力成正比，但比相同峰值压力的近似矩形波，总压保持率K普遍降低约4%。由图10(b)看出，正弦波前沿渐升并未使出口总压Po降低多少，只是使切换附壁略微滞后，而后沿的渐降却使总压按其比例下降，与前面所讨论的随激励流总压峰值升降的响应关系一致。最后阶段，有一小段类似无激励附壁的状态。由于正弦激励流的起始压力很低，故附壁切换也略延迟，但由于主射流早已处于几乎无激励的临界脱壁状态，故压力升至一定值即能切换。

从以上可以看出，激励流前沿渐升的影响较小，而后沿的跌落或提前关闭，总压保持率K将降低4%～6%。选择激励流前半段为正弦、后半段为近似矩形模拟考察，得到的K值仅比全矩形波激励低0.5%～1%。因此，维持激励流后沿总压的持续，是对激励流调制的基本要求。

2.4.2 实验测试结果

实验分别向往复激振器提供矩形波和正弦波两种电源驱动，测得激励口的激励压力波形如图11(a)所示，可见矩形波电源驱动获得的激励流压力峰值较高，谷底压力低，表明切换阀芯在止点的开、闭状况好于正弦波激励。但由于激振器电感电流只能逐增，和输流管道的气容缓冲，激励流前沿跃升无法瞬间完成。对于正弦电源驱动，所获激励流前、后沿更加缓变，但也无法获得标准的正弦曲线，且阀芯到止点后驱动力渐衰，不能维持全开全闭，使波峰压力稍低，波谷压力因泄漏而居高。

两种驱动所对应的振荡器出口压力实测波形如图11(b)所示。可看出其前沿并没有像模拟曲线那样陡峭上升，部分原因是往复阀芯的切换难免两股激励流时间重叠，加之开启瞬时的管路缓冲，导致起始激励压差太小，主射流切换慢，还要同时卷吸一侧渐入和另一侧渐失的低压激励流，多量消耗主射流动能所致。

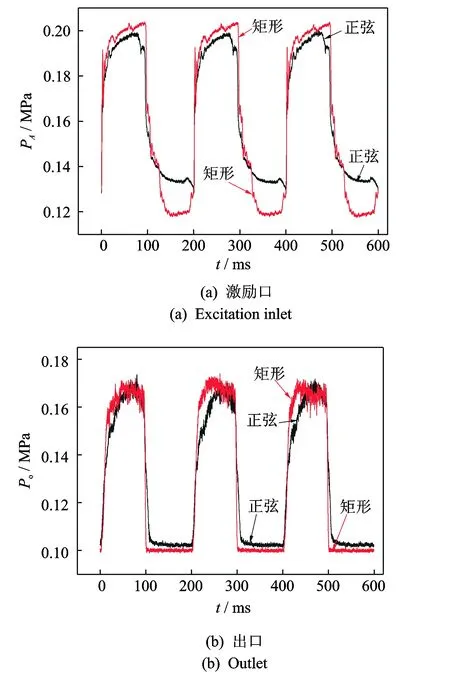
图11 正弦和矩形波电源驱动的实测波形对比Fig.11 Measure waveforms of sine and rectangular wave power driving

上述两种激励流所对应的出口相对总压保持率K1如图12(a)所示。频率低于60 Hz范围，正弦波电源驱动换向阀芯获得激励流，激励振荡的相对总压保持率K1要比近似矩形波的低1%～2%。

2.5 振荡频率对振荡性能的影响

保持其他条件不变，只改变激励频率f(即振荡频率)，实测和模拟出口总压保持率K1(K)随频率变化的关系分别如图12(a)和图12(b)所示。

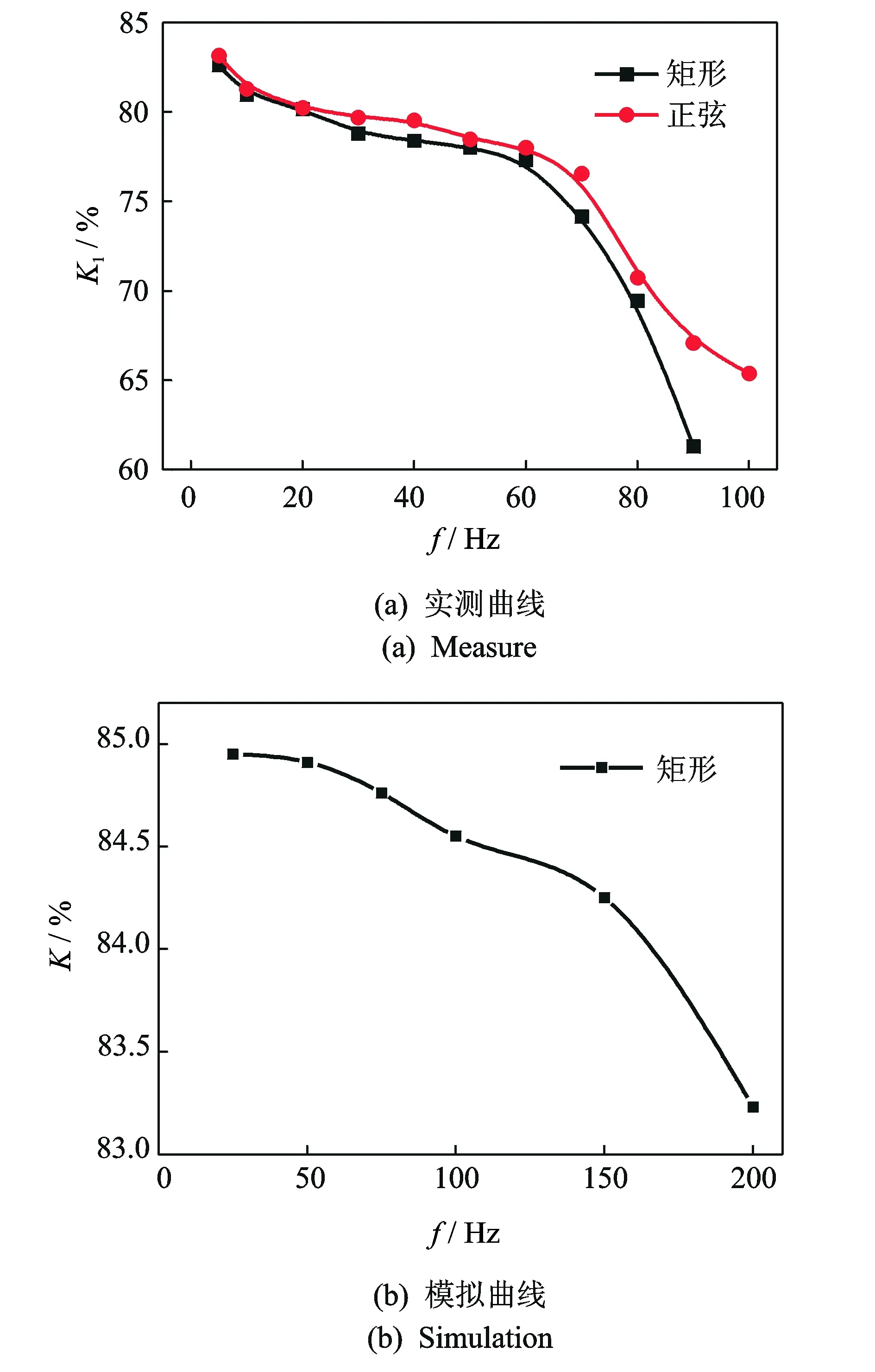
图12 总压保持率随振荡频率的变化Fig.12 Change of retention ratio of total pressure accompanied by oscillation frequency

由于切换过渡期间射流的边界层分离、撞分流劈和激励流起始对同侧弯曲主射流的逆冲角等因素，导致切换期间的总压损失远大于持续附壁阶段。随振荡频率的升高，过渡时间比例增加，总压保持率必然降低。实验K1值在70 Hz前的变化规律，类似于模拟150 Hz前的结果，分别逐降2%和1%左右，但之后均加速跌落。实验考察发现，频率较高时，尽管输入到激振器的功率很大，但其振幅却显著减小(加速度和驱动力与频率平方成正比，故同功率下位移量也按平方速减)，致使往复阀芯不能到达关闭止点，主射流同时卷吸挟带一侧渐入和另一侧泄漏激励流，损失大增，导致实验K1值加速跌落时所对应的频率，只有模拟值的1/2左右。

3 结论

1) 总压保持率K随外激励流总压峰值而变，峰压高于主射流总压20%，K提高1.5%～2%；低于主射流20%，K降低2%左右。

2) 非激励侧激励流的泄漏，使总压保持率降低1%以内，但使激励压差降低，减弱激振能力。

3) 激励流占空比的减小即提前关断，会显著降低总压保持率K，附壁期间只前半时激励，比之全时激励，总压保持率降低近6%。

4) 激励流压力渐升渐降，会降低总压保持率。正弦变化的激励流激励比近似矩形的要低4%左右。渐升的影响较小，渐降影响要大的多。前半段正弦、后半段矩形变化的激励流，K仅比矩形的低0.5%～1%。

5) 总压保持率K随振荡频率f的增加而降低，实验K1值在70 Hz前的变化，与模拟值150 Hz前相似，前者逐步降低了2%，后者降低1%左右。

6) 外激励振荡器对激励流参数的变化具有较强的适应性，20%以内的变化不影响稳定振荡，仍能维持较高的总压保持率。在可振荡范围内，最低的总压保持率K也能比自激励振荡器高出10%以上。

[1] 高传昌,陈豪,雷霆.自激振荡脉冲射流的研究与进展[J]. 华北水利水电学院学报, 2008,20(3):41-44.

Gao Chuanchang, Chen Hao, Lei Ting. Research on self-excited oscillation pulse jet[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power, 2008,20(3):41-44.(in Chinese)

[2] 白亚磊, 明晓. 射流质量流量计的研究[J]. 仪器仪表学报, 2008,29(4):125-128.

Bai Yalei, Ming Xiao. Numerical simulation research of the fluidic mass flowter[J]. Chinese Journal of Scientific Instrument, 2008,29(4):125-128. (in Chinese)

[3] 陈圣涛. 静止式气波制冷机振荡与制冷特性的研究[D]. 大连：大连理工大学, 2008.

[4] Cerretelli C, Kirtley K. Boundary layer separation control with fluidic oscillators[J]. Journal of Turbomachinery, 2009,131(4):041001-041009.

[5] Skarolek V J, Karabelas S. Energy efficient active control of the flow past an aircraft wing: RANS and LES evaluation[J]. Applied Mathematical Modelling, 2016,40(2):700-725.

[6] 程永卓,李宇红,霍福鹏,等. 振荡射流控制翼型流动分离的数值模拟[J]. 清华大学学报:自然科学版, 2002,42(12):1644-1646,1666.

Cheng Yongzhuo, Li Yuhong, Huo Fupeng,et al. Numerical simulation of oscillating excitation separation flow control over airfoils[J]. Journal of Tsinghua University :Science & Technology, 2002,42(12):1644-1646, 1666. (in Chinese)

[7] 王娟. 微射流外激励射流振荡器性能分析[D].大连：大连理工大学，2014.

[8] Li Y, Someya S, Koso T,et al.Characterization of periodic flow structure in a small-scale feedback fluidic oscillator under low-reynolds-number water flow[J].Flow Measurement and Instrumentation,2013,33:179-187.

[9] Cheng Jiao, Zou Jiupeng, Xu Weihua, et al. Research of the characteristics and superiority of external stimulation oscillation jet[C]∥Proceedings of the 2015 4th International Conference on Sustainable Energy and Environmental Engineering. Guangzhou:[s.n.], 2016:611-614.

[10] Zou Jiupeng, Wang Juan, Dai Yuqiang, et al. Study on influence factors of energy hold of outside stimulating jet oscillation[C]∥The Heat Transfer Symposium. Beijing:[s.n.], 2014.

[11] 邹久朋, 胡大鹏, 代玉强, 等. 推挽外激励式射流振荡发生器：中国，ZL201410087495.6[P]. 2016-02-24.

[12] 周光炯,严总毅,许世雄,等. 流体力学[M]. 北京:高等教育出版社, 2000:301-368.

[13] Deconinck H,Roe P L, Struijs R. A multidimensional generalization of Roe′s flux difference splitter for the euler equations[J]. Computers & Fluids,1993,22 (2/3):215-222.

10.16450/j.cnki.issn.1004-6801.2017.06.020

国家自然科学基金资助项目(51276026))

2016-09-12；

2016-10-12

TH48