开口状态及干扰对柱面结构风荷载的影响

孙高健， 马文勇,2， 刘庆宽,2， 刘小兵,2

(1.石家庄铁道大学土木工程学院 石家庄，050043)(2.石家庄铁道大学大型结构健康诊断与控制研究所 石家庄，050043)

开口状态及干扰对柱面结构风荷载的影响

孙高健1， 马文勇1,2， 刘庆宽1,2， 刘小兵1,2

(1.石家庄铁道大学土木工程学院 石家庄，050043)(2.石家庄铁道大学大型结构健康诊断与控制研究所 石家庄，050043)

为满足储煤量、工艺及环保的要求，柱面煤棚结构常常成对出现且在端部和两侧采用不同形式的开口，煤棚间的相互干扰和开口状态对风荷载的影响效应目前尚不明确。针对此问题，通过刚性模型测压试验，研究了端部、两侧开口状态以及煤棚间距对其结构表面风荷载的影响，通过对比结构整体力系数、体型系数分布及脉动风压系数，给出了风向角、开口状态及间距对风荷载的影响规律，分析了其产生机理，并给出了该类结构的风荷载建议。结果表明：半封闭的端部开口方式能有效减小结构整体风荷载，且脉动风压值最小；两侧30% 开孔率的开口形式，结构表面的风荷载分布更均匀，减小结构的脉动风压；煤棚之间的干扰对平均风荷载主要为遮挡效应，对脉动风荷载影响不显著。

风工程； 风压分布； 风洞试验； 三心圆柱面网壳结构； 开口状态； 干扰效应

引 言

三心圆柱面网壳结构是一种广泛应用于储煤结构中的大跨度空间结构，其跨度常达100 m以上，最大可达180 m。这类结构常常需要在端部设置交通通道或者在两侧开口以满足工艺和环保要求，这些开口变化对结构表面的风荷载影响很大。另外，由于存储量大，常常采用多个煤棚近距离布置的结构形式，煤棚之间的相互干扰也对其表面风荷载的估算带来了更多的不确定性。上述问题是目前柱体储煤结构在抗风设计中遇到的急需解决的问题。

已有研究表明，两端封闭状况不仅可以影响结构承受的总体风吸力，也可以改善结构表面的风荷载分布[1-2]。在各种两端开口的方式中，两端半封闭[3]的储煤结构的风荷载取值研究较少。另外，为解决环境保护和交通通行之间的矛盾，具有一定透风率的防风网也开始被用在结构两侧，这种两侧防风网对结构风荷载的影响也不明确。风向角对风荷载也有很大的影响，研究表明最大的风荷载往往出现在斜风向下[4-5]，而目前我国《建筑结构荷载规范》并未提供斜风向下的风荷载取值。对于成对出现的煤棚结构，干扰效应也是其风荷载取值需要关注的重要因素。这种干扰效应从整体风荷载分析，常常表现为遮挡效应，能够减小结构表面的风荷载[6-7]，但是，受扰结构对不同区域影响并不相同[8]。目前，对圆柱面网壳以及其他大跨度曲面网壳结构[9-11]的风荷载分布进行了研究，而该类结构由于其开口状态的复杂性，仍需进一步研究其风荷载分布规律。

通过风洞试验，研究了三心圆柱面煤棚结构端部开口状态、两侧开口状态以及两煤棚的相互干扰对结构表面风荷载的影响，通过对比作用在结构上的整体风荷载给出了结构的最不利风向角、开口及干扰状态，并进一步通过风荷载分布解释了其形成的原因。结果不仅可以为该类结构的初期选型提供建议，也可以为类似结构的抗风设计提供风荷载取值依据。

1 试验介绍

1.1 模型概况

笔者针对长为220 m、宽为120 m、高为54.2 m、矢跨比为0.45的三心圆柱面网壳结构进行研究，该网壳面由中心一段半径r=66.6 m、圆心角φ=70°圆弧和两端半径r=45.3 m、圆心角φ=46°的圆弧组成，底部支撑高度为6 m。Ln为网壳结构纵向测点行标号，Ln=1～11；α为横向测点位置参数，α=0°～180°。试验模型采用有机玻璃板制成，具有足够的强度和刚度，模型缩尺比为1∶200，每个测压孔布置1对测点，内外同步测压，测点布置沿模型纵向划分为11个剖面，每个剖面在全拱方向上布置18个测点。试验模型概况见图1，x轴、y轴及z轴正向如图1所示，坐标系满足右手定则。

图 1 试验模型概况Fig.1 Model diagram

1.2 试验简介

试验在石家庄铁道大学风洞试验室进行，试验段宽为4.4 m，高为3 m，长为24 m。用粗糙元和尖劈模拟实际工程所在A类地貌，图2为A类地貌平均风剖面、紊流度剖面[2]。试验自由来流风速为11 m/s，数据采集系统采用DTC Initium型电子式压力扫描，采样频率为330 Hz，采样时间为30 s，采样点数为9 900点。试验相似比见表1。

图 2 平均风剖面和紊流度剖面Fig.2 Mean velocity profile and turbulence intensity profile

名称模型值原型值相似比长度比110cm×60cm220m×120m1∶200风速比11m/s24m/s1∶2时间比33s55min1∶100

1.3 试验工况

试验来流垂直于模型纵轴方向为0° 风向角，风向角β按顺时针方向增加，以10°为间隔，在0° ～ 180° 风向角下进行试验(见图1)。两端开口状态分为两端开口、两端半封闭、两端全封闭3种情况，其中两端半封闭底部距地面高度为8 m，3种开口情形见图3。沿结构长度方向，在立柱侧面有2种开口状态，定义开孔率为δ，δ=0时为两侧全封闭状态，δ= 30% 时为两侧30%开孔率状态。两侧开口状态见图4。由于固定模型的需要，煤棚模型支座底部沿长度方向设置2 cm宽的ABS板制成的长条，干扰间距指两煤棚支撑底部长条间的距离。干扰间距用I表示，取I= 0,20,40,60,80,100和120 cm共7个间距进行试验，其中模型跨度距离D=60 cm，则I/D分别为0，0.3，0.7，1，1.3，1.7和2。

图 3 3种开口状态Fig.3 Three open states

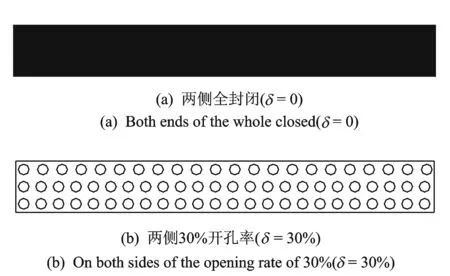
图 4 两侧开口状态Fig.4 Open state on both sides

1.4 参数定义

采用无量纲风压系数描述结构表面风压

(1)

其中：Cpi为i点的风压系数，pi为测点i处的压力；ps为参考点静压；pt为参考点总压；ρ为空气密度；Ur为参考点风速。

定义净压系数为

Cpdi=Cpwi-Cpni

(2)

其中：Cpdi为i测点位置的净压系数；Cpwi和Cpni为i测点位置对应的外表面测点和内表面测点的风压系数。

下面用Cpdimean和Cpdirms表示Cpdi的净压系数均值和净压系数均方根值，净压体型系数可由净压系数均值求得

(3)

其中：μsdi为测点i的净压体型系数；Zi为测点i所处的高度；α为地面粗糙度指数，本试验为A类地貌，α= 0.12。

净压脉动风压系数可由净压系数求得

(4)

其中：Cpdirms为净脉动风压系数；Cpdimean为净风压系数均值；N为每个样本采样点的数目，本试验中N=9 900。

将作用在结构上的风压在各风向角下进行积分，得到结构的整体力系数，此处的整体力系数指结构受到的平均力，定义y，z方向及y与z合力方向的无量纲整体力系数分别为Cy，Cz，Cc

其中：Cpdi为i测点位置的净风压系数；Ai为测点i所属面积；θi为测点法线方向与水平方向的夹角(θi≤ 90°)；D为模型的宽；L为模型的长；H为模型的矢高。

对式(5)～式(7)说明如下：将作用在结构上的平均风压沿y，z两个方向进行分解，然后进行无量纲化即得到y，z方向整体力系数Cy和Cz，将这两个方向的力系数合成，即得到合力方向的整体力系数Cc。

2 开口状态的影响

2.1 力系数分析

图5给出了端部3种开口状态与两侧2种开口状态下结构的力系数随风向角的变化规律。

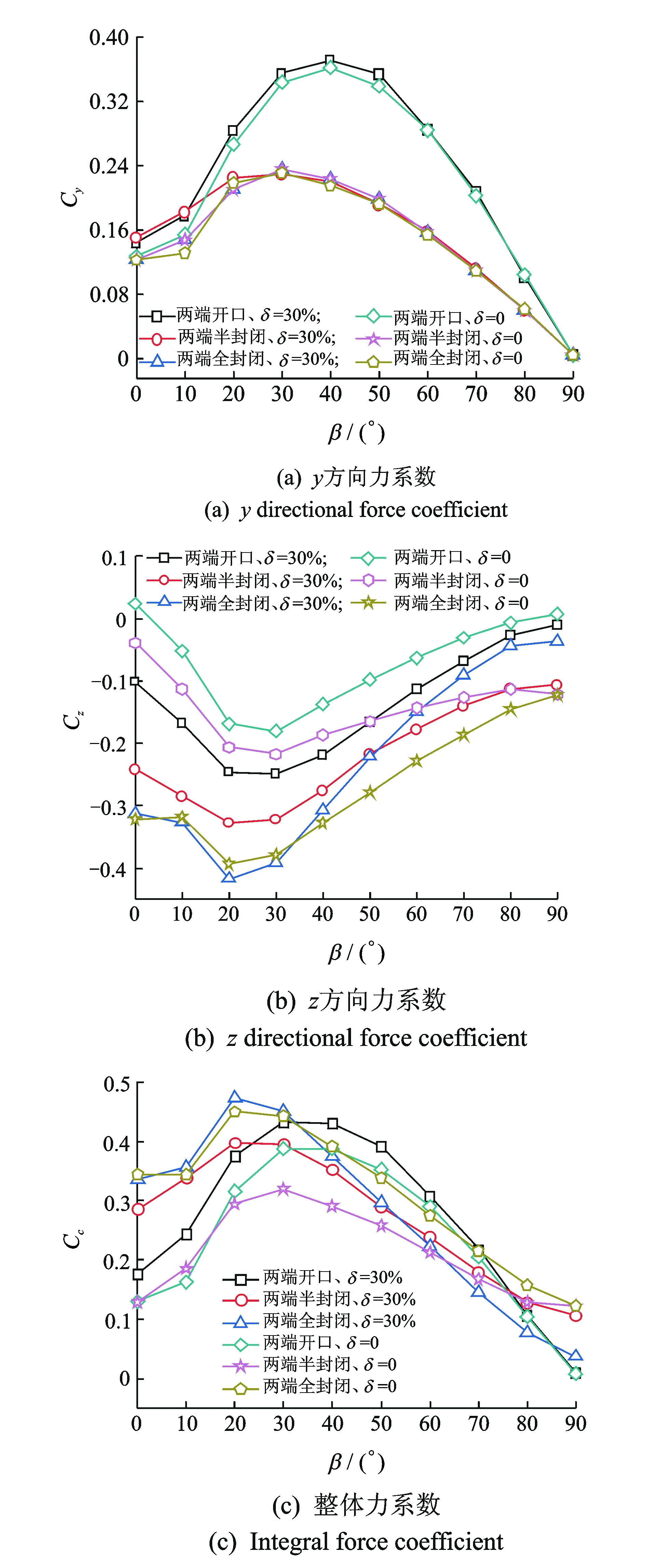
图 5 力系数随风向角变化规律Fig.5 Variation of force coefficients with angle of attack

由图5可知，不同开口状态下力系数的变化趋势一致，随风向角的增加而先增大然后减小，30°～40° 风向角附近力系数最大。从图5(a)可以看出，0° ～ 90° 风向角内，端部为开口状态时Cy最大，两端全封闭与两端半封闭Cy相同，两端开口水平推力最大，两侧开口状态对水平推力几乎没有影响。由图5(b)可知，受开口状态的影响，Cz呈现明显的梯度变化，两端全封闭结构受到的风吸力最大，两端全封闭情况下，两侧30% 开孔率能够减小结构受到的风吸力。由图5(c)可知，从整体平均力角度考虑， 结构在30°～ 40° 风向角附近最为不利，在最不利风向角下两端半封闭、两侧全封闭Cc值最小。

2.2 体型系数分析

以整体力最大的30° 风向角为例，图6给出了不同开口状态下体型系数的分布。

图6 体型系数分布Fig.6 Pressure coefficients distribution

由图6可知，结构迎风面体型系数为正值，随着高度增加呈现出明显的梯度变化，由结构底部到中部数值逐渐减小，结构顶部形成最强负压区域，由结构顶部至结构背风区域，负压逐渐减弱。

对图6体型系数等值线图进行对比，可以看出图中所示Ⅰ,Ⅱ区域出现强负压区域，其出现使得结构表面风压分布变得更不均匀。由于端部开口，斜风向(β=30°)下风直接吹向结构区域Ⅰ内表面，内压为正压，该正压增强了结构表面的净负压，使得y方向受力较大。两端全封闭阻挡来流穿过结构内部，来流在结构顶部分离速度较快，在区域Ⅱ形成较大的负压区，同时增加了结构整体的风吸力。从图中可以看出，两端半封闭的开口状态由于两端遮挡，结构y方向的风压受到减弱，同时来流在顶部的分离速度减缓，z方向的风压减小，使得结构表面风压分布更均匀。

2.3 脉动风压系数分析

以整体力最大的30° 风向角为例，图7给出了不同位置处结构脉动风压系数的分布。

图 7 脉动风压系数分布Fig.7 Fluctuating wind pressure coefficients distribution

由图7(a)可以看出，在结构端部位置(Ln=1)，α=0°～180°范围内，两端开口状态下，两侧全封闭与两侧30%开孔率的脉动风压系数重合，α从0°～90°范围变化时，两端半封闭(两侧全封闭、两侧30%开孔率)与两端全封闭(两侧全封闭、两侧30%开孔率)脉动风压系数基本重合，α在90°～180°范围内变化时，上述4种工况下的脉动风压系数大小略有差异。可以得出，两侧的开口状态对脉动风压系数没有影响，而两端开口状态对脉动风压系数略有影响，两端开口情况下，结构表面脉动风压系数值最大。

由图7(b)可知，Ln=3截面处，脉动风压系数的分布受开口状态影响明显，α=20°左右时不同开口状态下结构的脉动风压系数均达到最大值，其中，两端开口时结构的脉动风压系数约为0.6。α=0°～180°范围时，两端开口、两侧全封闭时结构的脉动风压系数值最大，两端半封闭、两侧30%开孔率脉动风压系数值最小。位于40°<α<180°范围内的测点，不同开孔状态结构脉动风压系数变化不显著，两端开口(两侧全封闭、两侧30%开孔率)情况下脉动风压系数在0.2附近波动，而两端半封闭(两侧全封闭、两侧30%开孔率)与两端全封闭(两侧全封闭、两侧30%开孔率)脉动值在0.1附近变化。

从图7(c)可以看出，结构中间位置处(Ln=6)脉动值变化较为剧烈，6种不同开口状态工况下脉动值之间略有差异。从脉动风压分布的总体趋势可以看出，两端开口、两侧全封闭状态脉动值最大，两端半封闭、两侧30%开孔率下脉动值最小。

3 干扰效应的影响

3.1 力系数分析

以两端半封闭、两侧30%开孔率的开口状态为例，研究干扰效应对风荷载的影响。图8给出了施扰结构位于受扰结构上游时力系数分布图。

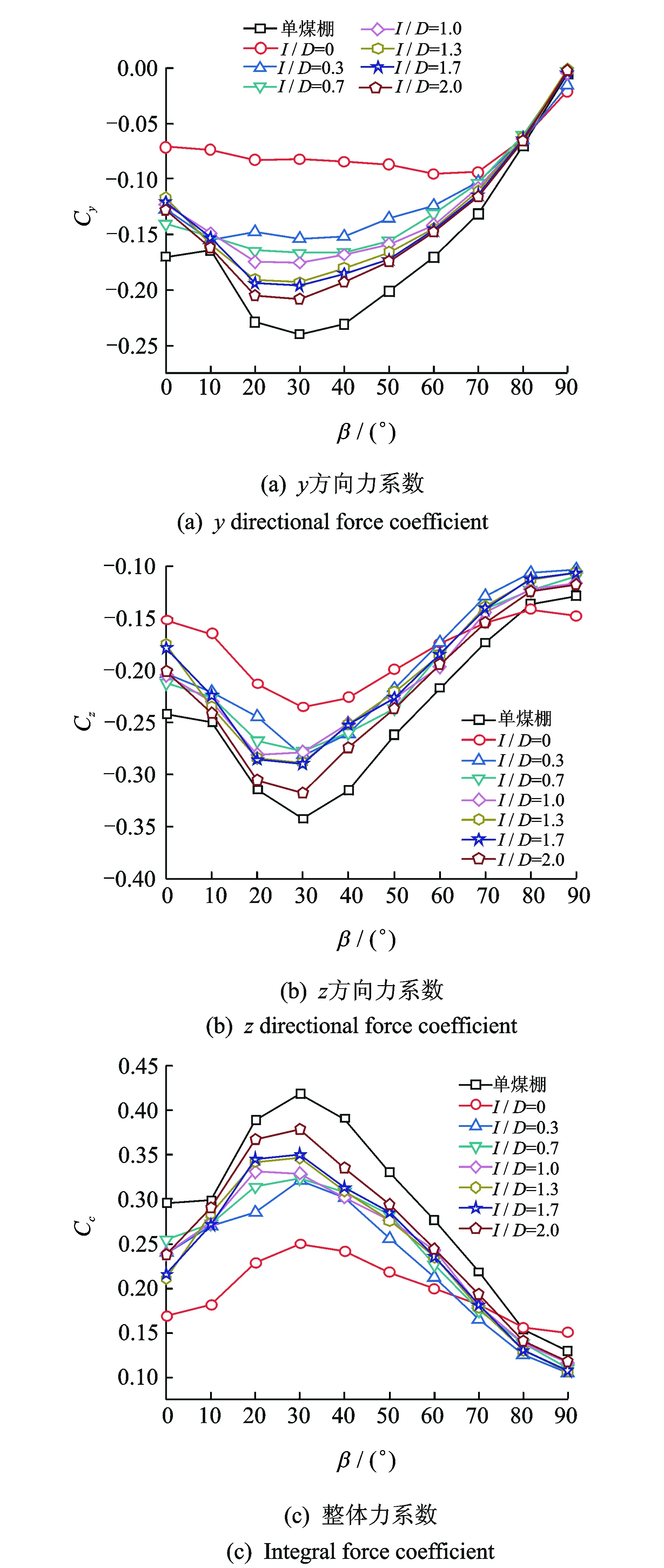
图 8 下游结构力系数随风向角变化规律Fig.8 Variation of force coefficients on the leeward structure with angle of attack

当施扰结构位于受扰结构上游时，由于其遮挡效应使得结构力系数减小，其中0倍间距下遮挡效应最为明显。随着干扰距离的增加，遮挡效应逐渐减弱，从结构受力角度考虑，30°风向角仍为结构受力最不利工况。由图8(a)可知，由于施扰结构与受扰结构紧邻，β= 0°～ 70°之间，受扰结构完全位于施扰结构尾流区，I/D=0时，Cy值随风向角变化不大，其值约在-0.09 ～ -0.07左右。80° ～ 90° 风向角附近，施扰结构的遮挡效应减弱，使得无干扰与多种间距干扰下的Cy值相当，遮挡效应对水平推力影响较大。从图8(b)可知，风吸力的大小也受到遮挡效应的影响，施扰结构距离受扰结构越近，遮挡效应越强，风吸力减小，反之遮挡效应越弱，风吸力增大。由图8(c)可知，干扰效应有利于减小结构的整体平均力，整体平均力的大小受干扰距离影响显著。

图9给出了施扰结构位于受扰结构下游时的力系数分布图。从图9可以看出，当施扰结构位于下游时，仍然会对上游结构的风荷载产生影响。从整体力系数上来看，在受力最强的30°风向角左右，下游施扰结构使得上游受扰结构的风荷载减小，这说明下游施扰结构可以降低上游受扰结构的风荷载。虽然在某些风向角下(如90°)，下游施扰结构会增强上游受扰结构的风荷载，但是从最不利风荷载取值上来看，位于下游的施扰结构对降低上游的受扰结构的风荷载值是有利的。

图 9 上游结构力系数随风向角变化规律Fig.9 Variation of force coefficients on the windward structure with angle of attack

3.2 体型系数分析

当施扰结构位于受扰结构下游时，以30° 风向角为例对受扰结构体型系数进行分析，图10给出了30° 风向角下结构中间列体型系数的分布。虚线表示无干扰煤棚体型系数值，实线表示受扰后煤棚体型系数值。

图 10 体型系数分布Fig.10 Pressures coefficients distribution

由图10可得，由于干扰效应的影响，与无干扰相比体型系数有所减小。其中：水平推力的减小主要是由于迎风向正压的减小，背风向的体型系数变化不大；竖向力的减小主要体现在顶部负压的减弱。各种间距下体型系数的分布规律并没有发生明显变化，其值也变化不大，因此在实际应用中，间距大小对体型系数分布的影响可以忽略。

3.3 脉动风压系数分析

图11 脉动风压系数分布Fig.11 Fluctuating wind pressure coefficients distribution

图11给出了中间列测点的脉动风压系数分布。由图11可得，脉动风压系数的分布受干扰效应的影响，干扰间距为1.3倍跨距可以看作干扰效应的分界线。1.3倍跨距之前的干扰对于结构左跨脉动风压系数有放大作用，对右跨脉动风压系数基本没有影响；1.3倍跨距之后的干扰使得结构整跨的脉动值与无干扰时重合，可知1.3倍跨距后干扰对脉动风压系数的分布没有影响。

4 抗风设计建议

为便于设计人员使用，笔者将干煤棚表面划分为9区域，如图12所示，表面9区域体型系数取值见表2。表2中给出的体型系数并非为0° 风向角下的取值，而是根据力系数判断的最不利风向角下对应的体型系数值。

图12 分为9块的煤棚Fig.12 Divided into nine blocks of coal shed

区域两端全封闭两端半封闭两端开口δ=30%δ=0δ=30%δ=0δ=30%δ=010．60．70．30．50．10．220．30．50．10．3-0．1030．20．400．2-0．104-0．7-0．6-0．7-0．5-0．9-0．95-0．8-0．6-1．0-0．8-1．1-1．16-0．5-0．4-0．6-0．4-0．8-0．77-1．1-1．0-0．6-0．4-0．6-0．78-0．3-0．1-0．4-0．2-0．5-0．59-0．10-0．3-0．1-0．4-0．3

建议煤棚设计选用两端半封闭、两侧30% 开孔率的形式，干扰效应对结构抗风是有利的，在设计时对干扰效应可不予考虑。

5 结束语

以某三心圆柱面网壳结构为背景，研究了开口状态及干扰效应对结构风荷载的影响。通过对结构整体力系数的分析，发现结构在30° 风向角附近平均风荷载最大，与文献[3-4]中此类结构30° ～ 45° 为最不利风向角结论一致。对3种不同开口状态的力系数进行比较，建议采用两端半封闭开口方式，这种方式不仅可以有效地减小整体风荷载，使得风荷载在结构表面分布更均匀，而且结构受到的脉动风压最小。两侧全封闭与两侧30%开孔率均可以减小结构整体风荷载，且减小的幅度相当，而两侧30% 开孔率结构承受的风压脉动值更小，且利于煤棚内部通风，符合环保要求，应优先选用。多种不同间距下的干扰试验，无论是施扰结构位于受扰结构的上游还是下游，都会减小受扰结构的最大平均风荷载。从平均风荷载的角度看，干扰主要表现为遮挡效应，对结构抗风设计是有利的，从脉动风荷载考虑，1.3倍跨距之后不需考虑干扰的影响。

[1] 马文勇, 刘庆宽, 肖彬. 典型拱形壳体风荷载分布规律[J]. 土木建筑与环境工程, 2011, 33(5): 63-68.

Ma Wenyong, Liu Qingkuan, Xiao Bin. Wind loads distribution on typical vaulted shells [J]. Journal of Civil, Architectural & Environmental Engineering, 2011, 33(5): 63-68. (in Chinese)

[2] 马文勇, 刘庆宽, 肖彬, 等. 三心圆柱面网壳结构风荷载分布规律[J]. 工程力学, 2011, 28(S2): 166-170,209.

Ma Wenyong, Liu Qingkuan, Xiao Bin, et al. Wind pressure distribution on three centered cylindrical latticed shell [J]. Engineering Mechanics, 2011, 28(S2): 166-170,209. (in Chinese)

[3] 罗尧治,张浩.弦弓式预应力柱面网壳结构风洞试验及风致效应研究[J].空间结构，2005(2):3-8,26.

Luo Yaozhi, Zhang Hao. Wind tunnel fest and wind-induced response of string-bao prestressed cylindrical latticed shell[J]. Spatial Structures,2005(2):3-8,26. (in Chinese)

[4] 齐月芹, 李皓玉. 大跨度干煤棚网壳结构风荷载试验研究[J]. 空间结构, 2010, 16(4): 55-59.

Qi Yueqin，Li Haoyu. Experimental investigation of wind load on large-spandry-coal-shed latticed shell [J].Spatial Structure, 2010, 16(4): 55-59. (in Chinese)

[5] 黄鹏, 顾明, 叶孟洋. 干煤棚柱面网壳结构风荷载试验研究[J]. 建筑结构, 2011, 41(S1): 1432-1437.

Huang Peng, Gu Ming, Ye Mengyang. Experimental study on wind loads on cylindrical reticulated shells [J]. Building Structure, 2011, 41(S1): 1432-1437. (in Chinese)

[6] 黄鹏, 兰志昆, 顾明. 干煤棚柱面网壳结构多参数风荷载试验研究[J]. 建筑结构, 2015, 45(17): 92-98,62.

Huang Peng, Lan Zhikun, Gu Ming. Experimental study of dry coal shed parameters of wind load on cylindrical reticulated shell structure [J]. Building Structure, 2015, 45(17): 92-98,62. (in Chinese)

[7] 周晅毅, 顾明, 米福生, 等. 干扰条件下煤棚结构风致干扰特性研究[J]. 振动工程学报, 2009, 22(6): 652-658.

Zhou Xuanyi, Gu Ming, Mi Fusheng, et al. Interference effects on wind-induced responses of dry coal sheds [J]. Journal of Vibration Engineering, 2009, 22(6): 652-658. (in Chinese)

[8] 刘庆宽, 卢照亮, 郑云飞, 等. 大跨球壳结构风压分布规律和风致干扰效应试验研究[J]. 建筑结构学报, 2016，37(10): 140-146.

Liu Qingkuan, Lu Zhaoliang, Zheng Yunfei, et al. Experimental study on shell structure of the wind pressure distribution and wind-induced interference effect of long-span ball [J]. Journal of Building Structures, 2016, 37(10): 140-146. (in Chinese)

[9] Li Yuanqi, Tamura Y, Yoshida A. Wind loading and its effects on single-layer reticulated cylindrical shells [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2006, 94(12): 949-973.

[10] Cheng C M, Fu C L. Characteristic of wind loads on a hemispherical dome in smooth flow and turbulent boundary layer flow [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(6/7): 328-344.

[11] Faghih A K, Bahadori M N. Three dimensional numerical investigation of air flow over domed roofs [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(3): 161-168.

10.16450/j.cnki.issn.1004-6801.2017.06.006

河北省自然科学基金青年资助项目(E2013210132)；河北省教育厅优秀青年基金资助项目(YQ2014039)

2016-11-11；

2017-01-09

TU312+.1； TH126

孙高健，男，1991年9月生，硕士生。主要研究方向为结构振动与控制。曾发表《太阳能光伏极风荷载分布模型试验研究》(《振动与冲击》2017年第36卷第7期)等论文。

E-mail:15733171487@163.com