基于无先验声速的迭代搜索定位方法∗

于 平 谢 胜

1 引言

水下大范围跟踪定位一般需要在目标上加装合作信标，测量阵元布设成基线几公里的四边形观测几何，对阵内目标进行定位跟踪测量。测量阵元通常利用应答方式或同步方式获得测距信息，至少需要3个阵元的位置信息，以及目标的传播时延测量信息联立球面交汇方程组［1～8］。

迄今国内外几乎所有的水下定位系统，均事先采用水文测量获取平均传播声速，计算与传播时延测量值的乘积，换算成各阵元的测距信息。

常规定位算法或解算模型的弊端在于：1）需要事先通过水文测量，获取平均传播声速的先验值，并装订于定位软件；2）事实上，水中传播声速具有显著的时变、空变特征，各阵元因信道差异而导致声速的非一致性，且发生较快速的数值起伏现象；3）当平均声速装订值出现偏差时，由球面交汇方程组解算的目标位置，致使定位的系统误差和随机误差增大［4～12］。

2 无先验声速迭代搜索方法

2.1 算法模型

在海底或海面布设N个测量阵元，水下目标作定深航行，目标声源在同步信号触发下周期性地发射声信号，各接收阵元接收测量声信号传播时延，建立球面交汇模型［1～8］：

式中，未知量（X，Y，Z）为待测目标的位置坐标；（Xi，Yi，Zi）为阵元i的位置坐标；Ci为阵元i对应的传播声速；τi为目标到阵元i的声传播时延，由水声跟踪定位系统测得。

建立观测矩阵方程：

式中，（X，Y，Z）表示本次迭代计算预测值，（ X0，Y0，Z0）表示初值（前次迭代计算预测值），α为迭代搜索步长。矩阵及向量表示为

2.2 迭代搜索模型

任意选取目标的初值位置（X0，Y0，Z0），按照如下迭代过程进行解算：

1）设置海区可能的声速最小值到最大值范围，各阵元假定任意一组声速搭配，由式（1）建立球面交汇方程组，按照如下2）～4）步骤进行循环搜索迭代求解；

2）由式（2）矩阵方程进行一步预测，得出新的目标位置坐标；

3）根据式（5）计算各阵元测量斜距与预测值斜距的差值并统计均方误差；

4）判断该均方误差是否小于设定门限，未达到门限即将本次预测值作为初值重复以上2）～4）步骤，直至收敛于稳定的均方误差；

5）按照各阵元声速的配对关系，挑选均方误差极小值，对应的预测值即为目标的位置坐标，对应的声速组即为各阵元对应的声速。

2.3 模型分析

充分的试算表明，迭代算法稳健收敛，通常经3～4步即完成收敛运算。值得注意，矩阵方程的迭代步长由经验确定，以确保算法的收敛性和收敛速度。

算法模型的描述基于冗余测量，对方程数约束较宽，因此多个方程参与迭代可抵消测量误差，从而提高定位精度。当有效阵元个数即方程个数与未知量个数相等时，由于没有冗余信息判别真解、假解（双解现象），此时算法将收敛于距离初值位置较近的真解或假解。也就是说，如果没有冗余阵元信息，初值选取不当算法有可能收敛于假解。鉴于这种情况，初值选取的原则是：尽可能根据测量方案的先验知识，将初值限定于目标就位点位置的小范围内，尔后的解算初值只需要替换前一帧的迭代结果即可。

3 无先验声速迭代搜索方法应用效果分析

3.1 海面浮标基阵定位系统海上静态实验精确度评估结果

如图1所示，测量基线约4km，声源深度约6m，浮标DGPS精度约0.6m，目标声源DGPS精度约0.25m，定位系统采用同步测距工作方式［12］。在E1点区域共获得1～3组数据，E2和E3区域分别获得4、5组数据。

表1列出了常规定位模型的系统误差和随机误差，同时给出固定声速迭代算法（取水文测量声速值）和声速搜索迭代算法（声速搜索范围1530m/s～1540m/s）的定位精确度评估结果，最后由搜索声速的平均值再次带入固定声速迭代模型进行解算评估。数据表明，由声速搜索迭代算法平滑求解声速平均值，再带入固定声速迭代算法进行解算，可明显改善阵中区域的精确度。

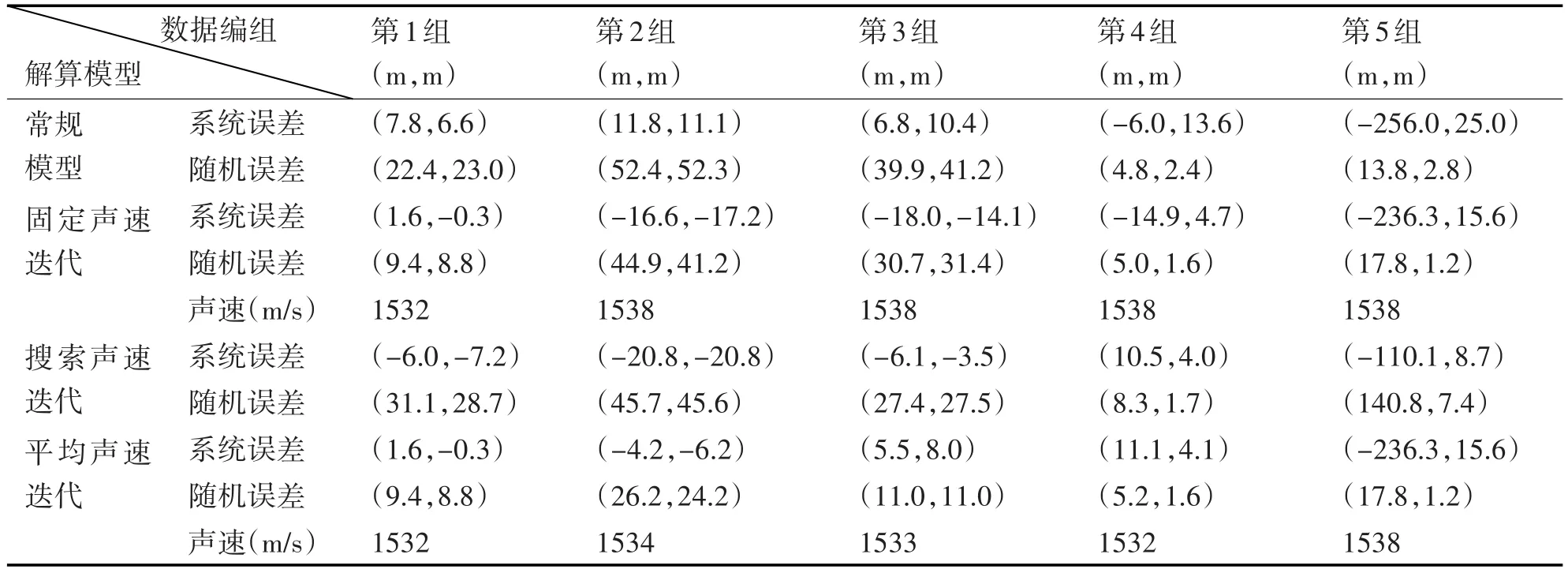
表1 海面浮标基阵定位系统海上静态实验精确度评估结果

3.2 海面浮标基阵定位系统海上动态实验精确度评估结果

在图2中，4枚海面浮标阵元布设成四边阵形，基线约2海里，目标声源深度7m。目标航迹分成了3段典型航路，定位系统采用同步测距工作方式。

表2数据对定位算法精度进行比较，同时给出固定声速迭代算法（取水文测量声速值）和声速搜索迭代算法（声速搜索范围1520m/s～1540m/s）的定位精确度评估结果，分别给出测量精度的统计评估。数据表明，常规解算模型存在着较大的系统偏差和随机误差，尤其当采用固定声速的迭代算法后，阵中区域可明显提高测量精确度。

3.3 海底潜标基阵定位系统海上动态实验精确度评估结果

在图3中，共布设6个海底潜标，分别组成1×2km和2×2km测量阵形，共获得2个航路的实验数据。

表2 海面浮标基阵定位系统海上动态实验精确度评估结果

海区深度约40m，声速分布呈负梯度，询问换能器深度约5m，采用询问应答测距方式。将试验航路分为4段分别给予数据处理，装订平均声速1532m/s进行固定声速迭代解算，统计精确度列于表3。

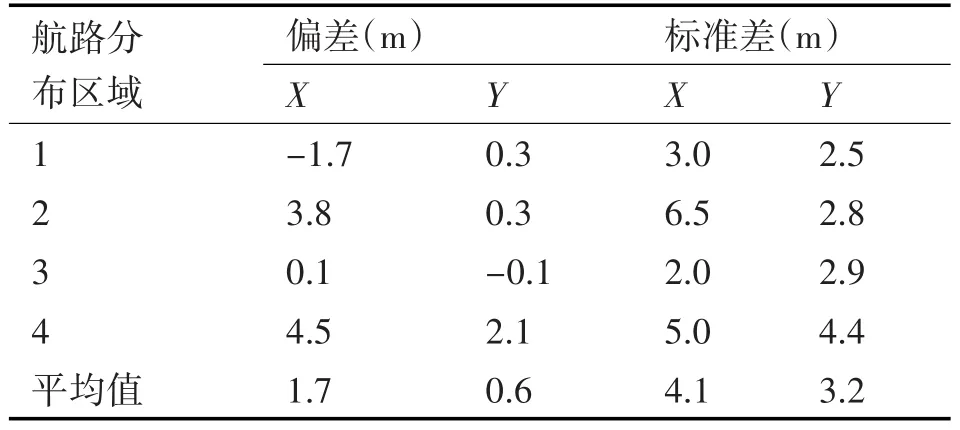
表3 海底潜标基阵定位系统海上动态实验精确度评估结果

结果表明，缩短基线有利于提高定位精度，缘于多路径干扰减弱，但是极限定位精度大约只能达到2m～3m。此外，固定声速的装订对定位标准差影响较大，为提高定位精度，必须在精度评估的基础上慎重考虑声速的装订问题。

4 结语

无先验声速迭代定位算法，实现了对各阵元非一致声速进行折中的平滑处理，而无需装订先验的声速值。尤其利用冗余阵元的预测迭代解算时，多个方程参与迭代可以抵消测量误差，从而提高定位精度，并且能够自动搜索各阵元声速。仿真及海试结果表明，该算法稳健收敛，运算速度快。

［1］田坦.水下定位与导航技术［M］.北京：国防工业出版社，2007：46-65.

［2］李守军，包更生，吴水根.水声定位技术的发展现状与展望［J］.海洋技术，2005，24（1）：130-135.

［3］李嶷，孙长瑜.不同布阵方式下球面交汇定位系统性能分析［J］.声学技术，2008，27（5）：649-653.

［4］吴永亭，周兴华，杨龙.水下声学定位系统及其应用［J］.海洋测绘，2003，23（4）：18-21.

［5］R.J.尤立克.水声原理［M］.洪申译.哈尔滨：哈尔滨船舶工程学院出版社，1990：79-183.

［6］马大猷.现代声学理论基础［M］.北京：科学出版社，2004：5-31.

［7］刘伯胜，雷家煜.水声学原理［M］.哈尔滨：哈尔滨工程大学出版社，2002：59-119.

［8］钱洪宝，孙大军.水声定位系统现状［J］.声学技术，2011，30（3）：389-391.

［9］Lurton X.Swath bathymetry using phase difference：Theoretical analysis of acoustical measurement precision［J］.IEEE Journal of Oceanic Engineering，2000，25（3）：351-363.

［10］杨日杰，王正红等.浮标阵形对搜潜效能影响的研究［J］.计算机仿真，2009，20（12）：16-20.

［11］王泽民，罗建国等.水下高精度立体定位导航系统［J］.声学与电子工程，2005，2：1-3.

［12］于平，吴波.长基线水声定位基阵阵形优化设计.舰船电子工程，2015，35（5）：125-127.