CVD 预测模型精确度优化措施探究
2022-05-05尹帅帅石更强孙旭阳
尹帅帅, 石更强, 孙旭阳
(上海理工大学 健康科学与工程学院,上海 200093)
根据最新统计,全世界每年因心血管疾病(CVD)而死亡的人数约1 530 万人,占总死亡人数的1/4,CVD 已成为全世界高发病率和高死亡率的主要疾病[1-2]。随着大数据技术的发展,CVD 相关诊断数据也在持续增加,为今后疾病诊断和预防提供了很好的数据基础[3-4]。CVD 是由遗传、环境、行为、疲劳等多种因素共同作用导致的[5],风险预测模型可以整合这些因素,利用机器学习(ML)进行疾病预测[6]。风险预测模型的精确度对于疾病风险分层和中危人群重分类具有重大意义,努力提高预测模型精确度,可以及时对高危人群进行追踪、防控和个体化干预,减少疾病带来的危险。
目前国内外关于风险预测模型的研究中,还没有对如何提高CVD 风险预测模型精确度进行系统性的论述。Bouwmeester 等[2]探究近期文献中预测模型如果按照传统方法学建议进行建模,是否会导致较差的预测结果[7-9]。Wessler 等[10]通过对模型进行总结和比较,指出现今预测模型存在的局限性。预测模型的分析不能仅仅局限于对预测结果的探讨,而更应该注重构建模型的各个模块对结果产生的影响。Damen 等[11]探讨了预测模型的危险因素、预测结果、预测性能、外部验证等。Siontis 等[12]收集了大量模型的区分、校准、重分类等信息,对特定信息偏差是否会影响预测模型的结果进行评估。Cooney 等[13]和Cui[14]探讨了单因素和多因素对预测结果的影响。为了更好地改善预测模型的精确度,改善青年、中年、老年同一预测模型、不同预测结果而带来的不同个体化、精确化干预措施,本文检索了大量文献,对比了从数据选择到最后模型评估的整个内容,就如何提高风险预测模型精确度进行综合性探讨。
1 文献检索与探究
1.1 文献处理
文献选择:为了提高研究的价值和意义,手动检索了国内外在医学领域影响力较高的395 篇文献,通过对每篇文献的题目和摘要进行仔细审阅,得到95 篇与研究相关的文章,通过对整篇文章阅读与分析,剔除了非科研论文和建模不完整文献,保留了余下的62 篇文献。
入选原则:文献必须是原创性研究型论文,本研究主要寻求改善预测模型精确度的方法,因此,文献必须包含样本选择与处理、特征值选择、预测模型搭建、预测性能探究、模型风险评估等一项或多项改善措施,文献中必须包含针对某些人群的预测结果。最后对保留的62 篇文献进行交叉性和系统性研究,并根据项目的不同进行文献占比分类。整个流程如图1 所示。
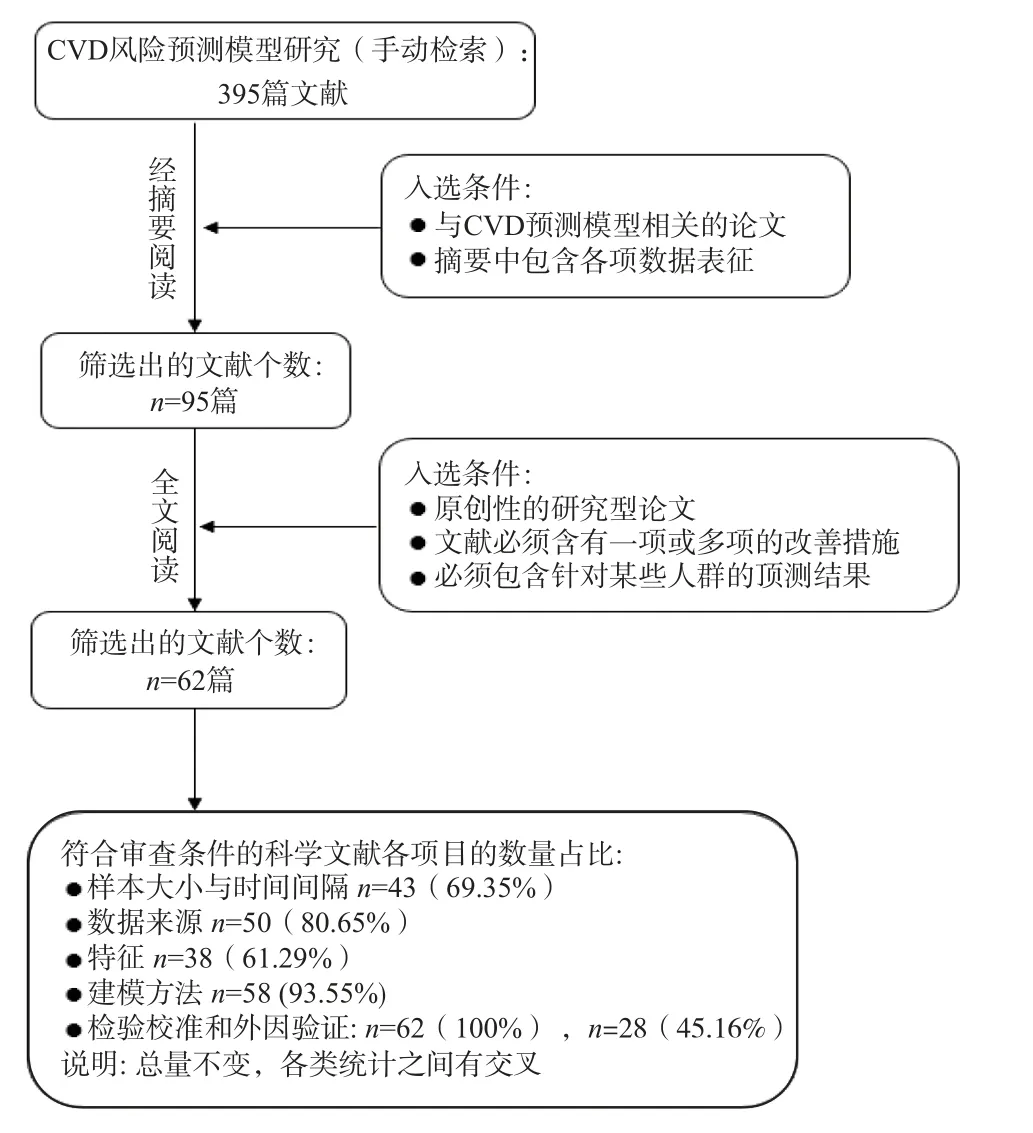
图1 文献入选流程图Fig.1 Flowchart of literature inclusion
1.2 数据处理
制定列表:为了更加方便直观地展示探究结果,本文制定了列表式对比评分机制。涉及项目包含预测目标、模型种类、数据对象等[15-16],极大地提高了数据的可利用性。
数据挖掘:数据挖掘是为了探究各预测模型之间的相同或不同之处,从中找到可以改善的方面。
精确度等级百分率:精确度作为研究的主体,根据探究目的创新地提出精确度等级百分率。每个模块进行分类后,得到的文献数目各不相同,在进行精确度对比时,无法保证单一变量,无法消除文献数目不同对结果的影响。因此,将精确度进行等级划分,将文献各自精确度按等级归类,然后将等级归类后的文献数量进行百分率化得到聚集区,最后进行数据分析与比较,得出所需要的数据意义。
精确度等级百分率的意义在于消除了基数不同带来的对比影响,将不同数据利用最大化,挖掘数据潜在价值,容易得出聚集区、众数、中位数、平均数、最大值、最小值、数值走向和各数据的意义,这是对数据挖掘思想的体现,对本研究至关重要。
1.3 探究内容
一个完整的预测模型一般包括4 大模块[17],为了寻求改善预测模型精确度的措施,本文对这4 个模块进行探究。
a. 样本大小和时间间隔。对各类文献的样本大小、时间间隔、精确度进行数据处理、相关性分析、描述统计分析、横纵向对比,绘制相应的评分表格和散点图,经数据挖掘得出最小样本量和最小时间间隔[18]。
b. 数据来源。探究改进电子健康记录(EHRs)的优势,将不同数据来源进行纵向精确度等量对比,得出最合适的数据来源,并对各数据来源的优缺点和应用范围进行分析[19]。
c. 特征。将改进特征选择方法的各算法进行比较,得出最优的特征选择方法;比较纳入新特征前后的精确度,判断该特征是否改善了精确度;将不同特征选择方法进行纵向比较,判断是否选择更多相关的特征可以提高预测模型精确度。
d. 建模方法。对回归分析进行简单的分类、对比,并对各自的适用范围进行叙述;对机器学习的不同算法采用统计、图示的方法进行横向比较,得出精确度最高的最优算法;并对以Framingham risk score(FRS)为代表的项目进行简单叙述[5]。
2 分析和结果
2.1 样本大小和时间间隔
在保证其他条件不变的情况下,样本大小和时间间隔决定了模型的拟合程度。研究人员无法确保所获得的样本大小是否影响模型的拟合效果,本文通过对各类文献的研究,探究在保证一定精确度下的最小样本量[18]。时间间隔同样影响着拟合效果,寻找一个在不影响精确度情况下的最小时间间隔会更好地减少时间消耗[20]。
为了获得最小样本量和最小时间间隔,将此模块入选的文献n=43,根据风险预测评估[19]方法的不同分为3 类:机器学习项目[21-22]文献n=18、回归分析项目[23-24]文献n=15、以FRS 为代表的风险预测项目[25-26]文献n=10,针对不同项目采取不同的分析方法。分析样本总量、时间间隔、精确度三者之间的相关性,得到的相关系数如表1 所示。然后对3 类项目分别进行分析,绘制了各自的散点图,如图2~4 所示。删除影响整体分析的数据,建立剩余数据的散点图,如图2(c)、4(c)所示,并对散点图进行趋势性分析。对3 类项目进行描述统计分析,确定各值的意义,具体数据如表2 所示。

表1 相关系数表Tab.1 Correlation coefficients table
表1 列出了样本大小、时间间隔、精确度三者的相关系数。由表1 可见:样本大小与时间间隔相关系数较小,表明两者数据几乎平行,存在微弱相关性,符合通常认定;样本大小和时间间隔分别与精确度存在一定的因果关系,所以合适的样本大小和时间间隔可以影响精确度。
在机器学习项目的样本大小和精确度的散点图2(a)中,点主要分布在精确度为0.8~0.9、样本大小为0~5 000 的区间。进一步分析点密集的地方,在图2(c)中,点主要分布在5 000 左右。在表2 中,关于机器学习项目的样本大小中,中位数为4 103,方差为2.55×108,表明这些数据整体比较离散,采取中位数对这16 个观测数进行统计具有一定的意义。由图2(c)的上升趋势可以得出,为了保证精确度在0.8~0.9 之间,最合适的最小样本量在4 000~5 000 之间。在时间间隔与精确度图2(b)中,点主要分布在精确度为0.8~1.0、时间间隔为5~7 a 的区间,散点图的线性趋势为下降趋势,所以初步得出最合适的时间间隔为5 a。表2 机器学习项目的时间间隔中,方差为1.183,说明数据比较聚集,众数和中位数都为5,综上可得,最合适的最小时间间隔为5 a。
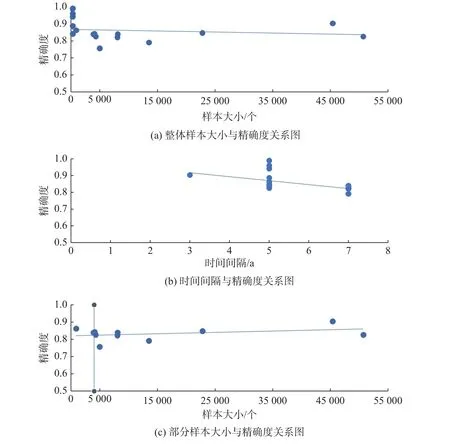
图2 机器学习项目各类散点图Fig.2 Scatter diagram of various types of machine learning projects
在回归分析项目的样本大小和精确度散点图3(a)中,去掉样本的最大值和最小值,点主要分布在精确度为0.75~0.80、样本大小为0~10 000的区间。在表2 回归分析项目的样本大小中,中位数为6 894,方差为1.89×109,数据较分散,点主要分布在4 000~7 000 之间,结合散点图下降趋势,得出在保证精确度较高的情况下,最合适的最小样本量在4 000~7 000 之间。在时间间隔与精确度图3(b)中,精确度为0.75~0.85 之间,时间间隔对应的点较分散,散点图无法得出一个好的结论。表2回归分析项目中,时间间隔平均数为7.267,中位数为6,众数为5,结合这些数据的意义,点主要分布在5~7 a 之间,且最大精确度分布在这个区间。因此,为了提供一个较大的精确度上限,采取的最合适的最小时间间隔为5~7 a。
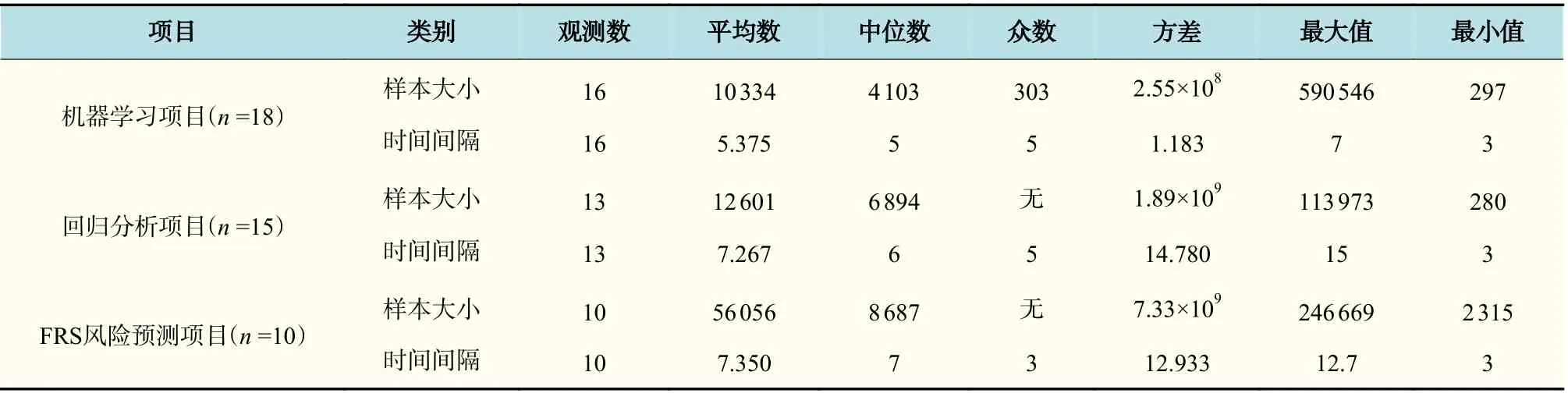
表2 样本大小和时间间隔描述统计表Tab.2 Statistics of sample size and time interval
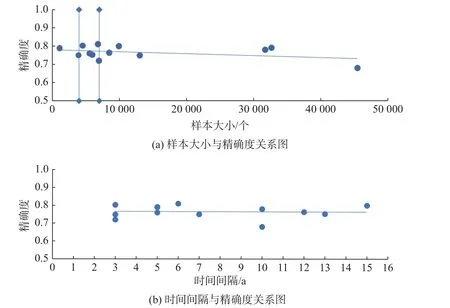
图3 回归分析项目各类散点图Fig.3 Scatter diagram of each type of regression analysis project
在FRS 风险预测项目的样本大小和精确度的散点图4(a)中,点主要分布在精确度为0.70~0.85、样本大小为0~50 000 的区间,但线性趋势呈上升趋势,意味着样本越大精确度越高。在图4(c)中,去掉影响较大的10 万级数据,点主要分布在5 000~10 000 之间,但总体来说精确度相对较小,为保证精确度在0.80 以上,对应的图4(b)中,时间间隔必须为10 a 以上。考虑到图4(a)后半部分精确度较高,无法忽略,在样本大小200 000~250 000、精确度0.80~0.85 之间,这些点对应图4(b)中时间间隔为5~7 a 之间的点。趋势线呈正相关,样本容量越大,时间间隔越大,则精确度越高。所以为了保证精确度在0.80 以上,若采取较小样本量在5 000~10 000 之间,最小时间间隔必须在10 a 以上。若采取大样本量200 000 以上,最小时间间隔建议在5~7 a 之间。
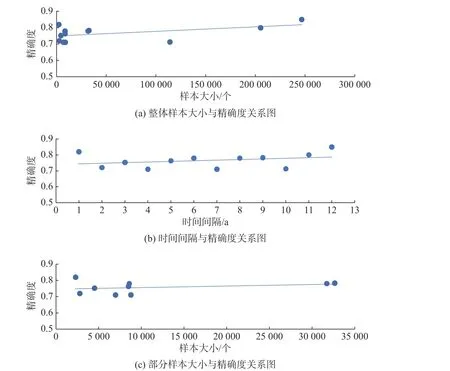
图4 FRS 风险预测项目各类散点图Fig.4 Scatter diagram of various types of FRS risk prediction projects
2.2 数据来源
不同的数据来源提供的医学信息准确性和全面性各不相同,且导致对未来的预测各不相同[19],不同的数据来源获取的困难程度也各不相同[27]。
本文将数据来源模块检索的文献n=50,根据数据获取途径的不同分为4 类:改进电子健康记录(EHRs)[21,28],文献n=10;普通随访调查[26,29],文献n=20;医院体检数据[30-31],文献n=10;UCI机器学习数据库UCI[32-33],文献n=10。为了保证等量对比且数据具有随机性,利用Python 软件的random 函数,从普通随访调查的20 个样本中随机选取10 个样本,将每个序号与列表中的精确度一一对应,形成等量样本。为了探究EHRs 是否改善了精确度,将使用EHRs 与未使用的数据进行对比,如图5 所示。将上述4 类数据来源进行等量对比,经过列表升序和散点图绘制,如图6 所示,得出对精确度综合效果最好的数据来源。
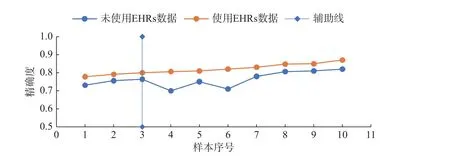
图5 EHRs 使用前后精确度对比图Fig.5 Comparison of accuracy before and after the use of EHRS
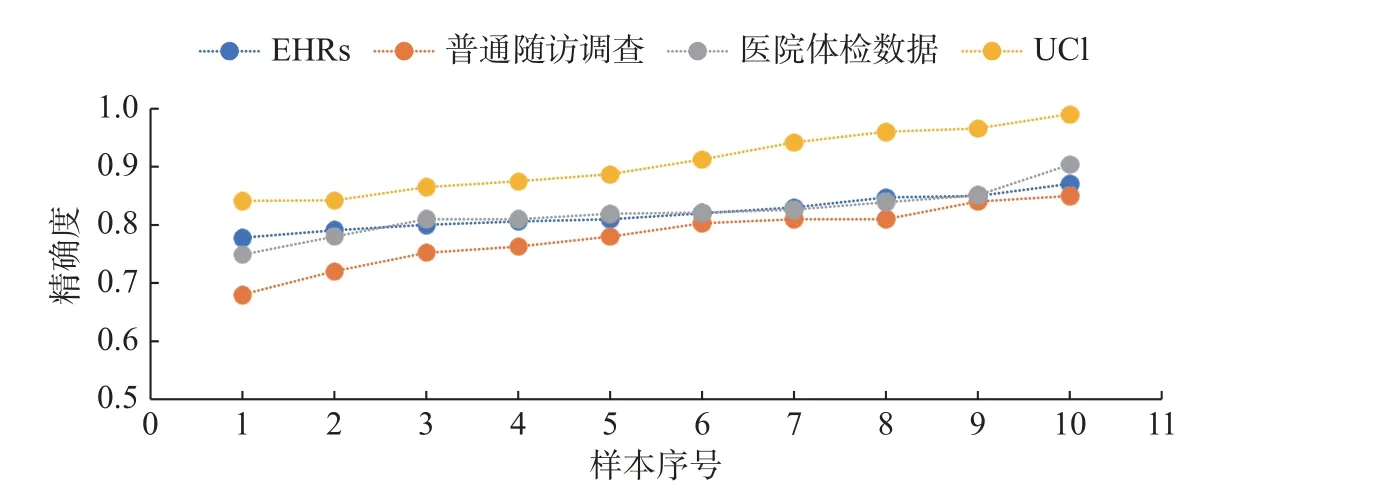
图6 数据来源精确度对比图Fig.6 Comparison of accuracy from different data sources
图5 对比了模型开发过程中EHRs 使用与否的精确度,从图中可以看出,使用EHRs 数据的模型精确度普遍高于未使用的精确度。在使用EHRs 的散点图中,80% 的模型精确度高于0.8。因此,EHRs 的使用可以很好地改善模型的精确度,且保持在一个较高的精确度水平。
图6 将不同数据来源的精确度进行了对比,可以看到采用UCI 的模型其精确度普遍高于其他数据来源,精确度在0.8 以上的点为100%,在0.9 以上的点为50%;采用EHRs 数据和医院体检数据的模型,精确度很接近,在0.8 以上的点为80%;采用普通随访调查的数据,精确度相对较低,在0.8 以上的点为50%,但都低于0.85,且下限值较低。EHRs 具有良好的时序特征,将EHRs应用于机器学习,利用EHRs 数据的高维性,挖掘数据内部关系,可以极大地提高模型精确度[34]。并且,由于EHRs 数据的丰富性,可以在一定程度上减少样本的使用量[4]。医院体检数据具有较高的准确性,但是获取困难,人工处理量大,增加了模型的开发时间。普通随访调查虽然数据获取容易,且可以获得更广大的样本量,但是数据的准确度不高,数据之间的联系较差,人工消耗量较大,针对性不强。所以建议采用EHRs 数据,这样既可以保证模型具有较高的精确度,而且数据获取容易且全面。
2.3 特征
CVD 由多种危险因素引起,更好的特征组合可以实现更加精确的预测效果[27]。不同特征选择方法可以得到不同的特征组合,为了得到最好的特征选择方法,本文将检索的文献n=38 分为3 类:改进特征选择方法项目[27,33]n=12、纳入新特征项目[35-36]n=10、基础特征项目[21]n=16。基础特征包括年龄、性别、血压等目前预测模型中经常采用的特征[24];纳入新特征指在基础特征上,添加了一些研究者认为可能跟CVD 风险相关的危险因素[36],本文将比较纳入新特征前后的精确度,如图7 所示。改进特征选择方法是利用新的算法从数据中挖掘与CVD 有关的特征[37-38],通过列表评分机制,如表3 所示,得出最佳特征选择算法和特征个数。为了消除基数不同产生的影响,采用直方图和精确度等级百分率进行3 类项目对比,如图8 所示,得到最有利于精确度的特征选择方法。
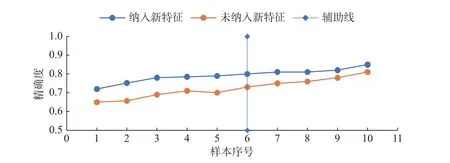
图7 新特征纳入前后对比图Fig.7 Comparison chart before and after the inclusion of new features
图7 将纳入新特征前后的精确度进行了对比,纳入新特征的趋势线始终高于未纳入特征的趋势线,说明在模型中加入新特征可以很好地改善模型的精确度,并且使模型精确度高于0.8 的百分率从10%提高到了50%。
表3 列出了改进特征选择方法的各种算法、精确度以及特征个数,由表3 可得,精确度在0.8 以上的占90% 以上,在0.9 以上的占40%以上,这说明改进特征算法可以很好地提高精确度。在采取的算法中,频数最多的是relief 法和DT 法,都为3,relief 法最大精确度为0.991,DT 法最大精确度为0.966,可以看出采用relief 法和DT 法具有很高的精确度上限,被广泛使用。通过分析,特征个数建议为11~14 个。
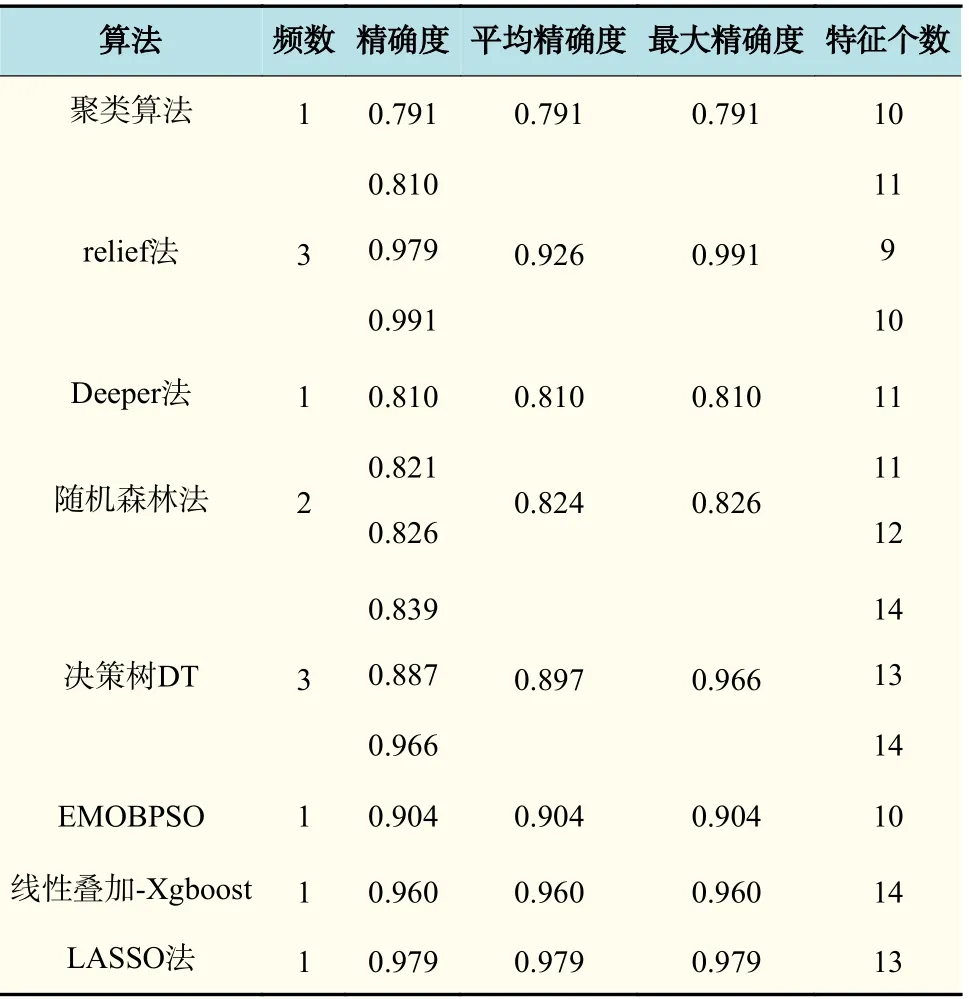
表3 改进特征选择方法列表评分机制Tab.3 List scoring mechanism for improved feature selection methods
在图8 中,直方图显示了各区间的精确度频数,改进特征选择方法项目精确度在0.8~1.0 的占91.67%,0.9~1.0 的占41.67%;纳入新特征项目精确度在0.8~1.0 的占50%,0.9~1.0 的占比为0;基础特征项目精确度在0.8~1.0 的占50%,0.9~1.0 的占比为0,说明改进特征选择算法相比于其他两类项目具有较高的精确度。精确度等级百分率主要反映了各项目的未来潜质,基础特征和纳入新特征趋势线较高的地方主要集中在0.75~0.85之间,在0.85 以上逐渐下降,而改进特征选择方法在0.9 以上仍为上升趋势,具有较好的未来潜质。
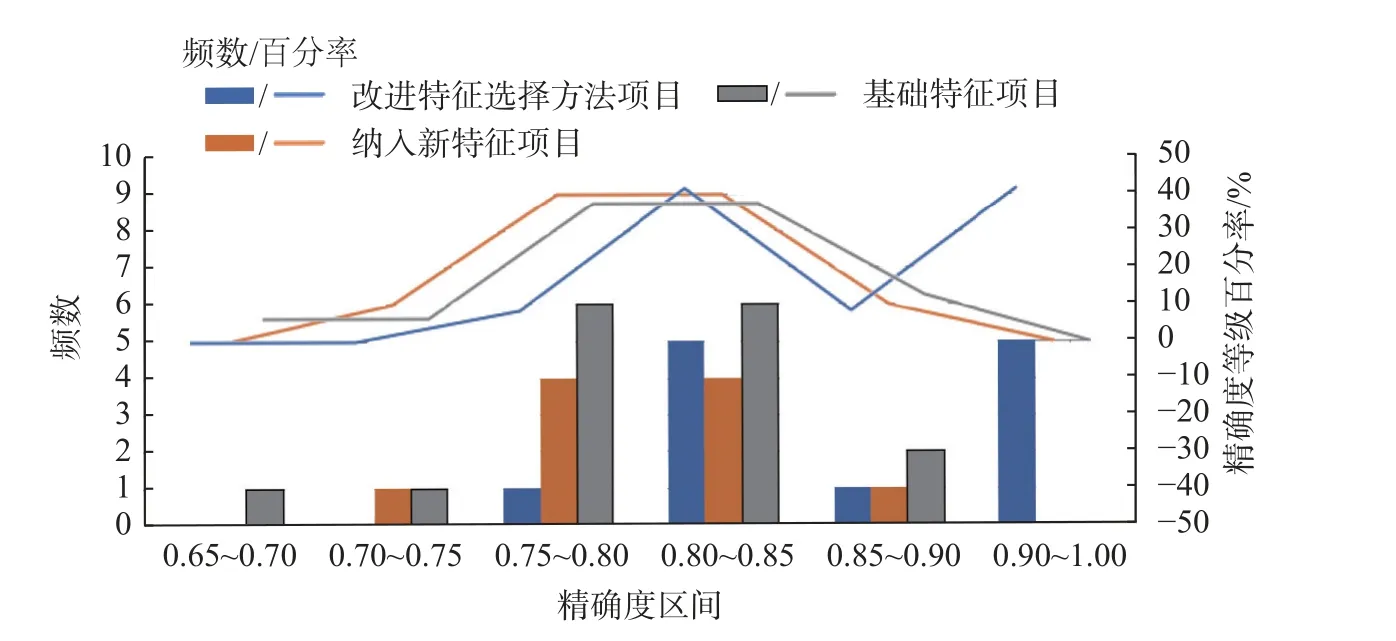
图8 不同特征选择方法的精确度对比图Fig.8 Comparison of accuracy for different feature selection methods
2.4 建模方法
开发模型的目的决定了采用模型的类别,模型类别的选择在一定程度上也决定了模型的精确度。
为了获得精确度更高的建模算法,将n=58 篇文献根据建模目的分为3 类:回归分析项目[36,39]n=26、机器学习项目[33,40]n=28、FRS 风险预测项目[19,26]n=4。回归分析又分为:logistic 逻辑回归,该类别不分析;Cox 比例回归,n=17。采用精确度等级百分率的评分形式,如图9 所示。机器学习项目又分为集成学习、比较多算法、单一算法[27]。集成学习因不同文献之间具有等量类别的相同集成方法,所以采用精确度平均值,对不同集成方法进行精确度比较,如图10 所示。图中:RFBM 表示随机森林Bagging 法;GBBM 表示梯度法;KNNBM表示k近邻Bagging 法;ABBM 表示AdaBoost 提升法;DTBM 表示决策树Bagging法。比较多算法是将每篇文献中最大精确度对应的算法和在所有文献中的使用频数统计出来,如图11 所示。图中:XGBOOST 表示XGBoost 提升算法;DBN 表示动态贝叶斯网络算法;SVM 表示支持向量机算法;LR 表示逻辑回归算法;DL 表示深度学习算法;HTC 表示混合算法。单一算法采用精确度等级百分率进行统计分析;最后采用列表评分机制,对机器学习的各种方法进行精确度百分率比较,如表4 所示。
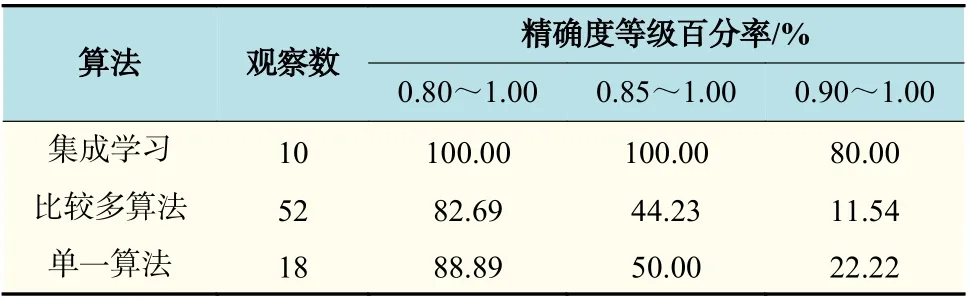
表4 不同算法精确度等级百分率Tab.4 Percentage of accuracy grade of different algorithms
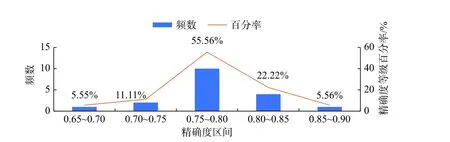
图9 Cox 比例回归精确度等级直方图Fig.9 Histogram of accuracy grade for Cox proportional regression
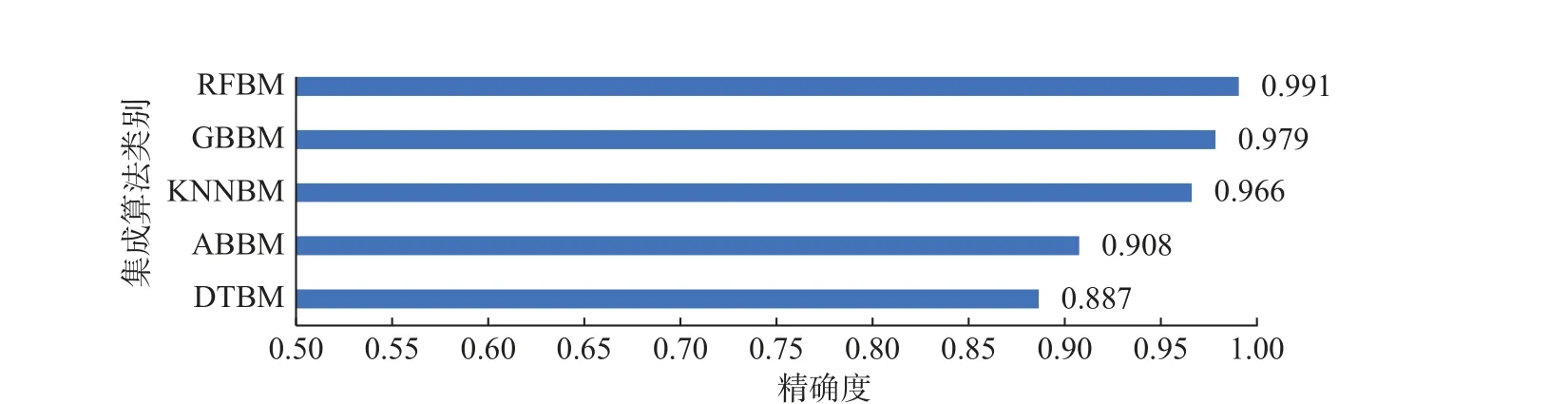
图10 集成算法分布直方图Fig.10 Distribution histogram of ensemble algorithm

图11 比较多算法的最高精确度的频数分布图Fig.11 Frequency distribution chart of maximum accuracy of comparative multiple algorithms
从图9 可以看出,频数主要分布在精确度0.75~0.80 之间,且频数百分率在此区间最大,之后迅速下降,说明采用Cox 比例风险模型精确度普遍较低,这是由于Cox 模型的本质和建模的目的导致的。
集成学习指将Bagging 和Boosting 分类器和各种算法组合在一起的不同算法。图10 展示了不同文献的不同集成算法的精确度平均值分布,从图中得到,精确度都超过了0.85,而采用RFBM 算法精确度高达0.991,接近于1,所以采用集成算法可以很大程度上改善精确度。
图11 是比较多算法类别的直方图和折线图,n=11,将每篇文献精确度最大的算法统计出来绘制了直方图,其中RF 算法的精确度最高,所以采用RF 算法具有较高的精确度上限。SVM 使用次数最多,为4 次,占所统计的36.36%,说明SVM 算法不仅使模型精确度提高而且是广为使用的算法。折线图显示了统计的精确度最高算法在每篇文献中的使用频数,HTC 为1,将其去除,SVM 为10,使用最广。图中列出的这些算法在每篇文献中的使用率达到了75%,甚至100%,除列出的算法外, DT,KNN 也是常用的算法。所以研究者如果采用比较多算法进行建模,建议采用SVM,DBN,LR,DL,RF,DT,KNN 等精确度较高的算法进行比较。
表4 进行了不同算法之间的比较,集成学习类别精确度普遍高于其他两类,而精确度在0.9~1.0 的百分率更高达80%;其他两类算法,精确度在0.8~1.0 相差较小,但单一算法精确度在0.9~1.0 之间的百分率为22.22%,高于比较多算法。因此,从以上分析得出,为了使开发的模型具有较高的精确度,建议采用集成学习。
3 结 论
本研究对检索文献的各个模块进行了详细的审阅和分析,根据探究目的将文献进行不同归类,各类别之间文献有交叉。由于数据的多样性,对不同模块采取不同的数据处理方式,为了消除基数差异影响,本研究创立精确度等级百分率数据评分机制,利用精确度平均法消除不同类别的复杂度,采用random 随机函数保证了获取数据的随机性。最后得到了不同模块对应的建议性改善措施。
在模型中加入新的特征,不仅提高了模型的精确度,更重要是改善了疾病阈值问题,更加细化了高危人群治与不治的难题。利用Cox 比例风险模型,验证了新特征与CVD 的相关性,可以帮助科研人员探求CVD 分子发病机制和基因的靶向治疗。
改进特征选择项目之所以具有较高的精确度,是因为采用特征选择算法能够很好地挖掘样本中的数据,可以从几百个特征中筛选出与CVD极度相关的11~14 个特征,保证了模型与数据的相容性和关联性。而基础特征项目建模前已经确定了各标签,用数据向标签靠拢,发挥不了数据应有的潜力,阻止了数据与模型之间的较好联系,导致精确度往往偏低。纳入新特征项目一般采用Cox 比例风险模型,为了验证新特征与预测结果的关联性,精确度在0.8 左右满足了预测效果。
总的来说,通过对文献各个模块进行数据处理、数据挖掘、图标分析,得到了对模型精确度比较理想的各种改善措施。但是由于时间和人力限制,检索的文献相对较少,即使针对某一模块的文献数量充足,但是将其进行再分类后,各类别数量变得更少。虽然文献数量不影响数据分析,但在一定程度上会影响图形拟合,导致分析结果与事实存在一定误差。综合来看,本文得出的各种改善措施,都可以在一定程度上优化模型,减少模型运行量和时间消耗,对未来研究者开发模型具有重大指导性意义。
