声速剖面未知条件下的平均声速计算方法∗

赵 翀 孙文舟

（1.西安测绘总站 西安 710054）（2.海军大连舰艇学院海洋测绘系 大连 116018）

1 引言

海水声速的变化与温度、盐度、压力有着密切的关系，由于这三种影响因素主要随深度方向发生变化，所以通常的声速剖面仅考虑沿深度方向的变化。Harmonic平均声速的计算方法便是基于这一观点，在已知实测声速剖面的前提下，层内采用常梯度声速模型的方法计算传播时间，从而得出波束经历整个水柱的传播时间和平均声速［1］。因为层内传播时间的计算是在波束垂直发射的情况下，所以声线不发射弯曲。而当入射角不为0°时，声线实际沿弧线轨迹传播而非Harmonic。

平均声速认为的直线传播，因此会带来一定的误差，陆秀平等对此作出了改进［2］，层内传播时间的计算采用圆弧微元代替直线微元，其仿真实验表明，改进后的方法波束脚印位置的计算精度得到提高，对入射角较大的波束改进的效果更加明显。然而这两种方法对平均声速的计算都依赖于实测的声速剖面，而在实际的工程测量中往往仅以某一次的实测声速剖面代表某一海域特定时间段内的声速剖面，由于声速具有空变性和时变性的特点［3］。这种简化方式必然会引起其他时刻的平均声速误差，而且目前尚未有一种在声速剖面未知条件下计算平均声速的方法，通常则采用海水声速的标准值1500 m/s。

针对上述问题本文提出了一种不依赖于声速剖面的平均声速计算方法，该方法基于等效声速剖面法的原理，用某一常梯度声速剖面代替实际声速剖面，通过声波垂直发射到达海底的传播时间计算等效声速剖面的梯度值，进而计算与常声速剖面的相对面积差，利用相对面积差推导得出声源处与测点之间的几何距离，从而得出平均声速值。因为新的方法不依赖于实际的声速剖面，且不受声速时变性和空变性的影响，所以在一些声速剖面无法获得和声速剖面变化剧烈的情况下，本文提出的方法对水下目标定位精度的提高具有重要应用价值。

2 等效声速剖面法原理

根据 Geng Xueyi和Zielinski的观点［4］，具有相同传播时间、表层声速、声速剖面积分面积相同的声速剖面族，其波束脚印位置的计算结果相同。

等效声速剖面法以零梯度声速剖面C0-CA作为参考声速剖面，用常梯度声速剖面C0-CB代替实际声速剖面，相对面积差定义为

相对面积差通过下式计算：

其中εz为垂直位移相对误差，α0为掠射角，ZB0为参考深度，为零梯度声速剖面确定的深度，可以表示为=Z0+c0⋅T⋅sinα0，其中 c0为表层声速，cB为测点声速，T为传播时间，Z0为换能器的吃水深度。

由εs计算等效梯度geq，等效声速剖面对应传播轨迹的曲率半径Req：

测点的掠射角的正余线函数为［5］

垂直位移和水平位移分别为

3 声速空变性对平均声速计算的影响

声速的空变性是指声速在空间各处的数值分布不同，从而导致声速在空间中沿曲线传播，实际的传播平均声速为轨迹曲线段与传播时间的比值。本文计算平均声速采用直线段与传播时间的比值，由此计算的平均声速值定义为有效平均声速，且根据（lurton 2002）、（Xu Peiliang 2005）以及如下的仿真实验验证，有效声速的数值近似于真实的平均声速值［6～7］。

CH为平均声速，pij为i点与j点的实际传播轨迹，f(Xi,Xj)为i点与j点之间的几何距离。

图2 为某一实测的声速剖面，深度3000m，采样间隔为5m，图3是根据常梯度声线跟踪算法计算的实际传播距离与几何距离的误差，在入射角为15°、30°、45°、60°的条件下，平均误差分别为斜距的0.003‰、0.014‰、0.040‰、0.100‰。图4为两种方法计算平均声速的误差，从中可以看出平均声速的误差与入射角度有关，入射角越大，平均声速误差越大，对比图2、3可以得出，平均声速误差还与声速的梯度值变化有关，梯度值越大，两者之间的误差越大，在由负梯度变为正梯度的节点，平均声速误差达到最大。但误差数值都较小，因此用直线几何距离代替实际传播距离计算平均声速的方法所得出的有效声速值近似于真实声速值。

在c1～c8构成的指标体系中，专业素质和科研创新素质可以作为奖励和惩罚的主要依据，也可以作为促进的依据。而德育素质和其他素质可以作为高校进行决策的重要依据。通过分析总体情况和个别学生的综合值，为改进和提高其综合素质提供了良好的基础。

4 不依赖于SVP的平均声速的计算方法

声波在海水中的传播遵循snell法则［8］，如果入射角声波垂直发射，声线将不发生弯曲，此时，等效声速剖面法等价于常梯度声线跟踪法，两种方法计算的声波到达海底的传播时间相等，满足如下公式［9］：

式（11）中仅有geq一个未知数，通过求解该方程即可获得等效声速剖面的梯度值，若垂直波束的传播时间无法获得，则tm可以通过下式近似计算［10］：

根据tm计算相对面积差εs：

等效声速剖面对应传播轨迹的曲率半径Req为

测点处掠射角的正弦函数和余弦函数为

根据式（8）和式（9）分别计算垂直位移和水平位移，则得到换能器与测点之间的几何距离：

由式（10）计算平均声速。

5 仿真实验

5.1 仿真实验一

为验证新方法计算平均声速是否可行，通过仿真实验将新方法与Harmonic平均声速以及常梯度声线跟踪方法进行对比。选用图2声速剖面，水层深度为3000 m，入射角选取范围为0°～60°，每隔5°确定一个入射角，共选取13个入射角。分别用三种方法计算不同入射角条件下平均声速的数值，如图5所示，并以常梯度声线跟踪算法计算的传播时间和平均声速为“真值”，得到新方法在不同入射角条件下的平均声速误差，如图6、7所示，常梯度声线跟踪算法计算波束脚印水平位移和传播时间的公式为

Ch是Harmonic平均声速，Ca是常梯度声线跟踪算法计算的平均声速，Ce是本文提出的新方法计算的平均声速，图5是三种方法计算的平均声速与入射角的关系，若以常梯度声线跟踪算法计算的平均声速为“真值”，新方法与Harmonic平均声速误差随入射角增大而增大。在声波经历的水层深度为3000 m，入射角55°以内时，Harmonic平均声速的误差可以达到0.1 m/s以内，新方法入射角在25°以内时，平均声速误差可以达到0.1 m/s以内，入射角在47°以内时，声速误差在1m/s以内。47°之后误差开始急剧发散。误差的增加主要由两方面原因造成，一是入射角角度的增加引起测距误差的增加，二是在入射角角度增大的情况下，等效声速法计算的直线几何距离误差增大。

图6是三种方法在入射角为0°、20°、40°60°条件下平均声速与深度的关系，图7是新方法计算的平均声速的误差。同样以常梯度声线跟踪算法计算的平均声速为“真值”。入射角为0°时误差均为0，表明三种方法在此条件下是等效的，入射角为20°时，平均声速误差小于0.06 m/s，入射角为40°时，平均声速误差小于0.5 m/s，入射角为60°时，平均声速误差小于4.5 m/s。

5.2 仿真实验二

为验证新方法在水声定位中对测距误差改正的有效性，设计走航式的圆航迹单点水下定位仿真实验。定位方法一般利用GPS技术结合声学测量手段［11～13］，测量船以海底应答器为圆心，水深为半径的圆航迹航行，观测不同时间历元船底换能器到应答器的距离，通过球面交汇的方式确定海底应答器的位置［14～16］，定位的观测方程通常表示为［17］

pi是第i时刻测量船的位置到海底应答器声波的传播距离；f(Xi,Xo)是两者之间的几何直线距离，Xi是第i时刻测量船的位置，Xo是海底应答器的位置；δpdi是由应答器电路延迟引起的系统性误差，一般可以忽略；δpvi是声速变化引起的系统性误差，为主要误差；εi是第i时刻测量的随机误差。

仿真实验采用图2所示的声速剖面，并模拟真实海域，水域潮汐周期为12h，潮高5m，波浪周期为12s，波高2m。水面测量船的位置由GPS确定，定位精度水平方向5cm，垂直方向10cm，测时精度5μs。测量船航行速度为4节（约2m/s），采样周期为10s，共得到945个采样点。测量船到应答器的传播时间可通过实际声速剖面和常梯度声线跟踪算法确定［18～19］。

声速变化引起的测距误差的仿真采用与文献［7］相同的方法，误差共包括4项：1）常数项；2）由短周期内波引起的误差；3）由长周期潮汐引起的误差；4）与测区因素相关的误差：误差的单位为cm。

在测量的时间段内，根据δpv确定各个时刻的真实平均声速和由新方法计算的平均声速如图8所示，Cr为真实的平均声速。由图中可以看出新方法计算得到的平均声速值可以准确地反映真实声速的变化规律。

传统的方法计算pi通常采用表层声速或有效声速与传播时间的乘积确定，本文采用的是有效声速，有效声速是测量船与应答器之间几何距离除以传播时间。新方法采用的是每个时刻的平均声速与传播时间的乘积。分别仿真考虑与不考虑δpv的两种情况。

表1是不考虑δpv，即在观测时间段内声速剖面不发生变化情况下两种方法的计算结果，结果表明两种方法的定位精度基本相同，表2是考虑δpv，即在观测时间段内真实平均声速以图8曲线变化情况下两种方法的计算结果，结果表明新方法的定位精度远高于传统的方法。对比两种情况可得出结论，传统方法的定位精度受声速变化引起的测距误差δpv影响较严重，特别是在垂直方向上，而新方法受δpv影响的程度远小于传统的方法，水平方向仍然可以达到较高的精度，而垂直方向的精度仍然可以达到亚米级。

表1 不考虑测距误差两种方法的定位结果

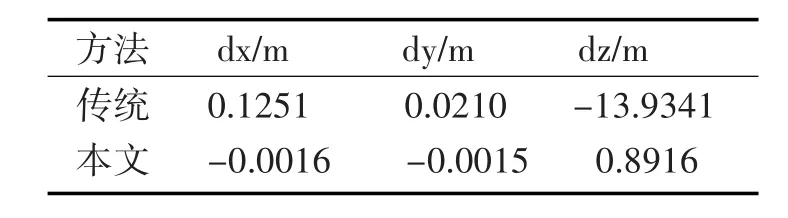
表2 考虑测距误差两种方法的定位结果

6 结语

受洋流、潮汐、海洋表层温度等因素的影响，海水的声速剖面结构不断处于复杂的变化之中，以某一时刻获得的声速剖面结构代替整个时间序列上的声速剖面必然会引入由声速时变性带来的误差，且目前尚未存在一种不依赖于声速剖面的平均声速的计算方法，针对以上问题，本文提出了一种基于等效声速剖面法，利用传播时间计算平均声速的方法，并得出了以下结论。

1）相比于海水标准声速值，本文提出的新方法计算的平均海水声速的精度得到大幅度提高。

2）相比于Harmonic平均声速的计算方法，新方法不依赖于实测的声速剖面，因此省去了测量声速剖面的烦杂过程，大大提高了工作效率。

3）新方法计算平均声速误差与深度和入射角有关，在深度为3000 m，入射角为47°以内。平均声速计算的误差在1 m/s以内。深度为500 m，入射角为45°时，计算误差在0.1 m/s以内。

4）新方法平均声速的计算基于每个时刻声波垂直发射到达海底的时间，不依赖于实际的声速剖面，但可以准确反映声速在时间序列上的变化规律，因此不受声速变化引起的测距误差δpv的影响，从而大大提高了水下目标的定位精度。