基于验前信息的改进Bootstrap导弹命中精度评定方法∗

2018-01-04宋贵宝刘泽坤罗亚民李一夫

舰船电子工程 2017年12期

宋贵宝刘泽坤罗亚民李一夫

1 引言

Bootstrap自助法实质是利用重抽样技术来评估不确定性，利用再生子样对未知参数进行统计推断，其关键在于获得可信程度高的再生子样。Bootstrap自助法是一种对中等数量规模的样本进行统计推断的较优方法，在小子样和特小子样条件下再生子样可信度不高［1］。

新时期条件下，导弹更新换代速度加快、单枚造价高昂。针对导弹命中精度进行的评定试验，现场试验次数和观测数据少，直接运用Bootstrap法，产生的再生子样重复率高，其统计推断结果偏差较大。同时，在导弹生产定型阶段存在着大量的验前信息。如何利用验前信息去扩充现场试验观测样本，改进Bootstrap自助法再生子样的获取方式，提高再生子样的真实程度，是一个值得研究的问题。

基于此，本文针对对地攻击导弹命中精度的评定问题，选取圆概率偏差CEP指标，采用非参数Bootstrap法，通过利用各类通过相容性检验的验前信息来完善现场试验观测样本，并引入重要度抽样的思想，保护更为宝贵的原始观测样本数据，提高再生子样的真实程度和最终评定结果准确性。

2 命中精度评定试验指标

2.1 圆概率偏差CEP

命中精度表现了导弹武器系统弹药相对于固定目标点的落点散布特性，客观反映了导弹武器系统对目标的命中能力。对战术弹道导弹和攻击地面目标的飞航导弹进行命中精度的评定，其实质就是通过获取各类试验信息，对导弹武器系统的命中精度进行统计推断。其中，圆概率偏差（CEP）是导弹武器系统命中精度评定最常用的指标。

圆概率偏差（CEP）指的是在稳定的发射条件下，向目标发射的导弹武器系统，有50%概率落入以期望弹着点（散步中心）为圆心、R为半径的散布圆（等概率圆）内，该散布圆半径R即为圆概率偏差CEP［2］。

针对平面目标射击，以目标为圆心，射击方向为纵轴，垂直于射击方向为横轴，（X，Z）表示落点偏差坐标并服从正态分布，纵横向独立，（X，Z）～N（μX，μZ，σ2X，σ2Z）。如下式所示：

式中，当P=50%时，R即为圆概率偏差CEP；μX、μZ为纵横向射击准确度（系统误差）要求，σX、σZ为纵横向射击密集度（标准差）要求，因此圆概率偏差CEP可综合反映四个指标（μX，μZ，σ2X，σ2Z），能够很好的融合射击准确度和密集度进行表征。

2.2 命中精度纵横向联合检验

从工程应用的角度考虑，对圆概率偏差CEP进行评定，直接寻找相关统计量较为困难。一般来说，由于系统误差可采用各种手段进行补偿修正，当系统误差远小于随机散布偏差时，对导弹命中精度CEP的评定试验，可转化为对射击密集度（标准差）σ的评定。

假定系统误差造成的落点偏差经过补偿修正，射击无系统误差，且落点散布为圆散布。对落点偏差坐标（X，Z），有X ～ N（0，σ2X），Z ～ N（0，σ2Z）。

记σ2X≜DX，σ2Z≜DZ，则对于圆概率偏差CEP的评定，可转化为对射击密集度σ的评定［3］，且当σX= σZ= σ0时，可得：

当σX≠σZ时，可得：

3 Bootstrap自助法

3.1 Bootstrap法原理

设某型导弹靶场试验现场观测i.i.d.样本X=｛X1，X2，…，Xn｝来自未知总体分布，Xi～ F（x），θ=θ（F）是总体分布F的未知数，由子样X1，X2，…，Xn作经验分布Fn，= ( )

Fn为θ的估计，记估计误差：

将估计值 θ(j)(F )作为θ（F）的子样，可作出θ（F）的抽样分布，并由此出发，作出关于θ的统计推断［4～6］。

3.2 再生子样获取的抽样方法

获取再生子样，首先要确定抽样分布函数Fn。根据分布函数Fn中是否含有待定参数，再生子样的抽样方式可分为非参数抽样和参数抽样。这里介绍非参数抽样法。

将获得的i.i.d子样X1，X2，…，Xn按从小到大排序，可得 X=｛X（1），X（2），…，X（n）｝，且X（1）≤ X（2）≤ … ≤ X（n）。可构造经验分布函数如下［7］：

产生服从该经验分布函数的再生子样步骤如下：

每次产生一个［1，n］区间上均匀分布的随机整数η，则可根据η产生新的样本点X（η）；重复该过程n次，可得到一组再生子样X*。

由经验分布函数可知，每个样本点Xi都有相同的被抽中概率，特别是抽样次数很大时，每个样本点的出现频率都趋近于 1/n［8］。

3.3 区间估计

对于参数θ，假定根据Bootstrap法产生的i组再生子样所获得的关于θ的参数估计为j* ，将j*按照大小顺序排列，可得：

因此，给定某一水平α，通过区间截取，可获得置信度水平为1－α的Bootstrap区间估计为

4 小子样条件下改进Bootstrap法

非参数Bootstrap抽样法中产生的新的再生子样均包含在原样本中，且当原样本数量足够时，产生的再生子样中包含有重复子样的概率极低。但是该方法的缺陷在于，当待抽样的原样本的数量较少时，尤其是小子样、特小子样情况下（如n≤5），重抽样的再生子样会出现“退化”现象，即会多次出现两组子样相同的情况［9］。

因此考虑利用可信的验前信息，对现场试验数据进行补充，扩大待抽样的原样本容量，并引入重要度抽样的思想保护现场试验数据，提高Bootstrap方法产生的再生子样与真实分布的相符合程度。

4.1 验前信息相容性KS检验

导弹在生产定型等过程中的验前信息种类繁多。在应用这些验前信息前，必须对验前信息和现场试验信息进行相容性检验，本节采用KS检验法。

假定有来自于总体分布F（x）的样本：

其经验分布函数为Fm（x）。

另有来自总体分布G（y）的样本：

其经验分布函数为Gn（y）。

取检验统计量

并给定显著性水平α，若

则可认为两样本不属于同一总体，否则属于同一总体。式中

Dl，α可通过查找柯尔莫格洛夫检验临界值表得出。

4.2 基于验前信息的改进Bootstrap抽样

假定有n组现场观测数据为

且(Xi，Zi) ～ N（0，0，σX2，σZ2）。另有NF组已经通过显著性水平为α的KS检验的验前信息落点偏差数据为

为避免现场试验数据被大量验前信息所“湮没”，引入重要度抽样的思想［10～11］，根据不同类信息源的临界检验水平αL（即超过该水平无法通过相容性检验）来映射信息源的置信度ωi。

工程上相容性检验的水平一般取0.1～0.4，因此采用以下从临界检验水平αL到置信度ωi的线性映射：

假定存在p类验前信息源，每类信息源的临界检验水平为 αL(i)（i=1，2 ，…，p），则有线性映射：

根据置信度确定重要度。先令现场试验子样本的置信度ε0为1，则p类验前信息源的重要度为

将上述两组数据相混合，可以得到能够产生再生子样X*的待抽样样本：

现场试验子样本的重要度为

4.3 改进区间估计法

针对传统区间估计方法估计效率不高，且总体分布非对称时效果不佳的不足，本节采用Bootstrap-t区间估计法。

Bootstrap-t区间估计相关步骤如下：

1）根据观测子样X获得参数θ的估计值和标准差 se()；

2）由经验函数再抽取k组再生子样本为

并由各子样本分别获得估计值 *i和估计标

3）取统计量

并根据大小顺序排列 t*i，得到

则给定某一水平α，通过区间截取，可获得置信度水平为1－α的Bootstrap区间估计为

5 实例分析

某型对地攻击导弹进行命中精度评定，经过现场靶场试射，得到5组真实纵横向落点偏差值数据，且服从正态分布N（0，502），具体数据见表1。

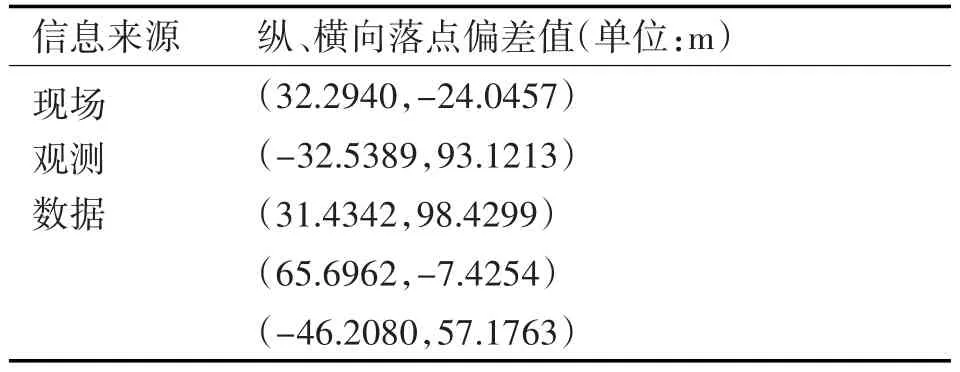
表1 现场观测样本数据

另有两类通过了KS相容性检验的验前信息，一类是改进前相似型号试射的6组验前数据（临界检验水平αL1为0.1），另一类是模拟弹道仿真试验的6组验前数据（临界检验水平αL2为0.2），两类验前数据均服从正态分布N（0，552），具体数据见表2、表3。

根据式（16）线性映射，可得相似型号试射信息的置信度为1/2，弹道仿真信息的置信度为2/3；

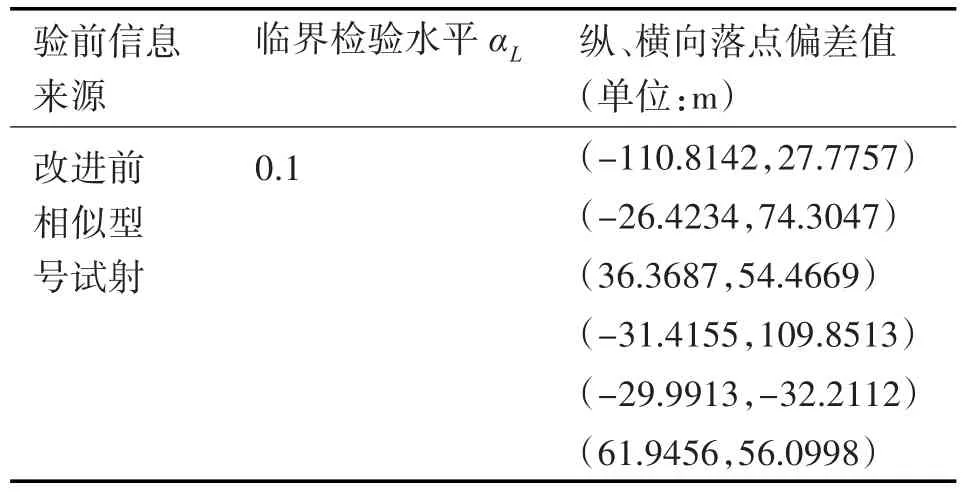
表2 改进前相似型号试射验前信息数据

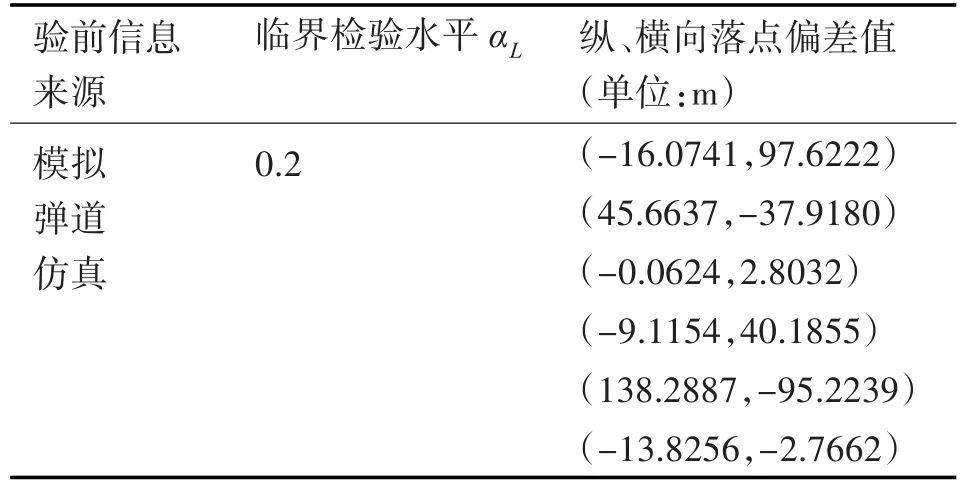
表3 模拟弹道仿真验前信息数据

根据式（17）、式（18），可得相似型号试射验前信息分配权重为

弹道仿真信息分配重要度为

现场真实数据分配重要度为

因此，相似型号试射验前数据的6个子样本每个被抽中概率约为0.038；弹道仿真信息的6个子样本每个被抽中概率约为0.052；现场真实数据5个样本，每个被抽中的概率约为0.092。

根据图2仿真步骤进行抽样，设定再生子样的容量为20（即每20个新产生的数据为一组再生子样），共抽取2000组。由获得的子样本相关数据，分别进行纵、横向射击密集度（标准差）点估计、置信度80%的区间估计以及计算圆概率偏差CEP值。仿真步骤如下：

根据仿真流程，所获得的仿真结果与分析结论如下：

1）基于验前信息的改进Bootstrap法与经典统计方法的仿真结果见表4。

分析可知，经典统计方法直接应用现场观测样本与验前信息共17个样本数据，该方法并不产生再生子样，其σX与σZ的点估计要大于采用重要度抽样的自助法的σX与σZ的点估计，且经典统计方法区间估计远不够精确，如σX的80%置信区间估计，经典统计方法的［46.4407，73.8400］区间范围远大于自助法的［42.3384，61.5753］区间范围；

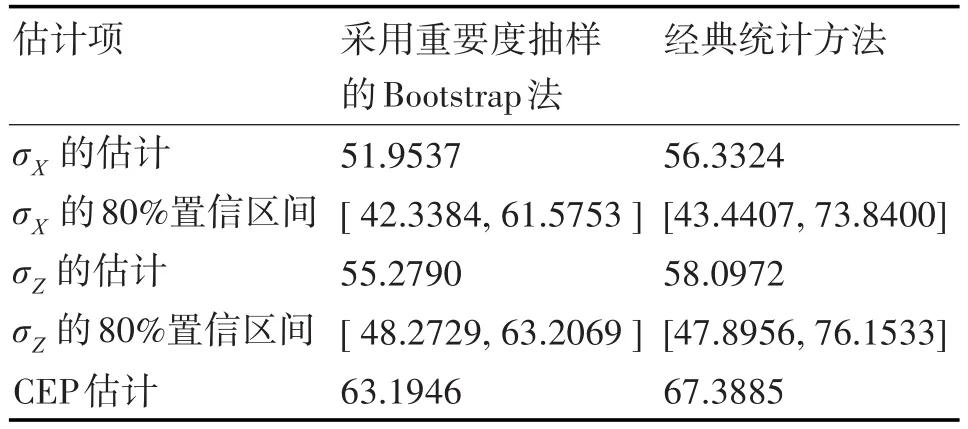
表4 纵、横向射击密集度σ估计结果（1）

2）采用重要度抽样的Bootstrap法与不采用重要度抽样的Bootstrap法的统计推断数据见表5。

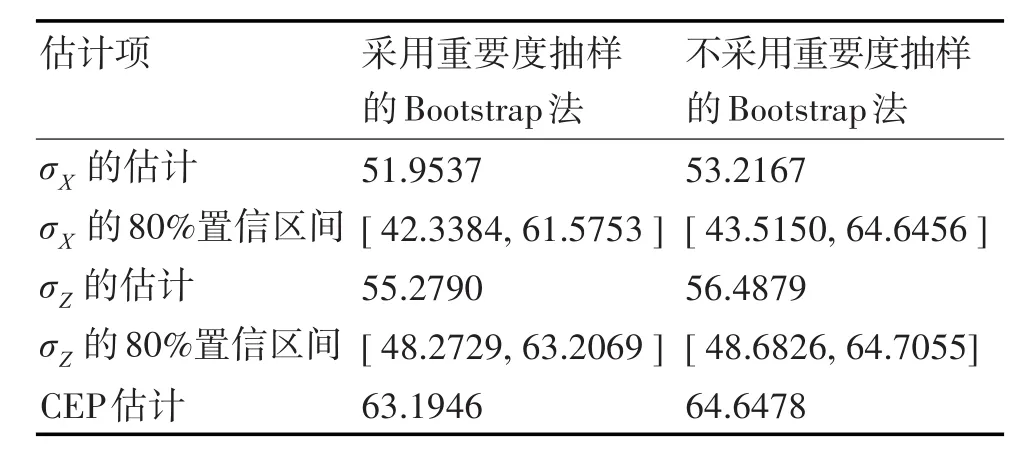
表5 纵、横向射击密集度σ估计结果（2）

分析可知，相比于不采用重要度抽样，采用重要度抽样的评估结果更接近现场观测样本的分布特征，如σX的点估计51.9537更接近σ0的估计值50；σX的80%置信区间估计［42.3384，61.5753］比区间［43.5150，64.6456］更接近正态分布 N（0，502）；

3）射击密集度σ分布（以σX为例）见下图3、4。

分析可知，采用重要度抽样的改进自助法，其射击密集度σX的区间（总体）分布更近似于正态分布，且σX的点估计和区间估计，更接近于现场观测样本的分布N（0，502），其真实性和可信程度更好。

综上可知，在小子样条件下，基于验前信息的改进Bootstrap法所产生的再生子样，其可信程度比改进前Bootstrap法产生的再生子样可信度更高，其统计推断结果相比于经典统计方法也更加得精确，因此该方法能够为小子样条件下导弹命中精度的评定提供一种可供参考的结果。

6 结语

本文结合某型对地攻击导弹的现场试验数据，选取射击密集度σ作为命中精度评定指标，针对非参数Bootstrap法不适用于小子样条件下统计推断的缺陷，通过综合利用各类真实的验前信息数据，引入重要度抽样思想，对Bootstrap再生子样的获取方式进行改进。仿真结果表明，基于验前信息的改进Bootstrap法所获得的σ估计与置信区间，其结果的真实性更好，能够为导弹命中精度评定试验提供一定的参考。

当然，Bootstrap自助法作为一种原始样本信息的“提携”手段，在小子样甚至特小子样条件下应用，存在着许多可以改进之处。如现场数据的大致分布已知时能否采用参数Bootstrap法（原始样本仍是小子样条件），落点纵横向偏差非独立时如何应用验前信息，各类验前信息的重要度如何更好地进行分配，再生子样的容量如何设定才能更加合理等。这些问题值得进行更为深入地研究。

［1］唐雪梅，蔡洪，杨华波等.导弹武器精度分析与评估［M］.北京：国防工业出版社，2015：250-263.

［2］王正明，卢芳云，段晓君等.导弹试验的设计与评估［M］.北京：科学出版社，2010：438-440.

［3］张宗梅，宋维军，李双喜等.一种融合验前信息的特小子样精度评估方法［J］.航天控制，2011，29（6）：49-53.

［4］Davison，A.C.（Anthony Christopher），Hinkley，D.V.Bootstrap Methods and Their Application［J］.Technometrics，1997，42（2）：216-217.

［5］雷鸣，张丽群.基于Bootstrap方法的舰空导弹武器系统制导精度评定［J］.现代防御技术，2014，42（5）：60-64.

［6］刘新爱，陈勇男，王如根.基于自助法的导弹命中精度评定［J］.战术导弹技术，2004（06）：32-34.

［7］孙锦，李国林等.基于Bootstrap的反舰导弹靶场试验小样本数据分析方法研究［J］.计算机与数字工程，2014，42（1）：48-51.

［8］Pérez M C I，Manteiga W G.Bootstrap for the conditional distribution function with truncated and censored data［J］.Annals of the Institute of Statistical Mathematics，2003，55（2）：331-357.

［9］刘思雨，张敏强.Bootstrap平均数假设检验样本容量探讨［J］.统计与决策，2016（14）：26-28.

［10］唐雪梅，李荣，胡正东等.武器装备综合试验与评估［M］.北京：国防工业出版社，2013：33-82

［11］胡正东，曹渊，张士峰等.特小子样试验下导弹精度评定的Bootstrap方法［J］.系统工程与电子技术，2008，30（8）：1493-1497.

［12］刘建，吴翊，谭璐.对Bootstrap方法的自助抽样的改进［J］.数学理论与应用，2006（1）：71-74.

［13］Duan X.APPLICABILITY OF BOOTSTRAP METHOD IN SMALL SAMPLE CASE［J］.Journal of Ballistics，2003（3）：1-5.

［14］金振中，李晓斌等.战术导弹试验设计［M］.北京：国防工业出版社，2013：96-143

［15］郭齐胜，罗小明，潘高田.武器装备试验理论与检验方法［M］.北京：国防工业出版社，2013：188-191.

［16］GJB5207-2004.地地战术导弹批抽检飞行试验验收方法［S］.国防科学技术工业委员会批准，2004.

［17］GJB2899-97.飞航导弹飞行试验精度分析和命中精度评定方法［S］.国防科学技术工业委员会批准，1997.

［18］樊立明，吴鹏，万伟.基于Bayes自助法的小子样命中精度评估［C］//The International Conference on Computational Intelligence and Industrial Application.2010：3-4.

［19］曹裕华.装备试验设计与评估［M］.北京：国防工业出版社，2016：183-189.

［20］徐英，王松山，柳辉等.装备试验与评价概论［M］.北京：北京理工大学出版社，2016：29-46.