多元问题的处理策略

李昊哲

(河北省衡水市第一中学 053000)

多元问题的处理策略

李昊哲

(河北省衡水市第一中学 053000)

在高考及数学竞赛中，一些较难的题目往往是以含参数问题或多元形式出现，学生对这类题目常常难以入手.本文就多元问题的几种思维途径加以论述，有益于解题能力的提高.

多元问题；处理策略；主元

数学中有一类涉及多个变元的问题.由于变元多，难以找到解题的切入点，本文结合实例给出几种处理方法.

一、减元(消元)

面对多个字母，最基本的想法就是减元(消元)，转化为两个甚至一个字母的问题，从而简化问题，明确解题思路.

例1 已知非零实数a、b、c、d满足条件：a、b是方程x2+cx+d=0的两个角，c、d是方程x2+ax+b=0的两个角，求a、b、c、d的值.

解利用韦达定理，由a、b是方程x2+cx+d=0的两个角，知a+b=-c,ab=d,即c=-(a+b),d=ab.

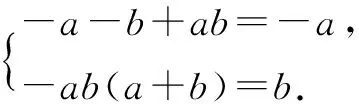
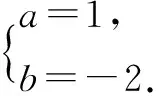
综上，a=1,b=-2,c=1,d=-2.

点评本题若依常规，按解的定义把a、b，c、d分别代入两个方程，将得到一个四元高次方程组，难以继续求解.而本例解法，把c、d都用a、b来表示，从而减元为二元(关于a、b)的问题，降低难度，方便获解.

二、构造方程

特别是构造出一元二次方程，用判别式来求解.

例2 设实数a、b、c满足a+b+c=0,abc=1,求a、b、c中最大者的最小值.

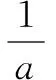
点评本例也可用关于b、c的均值不等式来求出a的取值范围.

三、用均值不等式

用均值不等式取等号的条件，求出各字母的数值，从而获解.

例3 设实数x、y、z满足条件y=6-x,z2=xy-9,求x、y、z的值.

解由已知条件有x+y=6>0,xy=z2+9>0,知x、y都是正数.

所以x=3,y=3,z=0.

点评本例也可由x+y=6,xy=z2+9，知x、y是关于u的一元二次方程u2-6u+z2+9=0的两个实根，再由Δ≥0，及取等号条件求出z及x、y的值.

四、变更主元

在以某个变元为主元的多元问题中，按常规方法从主元入手分析求解，有时比较困难.此时不妨转换思维方向，以某个次元为主元重新思考，往往会割然开朗，获得新颖简捷的解法.

例4 当-1≤k≤2时，不等式kx2-x-k-1<0恒成立，求x的取值范围.

五、确定主元

对于某些地位均等的多元问题，不妨认定其中一元为主元，往往能打开解题思路.

思路先消去z，再以x为主元，用判别式法求出y的范围.

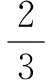
[1]史庆华.例说多元函数最值的求解策略[J].中学生数学(高中)，2010(10)：38-39.

[2]林国夫.二次型约束下最值的求解策略[J].中学生数学(高中)，2010(11)：28-30.

[3]蔡勇全.多角度解析一道高考填空题[J].中学生理科应试，2015(4)：7.

[4]姜国庆.三类非线性多元函数最值问题的图象解法[J].高中数学教与学，2014(1)：14-15.

G632

A

1008-0333(2017)31-0038-02

2017-07-01

李昊哲，河北省衡水第一中学，高三学生.

杨惠民]