新型余弦齿轮运动仿真分析
2017-12-28许彩云
王 伟,许彩云
(闽南理工学院工业机器人测控与模具快速制造福建省高校重点实验室,福建 石狮362700)
新型余弦齿轮运动仿真分析
王 伟,许彩云
(闽南理工学院工业机器人测控与模具快速制造福建省高校重点实验室,福建 石狮362700)
基于Pro/ENGINEER Widefire操作平台,研究新型余弦齿轮的实体建模与运动仿真。介绍了余弦齿轮的齿廓曲线方程,推导了余弦齿廓的共轭齿面方程,建立了完整的余弦齿轮三维实体模型,并就一对余弦齿轮副进行运动仿真分析。通过仿真结果可以快速、准确地检测余弦齿轮副之间的干涉、运动特性,对提高余弦齿轮的设计和制造效率有一定的指导意义。
余弦齿轮;实体模型;运动仿真
受Logix齿轮[1]、双渐开线齿轮[2]等新型齿轮的启发,为了克服齿轮在齿轮泵的应用过程中存在的某些缺陷[3],如容积效率低、流量小和困油现象等,提出了一种新型齿轮传动方式——余弦齿轮传动。余弦齿轮的齿廓曲线是一条余弦曲线,由凸曲线和凹曲线两部分组成。余弦齿廓中间部分曲率半径很大,有利于提高接触强度,能保证共轭齿廓的正常啮合性能,可广泛应用于齿轮泵等领域,对缓解齿轮泵的困油现象、提高其容积效率、增大其流量和压力等具有积极的意义。
在真实余弦齿轮加工前,运用Pro/ENGINEER软件,可以精确地建立其三维实体模型,而后转化到动力学仿真环境下,添加复杂的力和约束,然后进行运动仿真分析,通过仿真结果,可以检测齿轮传动过程中的齿廓干涉和连续传动情况,然后快速、准确地修改模型,从而缩短修改时间,提高设计效率。对提高余弦齿轮的设计和制造效率有一定的指导意义。
1 余弦齿廓曲线和共轭齿廓方程的推导
1.1 齿廓曲线方程
余弦齿轮的齿廓与双圆弧齿轮的特征相似,都是齿顶部凹,齿根部凸,其齿廓曲线如图1所示,在极坐标下,齿轮齿廓的极坐标方程[4]为:
ρ= r+Acos(zφ)
其中,A为振幅,r为分度圆半径,z为齿数,z= 2πr/p.
其参数方程为:


图1 齿廓曲线方程
1.2 共轭齿廓方程
如图2所示,设坐标系Σ0(O:x,y)为静坐标系,其原点O与啮合点P相重合,坐标系Σ1(O1:x1,y1)与齿廓C1相固连,坐标系Σ2(O2:x2,y2)与齿廓C2相固连,O1和O2分别为Σ1和Σ2的原点。在坐标系Σ1中,齿廓C1的方程[5]为:


图2 齿轮啮合坐标系
为了推导齿廓C2的参数方程,将啮合点在坐标系中的径矢由坐标系直接变换到坐标系下:

其中,φ1、φ2分别为齿轮1和齿轮2转过的角度,φ2=i*φ1,i为齿轮传动比,a为齿轮中心距。
如图3所示,齿轮1的瞬心线是半径为r1的圆,p为瞬心点,它在固定坐标系1中的位置是一定的,已知的齿形a-a与坐标系固联在设齿形a-a上任意一点m1(x1,y1)处的切线与x1轴的夹角为β,又由O1作m1p1的垂线,并设它与O1p1的夹角为ψ,则由图3可知。
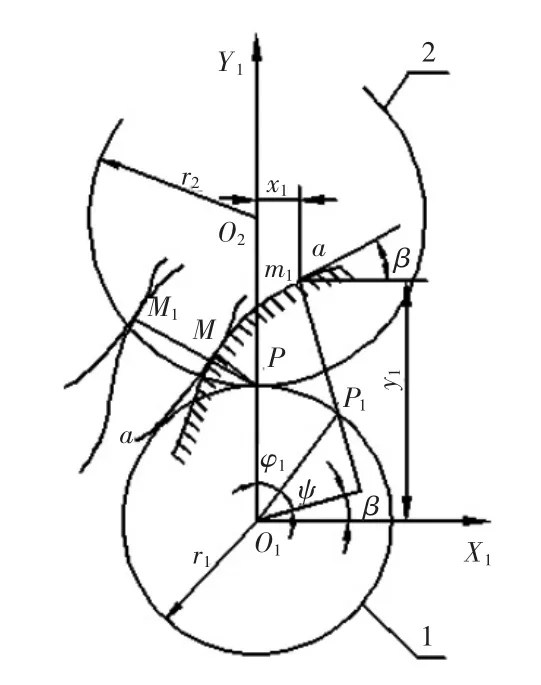
图3 共轭齿廓的计算参数
其中:p点为a-a上M点的法线与Y1交点;p1点为齿形上点m1的法线与节点的交点。
联立式(1)、式(6)和式(7)就可求得齿廓 C2的方程。其共轭齿廓的形状,也是一条近似余弦形状的曲线。
2 齿轮实体模型的建立
轮齿部分是齿轮中最复杂的部分,余弦齿轮同其它齿轮一样,为了满足运动仿真分析、有限元分析等的需要,要求精确绘制出其三维实体模型。本文以齿数z1、模数m=3 mm、压力角α=20°齿宽b=30 mm的余弦齿轮(规定为齿轮1)为例,配对齿轮2z2=28,基于Pro/Engineer操作软件,按照渐开线齿轮的三维模型的建立方法[6],叙述齿轮1和其共轭齿轮(规定为齿轮2)实体模型的构造过程。
2.1 齿轮1的实体模型
用Curve/From Equation命令在cartesian坐标系下输入如下方程,获得齿轮1的一条余弦曲线方程。

通过Mirror命令获得另一余弦曲线,为了保证齿轮副在啮合过程中不出现啮合干涉,齿轮1和2的齿顶均用一段与余弦曲线相切的圆弧来过渡,考虑到齿轮副之间的油膜厚度[7],该圆弧的半径取1.
用Extrude命令生成单个轮齿,Pattern命令生成齿轮1的毛坯模型,用Cut命令生成键槽,得到齿轮1的三维实体模型如图4所示。

图4 齿轮1实体模型
2.2 齿轮2的实体模型
由于共轭齿廓的曲线方程比较复杂,按照齿轮1中生成余弦曲线的方法很难实现。利用Matlab软件,在共轭齿廓上取20个点,然后通过点连成线,获得齿轮2的齿廓,最后按照与齿轮1同样的方法建立齿轮2的三维实体模型,如图5所示。

图5 齿轮2实体模型
3 余弦齿轮副啮合仿真分析
以一对齿轮副为例(z1=20,z2=20,m=30 mm),进行齿轮副啮合仿真分析。图6为齿轮啮合仿真界面,图7所示为单个轮齿齿廓啮合接触区形状。
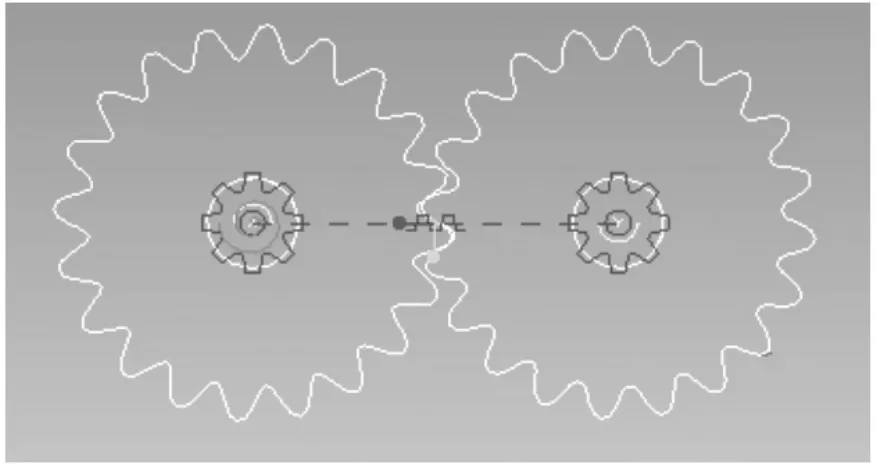
图6 啮合仿真界面
图7 齿轮副接触区形状图
由图6、图7可知:
(1)仿真结果表明齿轮副无啮合干涉现象,并能连续传动。
(2)齿轮副接触形状为直线,从而可以推断余弦齿轮传动形式为线接触。
4 结语
本文建立了余弦齿轮的齿廓曲线方程,运用齿轮啮合原理和微分几何方法,推导了其共轭齿廓方程,利用Pro/ENGINEER的建模功能,生成一对余弦齿轮副,并仿真其啮合过程。仿真结果表明余弦齿轮副在啮合过程中不存在啮合干涉,能实现连续传动,传动形式为线接触。
[1]Komori T ,Ariga R,Nagata S.A New Gear Profile Having Zero Relative Curvature at Many Contact Points[J].Transactions of the ASME,1990,12(3):430-436.
[2]张光辉,李凤吉,魏 静.分阶式双渐开线齿轮啮合特性及有限元研究[J].机械传动,2008,32(5):1-5.
[3]栾振辉.齿轮泵研究的现状与发展[J].起重运输机械,2005(6):11-13.
[4]Thomas Yeh ,Daniel C.H.Yang,Shih-His Tong.Design of new profiles for high-load capacity gears[J].Mechanism and Machine Theory,2001(36):1105-1120.
[5]S.Barone.Gear Geometric Design by B-Spline Curve Fitting and Sweep Surface Modeling[J].Engineering with Computers,2001(17):66-74.
[6]冀 斌,王春燕,卢丽娟,等.基于Pro/E双圆弧齿轮参数化建模及虚拟装配仿真[J].太原科技大学学报,2016,37(1):50-53.
[7]赵 宁,贾清健,欧阳斌,等.基于润滑承载接触分析的直齿轮滑动摩擦效率研究[J].机械科学与技术,2015,34(3):329-333.
Study on Dynamic Simulation of New Cosine Gear
WANG Wei,XU Cai-yun
(Minnan University of Science and Technology,Industrial Robot Measurement and Control and Mold Manufacturing of Key Laboratories in Fujian Province,Shishi Fujian 362700,China)
Based on Pro/Engineer,the 3D model of cosine gear is built,and the dynamic simulation is studied.In this article,the profile curve equation of cosine gear is introduced,and the conjugate equation is deduced.The 3D model of a pair of gears is built,and the dynamic simulation is studied.From the result of simulating,it can detect the interference and the dynamic characteristics of a pair of cosine gears quickly.It is significant to improve the efficiency of design and manufacturing of cosine gear.
cosine gear;solid model;dynamic simulation
TH132.41
A
1672-545X(2017)10-0009-03
2017-07-07
泉州市科技计划项目(2014Z140);石狮市科技计划项目(2014SK12);工业机器人测控与模具快速制造福建省高校重点实验室项目(闽教科〔2017〕8号)资助
王 伟(1984-),男,江西婺源人,工学硕士,讲师,研究方向:精密加工技术,机械传动新技术。
