计及框架参数的动力吸振器建模与优化研究

王家璇，曹远鹏，黄其柏

（1.华中科技大学机械科学与工程学院，湖北 武汉430074；2.湖北省专用汽车研究院，湖北 随州441300）

计及框架参数的动力吸振器建模与优化研究

王家璇1，曹远鹏2，黄其柏1

（1.华中科技大学机械科学与工程学院，湖北 武汉430074；2.湖北省专用汽车研究院，湖北 随州441300）

传统的动力吸振器理论模型多为二自由度系统，由于在工程应用中，动力吸振器安装框体质量、刚度对系统会产生影响，使其动力学模型更接近于三自由度。本文建立了三自由度动力吸振模型，比较了二、三自由度模型的差异。利用MATLAB中的遗传算法模块对模型中的两个待定参数进行了编程优化，得到了动力吸振器在最优参数下的减振特性与效果。

动力吸振；三自由度；动力放大系数；遗传算法

动力吸振器（Dynamic vibration absorber，DVA）是抑制结构或系统共振，降低周期性噪声的有效手段，时至今日，国内外对此进行了大量的研究[1-2]。传统的动力吸振器通常采用二自由度系统，忽略了动力吸振器框架质量和刚度对系统特性的影响，致使动力吸振器在实际使用过程中设计的吸振频率与实际中存在差异，特别是当被吸振体质量较轻或连续系统动力吸振时，其差异更为明显。因此，研究考虑动力吸振器质量、刚度的三自由动力吸振系统模型，将更接近于实际情况。

本文将类比传统的二自由度动力吸振模型，推导考虑框架等效质量和刚度的三自由度系统中动力吸振模型，分析在相同参数情况下两种模型动力放大系数的差异。在此基础上应用MATLAB的遗传算法模块进行编程，通过仿真计算与参数优化，得到动力吸振的优化特性，验证优化前后的动力吸振效果。

1 动力吸振器模型

1.1 传统的两自由度动力吸振模型

传统DVA多采用二自由度模型，其结构如图1所示。

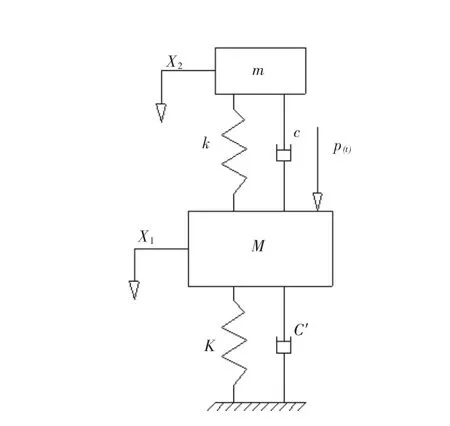
图1 传统二自由度模型

其主系统M对于激振p(t)的动力放大系数公式为[3]

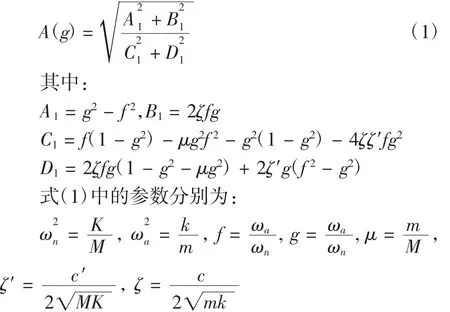
1.2 计及框架参数的动力吸振模型

当考虑DVA安装框架的质量和刚度时，其动力吸振系统模型可表示为如图2所示的三自由度系统，其中m2表示外框质量，k2则表示外框与主系统的连接刚度。由振动理论可得图2所示系统的运动微分方程组为：

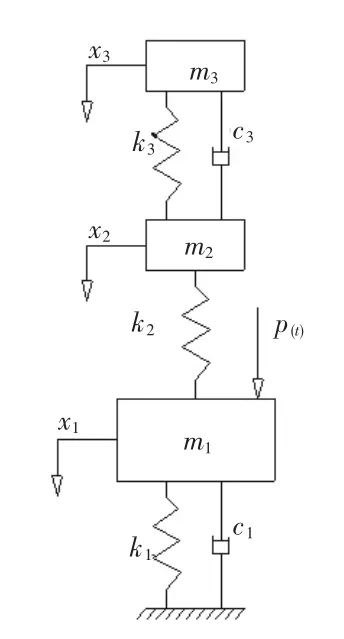
图2 三自由度模型

因而其传递函数矩阵G（jω）的表达式为：

式中的Aij表示矩阵D（jω）第i行，第j列的代数余子式。因而通过化简，可以得出质量块m1的位移对于作用于其上的激励力p(t)的传递函数表达式为：

1.3 两种模型的比较分析

若动力吸振系统为两自由度模型，其外框质量是直接加在被吸振体上的，即m2与m1合为一体，连接刚度k2趋于无穷大。为了分析两自由度动力吸振模型与三自由度动力吸振模型的差异，比较框架连接刚度对吸振特性的影响，本节拟从外框刚度较大（f2=10）与较小（f2=1）两种情况进行分析。

当动力吸振器外框刚度较小（f2=1）时，两自由度系统模型与三自由度系统模型的动力放大系数如图3所示。由图可知，采用三自由度系统，其动力放大系数有三个明显的峰值，与两自由度模型差异较大。

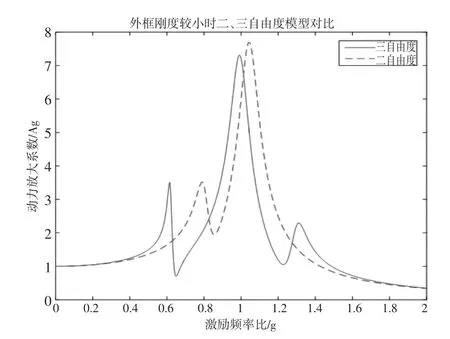
图3 外框刚度较小（f2=1）时对比图

当外框刚度较大（f2=10）时，此时外框质量将接近于叠加于主振系上，此时三自由度系统逼近于两自由度系统。为了验证这种情况下二自由度吸振模型与三自由度吸振模型的差异，针对两种模型，选取相同质量、刚度参数，其中二自由度模型将外框质量直接等效到主系统上。通过仿真计算可得其吸振系统动力放大系数曲线如图4所示。

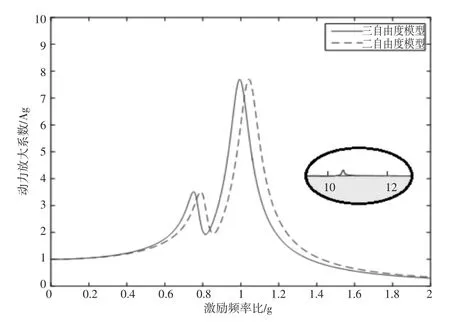
图4 外框刚度较大（f2=10）时对比图

由图4可知，两自由度系统和三自由度系统均只显示了两个主要峰值，但三自由度系统的两个主要峰值频率比两自由度系统要低，三自由度系统的第三个峰值出现的频率偏高，峰值较小。

图5所示为f2取值逐渐增大时的曲线变化趋势图。对于三自由度模型，随着k2值的增大，其动力放大系数曲线与两自由度的峰值逼近。

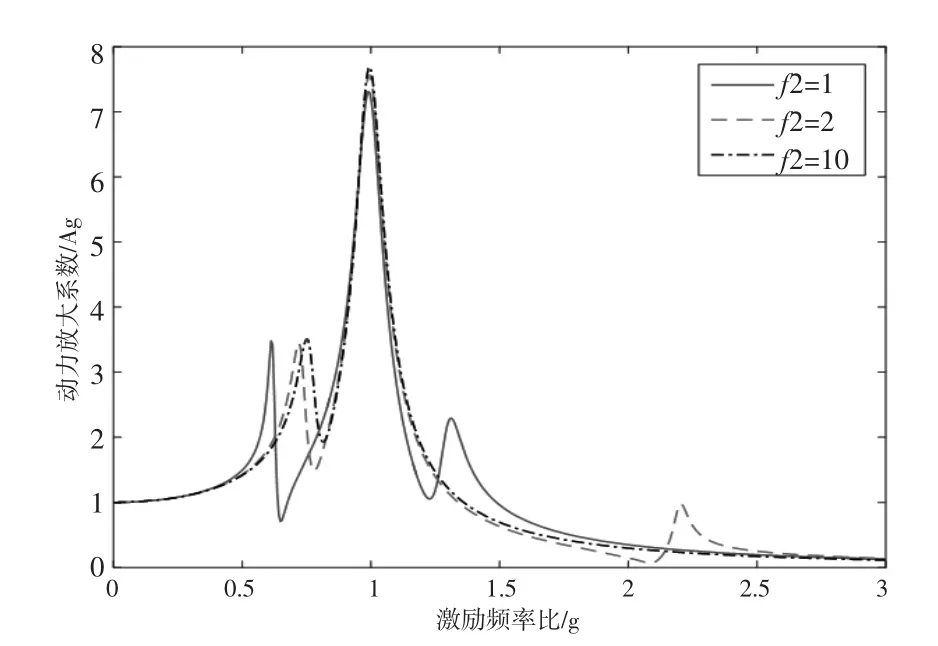
图5 不同取值下的动力放大系数对比

由上述分析可知，当刚度较小时，三自由系统具备明显的三个峰值，与二自由度的二个峰值存在较大的差异。当刚度较大时，尽管两自由度模型和三自由度模型二者曲线走势基本一致，但在频率大小上仍存在一定的差异，这种频率的偏移是由于外框质量以不同程度等效到主系统上引起的系统动力学特性改变所致。因此，选取三自由度动力吸振模型将更符合工程实际。

2 优化与仿真

2.1 参数优化

使用MATLAB的遗传工具箱对上一节中所得到的吸振系统动力放大系数公式中的及进行优化计算，从而得出最优的DVA参数。

由于MATLAB遗传算法工具箱完整地集成了许多函数，其编程的难度[4]可得到了较大的简化。在优化过程中，可通过确定 μ2，μ3，f2与 ζ的值来优化出最优参数 ζ3opt及 f3opt.此处取 μ2=0.1，μ3=0.05，f2=1 或10，ζ3=0.05.首先构建目标函数，本文中的目标函数为式（9）对于自变量g的最大值，优化目标为求解最优ζ3与f3来使得这个最大值最小。遗传算法当中，采用轮盘赌选择方式，遗传代数为40代，变量的维数为2，初代种群的个数为40个。编码方式采用二进制编码，交叉采用交叉率为0.7的单点交叉方式，变异方式则为离散变异。

对于外框刚度较小（f2=1）的情况，将前四个确定参数（其中f2=1）代入遗传算法当中，通过遗传算法 优化 得到 最 优参 数 ζ3opt与 f3opt，结 果 为 ζ3opt=0.316 4，f3opt=0.646 3，min_maxA（g，ζ3，f3）=3.06.

当外框刚度较大（f2=10）时，可得结果为ζ3opt=0.137 4，f3opt=0.897 5，min_maxA（g，ζ3，f3）=4.3156.

遗传算法性能追踪图如图6所示，从图中可以看到该遗传算法所计算出来的最优解具有相当的置信度，将优化出来的数值代入原公式，同时取未经优化的参数数值代入原公式，画出动力放大系数对比图如图7所示，未经优化的动力放大系数曲线图的峰值为 7.314（7.691） 远大于优化之后的 3.06（4.316）。从图中我们不难发现，两种情况下，经过参数优化之后曲线峰值会明显降低，且主要峰值为两个等高峰值。对比传统的二自由度动力吸振放大系数的PQ两点优化定理[5]，此处具有相同的规律，即当一个峰值降低时，另外一个会升高，当峰值相等时，模型为最优解。所以，在此情况下三自由度模型及其优化算法是正确的。

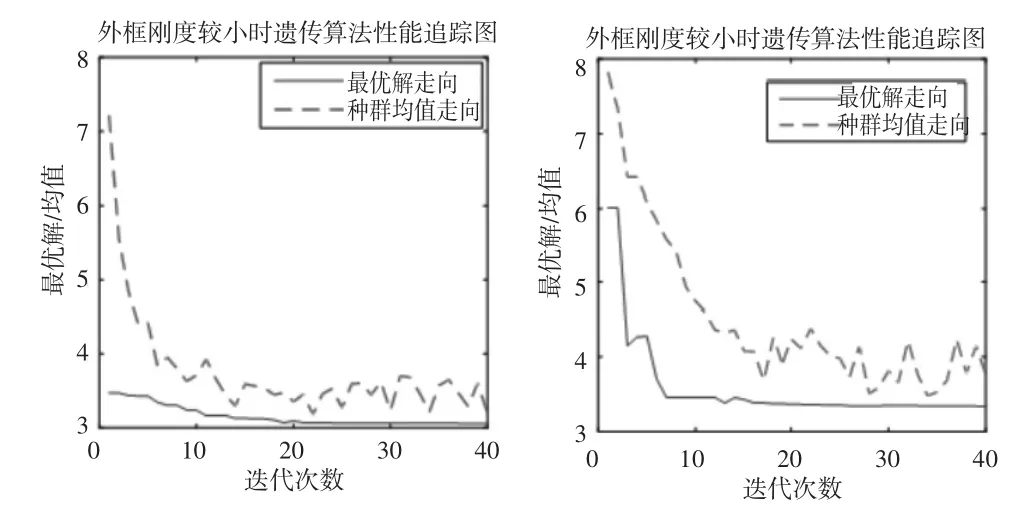
图6 遗传算法性能跟踪图

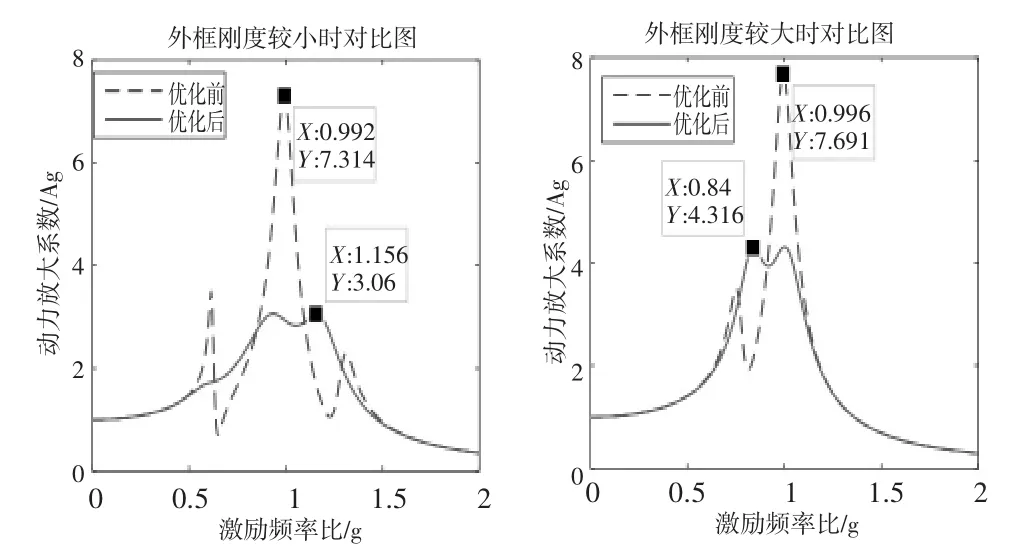
图7 优化前后的吸振特性图

本文优化过程中，只考虑了吸振器的刚度和阻尼，由于论文所采用的是多自由度遗传算法，当需要优化更多的参数时，只需改变程序中的变量维数即可。

2.2 吸振效果的性能仿真

吸振系统参数优化后，其实际吸振效果如何，可利用MATLAB中Simulink模块进行验证。图8为所建立的动力吸振性能Simulink仿真模型图，其外界激励力为正弦信号输入模块，其中主系统响应视窗表示m1的位移波形图。

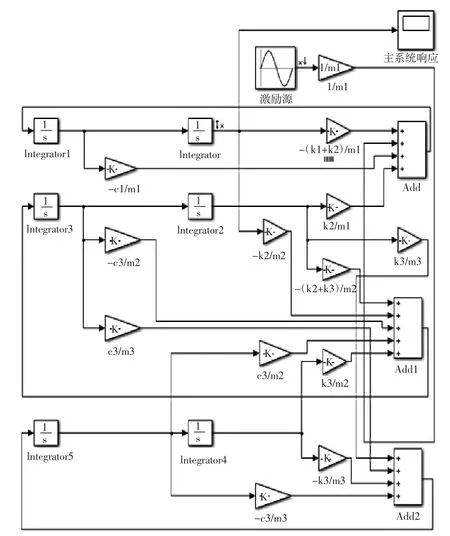
图8 Simulink仿真图

由优化后曲线的分析可知，峰值在g=1左右，本文中列举的参数中主系统固有频率为10 Hz，因此系统对10 Hz左右的激励响应最大。因而若在给定频率为10 Hz的正弦激励信号时系统具备吸振效果，则该三自由度系统动力吸振器具备良好的宽带吸振效果。取与上一节中优化前后相同的参数进行仿真以验证优化前后的效果。加装优化前后动力吸振器的主系统振动曲线如图9所示。图中左边为f2=1时优化前后主系统振动对比图，右边则是在f2=10时优化前后主系统振动对比图。由图对比可知，安装最优参数动力吸振器后的主系统在受到稳态激励力作用时，其振动幅值有明显降低，故而该动力吸振器具备良好的吸振特性，而且，外框刚度值较小时，有利于提高其吸振效果。

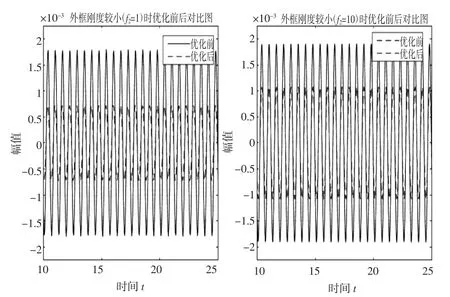
图9 参数优化前后的主系统振动曲线对比

3 结束语

通过本文的研究，可得以下几点结论：

（1）建立了考虑外框质量与刚度参数的三自由度动力吸振模型，推导了其动力放大系数，比较了三自由度系统与传统二自由度系统的差异。

（2）应用遗传算法对三自由度动力吸振系统进行了参数优化，给出了其两个待定参数优化的遗传算法，并列举了优化案例。

（3）通过MATLAB仿真，比较了主系统在DVA安装前后以及DVA参数优化前后的振动特性，其研究结果对利用动力吸振器进行吸振控制具有参考作用。

[1]Shen Y，Chen L，Yang X，et al.Improved design of dynam ic vibration absorber by using the inerter and its application in vehicle suspension[J]，Journal of Sound&Vibration，2015（361）：148-158.

[2]Silva A D G，Jr A A C，Jr V S.Fuzzy Robust Design of Dy namic Vibration Absorbers[J].Shock&Vibration，2016（1）：1-10.

[3]丁文镜.减振理论[M].北京：清华大学出版社，2014.

[4]龚 纯.精通MATLAB最优化计算[M].北京：电子工业出版社，2014.

[5]Ormondroyd，J.and Den Hartog，J.P.，The Theory of the Dynamic Vibration Absorber[J].Trans ASME，1928（50）：7.

Modeling and Optimization of Dynamic Vibration with Considered Parameters of Frame

WANG Jia-xuan1，CAO Yuan-peng2，HUANG Qi-bai1
（1.School of Mechanical Science&Engineering of HUST，Wuhan Hubei 430074，China；2.Hubei Institute of Specialty Vehicle，Suizhou Hubei 441300，China）

Most of the traditional theoretical models of dynamic vibration absorber are two degree of freedom system.However，in engineering application the mass and stiffness of frame may has a certain impact on the system，which makes the dynamic model similar to three degrees of freedom system.In order to prove that，a three degree of freedom model has been established.After that the differences between two degree of freedom and three degree of freedom model was drawn according to a series of comparison.Furthermore，the genetic algorithm toolbox in MATLAB was used to calculate the optimal two parameters of the amplification coefficient formula，which verified that the DVA have a better vibration damping effect under the optimal parameters.

dynamic vibration absorber；three degree of freedom model；amplification formula；genetic algorithm for optimization

TB535.2

A

1672-545X（2017）10-0021-05

2017-07-27

王家璇（1994-），男，湖北仙桃人，硕士研究生，主要研究方向：机械系统动力学，振动与噪声控制。