数学问题解答

2017年4月号问题解答

(解答由问题提供人给出)

2356设a,b,c,d>0，且a+b+c+d=4，求证：

(河南省辉县市一中 贺基军 453600)

证明不失一般性，设a≥b≥c≥d>0，并令

x=b+c,y=a+d=4-x，

首先注意到ad≤a+d-1.①

事实上，由a+b+c+d=4知a≥1且d≤1

⟹(a-1)(d-1)≤0⟹ad≤a+d-1.

这与d>0矛盾.

由①及②知

故

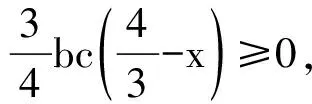
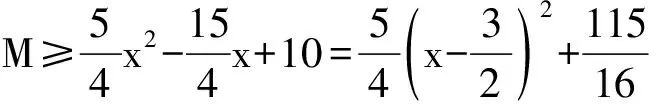
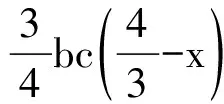
因为x-4=b+c-4<0,

故M≥7.

综上，M≥7，所证不等式成立.

2357在任意△ABC中，求证

cot2A+cot2B+cot2C

(天津水运高级技工学校 黄兆麟300456)

证明显然当△ABC为非钝角三角形时

cotA+cotB+cotC>0，

当△ABC为钝角三角形时,不妨设C为钝角,那么

cotA+cotB+cotC=cotA+cotB-cot(A+B)

故知在任意△ABC中cotA+cotB+cotC恒为正值.

那么由(cotA+cotB+cotC)2

≥3(cotAcotB+cotBcotC+cotCcotA)=3,

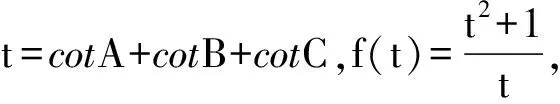
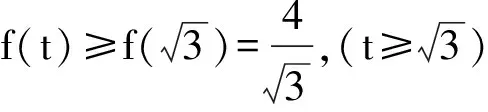
⟹(cotA+cotB+cotC)2

⟹cot2A+cot2B+cot2C+2

⟹cot2A+cot2B+cot2C

以上证明过程中两次用到了恒等式

cotAcotB+cotBcotC+cotCcotA=1.

2358如图，在△ABC中，∠BAC≠90°，点O是其外心，△OBC的外接圆K分别与边AB、AC交

于P、Q，直线OK交BC、圆K分别于M、D，求证：∠PDA=∠PAM.

(陕西省兴平市教研室 吕建恒 713100)

证明设PQ交AD于N，连接DQ，

因为点O是△ABC的外心，OD为圆K的直径，

所以OM⊥BC，BM=CM.

又B、D、O、P四点共圆，

所以 ∠BPD=∠BOD=∠BAC.

所以PD∥AC.

同理可证，QD∥AB.

因此，四边形APDQ是平行四边形.

所以PN=NQ，∠PDA=∠QAN. ①

又B、C、Q、P四点共圆，

所以 ∠AQP=∠ABC.

所以 △AQP∽△ABC.

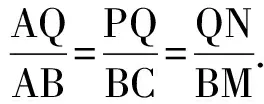
所以 △AQN∽△ABM.

所以 ∠QAN=∠BAM. ②

由①②得 ∠PDA=∠PAM.

2359设△ABC的三边长为a,b,c，外接圆半径为R，内切圆半径为r，旁切圆半径为ra，rb，rc，面积为△，求证：

(河南质量工程职业学院 李永利 467000)

证明设△ABC的半周长为p，则

且a+b+c=2p，

ab+bc+ca=p2+4Rr+r2，

于是

+(p-c)(p-a)]

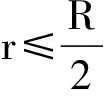
2360n是非负整数，记Fn=22n+1，这称为Fermat数. 对于给定的m∈N+，求能整除2m+1的所有不同的Fermat数.

(浙江温州市区马鞍池东路1-408 陈克瀛 325000)

(ii)r>k. 用反证法. 若Fr| 2m+1，则Fr| (2m+1) (2m-1)，即Fr|22k+1·l-1，又显见Fr|22r+1-1，根据GCD的性质得到

Fr|(22k+1·l-1，22r+1-1).

(1)

(2)

但r>k⟹r≥k+1⟹22r+1>22k+1-1，这与(2)矛盾！

综合以上各点得，给定正整数m=2k·l，2m+1 的互异的Fermat数因子只有Fk这一个.

2017年5月号问题

(来稿请注明出处——编者)

2361若x,y,z是正实数，求证：

(1)

其中“∑”表示轮换对称和.

(四川成都金牛西林巷18号华鑫园A601宿晓阳 610031)

2362在△ABC中，a,b,c为其三边长，ra,rb,rc与ha,hb,hc是其对应三边上的旁切圆半径与高，则有

(hb+hc)(hc+ha)(ha+hb)

(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000)

2363在ABC中，AD、BE、CF相交于一点O，点D、E、F分别在△ABC三边BC、CA、AB上，则有

min(AD,BE,CF)

≤OD+OE+OF≤max(AD,BE,CF)

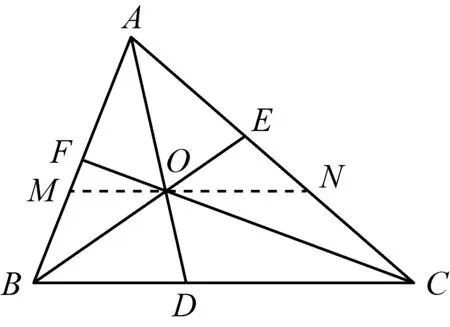
(西安卫星测控中心 赵晓辉 714000)

2364给定m≥3且m∈N，设a1,a2, …,am>0，n≥m且n∈N，求证：

(湖南师大附中数学教研组 张湘君 410006)

2365已知，(如图)在△ABC中，点P、Q分别在CB、BC的延长线上，AE垂直于∠ACQ的平分线于点E，BD1、BD2在∠ABP的内部，且∠ABD1=∠PBD2，AD1⊥BD1，AD2⊥BD2，直线D1E、D2E分别与直线PQ交于点H、G.

求证：△EGH为等腰三角形.