中学数学教师认识信念系统的教龄差异研究

谢圣英



中学数学教师认识信念系统的教龄差异研究

谢圣英

（湖南师范大学 数学与计算机科学学院 高性能计算与随机信息处理省部共建教育部重点实验室，湖南 长沙 410081）

了解中学数学教师的认识信念系统的教龄差异，有利于为教师专业成长提供建设性建议．采用有较高信效度的自编“中学数学教师认识信念系统量表”，对171名在职中学数学教师的认识信念系统进行了考察．结果发现：老教师与新手教师对数学学习的本质、方式、速度以及影响数学学习的因素方面的认识信念存在显著性差异；随着教龄增长，教师的认识信念系统的进步倾向是先上升后下降的趋势；其中，在关于数学学习、数学教学、学生以及教师自身的认识信念维度，教龄为6—10年的教师群体比其他任何教龄段教师群体都要更倾向于建构主义、民主和积极的认识信念．

数学教师；观念；认识信念系统；认识信念系统量表；教龄差异

1 问题提出

认识信念是个体对知识以及知识认知过程的直觉认识，它涉及对知识性质、知识认知、学习性质、学习条件、环境条件等维度的认识．认识信念系统由知识信念、认知方式信念、学习信念、文化信念、行为表现和自我调节信念组成，这些要素之间相互联系、相互作用而形成一个复杂的结构[1]．

早期的研究发现，数学教师的信念会影响他们使用教学策略的类型．数学教学中强调速度、准确和对规则记忆的策略同教师的“学习是快速的”，“仅仅有一个正确答案”，“成功需要天生的能力”，“数学知识是不变的而且包含很多孤立的信息”，“教师是维护数学知识的权威”等信念是联系在一起的[2]．拥有成熟认识信念的教师可能在课堂上更多地解决结构不良问题并强调反思，而与之相反的则是突出基本技能和传输核心概念和事实；拥有成熟认识信念的教师更可能注重使用策略来将知识建立个人意义，并将那些与重要知识有联系的思想系统化．“教师的信念为我们理解他们的专业发展和改变提供了一扇重要的窗口——不仅对于教师未来行为预测，而且更为重要的是可以洞悉教师变革的过程并为未来的专业发展活动提供信息．”[3]总之，教师关于数学教学的认识信念，决定着教师的教学决策和行为，也间接影响着学生的学业成绩和学习态度．教师认识信念研究的重要意义在于如何为教师专业发展提供建设性的建议．那么，中学数学教师的认识信念系统的发展究竟随着教龄的增长会有什么样的变化？新手教师和老教师的认识信念有否不同差异？这些结果对于数学教学实践中，新手教师和老教师互动交流、数学教师专业发展水平提升有何启示呢？

研究将立足于了解中学数学教师持有的认识信念系统，比较不同教龄教师群体的认识信念的主要内容和结构，从而探索数学教师认识信念发展的可能路径．这对于未来的中学数学教师教育、教师观念转变以及数学新课程的实施等都具有一定的参考价值．具体而言，应用“中学数学教师认识信念系统量表”对中学数学教师的认识信念系统进行测量，利用检验、方差分析等统计方法分析中学数学教师在教龄变量上是否存在差异，考察教龄对数学教师认识信念系统的影响．

2 主要研究假设

假设：教师的认识信念系统存在显著的教龄差异．

3 研究方法

3.1 被试选择

湖南和江苏两省共计202名中学数学教师参与调查．最终收回数学教师认识信念系统、教学监控能力和人口学3个量表均有效的量表为171份，量表回收有效率为84.65%．

3.2 研究工具与统计方法

采用自编“中学数学教师认识信念系统量表”[4]．该量表采用里克特四点量表（Likert Scale）形式，共计26个项目，包括关于数学知识的认识信念（5个项目）、关于数学学习的认识信念（5个项目）、关于数学教学的认识信念（9个项目）、关于学生的认识信念（3个项目）和关于教师自身的认识信念（4个项目）．各项目在编拟之前，先制定了统一的理论维度表．量表的各项信效度指标基本达到测量学要求，是可靠的测量工具．各维度的内部一致性系数在0.556~0.850之间，总量表内部一致性系数为0.874．维度与量表的整体概念一致并且具有独立的结构内涵；同时，采用结构方程模型（SEM）技术进行验证性因素分析，结果也表明“中学数学教师认识信念系统量表”具有很好的结构效度．使用SPSS11.0进行数据处理，统计方法主要采用描述性统计、独立样本检验、单因素方差分析以及统计图形．

4 研究过程及结果

4.1 中学数学教师认识信念系统的总体状况

171名中学数学教师认识信念系统总分及分量表得分的描述性统计结果见表1．样本中学数学教师的认识信念系统总均分为74.388±8.797，其中最低分为48，最高分为96．关于学生的认识信念系统层面单题平均分最高，从高到低依次为：关于教师自身的认识信念、关于数学知识的认识信念、关于数学教学的认识信念，关于数学学习的认识信念层面单题平均分最低．

表1 中学数学教师认识信念系统描述性统计量（N=171）

根据中学数学教师认识信念系统的理论构想，分5个维度考察了中学数学教师的日常教学工作所涉及的认识信念的主要内容．研究发现各维度和总量表单题平均分均在2.5分以上．其中，关于学生和教师自身的认识信念维度单题平均分达到3.0分以上．这表明样本教师的认识信念系统整体倾向于发展的、相对的，尤其是关于学生和教师自身的认识信念．

4.2 中学数学教师认识信念系统的教龄差异分析

不同教龄段的中学数学教师在认识信念系统量表各分量表和总量表得分的描述性统计结果见表2．

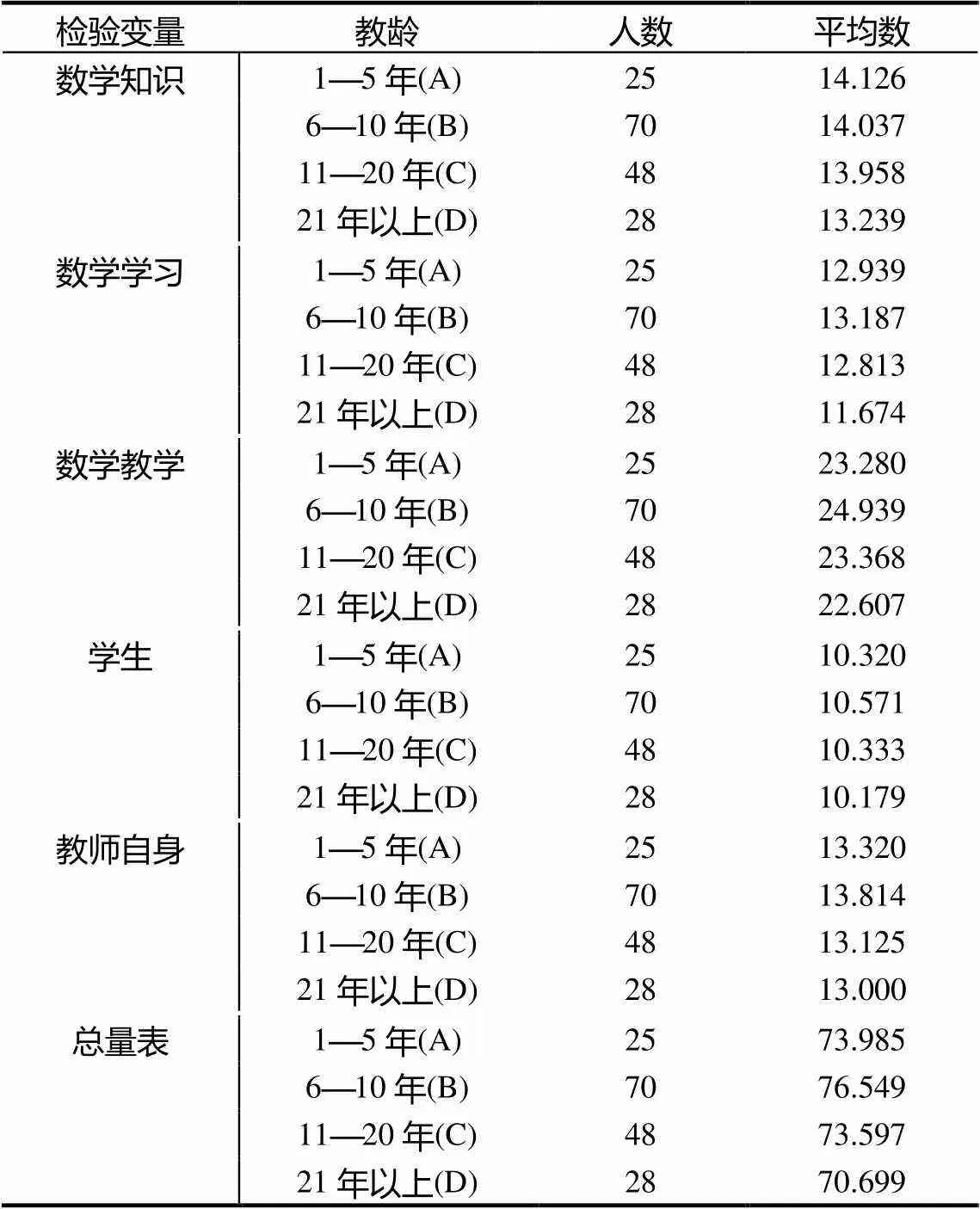
表2 不同教龄中学数学教师认识信念系统的描述性统计量

采用单因素方差分析（One-Way ANOVA）方法检验中学数学教师在认识信念系统及其各分量表上的得分是否存在教龄差异，结果显示不同教龄的中学数学教师在认识信念系统总量表（(3, 167)=3.328，<0.05）以及关于数学学习（(3, 167)=3.193，<0.05）、数学教学（(3, 167)=2.753，<0.05）的认识信念系统分量表层面存在显著差异．

接着采用最小显著差异法（Least Significant Difference， LSD）进行事后比较，寻找差异产生的根源．结果表明：①认识信念系统总量表的所有得分中，教龄在“21年以上”的中学数学教师（D）分数最低，且显著低于“6—10年”组群体（p<0.05）．②关于数学学习的认识信念层面，“21年以上”教龄的教师得分均显著低于其他各年龄段的数学教师（p<0.05）．③关于数学教学的认识信念层面，“6—10年”教龄的数学教师得分显著高于“11—21年”及“21年以上”教龄的教师（p<0.05）．

图1为不同教龄中学数学教师认识信念系统的单题平均数．总体看，教师的认识信念系统的得分是先上升后下降的趋势（见图1中粗黑线）．教龄“21年以上”的中学数学教师在认识信念系统总量表及各分量表的单题平均分低于其他教龄组群．除了关于数学知识的认识信念维度，教龄为6—10年的教师在认识信念系统的其它4个维度比其他教龄段教师的平均分都要高．但是，关于数学知识的认识信念维度，在6—10年处没有出现类似峰值，整体变化相对也比较小．

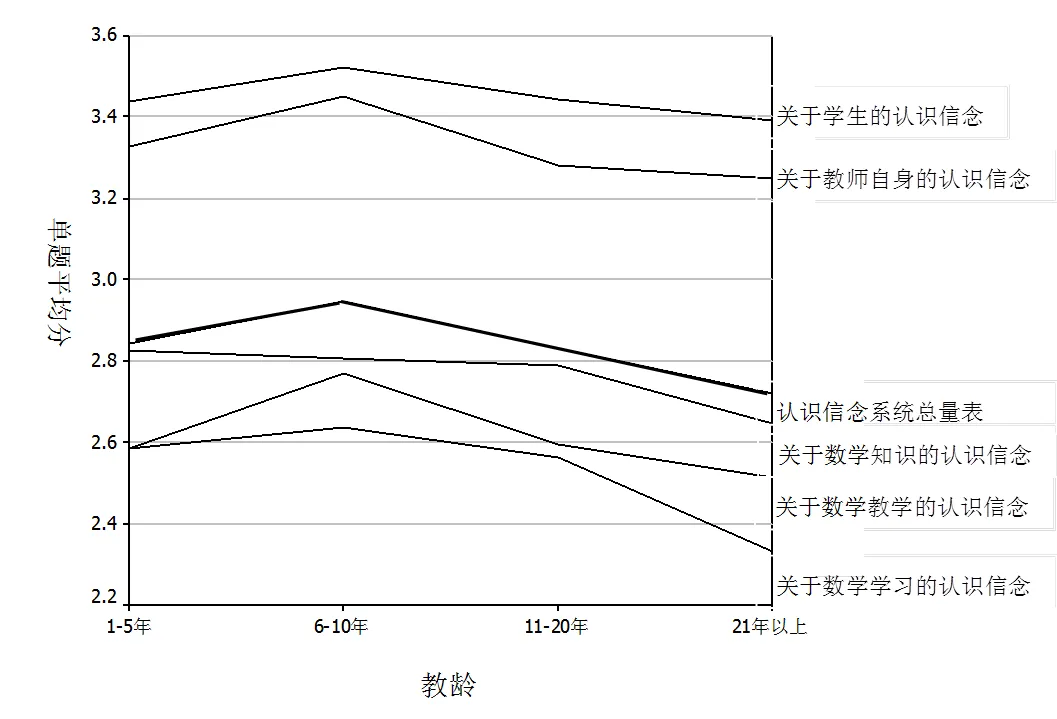
图1 不同教龄中学数学教师认识信念系统的单题平均数

4.3 新手教师—老教师认识信念的差异比较

《现代汉语词典》中“新手”是“刚从事某种工作尚未熟练的人”；“老手”是“对于某种事情富有经验的人”．因此，“新手教师”是指刚参加工作没多久的年轻教师；“老教师”则是富有教学经验的教师．相对于“老教师”，对“新手教师”的界定比较统一．“新手教师”主要是指参加工作1—2年的教师或进行教育实习的毕业生，还有一些学者把教龄为0—4年的教师界定为新手教师[5]．研究中将取被试中教龄处于两极的样本分别作为新手教师（教龄1—5年）和老教师（教龄在21年以上）进行认识信念系统方面的比较．

从171份认识信念系统有效数据中选取新手教师25人、老教师28人进行认识信念系统差异的检验（表3）．结果发现，新手教师在认识信念系统总量表及其5个分维度的平均分都高于老教师，且新手教师在“关于数学学习的认识信念”维度的得分显著高于老教师（=2.225，＜0.05）．此时，“关于数学学习的认识信念”维度差异的实际效应量为中等（=0.611），这表明新手教师和老教师的认识信念存在差异，而且在“关于数学学习的认识信念”维度存在显著性差异．

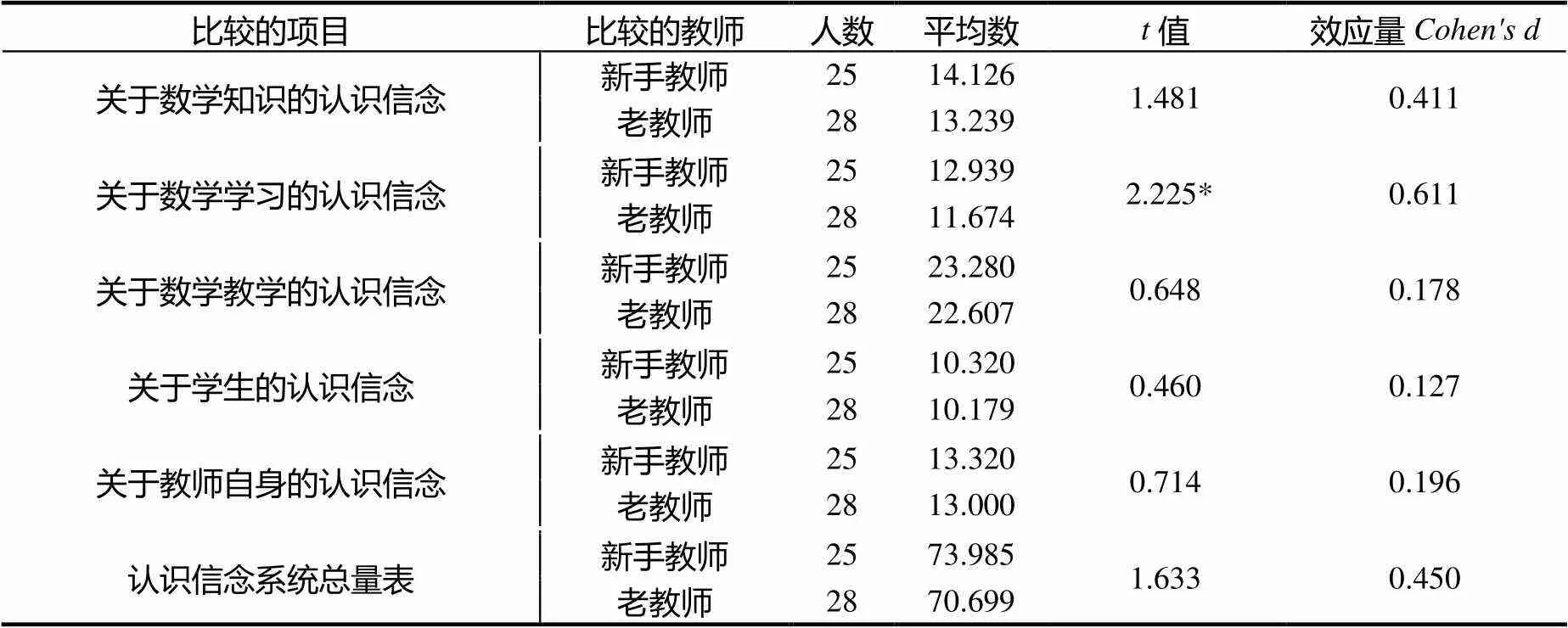
表3 新手教师和老教师的认识信念系统平均分的t检验

注：﹡＜0.05

无论是新手教师还是老教师，他们的认识信念系统都呈现出较为清晰的两个部分．其中一个部分是关于数学知识、数学学习以及数学教学的认识信念，这3个维度的单题平均分相对更高而且更为接近，而另一个部分是关于学生和教师自身的认识信念，这两个维度的单题平均分接近．总体看来，从新手教师与老教师，认识信念系统内部各维度单题平均分的变化呈现出差异增大的态势．

5 讨论

5.1 认识信念系统的总体水平

研究结果为中学数学教师的认识信念系统的各层面及总量表的单题平均分均高于2.5分．这表明中学数学教师的认识信念系统在取向上没有不同，均倾向于进步取向，只是倾向程度不同而已（见表1）．从认识信念系统的各维度来看，中学数学教师关于学生和教师自身的认识信念相对更加倾向于认同个体差异、积极、民主和乐观（平均分高于3.0分）．该结果与之前一些相关的研究结论比较一致，如丁福全对安徽无为县192名中学数学教师的教学信念（包括数学本质、数学学习、数学教学和数学评价4个方面）进行了调查分析，研究结果表明中学数学教师的教学信念总体倾向于进步取向[6]；周兆透用数学信念及课堂教学问卷调查了中国10所师范院校的数学教师，发现虽然在某些问题上表现出有互相矛盾的信念，但他们大多已拥有了比较新的数学信念和教学理念，包含了较多的建构主义成分[7]．

5.2 新手教师和老教师认识信念系统的差异

将样本中教龄为1—5年的教师作为新手教师，将教龄在21年及以上的教师作为老教师．研究结果显示新手教师和老教师在关于数学学习的认识信念维度存在显著差异．具体地，新手教师对数学学习的本质、方式、速度以及影响数学学习的因素方面的认识信念更加倾向进步．在认识信念系统的其它4个维度（关于数学知识、数学教学、学生以及教师自身的认识信念），新手教师也比老教师的得分高，只是两组之间的差异没有达到统计学上的显著水平．总之，整体上看，新手教师的认识信念系统更为进步，尤其是关于数学学习的认识信念，但新手教师与老教师两组群体间认识信念系统的差异不显著．有研究者也发现初中数学教师教学观、学习观和数学观的水平不会因为教龄的自然增长而有显著性差异[8]．但丁福全（2008）发现11—20年教龄的中学数学教师关于“数学学习”的信念显著优于教龄5年以下的新手教师，而两者在关于数学本质、数学学习、数学教学和数学评价方面的信念均不存在显著差异[6]．该研究与丁福全的研究均表明在关于数学学习的认识信念维度，不同教龄的数学教师存在显著差异，但是出现显著性差异的教龄段以及哪一组教师的“数学学习”信念倾向性最明显，两项研究的结果不完全一致．

5.3 认识信念系统随教龄增长的变化

不同教龄段教师的认识信念系统存在显著差异（表2），而且差异主要体现在总体的认识信念以及关于数学学习和数学教学的认识信念维度．整体来看，随着教龄的增长，教师的认识信念系统的得分是先上升后下降的趋势（图1）．其中，在关于数学学习、数学教学、学生以及教师自身的认识信念维度，教龄为6—10年的教师群体比其他任何教龄段教师群体都要得分高，体现了该群体整体对于数学教与学、学生和自身持有更加建构主义、民主和积极的认识信念．吴卫东和骆伯巍曾根据培训实践，按发展水平的差异以及职业年龄特征把教师群体分为新手型教师（0—5年）、适应型教师（5—10年）、成熟型教师（10—20年）和专家型教师（20年以上）[9]．吴卫东和骆伯巍研究发现，新手教师所具有的知识多数来源于间接的书本知识，主要是教师职前教育中所接收的学科知识与教育学、心理学知识，他们对这些陈述性知识的把握是表面的、抽象的，缺乏具体实例的支撑．对解决“怎么办”的程序性知识的把握，即教学技能，包括导入、语言、板书、讲解、提问、演示、变化、强化、练习指导、组织、结束等具体技能，往往停留在前结构水平上，无论是对教学技能的系统认知，还是对教学技能的有意识调用水平都比较低．适应性教师的知识结构中程序性知识已经比较丰富，具体表现在他们已掌握基本的教学技能，并能熟练地在熟悉的教学环境中运用，但这种运用多为长期练习的结果，条件反射的成分较大．因此，新手教师参与教学有较高的积极性，由于缺少丰富的教学经验，为了上好课，他们需要花费不少的时间和精力．也因为仍然处于教学的摸索过程和积累阶段，他们没有更多的心思用来接受和仔细消化新的教学理念．但是，经过一段时间的锻炼，新手教师成长起来了，他们开始更多地思考和学习新的教学理念．同时，他们尚未出现成熟型教师专业成长过程中的“高原期”，对新事物也有较大的兴趣和较高的接受度，于是就表现为认识信念系统比较“潮流”．这其实也是教龄为6—10年的教师在关于数学学习、数学教学、学生以及教师自身的认识信念比其他任何教龄段教师都要先进的主要原因．

需要特别指出的是，教师关于数学知识的认识信念维度水平比较稳定，在教龄为6—10年处没有出现类似峰值，整体变化相对也比较小．王晓明对教师数学观的调查内容也包含对数学知识的来源、确定性、发展和价值等的观念和认识，这与研究中关于数学知识的认识信念分量表测量内容较为一致，而且两研究结论也颇为相似．他对长春市初中数学教师的信念进行调查研究，发现教龄为8—10年的教师在关于数学教学、数学学习、数学观两方面信念得分比教龄为7年以下和11年以上的教师都高．但是，教师的数学观趋于稳定，与其它两个维度不同，较少受其它因素的影响．王晓明还发现，教龄在11年以上教师的数学观则比所有教龄段的教师都低，而他们的教学观和学习观平均分均低于8—10年的教师，却高于或等于教龄为7年以下的教师[8]．教龄“21年以上”的中学数学教师关于数学学习的认识信念水平显著低于其他3个教龄段的教师．在关于数学教学的认识信念维度，教龄21年以上的教师仍然显著落后于教龄为6—10年的教师．这里的研究与王晓明研究结果的不同之处在于，他认为不同教龄教师的数学观、学习观和教学观不存在统计学上的显著差异，而这里的研究则发现了不同教龄间教师认识信念系统的显著差异．类似地，程德胜和喻平研究也发现，6—10年与11—21年教师的认识信念倾向性与该群体教师处于专业发展的成熟期、高峰期有相关性．教龄21年以上教师，数学认识信念与教龄有一定关系[10]．此外，尚晓青等比较中美数学职前教师教育的发现：中国职前数学教师教育对于理论知识的重视程度远远大于实践知识，关于“深厚的数学知识”和“广泛的科学知识”两类知识分别位于前两位；而对于“关于学生的知识”，中国这项数据排在末位[11]．这也从某种程度上解释了为什么教师关于数学知识的认识信念维度水平比较稳定，而关于数学学习、数学教学、学生以及教师自身的认识信念存在较大差异的原因．

5.4 对数学教师文化及专业成长的启示

数学教师认识信念教龄差异研究的重要性在于其可为教师文化和教师专业成长提供一些实证支持和启示．一方面，教师认识信念系统上的异同可以认为是导致不同教师文化形式并存的内在原因之一．Hargreaves（1992）曾经分析了4种教师文化形式，即个人主义文化（Individualistic Culture）、分化的文化（Balkanized Culture）、合作的文化（Cooperative Culture）和硬造的合作（Contrived Collegiality）[12]．教师认识信念系统上的差异可以帮助人们深入理解这些不同的教师文化．另一方面，数学教师认识信念系统上的教龄差异研究结果，对于引导不同教龄教师之间的有效合作交流，对于数学教师专业成长也非常重要．Staton和Hunt（1992）就发现经验型教师对于新手型教师的帮助有显著性作用[13]．所以，需要对新手型教师，特别是6年以内的数学教师，加强实践指导，让“以老带新”、“传、帮、带”的传统制度化；而6—10年的数学教师更倾向于接受新的事物和新的教学理念，此时期的数学教师进行培训学习，可能收效最佳．此外，也需要创造机会让经验型教师与其他教师互动交流，让他们走出相对保守的认识信念系统，尝试接受新的教育教学思想，突破专业发展的瓶颈期，为成长为专家型教师扫清障碍．因为教师思想观念是教学行为的先导，数学教师对新课程教学理念主观上的认同与肯定特别重要，它是教师教学行为优化与完善的最为基础的条件与产生行动的动力，它已经为数学教育改革创造出了良好的氛围[14-17]．

6 小结

6.1 中学数学教师的认识信念总体水平倾向于进步取向

中学数学教师的认识信念系统总体倾向于进步取向，只是倾向程度不同而已．其中，中学数学教师关于学生和教师自身的认识信念相对更加成熟．

6.2 新手教师与老教师的认识信念系统存在显著差异

新手教师和老教师在关于数学学习的认识信念维度存在显著差异．新手教师对数学学习的本质、方式、速度以及影响数学学习的因素方面的认识信念更加倾向于个人建构、自主发现和动机作用等．在认识信念系统的其它4个维度，新手教师也比老教师的得分高，但是两组之间的差异没有达到统计上的显著水平．

6.3 认识信念系统随教龄增长而变化

不同教龄间教师认识信念系统的显著差异．随着教龄的增长，教师的认识信念系统的“先进性”是先上升后下降的趋势．其中，在关于数学学习、数学教学、学生以及教师自身的认识信念维度，教龄为6—10年的教师群体比其他任何教龄段教师群体都要“潮流”．但是，教师关于数学知识的认识信念维度的水平比较稳定，在教龄为6—10年处没有出现类似峰值，整体变化相对也比较小．

由于受研究时间和精力所限，研究所收集的数据主要来自湖南和江苏两省的一线中学数学教师．该结果是否能够推广到全国，还有待进一步研究．另外，研究采用Likert量表让被试自我报告，测量的方式虽然简单，但有可能高估或低估，而不易获得准确的数据信息．如同所有量化研究一样存在着一些限制，比如，在问题回答中，被试可能因为受到环境和心理等因素的影响而未能准确真实地反映自己的想法，因而研究的结论可能受到一定程度的影响．因此，今后还需进一步配合访谈和课堂观察等质化研究方法进行研究．此外，尽管对不同教龄的数学教师作了横断面研究，并由此得出了一些关于教师认识信念系统发展的结论．但是从某一特定时间内不同样本的发展来做出的推断存在一定的风险，而且因果推断不足．所以还需要做长期的跟踪研究更能深入细致地回答数学教师认识信念系统的发展问题．

[1] SCHOMMER M. Explaining the epistemological belief system: introducing the embedded systemic model and coordinated research approach [J]. Educational Psychologist, 2004, 39(1): 19-29.

[2] MUIS K R. Personal epistemology and mathematics: a critical review and synthesis of research [J]. Review of Educational Research, 2004, 74(3): 317-377.

[3] HART L C. A four year follow-up study of teachers’ beliefs after participating in a teacher enhancement project [M] // LEDER G C, PEHKONEN E, TÖRNER G. Beliefs: a hidden variable in mathematics education. Dordrecht: Springer, 2002: 161-176.

[4] 谢圣英．中学数学教师认识信念系统量表的编制与信效度检验[J]．数学教育学报，2014，23（4）：47-54．

[5] 连榕．新手—熟手—专家型教师心理特征的比较[J]．心理学报，2004，36（1）：44-52．

[6] 丁福全．中学数学教学信念与教学行为的相关研究[D]．桂林：广西师范大学，2008：39-48．

[7] 周兆透．关于高师院校数学教师的信念的调查研究[D]．上海：华东师范大学，2001：29-34．

[8] 王晓明．初中数学教师的教师信念的研究[D]．长春：东北师范大学，2009：35-38．

[9] 吴卫东，骆伯巍．教师的反思能力结构及其培养研究[J]．教育评论，2001（1）：33-35．

[10] 程德胜，喻平．高职校数学教师认识信念的维度分析与倾向性研究[J]．数学教育学报，2015，24（2）：91-97．

[11] 尚晓青，FARRELLA，陈晓端，等．中美职前数学教师理想知识的比较研究——基于培养方案的分析[J]．数学教育学报，2015，24（4）：13-18．

[12]  HARGREAVES A. Cultures of teaching and educational change [C] // BIDDLE B J, GOOD T L, GOODSON I F. International handbook of teachers and teaching. Dordrecht: Springer, 1997: 1 297-1 319.

[13]  STATON A Q, HUNT S L. Teacher socialization: review and conceptualization [J]. Communication Education, 1992, 41(2): 109-137.

[14] 张昆，曹一鸣．完善数学教师教学行为的实现途径[J]．数学教育学报，2015，24（1）：33-37．

[15] 程晓亮，刘影，付军．基于一体化思想的卓越中学数学教师培养模式[J]．数学教育学报，2017，26（3）：88-90．

[16] 杨鹏，胡志奇，尹彦红．数学教师素质结构的实证研究[J]．数学教育学报，2017，26（3）：91-93．

[17] 郑毓信．“问题意识”与数学教师的专业成长[J]．数学教育学报，2017，26（5）：1-5．

[责任编校：周学智]

Study on Teaching Year Deference of High School Mathematics Teachers about Their Epistemological Beliefs System

XIE Sheng-ying

(Key Laboratory of High Performance Computing and Stochastic Information Processing (HPCSIP) (Ministry of Education of China), College of Mathematics and Computing Science, Hunan Normal University, Hunan Changsha 410081, China)

The purpose of this study was to investigate current situation and developmental characteristics of high school teachers’ epistemological beliefs system, aiming to benefit our improving mathematics teachers’ professional development in a targeted manner. The study, using the self-complied High School Mathematics Teachers’ Epistemological Beliefs System Scale with high credibility and validity, had observed 171 mathematics teachers’ epistemological beliefs system. The results showed that there was significant difference between novice teachers and veteran teachers in their epistemological belief about mathematics learning. Comparatively, the novice teachers had got more sophisticated beliefs about the nature, way, speed, and impact factors of mathematics learning. There were significant differences exsit among different teaching-year groups: with the growth of seniority, teachers’ epistemological beliefs’ maturity was first increasing and then decreasing. Those who had 6-10 years teaching experience possess the most sophisticated epistemological beliefs, especially in the mathematics learning, mathematics teaching, students and teacher themselves dimensions.

mathematics teacher; beliefs; epistemological beliefs system; epistemological beliefs system scales; difference in years of teaching experience

G451.2

A

1004–9894（2017）06–0067–05

谢圣英．中学数学教师认识信念系统的教龄差异研究[J]．数学教育学报，2017，26（6）：67-71．

2017–10–30

2014年度湖南省哲学社会科学青年基金项目——中学数学教师认识信念系统及其发展研究（14YBA280）；湖南省重点学科建设项目

谢圣英（1981—），女，湖南华容人，副教授，博士，主要从事课程与教学理论及数学学科教学论研究．