美国早期教科书中的无理数概念
2017-12-22栗小妮汪晓勤
栗小妮,汪晓勤
美国早期教科书中的无理数概念
栗小妮,汪晓勤
(华东师范大学 教师教育学院,上海 200062)
1820—1969年出版的100种美国中学和大学代数教科书先后给出了8种不同的无理数的定义,20世纪20年代开始,才出现用“无限不循环小数”定义无理数.早期教科书中无理数概念的演变为今天的教科书编写和无理数概念教学,提供借鉴.教科书编写应体现无理数定义的多样化,并体现无理数是不能用整数和分数表示的数.可借鉴无理数定义的发展历史,运用重构历史的方式设计无理数概念教学,促进学生对无理数以及实数体系的整体理解和掌握.
无理数;无理式;不尽根;定义
1 引言
古希腊毕达哥拉斯学派认为“万物皆数”,把数归结为整数或整数比,在几何上这相当于说:对于任意给定的两条线段,总能找到某第三条线段,作为公共度量单位.但后来发现,存在不可公度的线段(如正方形的对角线与其一边),它们的长度之比就是后人所称的无理数,由此引发了史上第一次数学危机.但不少数学家一开始并不接受无理数,无理数理论经历了缓慢而艰辛的发展过程,直到两千三百多年后的19世纪末才出现了无理数的严格定义和完善的理论.
现行教科书将有理数定义为“整数和分数”,而采用“无限不循环小数”来定义无理数,与之前的有理数定义并无关联,且完全脱离了它最原始的来源.学生常常会问,这里的“有”、“无”和“整数和分数”、“无限不循环小数”之间有什么关系?“无理数真的没有道理吗?为什么称为无理数?”初中学生接触的无理数通常有3类:不尽根、π和构造的无限不循环小数.通过一定课时的学习和周而复始的练习,大多数学生能够从形式上判断什么样的数是无理数,但学生并不理解到底什么是无限不循环小数?为什么无理数是无限不循环小数?已有研究表明,学生对无理数既“不能用整数和分数表示”同时也是“无限不循环小数”的理解存在障碍,对于无限不循环小数是无理数存在疑惑,常常忽视无限不循环小数的结构特征[1].60%的初中生对无理数的无限不循环性缺乏坚定的信念,反映出学生对无理数概念的理解存在问题[2].在一项对职前数学教师的调查中发现,虽然职前数学教师在高中和大学已经接触过许多其它形式的无理数,但他们对无理数的印象依然停留在“小数型”和“根号型”,且对这两种形式的掌握也不尽理想,没有对无理数的概念形成整体性的理解[3].
由此可见,用“无限不循环小数”定义无理数,脱离了学生先前所学的有理数知识,无理数定义与有理数定义相分离,不利于学生对实数体系的整体理解和掌握.美国数学史家卡约黎(F. Cajori,1859—1930)认为,“学生所遭遇的困难往往是相关学科的创建者经过长期思索和探讨后所克服的实际困难”[4];另一位美国数学史家史密斯(D. E. Smith,1860—1944)认为:“困扰世界的东西也会困扰儿童,世界克服其困难的方式提示我们,儿童在其发展过程中会以类似的方式来克服类似的困难.”[5]因此,了解前人对无理数的理解,对于认识今日学生的认知困难具有重要借鉴意义.
通过对1820—1969一百五十年间出版的100种美国代数教科书中有关无理数内容的考察,试图回答以下问题:早期代数教科书如何定义无理数?定义如何演变?对今日教科书编写和课堂教学有何启示?
2 研究对象
共选取20世纪70年代之前出版的100种美国代数教科书,若以十年为一段,则各教科书的时间分布情况如图1所示.
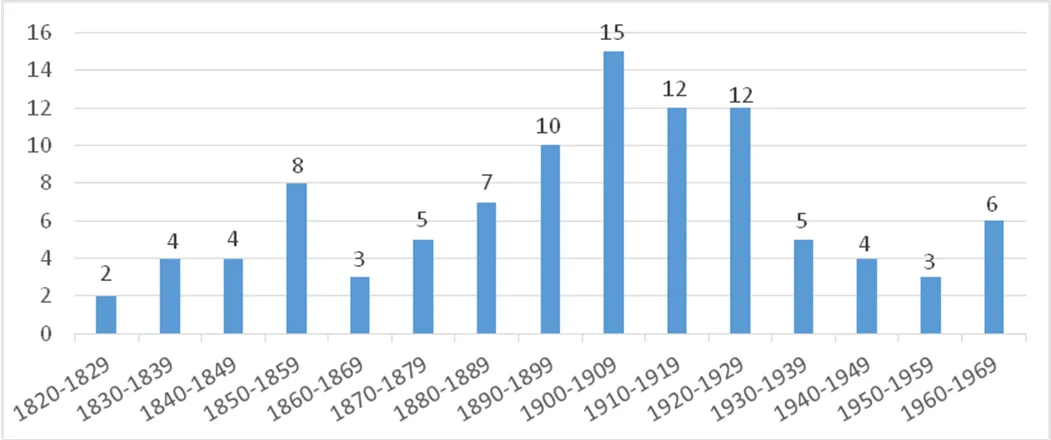
图1 100种教科书的时间分布
其中,对于同一作者再版的教科书,若内容无变化,则选择最早的版本,若内容有变化,则将其视为不同教科书.
100种代数教科书中,61种是中学教科书,39种是大学教科书.无理数的定义所在章节大致可以分为“根式”、“定义与公理”、“数”、“因式分解”、“数的运算”5类,如表1所示.其中无理数定义最多出现在“根式”章节,占64%;其次是“数”,占20%.

表1 无理数概念在100种代数教科书中的章节分布
以30年为一个时间段,图2给出的是“根式”和“数”章节在每个时间段的分布,反映出早期人们对无理数类型的认识主要局限于“根号型”,在20世纪50年代后的教科书中,无理数定义均出现在“数”这一章节中,且实数均单独列为一章.
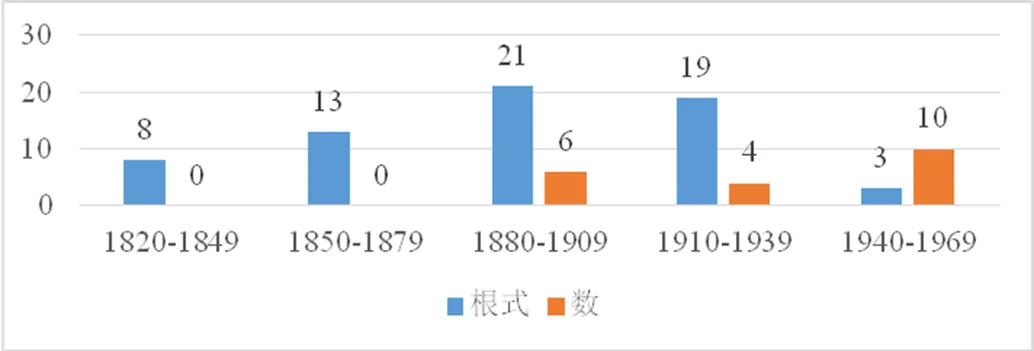
图2 “根式”和“数”章节时间分布
3 无理数定义的分类
由于完整的实数理论体系直到19世纪末才建立,在100种教科书中,绝大多数并没有把无理数或者实数单独列为一章,而是将其与“式”的研究放在一起.所以,这里涉及3种有关无理数的术语.
(1)无理数(irrational numbers).为实数中的一类,与现代教科书中所指相同.如:Young & Jackson(1910)给出的定义是:“任何不是有理数的数称为无理数.”

(3)无理式(irrational expression),在20世纪初,实数理论体系形成后,部分代数教科书开始将无理式与无理数分开定义,数与式分别独立成章.如Milne(1902)给出的定义是:“若一个式子必须使用根号来表达,则称之为无理式;若一个数不能用分数或整数来表达,则称之为无理数.”
综上,将100种教科书中的无理数定义分为两大类:“区分数与式的定义”、“不区分数与式的定义”.若定义之后没有具体例子说明是无理数还是无理式,则统一将其归为“不区分数与式的定义”一类.以30年为分布单位,图3是两类定义的具体时间分布.从图3中可见,随着19世纪末实数理论体系的建立,“不区分数与式的定义”逐渐退出历史舞台,数与式逐渐分离,成为初等代数的两个不同对象.
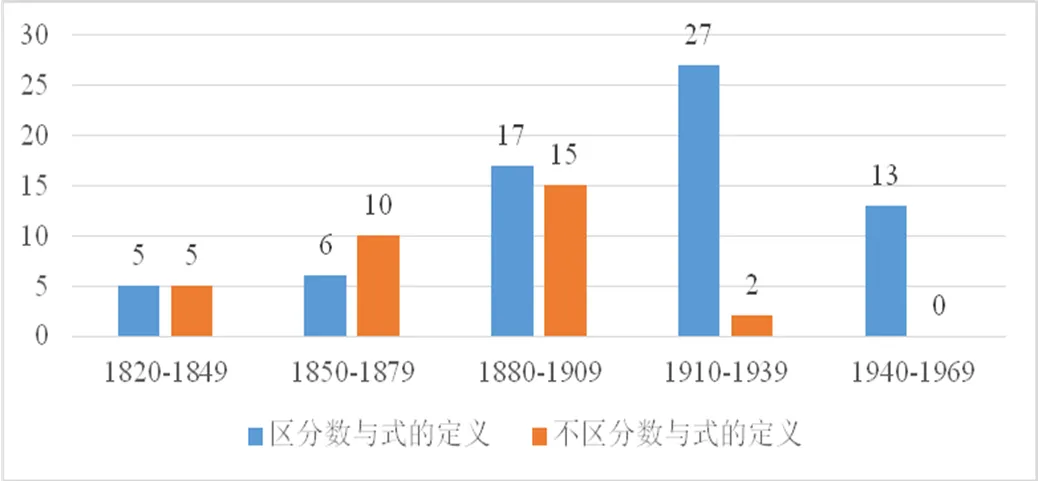
图3 两类定义的时间分布
3.1 区分数与式的定义
100种教科书共计给出了100种定义,区分无理数和无理式的共68种,占68%.根据详尽的统计和分析,这些定义又可以分为“表示定义”、“数值定义”、“形式定义”、“反向定义”、“分割定义”、“几何定义”、“混合定义”、“小数定义”共8类.这8类在68种定义中的分布如图4所示.其中,“表示定义”和“形式定义”所占比例相对较高.
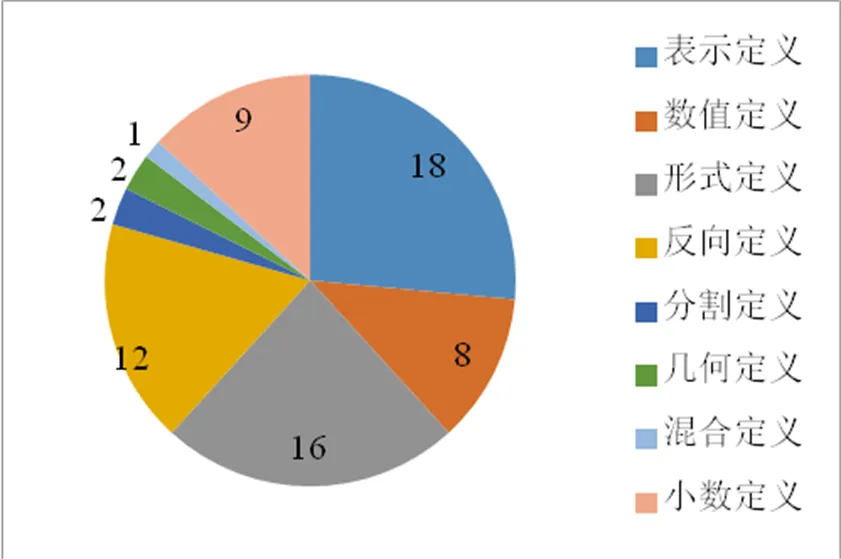
图4 数与式分开定义的八种类型分布
3.1.1 表示定义
表示定义是用“不能用整数或分数表示”来定义无理数,占数式分离定义的26%,不同教科书中略有不同.如Lacroix(1831)给出的定义.Davies(1835)也给出了类似的定义,并第一次给出了非完全平方数的正平方根不能用分数表示的证明,其证法与现行教科书中的证法略有不同,证法如下:
这里用到了数论中的一个定理:“如果一个整数整除两个整数的乘积,且与其中一个互素,则整除另外一个整数.”这些定义都只涉及无理数的一种类型——二次根号型,直到Sherwin(1841)才提到“除了平方根外,其它次数的方根,与单位1没有公因数的也称为无理数”.Gillet(1896)则首次提及“根号型”以外的无理数,将无理数定义为“不能用整数或分数表示的数,也称为不可公度数”,并指出了“不尽根”与“不可公度数”的区别——不尽根是不可公度数,但有许多不可公度数并非不尽根或不尽根的组合,如π、e.
3.1.2 数值定义
这一类定义对无理数的认识基本都局限于“根号型”,认为无理数的值不能精确获得,只能得到其近似值,故以“值不能精确获得”来定义无理数,并将“无理数”等同于“不尽根”,约占12%.如Robinson(1866)将“无理数”定义为“一个非完全平方数的方根,其根值不能精确获得或表示”.这种定义方式在各个时间段均有出现,但较多出现在19世纪早中期.1900年后逐渐消失,仅出现两次,在Hawkers(1918)中提到“一个用根号表示的数,其根值不能精确获得,这种用根号表征的数就是无理数”.
3.1.3 形式定义
部分教科书对无理数的定义停留在对其根式形式的描述,如Thomson(1880)给出的定义是:“非完全平方数的根称为不尽根,也常叫做无理量”;Taylor(1900)给出的定义是:“一个非次幂的数的次方根,称为不可公度方根或无理数”;Wells(1906)给出的定义是:“无理数是一个包含不尽根的数”;类似这样的定义,均把它归为“形式定义”,约占24%.
值得一提的是,Taylor(1900)对无理数和不可公度数进行了错误的区分,书中写道:“一个无理数或其他数,不是整数或分数的称为不可公度数.”即无理数是不可公度数的一部分,显然这是错误的,虽然之前的Gillet(1896)已对“不尽根”和“不可公度”进行了区分.可见,一个数学定义从形成到被广泛接受,会经历一个反复曲折的过程.
3.1.4 反向定义
一些教科书先定义有理数,然后将无理数定义为“除有理数以外的数”,研究者将这一类定义归为“反向定义”,约占18%.研究者将它与“表示定义”区分开来,是由于他们对“有理数”的定义不同,导致对“无理数”的定义也不同,从中可以看出早期人们对数的认识的局限性.例如,Dickson(1902)给出的定义是“有理数是正的和负的整数和分数,其他数都称为无理数.”根据这一定义,“0”应归为无理数,所以该定义的问题在于忽略了“0”的定义.类似的定义还出现在Cajori & Odell(1916)、Hawkers(1918)中.
在今天看来,Marsh(1907)的定义相对完善:“所有的整数和分数称为有理量,所有其它的数称为无理量.”按照这个定义,很容易判断应该将“0”归为有理数一类.但这也仅是用今天的知识做出的判断.有理由相信,在20世纪初期,人们对“0”的认识并不充分,常常忽略“0”的存在.如Lyman(1917)先定义虚数为“负数的偶次方根”,再定义实数“包括所有的正整数和负整数,正分数和负分数,除负数的偶次方根以外的所有方根数”,再定义有理数和无理数“实数分为有理数和无理数,能用整数或者两个整数的商表示的数称为有理数,其它实数称为无理数.”从其“实数”定义中,无法确定“0”属于哪一类,而从其有理数和无理数定义中,用现在的数学观可以判断“0”应归为有理数类.前后的矛盾表明,作者在定义有理数时并没有考虑“0”,更确切地说,早期教科书中存在“0是否是整数”的问题.
3.1.5 分割定义
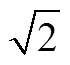
其次,给出有理数的两种不同分割.
最后,给出无理数的定义:

该教科书后续还指出,有理数和无理数统称为实数,第一次建立实数理论体系,并证明了实数是有序的、稠密的、连续的数集.
3.1.6 几何定义
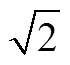

图5 Wilczynski & Slaught(1916)中的几何表示
正无理数被定义为上线段的长度不是有理数的数.又指出,上线段对应的是正数(正有理数或正无理数),反过来每一个正数都对应上的线段.无理数可以看成对应不可公度线段的存在,并介绍了数的发展历史.在另一章“线性函数和级数”中提到如果无理数表示成小数,则它的小数位不能循环也不是有限的.虽然早在17世纪,笛卡尔创立了坐标系,负数得到了几何解释和实际意义,但在约200年后的这本教科书中,依然忽视负无理数的存在和负无理数的几何表示,仅定义了正无理数.
类似的定义方式还出现在Schultze(1925)中,但与上述定义有所不同,给出了负数的几何表示.
3.1.7 混合定义
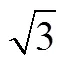
3.1.8 小数定义
“小数定义”是指应用小数表征的定义,代表了人们认识无理数的又一个新阶段,约占13%.Merrill & Smith(1923)最早给出构造的无限不循环小数之例,将无理数定义为“形如0.313 113 111 311 113……,0.487 488 748 887……,这样的数称为无理数”,并指出这样的数不是不合理的,而是不能用比来表征的数.易见,上述定义是不完善的.Miller & Thrall(1950)第一次正式用“无限不循环小数”来定义无理数.表2列举了100种教科书中出现的各种形式的小数定义.

表2 不同形式的小数定义
从中可见,用“无限不循环小数”来定义无理数并非一蹴而就,从1923年第一次出现构造的无限不循环小数到“无限不循环小数”定义的出现,经历了27年;而50年代末开始,“无限不循环小数”定义才被教科书广泛采用,且凡是采用小数定义的教科书中都会另外加以说明无理数不能用分数和整数表示.
3.2 不区分数与式的定义
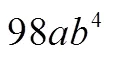
不区分数与式的定义主要分为两类:“数值定义”和“形式定义”.与区分数与式的定义分类原则类似,不再赘述.其中,“数值定义”约占56%,而“形式定义”约占44%,两者基本持平.
4 分布及讨论
4.1 分布
除分割定义仅出现在大学教科书中外,其余定义在中学和大学教科书中均有出现.小数定义最早出现在中学教科书中,后陆续出现在大学教科书中,而在1960年后均出现在中学教科书中.反向定义均出现在1900年后,且若排除“0”的影响,反向定义基本等同于将无理数定义为“不能用整数或分数表示的数”,因此将“反向定义”归为“表示定义”,而“几何定义”、“分割定义”、“混合定义”这3类都出现在1900年后,且各自仅出现一次或两次,故暂且不予考虑.若将“区分数与式的定义”和“不区分数与式的定义”两种情形合在一起,以30年为单位,则其中的“表示定义”、“数值定义”、“形式定义”和“小数定义”的分布情况如图6所示.
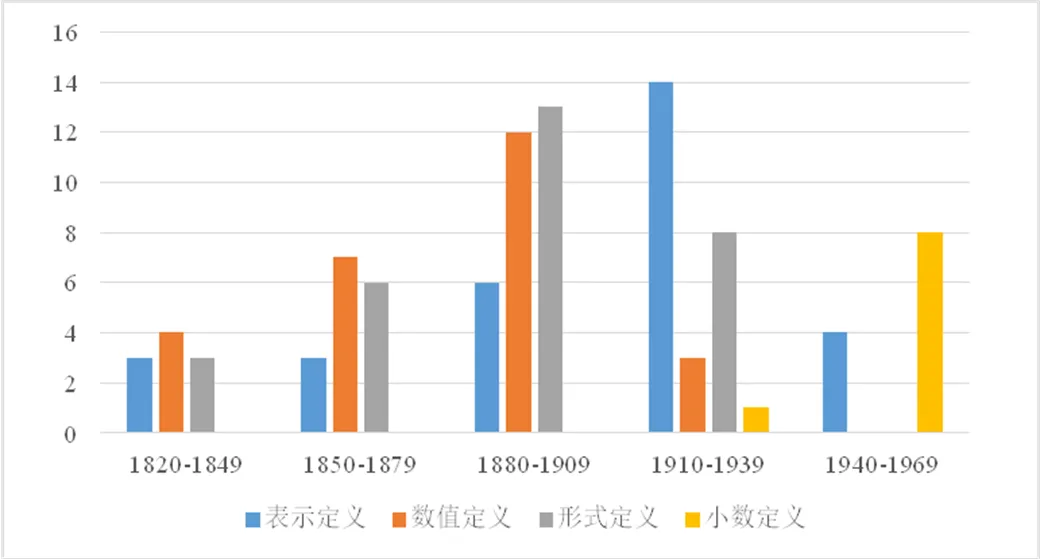
图6 3类定义的时间分布
图7给出教科书所呈现的无理数类型的演进过程.
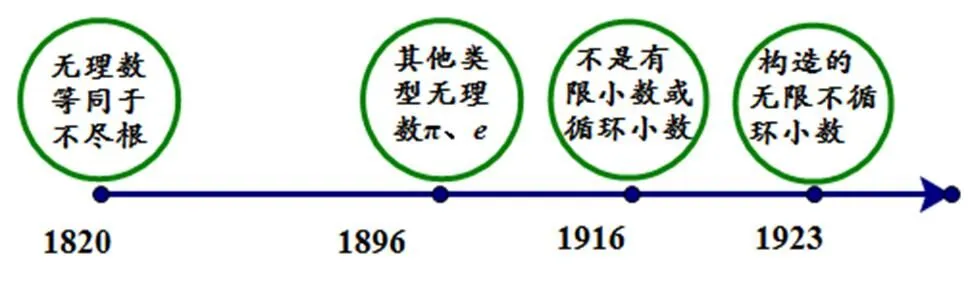
图7 教科书中无理数类型的演变
4.2 无理数理论的历史
公元前470年左右,毕达哥拉斯学派发现无理数的存在,在此后的很长时间内,虽然数学家们对无理数的使用越来越广泛,但对无理数究竟是不是真正的数一直存在分歧,直到18世纪,数学家们仍然没有弄清楚无理数的概念.
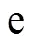
19世纪是无理数理论体系从模糊到逐渐清晰的时期.1821年,柯西(A. L. Cauchy,1789—1897)用有理数序列的极限定义无理数,但根据他的定义,该无理数应是预先给定的数.1872年,康托尔(G. Cantor,1845—1918)引入实数的概念,用有理数的“基本序列”来定义无理数,他证明了每一基本序列都存在极限,该极限若不是有理数,则定义了无理数.戴德金则吸取了柯西的教训,避免采用极限方法,在直线划分的启发下采用分割有理数来定义无理数.魏尔斯特拉斯(F. Weierstrass,1815—1897)同样避免使用极限概念,用递增有界数列定义无理数.斯托尔兹(O. Stolz,1842—1905)证明了“每一个无理数均可表示成不循环小数”,并认为可用这一事实来定义无理数.
4.3 讨论
综上,数值定义和形式定义对无理数的认识均停留在表层,体现了早期人们对无理数认识的局限性,而表示定义是无理数发现和定义的起源,小数定义是实数理论体系完备后新出现的定义,从表示定义到小数定义也体现了数学发展从潜无穷到实无穷的转变.在漫长的一个半世纪里,无理数始于数值定义而终于小数定义,反映了人们对无理数的认识,经历了从模糊到逐渐清晰的过程.“形式定义”由于其表征直观而出现于每一个时期,“数值定义”曾一度占据上风,但随着无理数理论体系的建立而逐渐销声匿迹.19世纪早期,虽然无理数的“表示定义”相对比重最高,但人们对无理数的认识依然停留在“不尽根”,基本上将无理数与不尽根混为一谈.在后续的一百年间,该定义所占比重有下降趋势.直到19世纪末,实数理论体系建立,重新占据主要地位,并与小数定义并驾齐驱.教科书对无理数的定义及表征的发展,虽有一定的滞后性,但与无理数理论的发展基本一致.无理数表征的演进历史表明,今日学生对无理数的认识具有较为显著的历史相似性.
5 结论与启示
无理数并非“没有道理”,只是“不能用整数或分数表示”,历史上人们对无理数的认识,最早是从“根号型”开始,后续陆续发现其他类型的无理数的存在,如:π、e等.而学生对无理数的认识与无理数的发展具有历史相似性,已有研究表明,虽然高中阶段和大学阶段会学习很多除“根号型”和π以外的无理数,但学生最为熟悉的还是最初的这两种类型.现代教科书中均采用“无限不循环小数”来定义无理数,这已完全脱离了无理数最初的起源,是“深加工”的结果,学生对无理数的理解往往停留在表面,仅会从形式上判断是不是无理数,而不能从知识的本质上理解无理数的定义.而早期教科书无理数定义从不完善到完善的过程,为今日的教科书编写和课堂教学均带来启示.
5.1 对教科书编写的启示
首先,教科书是我们向前延续传输知识的有力工具,教科书中无理数定义的演变过程基本反映了数学研究领域无理数定义的演进过程.但一些教科书中也出现了错误和倒退现象,如前述所提对“0”的忽略和几何定义中对负无理数的忽略.所以这就要求教科书编写者对当下的数学学科领域的发展有一定的了解,才能把握教材知识内容的正确性和适切性.
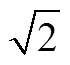
5.2 对教学设计的启示
可以借鉴无理数定义的发展过程,运用重构历史的方式来设计无理数概念的教学,让学生从现实问题中体会无理数存在的必要性和无理数与有理数的区别,在此基础上给无理数下定义——不能用分数或整数表示,再根据有理数的小数表征,揭示无理数的小数表征,加深学生对无理数概念和表征的理解.同时可以附加式运用历史知识,介绍无理数发展的历史,让学生了解数学并非无中生有,而是从现实生活中产生.历史上无理数概念的曲折发展,也可以渗透数学学科的德育功能,让学生体会人们对任何新事物的认识都是伴随着曲折往复而螺旋上升,同样学习也是螺旋上升的过程.虽高中及后续不再专门学习无理数,但在认识新类型的无理数时,需要教师帮助学生进一步理解无理数的类型.同时,鉴于初中知识的深度,不可能详细讲述无理数其他更多的定义,教师可以设下伏笔,以备学生在后续学习中完善对无理数以及实数的认识.
[1] ZAZKIS R, SIROTIC N. Making sense of irrational numbers: focusing on representation [M] // HOINES M J, FUGLESTAD A B. Proceedings of the 28th international conference for psychology of mathematics education. Norway: Bergen, 2004: 497-504.
[2] ZAZKIS R. Representing members: prime and irrational [J]. International Journal of Mathematical Education in Science and Technology, 2005, 36(2-3): 207-218.
[3] SIROTIC N, ZAZKIS R. Irrational numbers: the gap between formal and intuitive knowledge [J]. Educational Studies in Mathematics, 2004, 65(1): 49-76.
[4] CAJORI F. The pedagogic value of the history of physics [J]. The School Review, 1899, 7(5): 278-285.
[5] SMITH D E. Teaching of elementary mathematics [M]. New York: The Macmillan Company, 1900: 42-43.
[6] 庞雅丽,李士锜.初三学生关于无理数的信念的调查研究[J].数学教育学报,2009,18(4):38-41.
[7] 冯璟,陈月兰.无理数的认识——对64名职前数学教师的调查研究[J].中学数学月刊,2010(2):6-8.
[8] 陈月兰,杨秀娟.初中生对无理数概念的理解[J].上海中学教学,2008(6):11-13.
[9] 克莱因 M.古今数学思想:第三册[M].邓东皋,张恭庆,译.上海:上海科学技术出版社,2014:149-153.
[10] LACROIX S F. Elements of algebra [M]. Boston: Hilliard, Gray, Little and Wilkins, 1831: 116.
[11] BOURDON M. Elements of algebra [M]. Boston: Hilliard, Gray, Little, and Wilkins, 1831: 106.
[12] DAVIES C. Elements of algebra [M]. New York: Wiley & Long, 1835: 127.
[13] SHERWIN T. An elementary treatise on algebra[M]. Boston: Hall and Whiting, 1841: 140.
[14] HACKLER C W. An elementary treatise on algebra [M]. New York: Harper & Brothers, 1847: 52.
[15] ROBINSON H N. New elementary algebra [M]. New York: Ivison Phinney, Blakeman, & Co., 1866: 24.
[16] THOMSON J B. New practical algebra [M]. New York: Clark & Maynard, 1880: 149.
[17] WENTWORTH G A. A college algebra [M]. Boston: Ginn & Company, 1892: 89.
[18] GILLET J A.Elementary algebra [M]. New York: H. Holt & Company, 1896: 176.
[19] TAYLOR J M. Elements of algebra [M]. Boston: Allyn and Bacon, 1900: 250.
[20] MILNE W J. Advanced algebra for college and schools [M]. New York: American Book Company, 1902: 19.
[21] DICKSON L E. College algebra [M]. New York: J. Wiley & Sons, 1902: 2.
[22] FINE H B. A college algebra [M]. Boston: Ginn & Company, 1904: 41.
[23] WELLS W. Algebra for secondary schools [M]. Boston: D. C. Health & Company, 1906: 222.
[24] TANNER J H. High school algebra [M]. New York: American Book Company, 1907: 235.
[25] MARSH W R. Elementary algebra [M]. New York: C. Scribner’s Sons, 1907: 228.
[26] YOUNG J W A, JACKSON L L. Elementary algebra [M]. New York: D. Appleton & Company, 1910: 42.
[27] LONG E, BRENKE W C. Algebra, first course [M]. New York: The Century Co., 1913: 176.
[28] CAJORI F, ODELL L R. Elementary algebra [M]. New York: Macmillan, 1916: 91.
[29] WILCZYNSKI E J, SLAUGHT H E. College algebra [M]. Boston: Allyn & Bacon, 1916: 19.
[30] LYMAN D. Elementary algebra [M]. New York: American Book Company, 1917: 33.
[31] HAWKERS H E. Second course in algebra [M]. Boston: Ginn & Company, 1918: 109.
[32] MERRILL H A, SMITH C E. A first course in higher algebra [M]. New York: The Macmillan Company, 1923: 132.
[33] SCHULTZE A. Elementary and intermediate algebra [M]. New York: The Macmillan Company, 1925: 355.
[34] WEISS M J. Higher algebra for the undergraduate [M]. New York: J. Wiley, 1949: 29.
[35] MILLER E B, THRALL R M. College algebra [M]. New York: Ronald Press Company, 1950: 15.
[36] FEINSTEIN I K, MURPHY K H. College algebra [M]. Ames: Iowa, Littlefield, Adams, 1957: 3.
[37] BRUMFIEL C F, EICHOLZ R E, SHANKS M E. Algebra I [M]. Mass.: Addison-Wesley Publishing Company, 1961: 277.
[38] FINE H B. College algebra [M]. New York: Dover Publications, 1961: 43.
[39] MILLER I, GREEN S. Algebra and trigonometry [M]. Englewood Cliffs, N. J.: Prentice-Hall, 1962: 19.
[40] KOO D, BLYTH M I, BURCHENAL J M. First course in modern algebra [M]. New York: F. Ungar Publishing Company, 1963: 173.
[责任编校:周学智]
Concept of Irrational Numbers in Early Western Textbooks
LI Xiao-ni, WANG Xiao-qin
(College of Teacher Education, East China Normal University, Shanghai 200062, China)
During the period 1820--1969, one hundred algebra textbooks in America’s middle schools and colleges had given eight definitions of irrational numbers. The definition that irrational numbers were infinite non-repeating decimals began at 1920s. The previous evolution of the concept of irrational numbers provided reference for the present textbook compiling and teaching. The newly-compiled textbook should reflect the diversity of definitions of irrational numbers and reveal that irrational numbers couldn’t be expressed by integers and fractions. Furthermore, drawing on the development of irrational number, we could reconstruct the history in class to design the concept teaching of irrational numbers to promote students’ overall understanding and grasping of irrational numbers as well as the real numbers.
irrational numbers; irrational expressions; surds; definitions
G40–059.3
A
1004–9894(2017)06–0086–06
栗小妮,汪晓勤.美国早期教科书中的无理数概念[J].数学教育学报,2017,26(6):86-91.
2017–06–26
上海市教育科学研究重大项目——中小学数学教科书的有效设计子课题——中小学数学教科书中数学文化素材的案例设计(D1508)
栗小妮(1984—),女,山西晋城人,博士生,主要从事数学史与数学教育研究.
