《2017年普通高中数学学科教学与评价指导意见》解析

吕世虎，王尚志，胡凤娟，缴志清，沈 婕，申 铁，康 杰，丁明怡，韩际清，邵丽云，孙孝武，贺航飞



《2017年普通高中数学学科教学与评价指导意见》解析

吕世虎1，王尚志2，胡凤娟2，缴志清3，沈 婕4，申 铁4，康 杰5，丁明怡5，韩际清6，邵丽云7，孙孝武8，贺航飞9

（1．西北师范大学，甘肃兰州 730070；2．首都师范大学，北京 100048；3．河北省教育科学研究所，河北石家庄 050000；4．天津市教委教研室，天津 300387；5．北京教育科学研究院基础教育教学研究中心，北京 100045；6．山东省教育科学研究院，山东济南 250002；7．山东省实验中学，山东济南 250001；8．海南省教育研究培训院，海南海口 571100；9．海南省海口中学，海南海口 571158）

《2017年普通高中数学学科教学与评价指导意见》是在高考招生制度综合改革实验深入推进和普通高中课程方案与课程标准修订取得阶段性成果的背景下，适应新理念、新要求、新高考，旧教材的现状，供高考招生制度综合改革试点省市，在新修订的普通高中课程方案以及普通高中数学课程标准实施前的过渡时期使用的指导性文件．该文件包括理念与目标、课程结构、课程内容、实施建议、附录5个部分．理念与目标、课程结构、实施建议、附录部分的相关内容，与高中数学课程标准修订稿的阶段性成果一致．课程内容以现行高中数学课程标准实验稿的内容为基础作了适当的删减和调整．必修课程内容对现行内容作了删减，保留部分与现行内容要求一致．选修Ⅰ课程内容，在现行文科数学课程内容基础上作了删减和扩充，扩充部分包括现行必修课程的部分内容和理科数学部分内容，其中理科数学一些内容降低了要求．选修Ⅱ课程采用高中数学课程标准修订稿的内容．

高中数学；教学；评价；指导意见

2017年秋，北京、天津、山东、海南进入高考招生制度综合改革试点，为积极稳妥地推动落实本次高考招生制度综合改革实验，依据教育部《普通高中课程方案（修订稿）》《普通高中数学课程标准（修订稿）》（以下简称《标准修订稿》）等文件的精神，以及教育部教材局《2017年启动高考综合改革试点省新高一各学科课程教学内容指导意见研制工作方案》（以下简称《工作方案》）的要求，数学学科研制组（以下简称“研制组”）研制了《2017年普通高中数学学科教学与评价指导意见》（以下简称《指导意见》），供高考招生制度综合改革试点省市，在新修订的普通高中课程方案以及普通高中数学课程标准实施前的过渡时期使用．《指导意见》作为试点省份今后几年高中数学教学与评价的指导性文件，与现行《普通高中数学课程标准（实验）》（以下简称《标准实验稿》）相比，在理念与目标、课程结构、课程内容和实施建议等方面有较大变化，准确把握这些变化，对于试点省份有效落实《指导意见》具有重要作用．这里拟从研制背景与历程、理念与目标、课程结构、课程内容、实施建议等方面对《指导意见》进行解析．

1 《指导意见》研制的背景与历程

2014年9月，国务院发布了《国务院关于深化考试招生制度改革的实施意见》（以下简称《实施意见》），新一轮考试招生制度改革全面启动．上海、浙江于2014年先行高考综合改革试点，2017年6月已按照新的高考方案进行考试招生．2017年，北京、天津、山东、海南4个省市进入高考招生制度综合改革试点，在秋季入学的高一新生中启动新高考方案，2020年将按照新的高考方案进行考试招生．《实施意见》在高考科目设置、招生录取机制等方面有一系列改革措施[1]．特别是高考不分文理科，对数学学科的影响最大．

2014年3月，教育部发布《教育部关于全面深化课程改革落实立德树人根本任务的意见》，全方位启动课程改革．普通高中课程方案与课程标准修订作为深化课程改革的突破口先行启动实施．目前，普通高中课程方案和各科课程标准修订工作基本完成．高中课程方案和各科课程标准修订贯彻了《实施意见》的精神，与新一轮考试招生制度改革完全对接．

为顺利推进北京、天津、山东、海南4个试点省市高考招生制度综合改革，实现向新修订的高中课程方案和数学课程标准的平稳过渡，教育部教材局于2017年4月，组织高中课程方案修订专家、课程标准修订专家、试点省的学科教研员、教育管理专家，研究调整现行高中课程方案和各学科教学内容，制定各学科教学与评价指导意见．

《指导意见》研制的过程分以下几个阶段：

第一阶段：学习领会《实施意见》和《工作方案》的精神，统一认识，明确工作任务．

第二阶段：确定《指导意见》研制的指导思想和制定原则．

第三阶段：由天津市教研室提出《指导意见》初步方案，经研制组讨论修改，形成《指导意见》初稿．

第四阶段：召开研讨会，征求四省市教研部门、一线教师、课程修订组专家对《指导意见》初稿的意见，并据此进行修改，形成《指导意见》修改稿．

第五阶段：征求教育部有关司局（包括考试中心）对《指导意见》修改稿的意见，经修改完善后形成《指导意见》定稿，提交教育部教材局．

2 《指导意见》研制的指导思想与原则

研制组根据国务院《实施意见》和教育部教材局《工作方案》的要求，结合高中数学课程标准修订的新理念、新要求以及新高考和旧教材，确定了研制《指导意见》的指导思想：（1）以《标准修订稿》的理念、目标、核心素养、课程结构、实施建议为主线，撰写《指导意见》；（2）实现与《标准实验稿》、教材、教学、评价的平稳过渡；（3）实现与《标准修订稿）》实施、高考改革的平稳过渡．

根据指导思想，确定了课程内容调整的原则：（1）《指导意见》的课程内容与《标准修订稿》的课程内容尽量保持一致；（2）《指导意见》只对必修与选修Ⅰ课程的内容作界定，不对模块和内容顺序作要求，力求使《指导意见》管用、好用；（3）《指导意见》的课程内容尽量保持与现行教材章节一致；（4）《指导意见》选修Ⅰ课程的内容一般按原文科要求，与原文科相比增加的内容适度降低难度；（5）《指导意见》的选修Ⅰ课程中增加对数学建模的要求；（6）《指导意见》选修Ⅱ课程的内容采用《标准修订稿》选修Ⅱ课程的内容．

3 《指导意见》中的理念与目标

《指导意见》文本包括理念与目标、课程结构、课程内容、实施建议、附录5个部分．在理念与目标部分，阐述了课程理念、课程目标、数学核心素养，这些内容与高中数学课程标准修订过程中的阶段性成果一致．

课程理念即课程指导思想，包括4条：（1）学生发展为本，立德树人，提升素养．这是理念的总纲，是总体指导思想；（2）优化课程结构，突出主线，精选内容．这是确定课程结构、选择课程内容的指导思想；（3）把握数学本质，启发思考，改进教学．这是教与学的指导思想；（4）重视过程评价，突出素养，提高质量．这是评价的指导思想．

课程目标可以概括为3个层次：四基、四能；六个核心素养，三会；数学精神（情感态度价值观）．四基、四能是数学核心素养形成与生长的沃土，三会是核心素养的具体体现，数学精神是核心素养的升华．3个层次构成以数学核心素养为中心的完整数学课程目标体系[2]．

数学素养部分阐述了数学核心素养与数学课程目标的关系以及数学核心素养的内涵、特征和构成要素．数学核心素养是数学课程目标的集中体现．数学核心素养是适应个人终身发展和社会发展需要的具有数学基本特征的思维品质与关键能力以及情感、态度与价值观的综合体现，是在数学学习和应用的过程中逐步形成和发展的．数学核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析．这些数学核心素养既相对独立、又相互交融，是一个有机的整体．该部分还对6个数学核心素养的内涵、学科价值、具体表现、教育价值等作了阐述．

4 《指导意见》中的课程结构

《指导意见》中，高中数学课程分为必修课程、选修Ⅰ课程和选修Ⅱ课程．课程内容突出函数、几何与代数、统计与概率、数学建模活动与数学探究活动4条主线，它们贯穿必修、选修Ⅰ和选修Ⅱ课程中．数学文化融入课程内容．课程结构如表1所示．

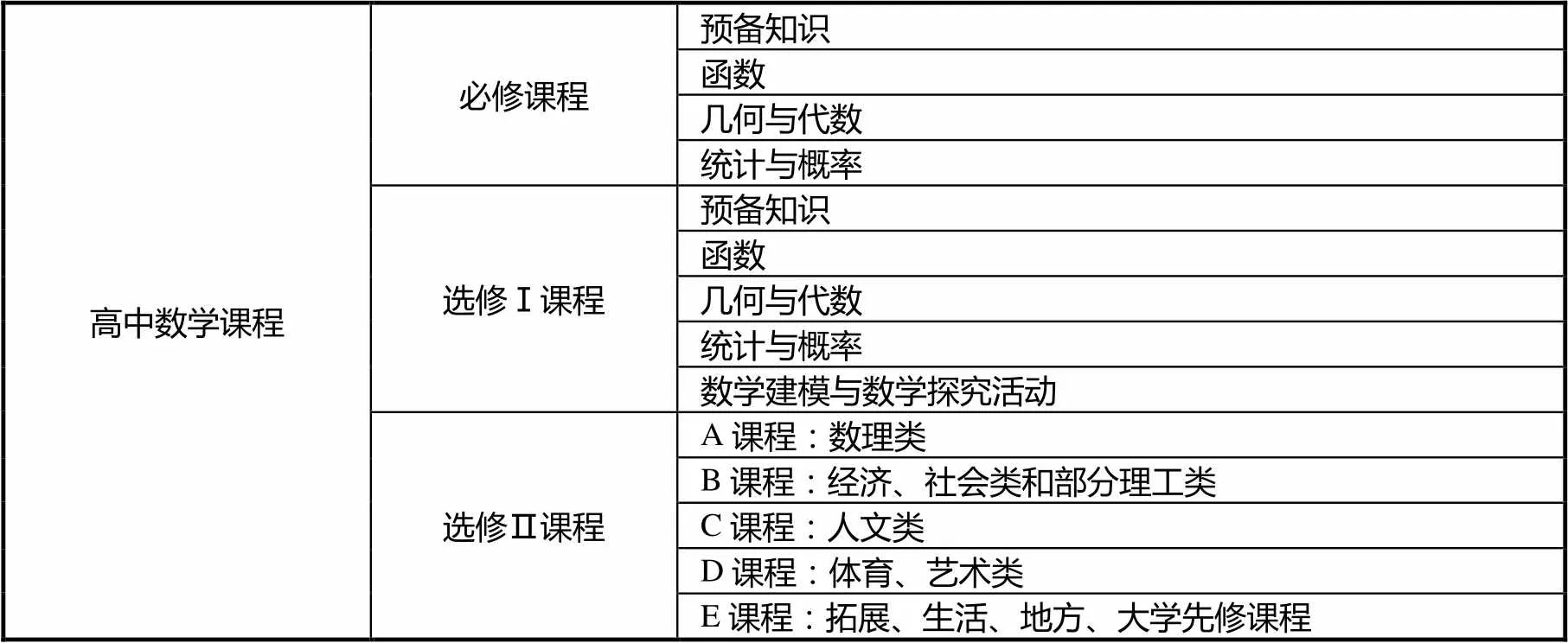
表1 《指导意见》中高中数学课程内容结构

其中，必修课程8学分，选修Ⅰ课程6学分，选修Ⅱ课程6学分．必修课程为学生发展提供共同基础，是高中毕业的数学学业水平考试的内容要求；选修Ⅰ课程是供学生选择的课程，必修课程和选修Ⅰ课程是高考的内容要求；选修Ⅱ课程是由学校根据学校自身情况选择设置的课程，供学生依据个人志趣自主进行选择，分为A、B、C、D、E五类．这些课程为学生确定发展方向提供引导，为学生展示数学才能提供平台，为学生发展数学兴趣提供选择，为大学自主招生提供参考．

上述课程结构，与现行《课标实验稿》不同．《课标实验稿》中采用模块课程结构，高中数学课程分为必修和选修两类，必修课程由5个模块组成，选修课程有4个系列，系列1为文科倾向课程，由两个模块构成，系列2为理科倾向的课程，由3个模块构成，系列3、4由若干专题构成．课程内容组织按照各模块的学分综合配置函数、几何、统计概率、数学建模与数学探究等内容[3]．《指导意见》中是按照函数、几何与代数、统计与概率、数学建模活动与数学探究活动四条主线组织课程内容，不采用模块课程结构．

5 《指导意见》中的课程内容

《指导意见》中的课程内容部分，包括必修课程，选修Ⅰ课程，选修Ⅱ课程3部分．

5.1 必修课程内容

《指导意见》的必修课程分预备知识、函数、几何与代数、统计与概率4部分，8学分，与现行《课标实验稿》相比减少了两个学分，内容也作了删减和调整．具体内容及课时如表2所示．

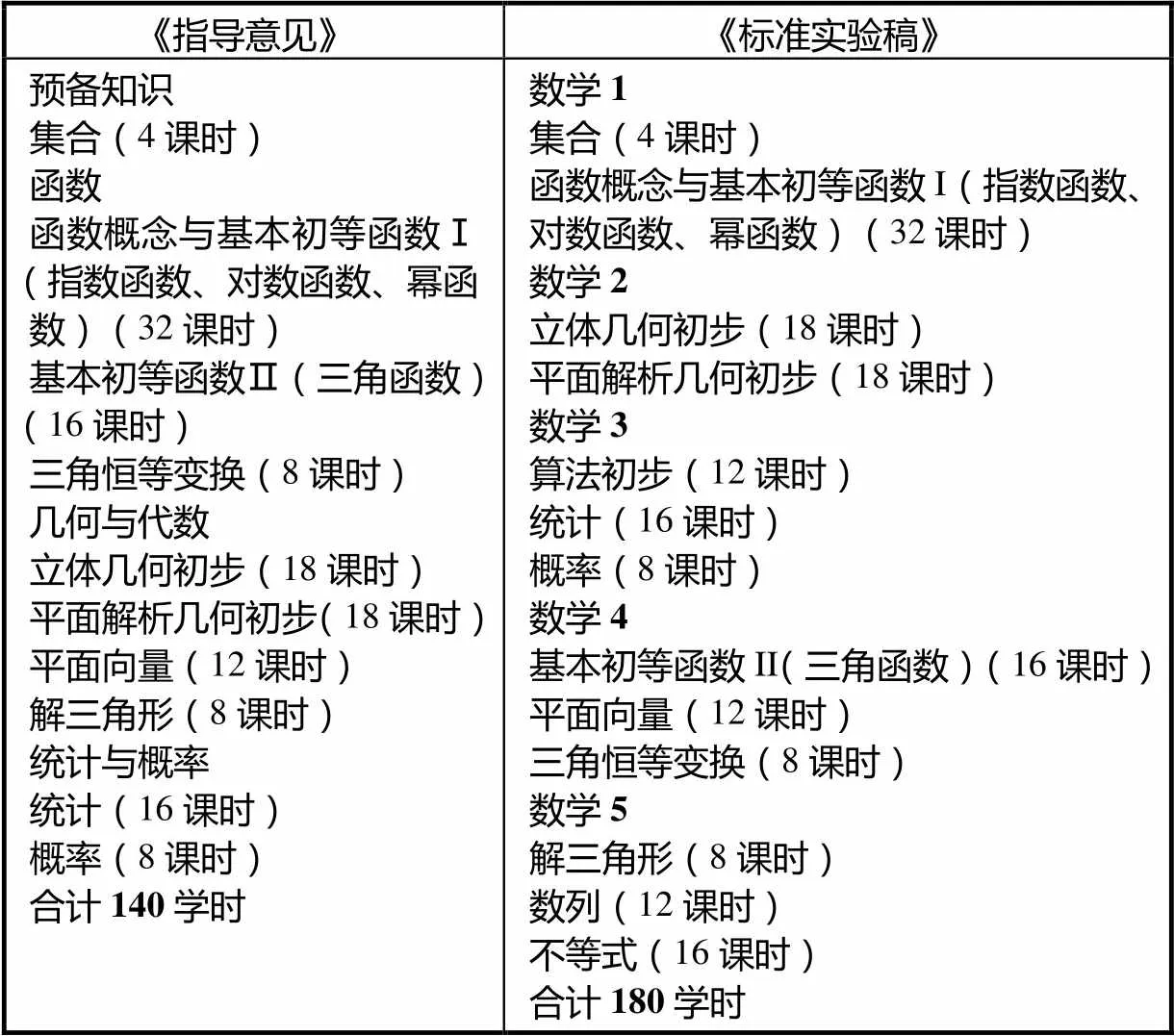
表2 《指导意见》与《课标实验稿》必修课程内容与课时对照

由表2可以看出，《指导意见》必修课程内容在现行《课标实验稿》必修课程内容基础上作了删减，删除了算法初步、数列、不等式等内容，保留部分与《课标实验稿》内容标准要求一致．必修课程总课时约为140学时．

5.2 选修Ⅰ课程内容

《指导意见》的选修Ⅰ课程分预备知识、函数、几何与代数、统计与概率、数学建模与数学探究活动5部分，6学分，与现行《课标实验稿》相比，对文科数学（系列1）内容作了删减，增加了必修课程和理科数学（系列2）中的一些内容．具体内容及课时如表3所示．

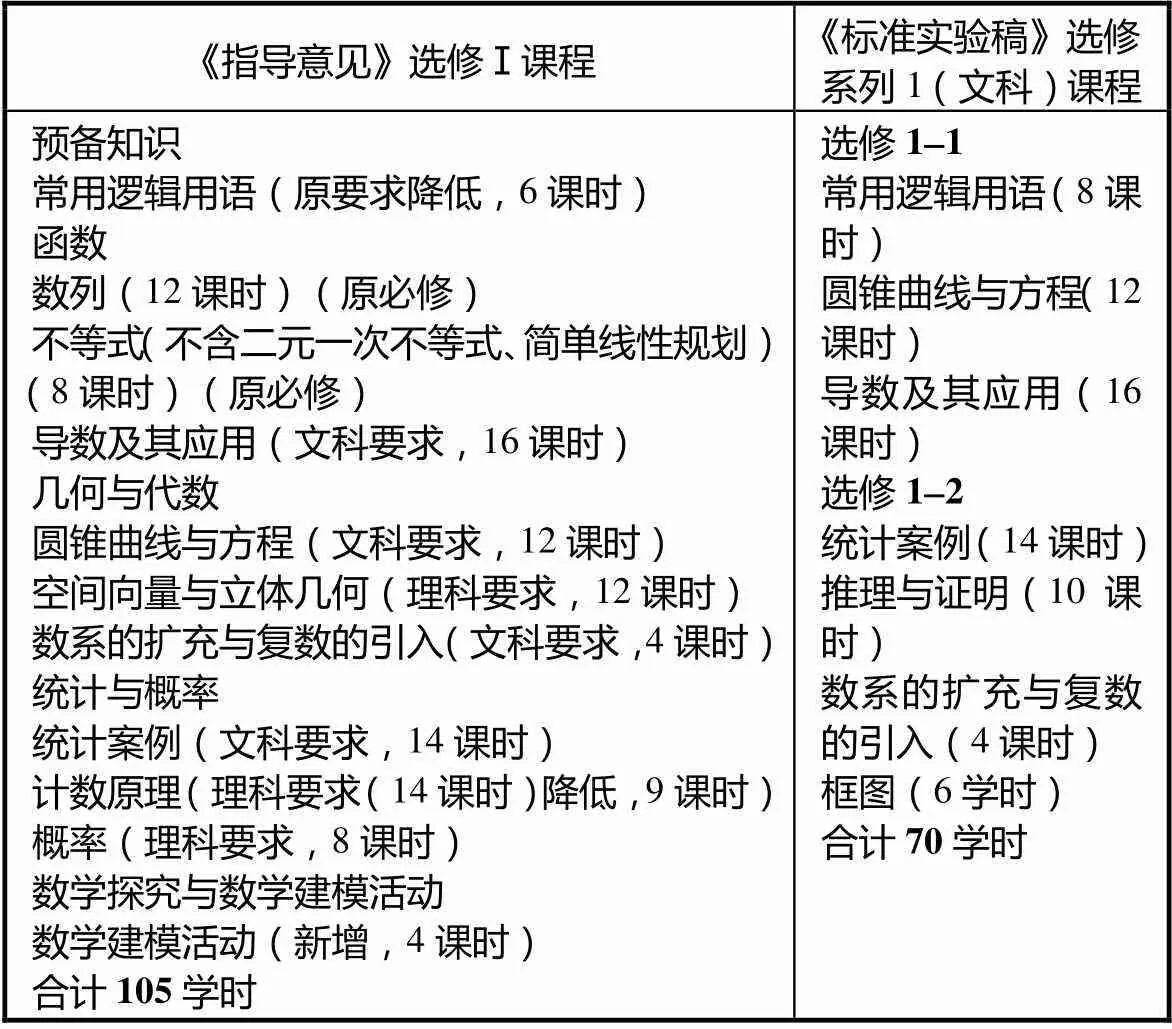
表3 《指导意见》与《课标实验稿》选修Ⅰ课程内容与课时对照

由表3可以看出，《指导意见》选修Ⅰ课程内容，在现行《课标实验稿》文科数学课程内容基础上作了删减和扩充，删除了推理与证明、框图等内容，增加了原必修课程中的数列、不等式（不含二元一次不等式、简单线性规划）的内容以及理科数学中的空间向量与立体几何、计数原理、概率的内容，还新增了数学建模活动的内容．其中，常用逻辑用语比原来文科数学减少了4种命题及其之间的相互关系、简单的逻辑联结词等内容，计数原理比原理科数学减少用计数原理、排列与组合解决简单实际问题的内容，其它内容与《课标实验稿》中相应内容标准要求一致．选修Ⅰ课程总学时约为105学时．

5.3 选修Ⅱ课程内容

《指导意见》选修Ⅱ课程分为A、B、C、D、E五类．A课程包括微积分、空间几何与代数、统计与概率3门课程，其中微积分2.5学分，空间几何与代数2学分，统计与概率1.5学分；B课程包括微积分、空间向量与代数、应用统计、模型4门课程，其中微积分2学分，空间向量与代数1学分，应用统计2学分，模型1学分；C课程包括逻辑推理初步、数学模型、社会调查与数据分析3门课程，每门课程2学分；D课程包括美与数学、音乐中的数学、美术中的数学、体育运动中的数学4门课程，每门课程1学分；E课程包括拓展视野的数学课程（例如，机器人与数学、对称与群、球面上的几何、欧拉公式与闭曲面分类、数列与差分、初等数论初步）、日常生活的数学课程（例如，生活中的数学、家庭理财与数学）、地方特色的数学课程（例如，地方建筑与数学、家乡经济发展的社会调查与数据分析），及大学数学的先修课程（例如，微积分、解析几何与线性代数、概率论与数理统计）等．

《指导意见》选修Ⅱ课程与《课标实验稿》中选修系列3、4相比有较大变化．除了原选修系列3、4中的对称与群、球面上的几何、欧拉公式与闭曲面分类、数列与差分、初等数论初步等专题外，其它内容均为新设置的内容．高中数学标准修订组正在编写选修Ⅱ课程的教材，拟于2018年进行试验．

6 《指导意见》中的实施建议

《指导意见》实施建议包括教学建议、评价建议、考试建议、学校实施建议．

6.1 教学建议

教学建议包括5部分内容：教学目标制定，教学情境创设，教学内容把握，教学方式选择，信息技术运用．这5部分基本上涵盖了教学设计与实施的主要环节．

教学目标制定建议，特别强调了把握核心素养与“四基”目标的关系：数学核心素养是“四基”的继承和发展，“四基”是培养学生数学核心素养的沃土，是发展学生数学核心素养的有效载体，应引导学生理解基础知识，掌握基本技能，感悟数学基本思想，积累数学基本活动经验，促进学生数学核心素养的不断提升；教学情境创设建议，主要强调了情境创设要突出数学本质、提出合适问题、引导学生思考和解决问题；教学内容把握建议，主要强调了整体把握课程内容，抓住主线，特别是开展数学探究、数学建模活动是发展学生数学核心素养的重要路径；教学方式选择建议，主要从3个方面阐述了如何促进学生学会学习才能自觉地发展数学核心素养．第一，教学活动的重心从教转到学．第二，倡导讲授与练习，阅读自学、独立思考、动手实践、自主探索、合作交流等多种学习方式．第三，加强学法指导；信息技术运用建议，主要强调合理使用信息技术解决传统手段不能解决的问题．

6.2 评价建议

评价建议是指日常教学评价建议，包括：评价目的、评价原则、评价方式、评价结果的呈现与利用．

评价建议中，强调了教学评价的目的是通过考察学生学习的成效、进而考察教师教学的成效；通过考察，诊断学生学习过程中的优势与问题、进而诊断教师教学过程中的优势与问题；通过诊断，改进学生的学习行为、进而改进教师教学行为．阐述了日常教学评价应遵循的4个原则：重视学生数学核心素养的达成；重视评价的整体性与阶段性；重视过程评价；关注学生的学习态度．强调教师、学生、家长等多元主体参与评价，使用书面测验、课堂观察、口头测验、开放式活动中的表现、课内外作业等多种方式开展评价，评价结果的呈现与利用要有利于增强学生学习数学的自信心，提高学生学习数学的兴趣，使学生养成良好的学习习惯，促进学生的全面发展．要尽量避免终结性评价的“标签效应”，简单地依据评价结果对学生进行区分；要系统、全面、客观地反映学生在数学核心素养发展上的成长过程和水平特征，为每个学生提供长期、具体、可行的指导和改进建议．

6.3 考试建议

考试建议部分，对高中毕业的数学学业水平考试、数学高考的命题从命题原则和命题路径两方面提出建议．

命题原则主要强调：注重对学生数学核心素养的考查，注重数学本质、通性通法，淡化解题技巧，融入数学文化；应有一定数量的应用问题，考查学生的思维过程、实践能力和创新意识；科学设计选择题、填空题的题量．

命题路径主要强调：构建基于数学核心素养测试的评价框架；编制基于数学核心素养的试题．

6.4 学校实施建议

学校实施建议主要强调：（1）加强学校课程建设．学校应根据自身的情况，推动国家课程校本化，建设有特色的校本课程，适应学生多样化发展的需求，促进学生全面发展；（2）形成有效的课程管理机制．学校要形成有效的机制，处理好备课组和教研组的关系，使得备课组与教研组协同、高效工作，为数学课程的实施提供保障．学校要为课程的选择提供必要的教学条件，形成相应的管理制度，充分利用社会资源以满足学生的学习需求；（3）加强数学教师的专业发展和团队建设．学校要加强对数学教师的培训，制定教师培训计划，包括校内培训、外出研学、与高校联合培养等，从经费和时间上给予充分的保障，提升教师的专业水平．学校要加强培养数学骨干教师，充分发挥骨干教师的作用，关注青年教师的成长，注重发展教师的数学教育理论、实践能力等，形成高效、专业的教师团队；（4）开展有针对性的数学教研活动．教研组应定期开展教研活动，针对日常教学中的问题，采取灵活多样的教研方式加以解决，通过课题研究、教学论文评比、教学案例评比、优质课比赛等活动提高课程的开设质量．

《指导意见》的附录C中，给出了几个版本教材使用说明．必修课程采用现行必修数学教材，对于现行必修教材的内容，除删除的内容外，基本上整章节保留．为选用教材方便，选修Ⅰ课程使用现行理科数学教材，根据《指导意见》要求，删除相关内容或降低要求．

高考招生制度综合改革，实施文理不分科考试，特别是2017年进入试点的省市，要在新理念、新要求、新高考背景下，使用旧教材．新理念、新要求的突出体现是，高中数学教学要落实发展学生数学核心素养的育人目标．显然，高中数学教学中，以关注知识点为主的课堂教学设计、以传授知识和训练解题为主的讲授式教学方式等难以适应新要求．《指导意见》提倡，高中数学教师要整体把握课程内容，根据内容主线按主题/单元设计教学活动[4]，以问题解决为主，将数学建模与数学探究活动作为落实发展学生数学核心素养目标的重要路径．这对教师的教学设计、教学方式、教学活动组织形式等都提出了挑战，同时也给教师专业发展提供了机遇．希望广大老师积极应对挑战，抓住机遇，开展探索研究，不断提升自身的专业水平．数学学科研制组将为广大教师提供支持和帮助，与大家一起探索与实践，落实好《指导意见》．

[1] 中华人民共和国国务院．国务院关于深化考试招生制度改革的实施意见（国发[2014]35号）[EB/OL]．（2014-09-04）[2017-11-01]．http://www.51meishu.com/html/20140904/84234.html.

[2] 吕世虎，吴振英．数学核心素养的内涵及其体系构建[J]．课程·教材·教法，2017，37（9）：12-17．

[3] 中华人民共和国教育部．普通高中数学课程标准（实验）[M]．北京：人民教育出版社，2003：5-9．

[4] 吕世虎，杨婷，吴振英．数学单元教学设计的内涵、特征以及基本操作步骤[J]．当代教育与文化，2016，8（4）：41-46．

[责任编校：周学智]

Analysis of

LV Shi-hu1, WANG Shang-zhi2, HU Feng-juan2, JIAO Zhi-qing3,SHEN Jie4, SHEN Tie4, KANG Jie5, DING Ming-yi5, HAN Ji-qing6, SHAO Li-yun7, SUN Xiao-wu8, HE Hang-fei9

(1. Northwest Normal University, Gansu Lanzhou 730070, China; 2. Capital Normal University, Beijing 100048, China; 3. Education Research Institute of Hebei Province, Hebei Shijiazhuang 050000, China; 4. Education Department of Tianjin Education Committee, Tianjin 300387, China; 5. Basic Education Research Center of Beijing Education Institute, Beijing 100045, China; 6. Education Research Institute of Shandong Province, Shandong Ji’nan 250002, China; 7. Experimental High School of Shandong Province, Shandong Ji’nan 250001, China; 8. Education Research and Training Institute of Hainan Province, Hainan Haikou 571100, China; 9. Haikou High School of Hainan Province, Hainan Haikou 571158, China)

was an instructive document, which was under the background of the in-depth propelling of the comprehensive reform experiment carried out in the college entrance examination enrollment system and some periodical results achieved in the senior high school curriculum scheme and the revision of the curriculum standards. The document was adapted to the new concept, new requirements, new college entrance examination and the current situation of the old teaching materials. It could be used by the provinces and cites which had been the comprehensive pilot reforms on college entrance examination enrollment system in the transitional period before the newly-revised senior high school curriculum scheme and the senior high school mathematical curriculum standards were implemented. The document included five parts, which were concepts and objectives, curriculum structure, curriculum contents, implementing proposals and appendixes, completely identical with the revised edition of senior high school mathematical curriculum standards. The contents of the course had been appropriately deleted and expanded on the basis of the current trial draft of the senior high school mathematical curriculum standard. The contents of the compulsory course had been deleted, and the reservation part was consistent with the current content requirements. The contents of elective courseⅠwere deleted and expanded on the basis of the current liberal arts mathematical curriculum. The expansion sections included part of the current compulsory courses and the science mathematics, while the science mathematicslowers its requirements. Elective course II employs some part of the revised edition of senior high school mathematical curriculum standard.

senior high school mathematics; teaching; evaluation; guidance

G632.0

A

1004–9894（2017）06–0001–05

吕世虎，王尚志，胡凤娟，等．《2017年普通高中数学学科教学与评价指导意见》解析[J]．数学教育学报，2017，26（6）：1-5．

2017–11–06

吕世虎（1963—），男，甘肃平凉人，教授，教育学博士，博士生导师，主要从事数学课程与教学论、数学教育史研究．

本文经数学学科研制组集体讨论，由吕世虎（西北师范大学）执笔完成．研制组组长：王尚志（首都师范大学），学术秘书：胡凤娟（首都师范大学）．成员：吕世虎（西北师范大学），缴志清（河北省教育科学研究所），沈婕、申铁（天津市教委教研室），康杰、丁明怡（北京教科院基教研中心），韩际清（山东省教育科学研究院），邵丽云（山东省实验中学），孙孝武（海南省教育研究培训院），贺航飞（海南海口中学）