高中三角函数教育形态的重构

沈 威，曹广福



高中三角函数教育形态的重构

沈 威1，曹广福2

（1．惠州学院 数学与大数据学院，广东 惠州 516007；2．广州大学 数学与信息科学学院，广东 广州 510006）

三角函数的教育形态是能够变形式化的学术形态为学生从三角函数的数学思想和科学价值的高度再创造三角函数的内容．重构三角函数教育形态要挖掘三角学术形态的思想性与科学价值，根据数学思想和科学价值建构问题情境，提炼恰当的启发性问题，引导学生再创造三角函数的内容，揭示三角函数的数学思想与科学价值．

三角函数；教育形态；问题情境；重构

1 问题提出

张奠宙先生（以下简称：张先生）对数学的学术形态转化为教育形态作出了深刻论述，他认为变冰冷的美丽为火热的思考要把学术形态的数学返璞归真，从数学思想方法的高度把数学的形式化逻辑链条恢复为当初数学家发明创新时的火热思考[1]．换句话说，激发学生火热的数学思考要挖掘形成于学术形态数学中的深刻思想与科学价值，根据学生的数学现实与生活现实，重构教育形态的数学．

高中阶段的三角函数蕴含了丰富的数学思想，既是正弦定理、余弦定理的基础，还是高等数学中傅里叶级数、小波分析和泛函分析等学科的重要基础，可见三角函数在数学研究和科学研究中的重要地位与作用．就目前看，三角函数的相关研究主要表现为4大主题：（1）三角函数教科书的比较研究，按照时间发展的纵向顺序对一段时期内三角学教科书的三角函数的定义方式、图像、诱导公式等历史变迁作比较研究[2]，或者按照相同时间不同国家的横向关系，对两国或多国之间三角函数教科书的内容顺序、数学概念、核心定理、知识结构与呈现方式等作比较研究[3-4]；（2）三角函数内容理解的实证研究，选择数学专业大学生为被试编制问卷对高中三角函数内容深度进行研究[5]，或者选择高中学生为被试编制问卷研究高中学生对三角公式的理解情况[6]；（3）三角函数的教学设计分析，以国内三角函数教科书为对象，剖析其各教学环节存在的问题，根据其教学经验建构教学设计[7-8]；（4）三角函数教科书内容编写的研究，对三角函数相关定义的确定或对三角函数教科书内容体系改编的论证研究[1，9-10]．可以看出后两个主题和三角函数的教学或教育形态化有关系，但其研究内容很少从思想性与科学价值的高度探讨三角函数教育形态化．鉴于三角函数的深刻思想与科学价值对学生数学思维发展的重要意义，有必要对三角函数教育形态化深入研究．

研究主要围绕4个问题展开，首先，三角函数的深刻思想与科学价值是什么；其次，完善与建构已有三角函数教育形态化的理论框架与基本路径；第三，当前三角函数教科书存在哪些问题；第四，三角函数的教育形态的重构．

2 三角函数的深刻思想和科学价值

任何知识的产生与发展都是源于解决问题或自身逻辑发展的需要，知识蕴含的思想性与科学价值就体现在解决问题的过程中，三角函数的发展也不例外．虽然三角函数源于天文学，但在刻画物体振动、波的传播过程有着极大的科学价值．

2.1 三角函数的深刻思想

天文学发展初期，为农业编写历书需要测量与计算天体之间的距离，在测量与计算天体距离的过程中，逐渐抽象出以三角形为背景的静态几何问题，任意一个三角形问题都可以转化为直角三角形问题，也就是任意一个三角形问题都可以通过直角三角形来解决，所以测量与计算天体之间的距离就转化为研究直角三角形的问题，在求解直角三角形中，先贤们发现当固定一个锐角，其形成直角三角形的边之比是不变量，由此形成锐角三角函数的概念[11]．而由测量与计算天体之间距离的天文学逐渐独立成为天文学的一个分支——恒星天文学．由此可见，初中锐角三角函数蕴含着当固定一个锐角，其形成直角三角形的边之比是不变量的思想．

随着恒星天文学的发展，逐渐研究天体之间旋转运动关系，其中太阳、地球和月亮之间的旋转关系是最基本的三体模型．太阳、地球和月亮在公转与自转过程中，计算何时出现日全食，何时出现月全食，也就是研究如何把天体的旋转运动转换为直线运动，并探讨旋转的天体在旋转过程中所处的位置等，由此便形成高中三角函数的内容．可以看出，高中三角函数蕴含着旋转运动与直线运动的关系，质点在旋转过程中所处的位置等思想性．

三角函数在数学上逐渐发展出三角级数等．但是三角级数一直和恒星天文学形影不离，把三角级数运用于恒星天文学的研究，通过恒星天文学的研究促进了三角级数的发展．三角级数之所以在恒星天文学中有用，本质在于三角级数是周期函数，而天文现象大都呈周期性．开始运用三角级数于恒星天文学是要确定恒星在介于观测到的位置之间的位置，也就是偏微分方程中的插值问题，最早研究差值问题的是欧拉，他把已经得到的方法用到行星扰动理论中出现的一个函数上，得到函数的三角级数表示[13]．人民教育出版社出版的三角函数教科书也专门辟出篇幅讨论三角学与天文学的关系[14]．可以看出，三角函数与恒星天文学之间具有孪生性，没有恒星天文学就没有三角函数，如果三角函数得不到发展，恒星天文学就很难发展．换句话说，没有旋转运动与直线运动关系和质点在旋转运动所处位置等的研究，就无法揭示三角函数的深刻思想．

2.2 三角函数的科学价值

振动无处不在决定了波的无处不在．只要物体发生振动，就会形成波动，一切波动都是某种振动的传播过程．以波的形式传播的还有电波和光．波分为横波和纵波：像收音机、电视机、手机通信波，眼睛感受到的光、红外线等都属于电磁波，它们具有相同的物理性质，这些电磁波在真空中传播速度都是30万千米/秒，在电磁波中，电场和磁场的强度随时间变化，且它们的方向与波的传播方向垂直，这样的波叫作横波；像声音等利用空气等介质密度高低传播的，波的传播方向与振动方向相同的波叫作纵波．横波中电场和磁场在与前进方向垂直的上下方向上变化，用图形表示就是正弦函数的图象，纵波中密度的变化用图形表示出来，也是正弦函数，因此，不论是纵波还是横波，都可以利用正弦函数表示．由多个简单的波复合而成的复杂波形是傅里叶变换的基础，或者说研究简单波形合成复杂波的频率和强度的数学方法就是傅里叶变换．

傅里叶变换是傅里叶在研究“热传导法则”问题时开始用到的，他发现再复杂的现象也是由简单的现象组合在一起而形成的．受此启发，复杂的波也是由多个简单的波复合而成．1965年，根据离散傅里叶变换的奇、偶、虚、实等特性，也就是利用三角函数基本性质的组合，对离散傅里叶变换的算法进行改造，一种高效的傅里叶变换——快速傅里叶变换FFT（Fast Fourier Transform）被提出，傅里叶变换随着FFT和计算机的发展，很快在各领域获得应用．例如，医院使用的心电图仪器就是通过波的形状把病人心脏跳动直观表示出来，这就可以看出傅里叶变换广泛应用的范围了．傅里叶分析的核心是傅里叶定理，它是所有周期现象的核心．傅里叶把傅里叶定理扩展到非周期函数，把非周期函数看成周期函数的极限情况，这个想法对量子力学的发展具有重大影响．但是不管怎样，这都离不开正弦函数和余弦函数，正弦函数和余弦函数是三角级数和傅里叶分析的核心[12]．

3 高中三角函数教育形态化的理论框架与基本路径

高中三角函数的教学既不能直接把上述三角函数的深刻思想与科学价值直接告诉学生，也不能把三角函数的相关形式化概念陈述给学生，否则，学生只能机械记忆相关内容．这既不符合学生学习数学的心理特点，也违背了《普通高中数学课程标准（修订稿）》中倡导引导学生探究发现的教学理念[15]．只有恰当地把三角函数蕴含深刻思想与科学价值教育形态化，才能让三角函数知识及其深刻思想与科学价值在学生的数学认知结构中通透圆融的生成．

对于三角函数教育形态化，张先生给出如下建议[1]：

三角函数的教学，从静态的正弦定理、余弦定理到动态的周期变化、潮水涨落、弹簧及波的振动以及在轴上均匀旋转的轮子边缘上荧光点的运动等现象，把代数式、三角形、单位圆、投影、波、周期等离散的领域联系在一起．正是三角函数使它们形成一个有机整体，同时它们也是三角函数在不同侧面的反映．因此对于三角函数的教学必须通过再创造来恢复学生火热的思考，使之返璞归真．让三角函数丰满起来，才能把教科书上定义—公式—图像—性质—应用，这种冰冷的美丽变成学生丰富的联想，使学生在某一领域孤立学习的主题能迁移到另一领域中．

可以看出，张先生的三角函数教育形态化建议较为宏观，可操作性不强．例如，张先生指出“火热的思考应该提高到‘数学思想方法’的高度上来”，却未给出三角函数蕴含的数学思想与科学价值，也没有指出如何把三角函数的数学思想与科学价值“落脚”，供学生“火热的思考”．基于此，有必要完善张先生“三角函数教育形态化”的理论框架，明确其基本路径，不但使三角函数教育形态化具有可操作性，也为其它数学内容教育形态化或者评价教科书良莠带来启发．

张先生“数学学术形态与教育形态”理论来源于著名数学教育家弗赖登塔尔数学教育思想，发展三角函数教育形态化的理论框架与基本路径自然要以弗赖登塔尔数学教育思想的核心“数学教育是数学的再创造”为基础．张先生已经指出数学学术形态向教育形态转化要提高到数学思想方法的高度，所以要先挖掘三角函数的深刻思想与科学价值；其次，三角函数的深刻思想与科学价值要有适当的“落脚点”，才能为学生的再创造提供思想材料，这个“落脚点”便是建构问题情境；第三，有了问题情境，学生未必就能实现再创造，还要教师创造适当的启发性提示语启发学生的思维方向，再创造出三角函数的学术形态，揭示三角函数的深刻思想与科学价值．

其中，三角函数教育形态化的难点在于其问题情境的建构．除了上述指出建构三角函数的问题情境要蕴含三角函数深刻思想和科学价值，还要同时满足下面3个要素．在天文学中，地球绕着太阳转，月亮绕着地球转，计算什么时候出现日全食，什么时候出现月全食，就是太阳、地球、月亮在公转与自转过程中，计算任意一个时刻太阳、地球、月亮所处的位置，这就必须要建立任意角、弧度制、任意角的三角函数等概念，决定了三角函数问题情境背景要有统领性．在统领性的背景下建构问题情境能够随着知识不断生成而衍生出具有一定逻辑层次的新问题情境，即问题情境之间要具有连贯性．问题情境不但要蕴含三角函数的深刻思想和科学价值，还要联系学生的生活现实或数学现实，否则学生在理解问题情境背景本身花费大量时间，无法在有效时间内透过问题情境建构知识并揭示相应的数学思想与科学价值．即三角函数问题情境要同时具备4个要素：问题情境要蕴含三角函数深刻思想和科学价值；问题情境的背景具有统领性；问题情境之间具有连贯性；问题情境要联系学生的生活现实或数学现实．用图1直观表示三角函数学术形态向教育形态转化的理论框架和基本路径．

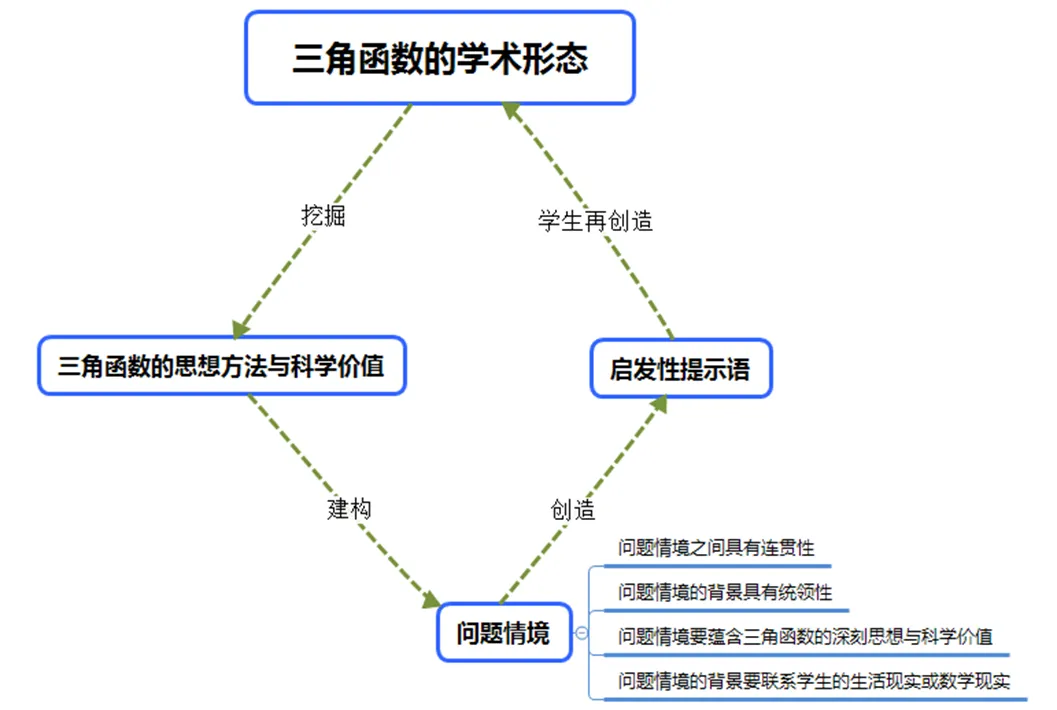
图1 三角函教育形态化的理论框架与基本路径

4 当前三角函数教科书的问题情境不真实且碎片化

依据三角函数教育形态化的理论框架与基本路径，可以发现三角函数教科书中存在诸多问题，下面以某高中数学教科书必修4“三角函数”一章的任意角、弧度制、任意角的三角函数和诱导公式的问题情境为例予以分析（见表1）[14]．

从问题情境蕴含三角函数思想性和科学价值的角度看，高中三角函数的深刻思想是旋转运动与直线运动的关系、质点在旋转过程中所处位置等，科学价值是三角函数刻画了物体振动、波的传播等周期现象．但是从这4节内容的问题情境看，均没有涉及旋转运动与直线运动关系、质点在旋转过程中所处位置的内容，也没有因需要刻画周期现象而创造新概念、新命题、新公式的内容．

从问题情境的背景统领性角度看，这4节内容问题情境的背景是手表快了或慢了、不同度量单位制、用平面直角坐标系中角的终边上的点的坐标表示锐角三角函数、三角函数的定义与圆的对称性，这些问题情境的背景各不相同，相互之间缺乏联系，不能相互统领，决定了无法把它们联系在一起视为一个具有统领性的问题情境背景．

从问题情境之间连贯性的角度看，这4节内容问题情境的背景没有统领性，决定了由这些背景形成的问题情境之间缺乏连贯性．例如，“弧度制”的问题情境是长度有不同的单位制、重量有不同的单位制，不同的单位制能给解决问题带来方便，所以要给角的度量“创造”一个单位制，但是该问题情境没有给出角度制解决问题带来不便的例子或问题，为何给角的度量“创造”一个新的单位制？新“创造”的单位制何以能给角的度量带来方便？仅仅因为长度有不同的单位制、重量有不同的单位制，要强制给角的度量增加一个单位制，似有“东施效颦”之嫌，存在逻辑矛盾．一个有逻辑矛盾的问题情境自然无法跟其它问题情境建立顺畅的连贯性．

表1 某高中数学教科书必修4“三角函数”一章创设的问题情境或问题

从问题情境联系学生的生活现实或数学现实角度看，“任意角”的问题情境以学生手表慢了5分钟需要校准为问题，考查学生如何校准手表，而后问学生“如果手表快了1.25小时如何校准，校准后，分针旋转了多少度”，从目前情况看，学生很少戴有时针/分针的机械表或者石英表，大都是表盘上直接显示时间数字的数码电子表，或者学生直接使用手机上的数码电子表，这类数码表精度高，不会出现快或慢的情况．也就是说学生在现实生活中很少接触到带有时针/分针的手表，从这个角度看“你的手表慢了5分钟，你是怎样将它校准的”的问题，无法获得预期的问题驱动效果，学生只需要回答“把数码电子表上的数字进行调整”即可．同样的，对于“假如你的手表快了1点25小时，你应当如何将它校准”，也是同样的回答．虽然学生能够计算出手表慢了5分钟分针旋转了多少度，但是该问题情境脱离了学生的生活现实，如果把“手表”改为“钟表”效果要好得多，因为大部分家庭都有有时针/分针的钟表．

仅在问题情境部分，教科书就存在诸多问题，这对把教科书当做教学和学习重要参考的教师和学生来说有严重的不利影响，有必要重构三角函数的教育形态，为三角函数的教学和学习提供新的视角．

5 三角函数教育形态重构框架

5.1 三角函数教育形态重构的基本思想

高中三角函数蕴含旋转运动和直线运动的关系、质点在旋转过程中所处位置的思想性，在刻画物体振动、波的传播过程的科学价值，应该在重构的问题情境中揭示．决定了创设的问题情境既要揭示三角函数的思想性，还要能体现三角函数的科学价值．天文学背景比较复杂，且超出学生的生活现实与数学现实，不宜直接引入揭示高中三角函数的深刻思想与科学价值，需要把问题情境的背景更换并作适当简化．根据三角函数建构问题情境的四要素，从高中三角函数蕴含的深刻思想与科学价值和学生生活现实出发，以汽车车轮与里程表系统为背景建构问题情境满足要求．汽车车轮与里程表之间的关系蕴含了旋转运动和直线运动的关系、质点在旋转过程中所处位置的思想性，车轮上质点随汽车向前平移过程中相对于车轴留下的轨迹，直观揭示了波的传播过程，既满足学生的生活现实和数学现实，还能同时揭示三角函数的思想性和科学价值．从这个意义上说，以汽车车轮与里程表系统之间关系作为统领高中三角函数的问题情境比较恰当．

下面以任意角、弧度制、任意角的三角函数和诱导公式4节内容为例，把汽车车轮与里程表之间关系进一步细化为4个子问题情境（图2），不同问题情境揭不同知识的数学本质．

图2 高中三角函数教育形态重构思路结构

5.2 任意角教育形态的重构

要揭示“揭示旋转运动和直线运动的关系、质点在旋转过程中所处位置”的思想，任意角的问题情境可以建构为：

在天文学中，计算何时出现日全食、月全食，需要计算太阳、地球和月亮所在的位置，这是一个有趣而又复杂的问题，且太阳、地球和月亮位置关系的原理在我们生活也很常见．例如，我们都坐过汽车，汽车里程表记录了汽车所行驶的路程，里程表数和车轮就蕴含了太阳、地球和月亮位置关系的原理（见图3），可以通过研究汽车里程表与车轮间的关系，间接研究太阳、地球和月亮之间的关系原理．

如果车轮的半径是0.3米，如何计算里程表上的数据？如果车轮的半径是0.25米，如何计算里程表上的数据？如果车轮的半径是1呢？如何计算里程表上的数据？其中变的是什么？不变的是什么？你发现了什么规律？

图3 汽车里程表和车轮

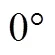
启发性问题1：如何计算汽车里程表的数据？能不能把问题情境抽象为数学问题（图4）？

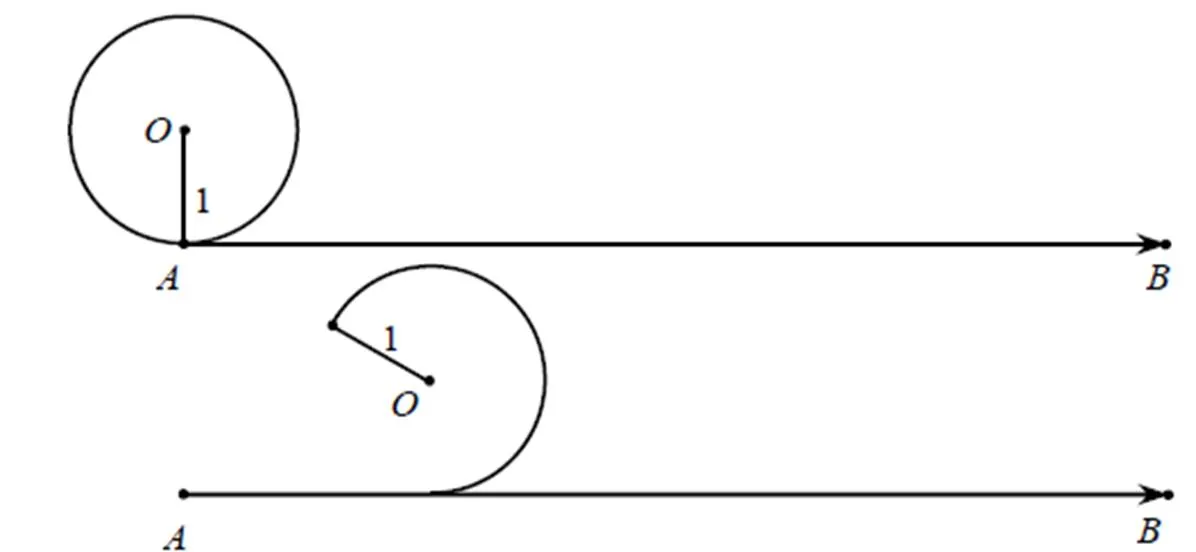
图4 问题情境抽象

评析：引导学生阅读材料，把问题情境数学化为具体的数学问题，培养了学生的数学阅读能力和抽象能力，体会“旋转运动和直线运动关系”的思想．在此基础上启发学生认识到解决这个问题，要准确刻画车轮上一点的旋转，不仅要定义角，还要知道该点旋转的度数、方向，当车轮旋转超过一周时要推广角的范围，需要建构角的动态定义，根据角的旋转方向定义正角、负角、零角，推广角的范围等都是因为解决问题的需要而必然的结果．

启发性问题2：能不能从动态的、旋转的视角对角作出定义？

启发性问题3：角的始边是如何旋转的？如何刻画？

启发性问题4：当角的始边旋转超过一周，如何刻画？

评析：定义动态的角、正角、负角、零角，推广角的范围后，还不能计算汽车里程表的数据，因为在刻画车轮旋转量这个问题上存在争议，不同学生选择角的始边可能不一样，给研究问题带来一定的复杂性，有必要统一角的始边，即角的始边标准化．

启发性问题5：不同学生规定角的始边可能不同，这会给研究问题带来什么影响？如何解决？

评析：至此，学生再创造了诸多概念，规定了角始边的方向，而创造概念的目的是为了解决最初的问题，还需要引导学生回到最初问题上．

启发性问题6：如何计算汽车里程表的数据？其中变的是什么？不变的是什么？你发现了什么规律？

评析：通过问题解决，引导学生认识角的终边在周而复始的旋转，初步体验“周期性”思想．

5.3 弧度制教育形态的重构

对于说法一，这种说法比较牵强，原因在于函数定义历经数次发展演变，均是因为原有函数定义不能涵盖其所有对象，必须要发展以适应于所有的具体函数．而说法一则把函数定义视为一成不变的，所有具体函数必须要满足函数定义，如果不满足，则要自我调整，相对于函数概念的发展历程，无法作为三角函数引入弧度制的必然选择．对于说法二，前面已经分析这种说法的矛盾性．对于说法三，弧度制简化了计算公式，人们认可这种说法，简化公式一直是数学的追求，为计算带来极大的便捷性，在天文学中计算日全食、月全食时，简化公式就是优化算法，加快计算速度，这在计算机出现之前显得尤为需要，同时，弧度制把旋转运动形成的弧长和直线运动形成的线段建立一一对应关系，把角与弧长建立等价关系，为旋转运动转化为直线运动建立桥梁，体现了其重要科学价值．这在汽车里程表的数据计算上，简化角度制下的弧长计算公式，在汽车车轮与里程表系统为背景的问题情境中依然显得非常必要与自然．

获得弧度制之后的内容，例如，弧度制与角度制之间的比较、互化，给弧度制下的角规定方向，弧度制下角的集合与实数集之间建立一一对应关系等，人民教育出版社等出版的《普通高中课程标准试验教科书·必修4》都已经给出比较好的参考，因此，这里仅探讨弧度制的生成．

弧度制的问题情境可以建构为：

在任意角部分，探究了汽车里程表数据与车轮之间的关系，你们是如何计算的？计算的式子是否复杂？观察式子，能不能找出规律，简化计算过程？

评析：引导学生把注意力放在已有的式子上，观察式子的结构，找出式子不变的部分，根据不变性对其作出新的规定与定义．

启发性问题3：在弧度制下，汽车里程表数据的计算公式是什么？在弧度制下，还有哪些公式还可以简化？

评析：因简化公式的需要，建构了弧度、弧度制等，这些概念是为解决问题服务的，启发性问题3则是引导学生回到并解决问题情境的问题．弧度制的形成过程主要培养了学生的纵向思维，而“在弧度制下，还有哪些公式还可以简化”则是培养学生横向思维，弧长公式、扇形面积公式等均和圆心角有关系，这里放弃相关教科书以例题证明的形式给出，而是以问题的形式提出，培养了学生触类旁通、举一反三的横向思维．

5.4 任意角的三角函数教育形态的重构

任意角的三角函数在三角学中具有重要地位，在教学中，引导学生认识到因为研究问题的需要而建构任意角三角函数历来都是教学的重点和难点．这里则把注意力放在此处，当引导学生认识到因为研究问题的需要而建构任意角三角函数之后，也就是定义任意角的三角函数、讨论三角函数在平面直角坐标系四个象限的符号等，相关教科书给出了较好的参考，这里不再赘述．

问题情境：因为探究何时出现日全食、何时出现月全食，我们研究了汽车里程表系统与车轮之间的关系，获得了任意角和弧度制的概念，现在运用任意角和弧度制能否计算何时出现日全食、何时出现月全食了？还不可以，仅有任意角和弧度制还不能确定任一时刻太阳、地球和月亮的位置，但是他们却为我们进一步研究奠定了坚实的基础．太阳、地球和月亮在公转时都是在做近似圆周运动，确定任一时刻太阳、地球和月亮的位置，就相当于车轮上一质点在任意角度所处的位置，如果把车轮半径视为单位1，你能用数学方法刻画车轮上一质点所处的位置吗（图5）？

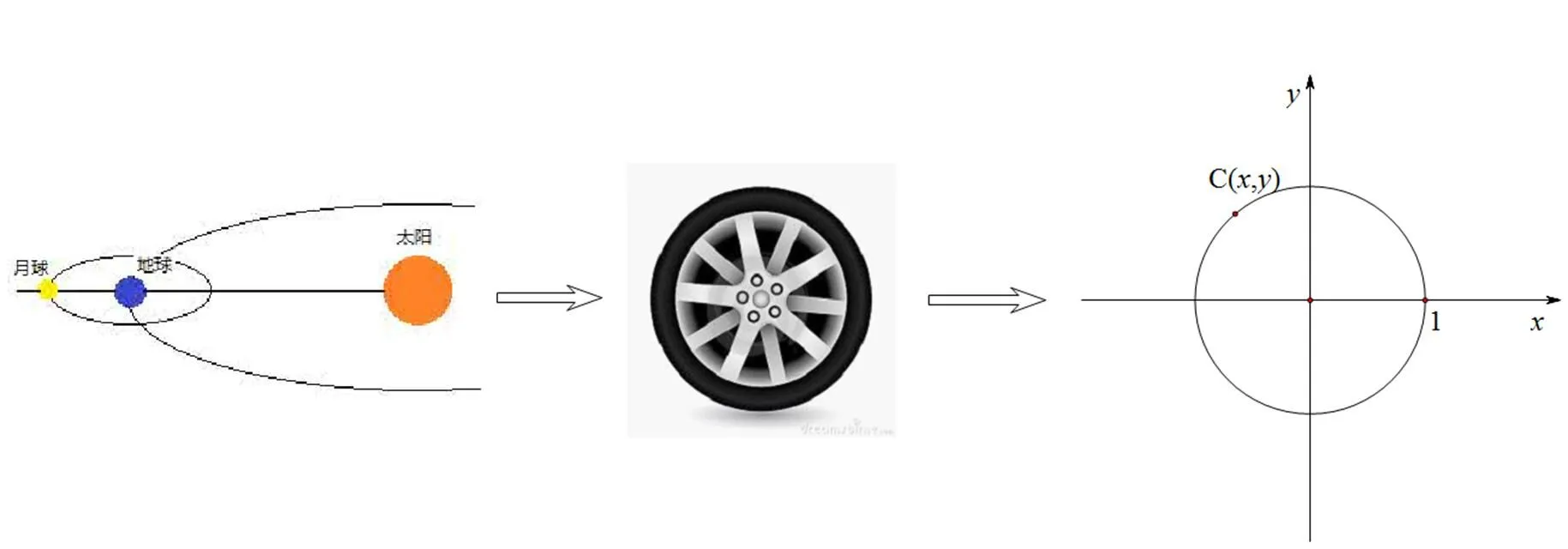
图5 数学方法刻画车轮质点位置

评析：汽车通过车轮旋转驱动汽车向前或向后运动，把车轮上一个点视为一个质点，它绕着车轴旋转，车轮旋转使得车轮作圆周运动推动汽车向前做平移运动，也就是旋转运动转变为直线运动，汽车向前平移过程中，车轮上质点所处位置在时刻发生变化，本质上是一个质点绕着一个正在做直线运动的质点做旋转运动的问题．把这个情境数学化，就是车轮上质点横坐标是汽车平移的位移，而纵坐标就是汽车平移位移的正弦值．当汽车在行驶过程中，车轮的不断旋转使得汽车平移的自变量在逐渐不断增加或减小，超出了锐角的范围，因此需要定义任意角的正弦函数．同时，在汽车向前平移过程中，质点绕着车轮中心旋转的角度在不断增加，如果问题指向质点绕车轮中心的相对位置是什么，这就需要同时定义任意角的正弦函数和余弦函数．由此，建构任意角三角函数概念的必要性就被清楚揭示出来．

启发性问题1：车轮上一质点绕车轴旋转有什么特点？旋转形成的轨迹是什么？

评析：根据问题情境，启发学生认识到车轮上一质点作匀速圆周运动，呈周期性变化，旋转形成的轨迹是圆周，这为下面研究任意角三角函数提供抽象基础．当学生把单位圆抽象出来后，便可以引导学生建构任意角三角函数的过程了．虽然已经获得点的轨迹是单位圆，但是如何刻画点的横坐标和纵坐标还存在突破的空间，特别是横、纵坐标的自变量．人民教育出版社等教科书均是直接给出(sin, cos)，自变量就是角的终边旋转量，这里有一个疑问，即虽然角的终边旋转量为，那么的横、纵坐标的自变量一定是吗？为了引导学生对这个问题的本质认识，自然引出启发性问题2．

启发性问题2：现在假设车轮中心在轴上，车轮半径为1，视车轮所在的圆上一质点与平面直角坐标系原点重合．当汽车行驶时，质点在平面直角坐标系中的坐标(,)如何表示（图6—图8）？

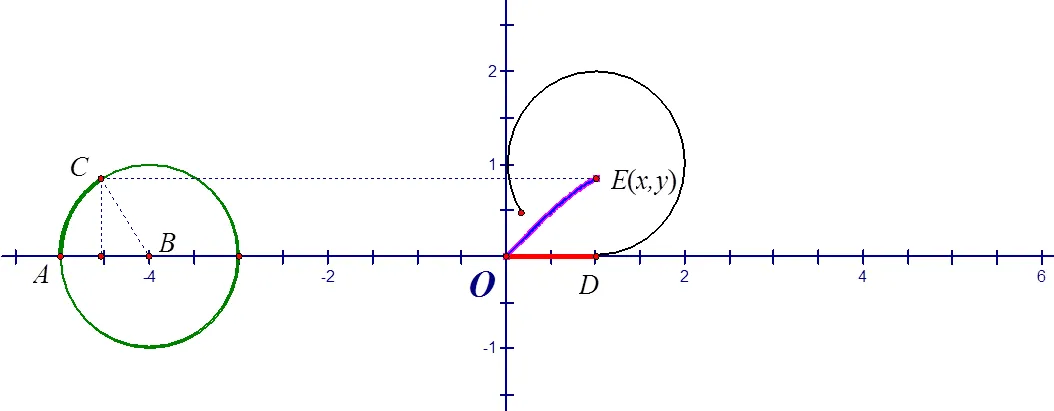
图6 E点坐标表示（一）

图7 E点坐标表示（二）

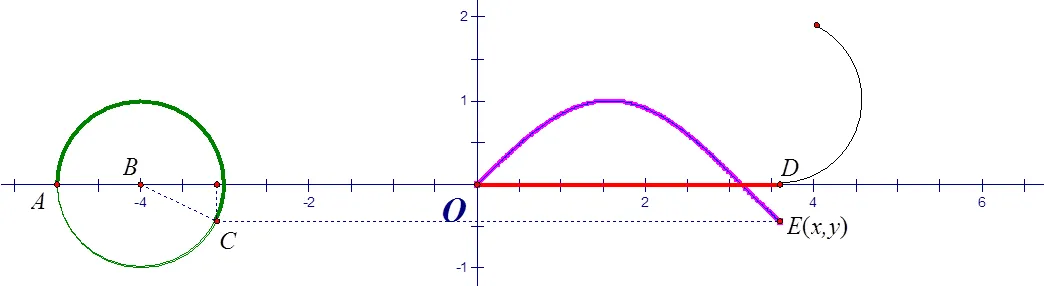
图8 E点坐标表示（三）

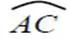
启发性问题3：质点绕车轴旋转，它相对于车轴的位置如何刻画（图9）？

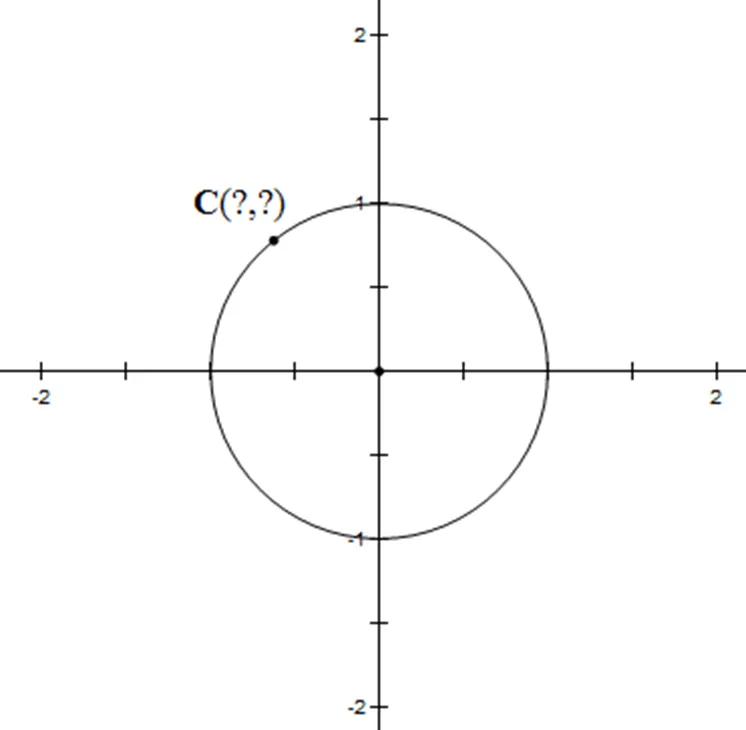
图9 质点C相对于车轴的位置

评析：启发性问题2揭示了点纵坐标及其自变量之间的关系，启发性问题3则把研究范围扩展到点的横、纵坐标，学生有了纵坐标的研究经验，继续研究横坐标则会顺利些．根据点所在的位置，引导学生认识到需要定义任意角的三角函数．

启发性问题4：如何定义任意角的三角函数？

5.5 诱导公式教育形态的重构

为了计算何时出现日全食、月全食，获得了任意角的三角函数，它刻画了圆周上一质点在任意时刻所在的位置，但相应位置三角函数值的求解还未解决，因此，探究求解任意角的三角函数值的方法就是该节内容的主要任务．该节继续并充分用好“汽车车轮上质点坐标”这个物理背景，让学生在对这个物理背景有充足认识的前提下继续深挖该物理背景，从而获得诱导公式，由此解决“汽车车轮上质点坐标”问题．诱导公式的实质是“揭示了任意角三角函数与锐角三角函数之间的关系”，揭示了“任意角三角函数与锐角三角函数之间的关系”，从而发现“任意角的三角函数值可以用0°~90°以内角的三角函数值求得”，这正是在计算机发明之前，诱导公式的美妙之处、价值所在，这也才是诱导公式的本质之所在．

问题情境：我们在上一节已经能够表征出汽车车轮上质点的坐标，即(, sin)，但如何求出任意角的正弦函数sin的值（图10）？

评析：由图10能够看出点坐标(, sin)“周而复始”地出现，并相差一个圆周的整数倍，即相差2π的(ÎZ)倍．若令∠=，当Î[0, 2π]时，而汽车向前平移了时，且=2π+，其对应的纵坐标相等，则获得公式sin(2π+)=sin．结合相对于车轮中心并绕车轮中心旋转的汽车车轮上质点的坐标看（图11），若令Î[0, 2π]时，当质点旋转了时，且=2π+，其对应的横坐标、纵坐标相等，则获得公式一：sin(2π+)=sin，cos(2π+)=cos，tan(2π+)=tan(ÎZ)．即终边相同的角的同一三角函数值相等．利用公式一，可以把求任意角的三角函数值，转化为求0~2π角的三角函数值．

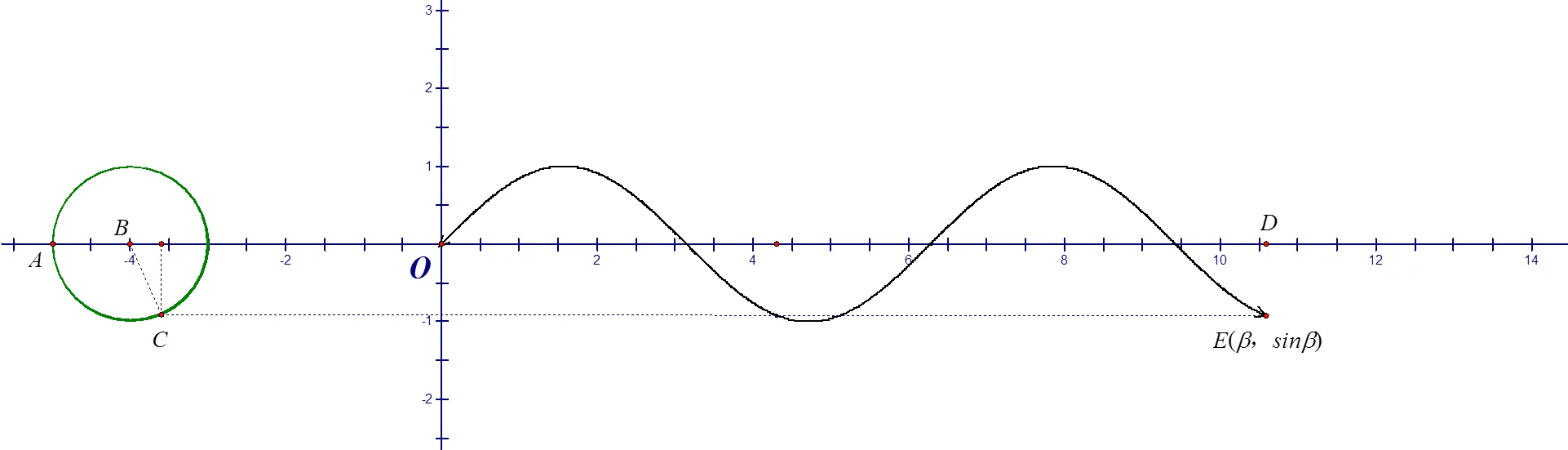
图10 任意角的正弦函数值

启发性问题1：虽然公式一能够把任意角的三角函数值转化到求0~2π角的三角函数值，如何求0~2π角的三角函数值？你会求哪些角的三角函数值（图12）？

评析：引导学生根据初中锐角三角函数知识求锐角三角函数值，根据“终边相同的角的三角函数值相等”，若任意角与锐角的终边相同，即角和之间相差2π倍，有=2π+(ÎZ)，那么它们的三角函数值相等．

启发性问题2：公式一的作用是什么？根据公式一的获得过程，你能获得哪些结论？

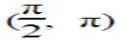
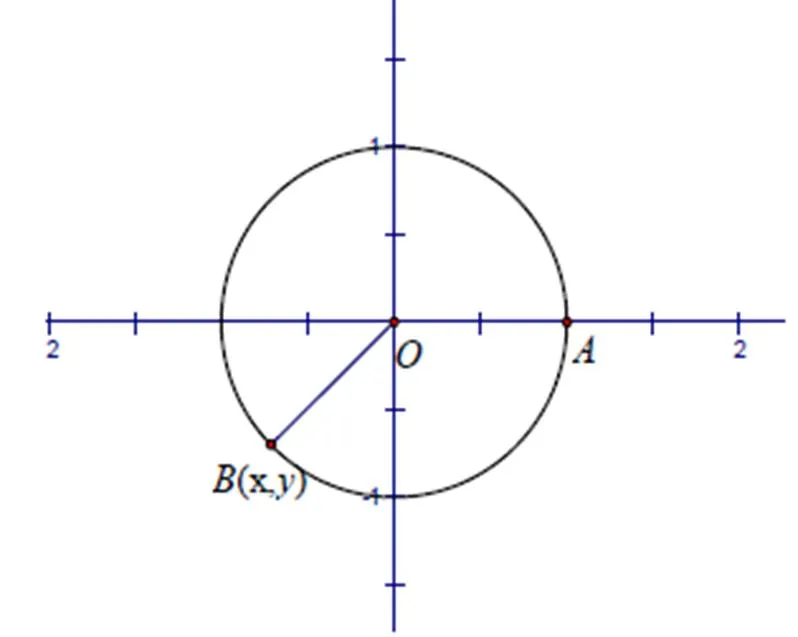
图11 质点B坐标

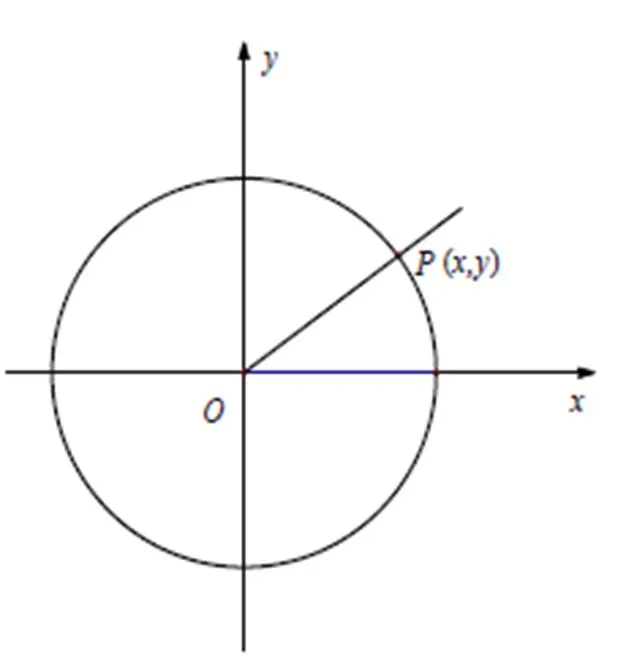
图12 求三角函数值（一）

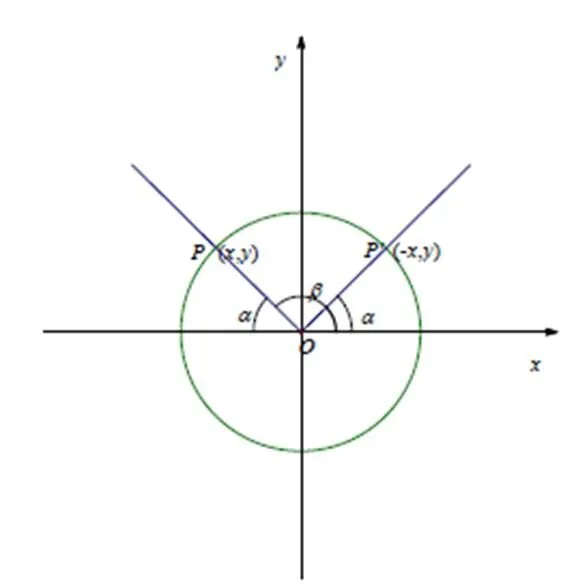
图13 求三角函数值（二）

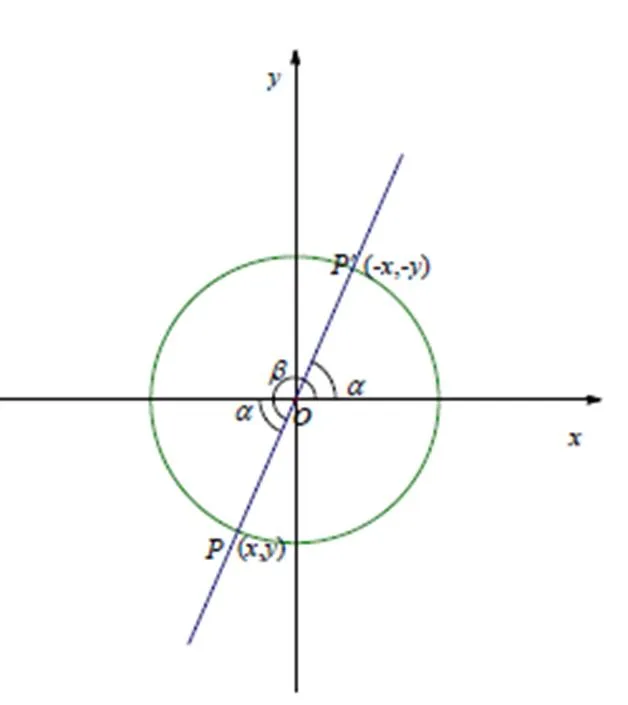
图14 求三角函数值（三）

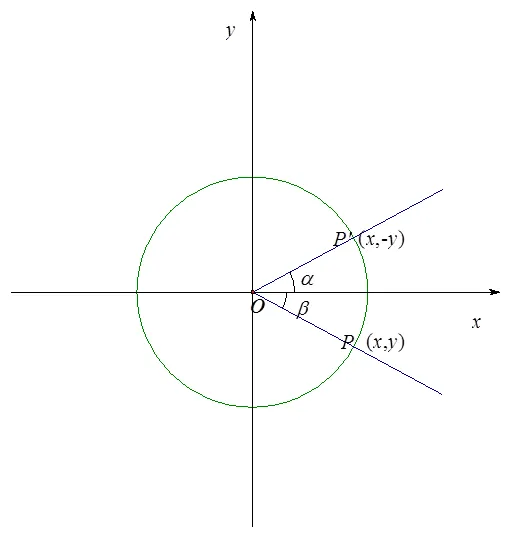
图15 求三角函数值（四）

评析：对角终边对称关系的定位在为解决问题的需要而不得不引入，在该节之初所提出的问题中没有涉及角的终边的对称关系，因为还不知道要把角的终边的对称关系引进来．作角的终边关于坐标轴对称、关于原点对称是获得把未知问题转化为已知问题的工具，何时使用工具全看问题解决本身的需要，而不是在没有问题之前，就把工具放在面前，面对工具思索这些研究工具可以做什么，这不符合数学研究规律．

[1] 张奠宙，王振辉．关于数学的学术形态与教育形态[J]．数学教育学报，2002，11（2）：1-4．

[2] 刘冰楠，代钦．民国时期国人自编三角学教科书中“三角函数”变迁[J]．数学教育学报，2015，24（3）：81-85．

[3] 陈月兰．中日三角比内容比较[J]．数学教育学报，2013，22（3）：1-4．

[4] 朱少卿，胡典顺．中美两套教科书中三角函数的比较研究[J]．数学通报，2014，53（10）：46-50．

[5] 佘丹．高中三角函数内容深度的实证研究[J]．数学教育学报，2014，23（6）：85-87．

[6] 何忆捷，彭刚．高中生三角公式理解的实证研究[J]．数学教育学报，2014，23（1）：51-56．

[7] 黄晓琳，李祎．“任意角的三角函数”教学析惑与设计探微[J]．数学通报，2014，53（11）：22-25．

[8] 渠东剑．追求自然连贯的数学教学过程[J]．数学通报，2014，53（12）：12-16．

[9] 章建跃．为什么用单位圆上点的坐标定义任意角的三角函数[J]．数学通报，2007，46（1）：15-18．

[10] 张景中．三角下放全局皆活[J]．数学通报，2007，46（1）：1-4．

[11] 容建湘．恒星天文学[M]．北京：高等教育出版社，1986：1-50．

[12] 马奥尔．三角之美：边边角角的趣事[M]．北京：人民邮电出版社，2010：111．

[13] 克莱因 M．古今数学思想（第三册）[M]．上海：上海科学技术出版社，2014：182．

[14] 课程教科书研究所．普通高中课程标准试验教科书A版·数学（必修4）[M]．北京：人民教育出版社，2007：2-27．

[15] 洪燕君，周九诗，王尚志，等．《普通高中数学课程标准（修订稿）》的意见征询——访谈张奠宙先生[J]．数学教育学报，2015，24（3）：35-39．

[16] 章建跃．如何使学生理解三角函数概念[J]．中小学数学（高中版），2017（6）：66．

[责任编校：周学智]

Reconstruction of the Education Form of Trigonometric in Senior High School

SHEN Wei1, CAO Guang-fu2

(1. College of Mathematics and Big-Data Science, Huizhou University, Guangdong Huizhou 516007, China;2. School of Mathematics & Information Science, Guangzhou University, Guangdong Guangzhou 510006, China)

The education form of trigonometric function was to change the formalized academic form into the content of trigonometric function recreated by the students highly from the mathematical idea and the scientific value. Reconstruction of the education form of trigonometric function needed to explore the ideological content and scientific value of the academic form of triangle, construct problem situations according to the mathematical idea and scientific value, summarize proper heuristic questions, and guide the students to recreate the content of trigonometric function, to reveal the mathematical idea and scientific value of trigonometric function.

trigonometric; educational form; problem situation; reconstruction

G632.0

A

1004–9894（2017）06–0014–08

沈威，曹广福．高中三角函数教育形态的重构[J]．数学教育学报，2017，26（6）：14-21．

2017–06–02

广东省“特支计划”教学名师项目——问题驱动的数学课堂教学；广东省高等教育教学改革项目——卓越视野下职前数学教师教学能力培养模式研究；惠州学院优秀青年培育项目——数学教师核心素养研究

沈威（1982—），男，安徽灵璧人，副教授，博士，主要从事数学课程与教学论研究．