学生知识经验对分离元素策略的影响
2017-12-22陈鸥昊连四清
佘 岩,陈鸥昊,连四清
学生知识经验对分离元素策略的影响
佘 岩1,陈鸥昊2,3,连四清1
(1.首都师范大学 数学科学学院,北京 100048;2.新南威尔士大学 教育学院,澳大利亚 2052;3.南洋理工大学 国立教育学院,新加坡 637616)
分离元素策略是通过分割完整学习材料从而降低元素交互度,进而降低内在负荷的教学设计策略.研究考察了学生知识经验对分离元素策略的影响.实验结果表明:无论远近迁移,不同水平学生在呈现有无使用分离元素策略的学习材料时交互作用均显著.其中,学困生呈现分离元素策略材料解决远近迁移问题均显著好于呈现无策略材料;学优生呈现两种学习材料对解决远近迁移问题无显著差异.这说明,分离元素策略可作为有效的引导学困生学习的策略.
认知负荷理论;内在负荷;分离元素策略;学生知识经验
1 问题提出
工作记忆是提供临时存储和加工信息的容量有限的记忆系统[1].人们所完成的任何认知活动均需要工作记忆的参与,但其容量的有限性又制约着人们完成复杂的认知任务.Sweller等人基于工作记忆系统的容量有限性把认知负荷定义为:需要完成的任务对工作记忆系统中总资源的需求[2].因此,如何控制认知负荷总量,使其不超出工作记忆总容量是认知任务能否完成的关键.
在认知负荷理论中,将发生在学习过程中的认知负荷分为3类:表示学习材料本身复杂程度的内在负荷,由教学设计等外在因素引起的外在负荷以及在图式获得和自动化过程中产生的相关认知负荷[3].与相关认知负荷不同,内在负荷或外在负荷的增加会导致工作记忆系统超负荷,影响相应图式的建构.因此,研究者提出多种降低外在负荷的策略(即认知负荷效应)以便学习者将心理资源投入到与图式建构、自动化相关的活动上,这些策略已被证实能够促进图式的获得.例如:解决复杂任务,即学习具有高内在负荷的材料时,提供有详细解答步骤和答案的样例学习更有利于获得相应图式,即样例效应[4-9].
作为内在负荷的评价指标,元素交互度是指某一知识中包含的独立信息的交互程度[10].元素交互度与学习者的已有知识经验密切相关.对于某特定领域内的一个特定知识,已具有相应知识的学习者可将从长时记忆中提取出的相应图式作为一个元素在工作记忆中处理,因此元素交互度较低,即该学习者学习的是低内在负荷材料.反之,知识经验少的学习者无特定的图式可以提取,故需要在工作记忆中单个处理涉及的元素及其内在关系,所以元素交互度较高,由此造成此材料为高内在负荷的学习材料[11].总之,具有不同知识经验的学习者在特定材料下的元素交互度不同,从而影响内在负荷的高低.
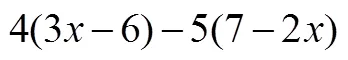
然而,上述基于分离元素策略的研究中,研究者均是以样例学习为研究范式,证实了分离元素策略的有效性.但在实际教学过程中,往往希望在呈现完整解答过程(样例学习)之前,学生能够独立解决问题.若学生不具备独立解决问题的知识经验或水平(被试知识经验少),往往希望能够给予“合理提示”引导学生独立解决.根据前人研究结论可以猜想,分离元素策略可以作为一种引导学生解决问题的方式.据此,研究拟呈现无解答过程的题目,考察分离元素策略的有效性.同时,亦考察分离元素策略是否受到学生知识经验的影响.
目前,大量研究已考察了样例迁移的影响,得到呈现不同数量、不同编码方式样例对不同迁移水平存在差异[19-22].Ayres(2013)的研究虽然将测试材料分为远近迁移,但并未说明其迁移程度的界定方法.连四清等人认为,可以用纯数学问题的“解题步骤”、“特征”刻画学习材料与测试材料的相似程度[23].Ayres选用的去括号问题正是一类纯数学问题,其区分远近迁移的两个指标——所含未知数的个数和待展开括号的个数影响了解决问题的步骤和特征.因此,Ayres远近迁移测试材料的设计具有理论依据.研究亦采用同样的界定方式考察分离元素策略对远近迁移的影响.
2 研究方法
实验设计:采用2(问题呈现方式:分离元素策略,无策略)´2(学生类型:学优生,学困生)析因实验设计.其中,问题呈现方式和学生类型均为被试间变量,近迁移和远迁移的成绩为因变量.
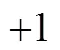
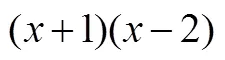
程序:实验分为学习阶段和测试阶段.学习阶段分为两个子阶段,在第一个子阶段中,分离元素策略组需完成第一、二页学习材料的题目,无策略组完成第一页学习材料的题目.在第二个子阶段中,全体被试完成剩余一页学习材料.实验流程如下:被试被随机分配两种学习材料,并用10分钟完成第一子阶段的学习.10分钟后回收第一子阶段材料并再用10分钟完成第二子阶段材料的学习.随后回收第二子阶段材料并发放测试材料.被试有10分钟时间完成测试材料.所有阶段材料均不能回顾或提前学习.
评分标准:去括号时,若某两个数字(字母)对应相乘结果错误扣1分.近迁移总分8分,远迁移总分20分.
3 结果
对实验数据用PASW 18.0 for windows进行2(问题呈现方式:分离元素策略,无策略)´2(学生类型:学优生,学困生)双因素方差分析.
3.1 对近迁移成绩的分析
近迁移成绩的描述性统计结果如表1所示.

表1 不同问题呈现方式与不同能力被试的近迁移成绩

3.2 对远迁移成绩的分析
远迁移成绩的描述性统计结果如表2所示.

表2 不同问题呈现方式与不同能力被试的远迁移成绩
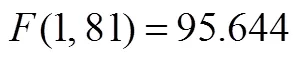
4 讨论
4.1 不同学生类型对整式乘法学习存在显著差异
学习者虽已不同程度掌握了整式去括号的运算原理,但他们的长时记忆中均未存储完整的多项式乘法图式.相较于学困生而言,学优生能将单项式乘多项式的运算原理迁移到多项式乘法的问题中,即:能独立建构多项式乘法运算的图式.而对于学困生,特别是学习无策略材料的学困生则很难独立完成此种复杂的心理加工,内在负荷高.因此,学优生在近迁移成绩上显著好于学困生.对于远迁移测试,虽然其材料中题目的原理与学习材料相同.但题目中解题步骤的改变亦干扰了学生对多项式乘法原有图式的识别和匹配,亦增加了学习者的内在负荷.从实验结果看,这种改变对学困生的影响更大.
4.2 学生类型与问题呈现方式交互影响近远迁移成绩
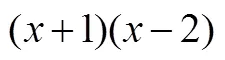
5 结论
此实验结果与Ayres以样例为背景,采用分离元素策略所得结果一致[16].但此实验,进一步推广了分离元素策略的应用,即:分离元素策略可作为一种引导学困生完成单纯问题解决的有效策略.特别是分离元素策略能够帮助学困生自主生成问题解决的图式,并对解决解题步骤、题目特征不同的远迁移问题具有指导作用[25-31].但对于学优生而言,分离元素策略并未有效促进其学习.
在教学中教师可依据分离元素策略的原理,将复杂的学习材料分离成元素交互程度低的多个子材料,依次将其呈现给学生,以降低材料的内在交互度,使得学生达到更好的学习效果.
研究在真实的教学环境中进行,因此受课时安排,近远迁移测试题目较少,现有题目虽已达到较好地信度,但在未来的研究中拟增加测试题目的数量,以达到更好的测试效果.此外,研究仍选取代数知识作为背景,而对于更复杂的几何问题,能否采用分离元素策略引导学生自主学习可作为未来进一步的研究方向.
[1] BADDELEY A D. Working memory [J]. Science, 1992, 255 (5 044): 556-559.
[2] SWELLER J. Cognitive load during problem solving: effects on learning [J]. Cognitive Science. 1988, 12(2): 257-285.
[3] SWELLER J. Elementary interactivity and intrinsic, extraneous and germane cognitive load [J]. Education Psychology Review, 2010 (22): 123-138.
[4] SWELLER J, COOPER G A. The use of worked examples as substitute for problem solving in learning algebra [J]. Cognition and Instruction, 1985, 2(1): 59-89.
[5] COOPER G A, SWELLER J. Effects of worked examples, example-problem, and problem-solving transfer [J]. Journal of Educational Psychology, 1987, 79(4): 347-362.
[6] RENKL A. Learning from worked-out examples: a study on individual differences [J]. Cognitive science, 1997, 21(1): 1-29.
[7] ATKINSON R K, DERRY S J, RENKL A, et al. Learning from examples: instructional principles from the worked examples research [J]. Review of Educational Research, 2000 (70): 181-214.
[8] SCHWONKE R, RENKL A, KRIEG C, et al. The worked-example effect: not an artifact of lousy control conditions [J]. Computers in Human Behavior, 2009 (25): 258-266.
[9] SWELLER J, AYRES P, KALYUGA S. Cognitive load theory [M]. New York, IL: Springer, 2011: 95.
[10] KALYUGA S, CHANDLER P, SWELLER J. Learner experience and efficiency of instructional guidance [J]. Education Psychology, 2001, 21(1): 5-23.
[11] SWELLER J. Cognitive load theory, learning difficulty, and instructional design [J]. Learning and Instruction, 1994 (4): 295-312.
[12] MAYER R E, MATHIAS A, WETZELL K. Fostering understanding of multimedia messages through pre-training: evidence for a two-stage theory of mental model construction [J]. Journal of Experimental Psychology: Applied, 2002, 8(3): 147-154.
[13] VAN MERRRIËNBOER J J G, CLARK R E, DE CROOCK M B M. Blueprints for complex learning: the 4C/ID-Model [J]. Educational Technology, Research & Development, 2002 (50): 39-64.
[14] CATRAMBONE R. The subgoal learning model: creating better examples so that students can solve novel problems [J]. Journal of Experimental Psychology: General, 1998 (127): 355-376.
[15] POLLOCK E, CHANDLER P, SWELLER J. Assimilating complex information [J]. Learning and Instruction, 2002 (12): 61-86.
[16] AYRES P. Impact of reducing intrinsic cognitive load on learning in a mathematical domain [J]. Applied Cognitive Psychology, 2006 (20): 287-298.
[17] AYRES P. Can the isolated-elements strategy be improved by targeting points of high cognitive for additional practice [J] Learning and Instruction, 2013 (23): 115-124.
[18] 甘卫群,刘万伦.样例的概念属性呈现方式对初一学生分式概念学习的影响[J].数学教育学报,2015,24(6):68-72.
[19] 邢强,莫雷.多重样例的变异性和编码对迁移影响的实验研究[J].心理科学,2005,28(6):1 382-1 387.
[20] 宁宁,喻平.多重变异性数学样例对迁移影响的初步研究[J].数学教育学报,2010,19(6):50-52.
[21] 徐碧波,林崇德,杨永宁.样例顺序和解释方式对问题解决迁移的影响[J].心理科学,2010,33(2):278-281.
[22] 连四清,曾辉.自我解释对等差数列概念和通项公式远近迁移的影响[J].数学教育学报,2011,20(2):23-25.
[23] 连四清,佘岩,王欣.一元二次不等式的特征对其解法迁移的影响[J].数学教育学报,2014,23(2):57-59.
[24] KALYUGA S, AYRES P, CHANDLER P, et al. The expertise reversal effect [J]. Educational Psychologist, 2003, 38(1): 23-31.
[25] 佘岩,徐玲玲.整式运算认知诊断初探[J].数学教育学报,2017,26(3):49-52.
[26] 任旭,夏小刚.问题情境的创设:基于思维发展的理解[J].数学教育学报,2017,26(4):15-18.
[27] 史淑莉.数学素养视阈下初高中数学衔接问题研究[J].数学教育学报,2017,26(4):30-33.
[28] 刘荣玄,朱少平.概念图引导型构图题的研究与实践[J].数学教育学报,2017,26(2):86-88.
[29] 李昌官.数学抽象及其教学[J].数学教育学报,2017,26(4):61-64.
[30] 单妍炎,黄秦安.解释学观照下数学对话的内涵与特征[J].数学教育学报,2017,26(3):98-100.
[31] 聂晓颖,黄秦安.论数学课堂文化的内涵与模式及对培养数学核心素养的价值[J].数学教育学报,2017,26(2):71-74.
[责任编校:周学智]
Effect of Learners’ Expertise on Isolated-Element Strategy
SHE Yan1, CHEN Ou-hao2, 3, LIAN Si-qing1
(1. School of Mathematical Sciences Capital Normal University, Beijing 100048, China;2. School of Education, University of New South Wales, 2052, Australia;3. National Institute of Education, Nanyang Technological University, Singapore, 637616)
The isolated-element strategy was an instructional method used to reduce the levels of intrinsic load via reducing the levels of element interactivity. This study investigated the effect of learners’ expertise on isolated-element strategy. The results confirmed that the isolated tasks were superior to non-isolated tasks for low expertise learners on both similar and far transfer tests, but no significant results for more knowledgeable learners. Therefore, presenting isolated tasks was an effective strategy for low expertise learners.
cognitive load theory; intrinsic load; isolated-element strategy; learners’ expertise
G632
A
1004–9894(2017)06–0056–04
佘岩,陈鸥昊,连四清.学生知识经验对分离元素策略的影响[J].数学教育学报,2017,26(6):56-59.
2017–10–20
佘岩(1990—),女,北京人,博士,主要从事中小学数学教育研究
