二阶常系数线性非齐次微分方程的一些解法

李迎娣

(黄河科技学院 国际学院，河南 郑州,450000)

二阶常系数线性非齐次微分方程的一些解法

李迎娣

(黄河科技学院 国际学院，河南 郑州,450000)

我们探讨了如何求二阶常系数线性齐次微分方程的解，利用通解的结构和自由项的形式来求解；利用通解公式来求解。

二阶常系数线性微分方程；自由项；特征方程；通解

现行的高等数学教材中[1-2]，大部分都是根据通解的结构和自由项形式来求解二阶常系数线性微分方程。文章在此方法的基础上，推导出通解公式，进而代入公式即可求解。

y″+py′+qy=f(x)

(1)

上式为二阶常系数线性微分方程，该方程通解的解法在现行的教材中有个成熟的解法。

1 基础求解方法

方程(1)通解具有此形式：y=Y(x)+y*

其中：Y(x)为方程(1)对应的齐次线性微分方程y″+py′+qy=0(2)的通解 ，y*为方程(1)自身的一个特解

设方程(2)的特征方程λ2+pλ+q=0的两根分别为λ1，λ1≠λ2则：

λ1≠λ2时，Y(x)=c1eλ1x+c2eλ2x

λ1=λ2时，Y(x)=(c1+c2x)eλ1x

λ1,λ2=∂±βi，Y(x)=e∂x(c1cosβx+c2sinβx)

再根据自由项(即f(x)=e∂xQm(x)与f(x)=e∂x(Qm(x)cosβx+Qn(x)sinβx))，求出方程(1)自身的一个特解y*。

例：求方程y″+3y′-y=excos2x的通解。

特征方程为：λ2+3λ-1=0

设方程的一个特解为：y*=ex[Ccos2x+Dsin2x]

则

y*′=ex[(C+2D)cos2x+(D-2C)sin2x]

y*′′=ex[(4D-3C)+(-4C-3D)sin2x]

代入原方程，有(10D-C)cos2x-(D+10C)sin2x=cos2x

比较cos2x与sin2x的系数，得

利用这种方法求解时避免不了的是计算量的繁多，特别是根据f(x)的形式讨论特解的时候。鉴于此，我们可以推导出方程(1)通解的一个公式，只需要求解一个方程。

2 通解公式算法

定理：方程(1)中函数f(x)为连续函数，λ2+pλ+q=0的两个根分别为λ1，λ2，则通解为：

当λ1≠λ2且都为实数根时，可得：

(3)

方程(3)的右边前两项是方程(1)对应的齐次线性微分方程(2)的通解Y(x)，而且当c1=c2=0时，方程(3)即为方程(1)的一个特解[3]。

证明：λ1≠λ2时，方程(2)的通解为Y(x)=c1Y1(x)+c2Y2(x)，

其中：Y1(x)=eλ1x和Y2(x)=eλ2x是方程(2)的两个线性无关的解，所以可设方程(1)的通解为：

y=c1(x)Y1(x)+c2(x)Y2(x)

(4)

c1(x)，c2(x)是关于x的连续函数

对方程(4)求导：得：

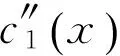
(5)

故

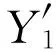
(6)

则

(7)

将方程(4)(6)(7)带入(1)，且Y1(x)，Y2(x)是方程(2)的解，

并化简得：

联合方程(5)(8)得到关于c1(x)与c2(x)的方程组：

由于系数行列式：

解方程组得：

再对上式两边积分，得：

于是[5]，将c1(x)，c2(x)和Y1(x)=eλ1x，Y2(x)=eλ2x代入方程(4)并化简整理可得定理[6-7]。

3 举例

例：求方程y″-5y′+4y=3xex的通解。

解：由λ2-5λ+4=0得：λ1=1,λ2=4

方程的通解为：y=c1ex+c2e4x+y*

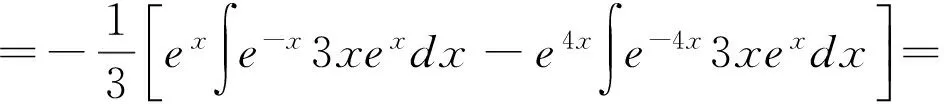
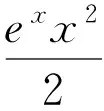
[1]常瑞玲,郑兆顺.高等数学(上册)[M].郑州：河南科学技术出版社，2015.

[2]同济大学数学系.高等数学(下册)第四版[M].上海:高等教育出版社,1998．

[3]孙杰华,杜超雄.一类二阶变系数线性微分方程解的研究[J].邵阳学院学报(自然科学版),2016,13(1):19-22.

[4]张玉兰.二阶变系数线性齐次微分方程的通解[J].长沙大学学报,2013,27(2):1-3.

[5]高杨,王贺元.一类二阶变系数线性微分方程的解法[J].高等数学研究,2014,17(1):81-82.

[6]张道详,李亭亭.一类二阶变系数线性微分方程的新解法[J].科技资讯,2017,20:207-208.

[7]杨秀香.微分方程中常数变易法的应用[J].渭南师范学院学报,2016,31(8):9-13.

SomeSolutionstotheSecondOrderConstantCoefficientLinearNonhomogeneousDifferentialEquation

LI Yingdi

(International School，Huanghe Science and Technology University，Zhengzhou 450000,China)

second order differential equation with constant coefficient; free items; characteristic equation; general solution.

1672-7010(2017)06-0005-04

O175

A

2017-08-22

李迎娣(1985-)，女，回族，河南商丘人，讲师，硕士，从事计算数学研究；E-mail:liyingdi1006@163.com

Received：The author discussed how to solve the second order constant coefficient linear homogeneous differential equation,using the structure of the general solution and the form of the free item,we can solve this equation using the general solution formula.