对称随机变量的若干性质的探究

夏 林，周 可，张海波

(1．安徽信息工程学院 计算机与软件工程系，安徽 芜湖，241000；2．安徽师范大学 经济管理学院，安徽 芜湖，241000；3．安徽师范大学 数学与计算机科学学院，安徽 芜湖，241000)

对称随机变量的若干性质的探究

夏 林1，周 可2，张海波3

(1．安徽信息工程学院 计算机与软件工程系，安徽 芜湖，241000；2．安徽师范大学 经济管理学院，安徽 芜湖，241000；3．安徽师范大学 数学与计算机科学学院，安徽 芜湖，241000)

基于已知的对称随机变量的相关性质和定义进行新的探究，给出了对称随机变量与概率、期望、边际分布函数等有关的若干新性质。

对称随机变量；概率；期望；边际分布函数

随机变量的引进对概率论的研究产生了巨大的影响，我们不再孤立地研究一个问题而是用联系的观点来看待问题。对称随机变量是随机变量中一类重要的变量，对称随机变量相关性质的研究对解决概率论中相关问题具有重要的研究意义。John等人(1972)提出了一种逼近的方法来获得对称随机变量，为对称随机变量性质的研究打下基础[1]；于浩等人(1989)建立了独立随机变量收敛性定理，提出了收敛条件，改进和推广了目前的收敛结果[2]；汪明瑾(1995)提出了对称随机变量的平均不等式，建立了对称随机变量的算术平均，几何平均期望不等式,将康托洛维奇不等式作为推论导出[3]；杨善朝(2000)研究由随机变量和的M_Z_B型不等式导出Rosenthal型不等式的条件,并证明了M_Z_B型不等式,获得了多种类型随机变量序列的Rosenthal型不等式[4]；祝东进(2004)对随机变量的几乎确界进行了研究，讨论在适当的条件下得到随机变量几乎确界的一些性质,并对对称、可逆、倒对称随机变量的几乎确界性质作了进一步的讨论[5]；陈光曙(2005)讨论了对称随机变量、逆对称随机变量、倒对称随机变量的概率结构,并得到了他们之间的关系[6]；赵婷等人(2010) 在一定的矩限制条件下,得到了一个随机变量序列的Hajek-Renyi型不等式,并应用此不等式证明随机变量序列部分和的几乎处处收敛性,同时给出随机变量序列部分和的推广性质和收敛速度[7]；张水利等人(2011)利用Háyek-Rényi型最大值不等式研究了对称随机变量序列，并在一定条件下,得到了对称随机变量序列的强大数定律[8]；朱玉龙等人(2015)讨论了多维对称随机变量,阐明其分量仍是对称随机变量,并进一步给出多维对称随机变量分布函数的一个充分必要条件[9]；朱玉龙等人(2017)阐明了连续型对称随机变量概率密度的偶函数特点[10]；张永波等人(2017)提出检测对称变量的算法，为对称变量的检验提供了有效的途径[11]；然而关于对称随机变量性质的相关研究很少有人关注，这篇文章主要研究了对称随机变量与概率、期望以及边际分布函数等有关的若干性质，为以后对称随机变量的相关问题的研究提供了理论基础。在给出主要的理论结果之前我们先给出相关的准备知识：

定义1：设X是随机变量，如果对于任意的x有P(X≤-x)=P(X>x)，则称随机变量X具有对称分布。

定义2：如果n维随机变量(b1x1,b2x2,…,bnxn)，其中bi=±1，i=1,2,…,n的分布函数均为F(y1,y2,…,yn)=P(x1≤y1,x2≤y2,…,xn≤yn)，则称(x1,x2,…,xn)为n维对称随机变量。

引理2[13]：若随机变量X关于Y是对称的，则与下面的任意一个条件等价：

(1)X-Y与Y-X有相同的特征函数；

(2)X-Y的特征函数是实值函数。

1 主要理论结果

可得P(Xn=0)=1与P(Xn=0)<1矛盾，从而假设不成立，于是结论得证。

证明：构造集合{j:|Tj|≥a,j≤n}，当此集合是空集时，令参数b=n，当此集合不是空集时令b=min{j:|Tj|≥a,j≤n} ，则有

(1)

又由于{xn,n≥1}是对称的随机变量，从而(1)可以化简如下：

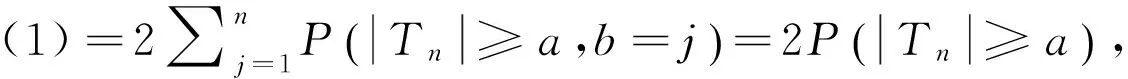
性质4：设(x1,x2,…,xn)是n维对称随机变量

N={1,2,…,n},Ak={a1,a2,…,ak}⊂N,a1≤a2…≤an，

则(TAk,TBn-k)是二维对称随机变量。

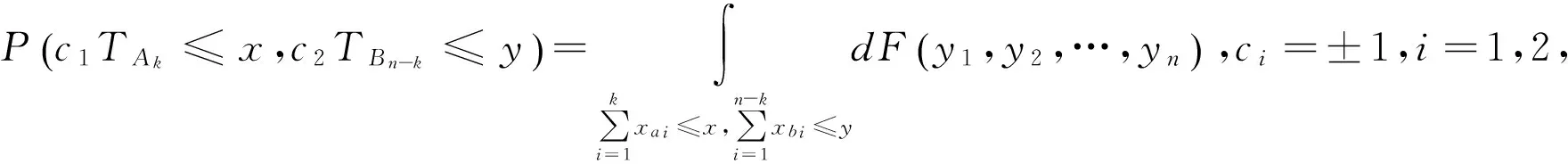
所以(TAk,TBn-k)是二维随机变量。

性质5：设(x1,x2,…,xn)是n维对称随机变量，分布函数为F(y1,y2,…,yn)=P(x1≤y1,x2≤y2,…,xn≤yn)，则(x1,x2,…,xn-2)的边际分布函数为

Fx1,x2,…,xn-2(y1,y2,…,yn-2)=F(y1,y2,…,yn)+F(y1,y2,…,-yn-1-0)+F(y1,y2,…,-yn-0)

证明：因为随机变量(b1x1,b2x2,…,bn-1xn-1)，其中bi=±1，i=1,2,…,n-1，的分布函数为

所以(x1,x2,…,xn-1)是对称随机变量。(x1,x2,…,xn-1)的分布函数，

Fx1,x2,…,xn-1(y1,y2,…,yn-1)=F(y1,y2,…,yn-1,+)=

P(x1≤y1,x2≤y2,…,xn-1≤yn-1,xn≤yn)+P(x1≤y1,x2≤y2,…,xn-1≤yn-1,xn>yn)=

P(x1≤y1,x2≤y2,…,xn-1≤yn-1,xn≤yn)+P(x1≤y1,x2≤y2,…,xn-1≤yn-1,xn<-yn)=

F(y1,y2,…,yn)+F(y1,y2,…,yn-1，-yn-0)

因为(x1,x2,…,xn-1)是对称随机变量，同理可得，(x1,x2,…,xn-2)是对称随机变量，且

从而结论得证。

2 应用举例

例1：设随机变量X关于0是对称的，服从均匀分布U[0,1]，则EX=0。

例2[14]：n维标准正态随机变量X～N(0,I)的分布函数可表示为

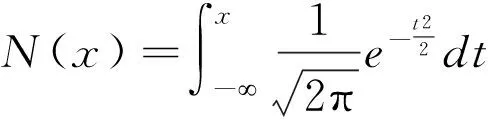
于是(x1,x2,…,xn-2)的边际分布函数为

其中a=(a1,a2,…,an)T=QnT(y1,y2,…,-yn-0)，b=(b1,b2,…,bn-1)T=Qn-1T(y1,y2,…,-yn-1-0)

[1]JOHN S Ramberg; BRUCE W Schmeiser.An approximate method for generating symmetric random variables[J].Communications of the ACM，1974：17(2)：78-82.

[2]于浩．独立随机变量的完全收敛性[J]．应用概率统计，1989，(2):105-116．

[3]汪明瑾.对称随机变量的平均不等式[J].江西师范大学学报(自然科学版),1995,19(4)：301-303.

[4]杨善朝．随机变量部分和的矩不等式[J].中国科学(A辑),2000,30(3):218-222．

[5]祝东进.关于随机变量“几乎确界”的注记[J].安徽师范大学学报(自然科学版),2004,24(4)：307-313.

[6]陈光曙.对称随机变量的概率结构[J].佳木斯大学学报(自然科学版),2005,23(2):236-239.

[7]赵婷,胡舒合,李晓琴,等.一类随机变量的概率不等式及几乎处处收敛性[J].安徽大学学报(自然科学版)，2010，34(1)：7-10.

[8]张水利,屈聪.对称随机变量序列的强大数定律[J].平顶山学院学报,2011,26(2)：13-14.

[9]朱玉龙,谭林.多维对称随机变量分布函数的充要条件[J].数学的实践与认识,2015,45(20)：289-294.

[10]朱玉龙,王婷,谭林.基于对称随机变量构造的反例[J].数学的实践与认识,2017,47(11)：282-285.

[11]张永波,厉晓华.含无关项布尔函数的对称变量检测算法[J].浙江大学学报(理学版)，2017,44(02):186-190.

[12]严士键,概率论基础(第二版)[M].北京：科学出版社，2014.

[13]汪嘉冈,现代概率论基础[M].上海：复旦大学出版社，2005.

[14]周圣武，张艳，韩苗，等.多元正态分布函数的表示[J].大学数学， 2011,27(4)：142-145.

ExplorationofSomePropertiesofSymmetricRandomVariables

XIA Lin1,ZHOU Ke2,ZHANG Haibo3

(1.School of Computer Science and Software Engineering,Anhui Institute of Information Technology,Wuhu 241000,China;2.School of Economics and Management,Anhui Normal University,Wuhu 241000,China;3.School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241000,China)

symmetrical random variables; probability; expectations; marginal distribution function.

1672-7010(2017)06-0015-04

O212.1

A

2017-08-24

安徽师范大学科研创新与实践项目(2016yks044，2016yks046)

夏林(1992-)，男，安徽巢湖人，硕士，从事高维统计推断研究；E-mail：1491357861@qq.com

Received：Based on the known properties and the definition of symmetrical random variables to make a new exploration,we found some new properties involving probability,expectation and marginal distribution function on symmetrical random variable.