非线性单摆周期的数值解

陈大伟，斯小琴

(安徽建筑大学 城市建设学院，安徽 合肥，238076)

非线性单摆周期的数值解

陈大伟，斯小琴

(安徽建筑大学 城市建设学院，安徽 合肥，238076)

应用计算机软件和微分方程数值解的Euler法，研究了非线性单摆运动过程中角度与时间的微分关系，模拟出大角度单摆周期的高精度近似解，并作出时间随摆角的变化曲线。将所得模拟值与实验值比较可知,该方法避免了解繁琐的微分方程，可简捷、快速得到周期较高精度的数值解，在解决相关实际问题中有一定的价值。

单摆周期；Euler法；数值解

单摆是一种理想物理模型，是指一端固定且不可伸长的细线与可视为质点的物体相连，质点在竖直平面内绕固定端作小于5°的摆动[1]。而当摆角大于5°则不可再近似为线性单摆，其运动问题也变得较为复杂，这类复杂问题成为大学物理教学中关注的热点问题[2-6]。对非线性单摆的讨论，无论是获得近似解的格林函数法[7]、渐进法[8]，还是获得精确解的解析法[9]，都避免不了繁琐的数学计算。利用常微分方程数值解的Euler法格式，并借助计算机可简捷、快速地得到非线性单摆的高精度近似解[10-13]，这给解决此类实际问题提供了一种有效而便捷的方法。

1 理论基础

一端固定且不可伸长的细线与可视为质点的物体相连，当它在竖直平面内以一定角度摆动，在摆动到中间任意角度θ位置时，其动力学方程为：

(1)

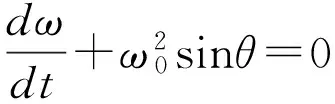
(2)

将(2)式进行变换，有

(3)

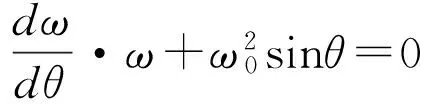
(4)

将(4)式分离变量后两边积分，得

(5)

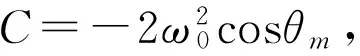
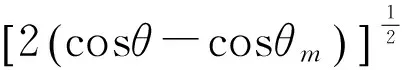
(6)

正负号取决于计时起点。为方便讨论这里取正，这样有

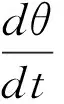
(7)

为能利用角的始末条件，将(7)变换为

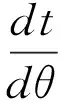
(8)

对于初始条件为t(θ0=θm)=0的(8)式常微分方程，其数值解的Euler法格式为：

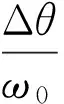
(9)

2 数值模拟及结果分析

g取9.8m/s2，摆长l取2.45m以使问题具体化。θm取若干大角度(≥5°)，基于Euler法格式利用微软EXCEL的下拉填充公式可快速模拟出N个角值点对应的时间数值解，其中

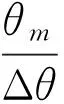
角度步长Δθ取0.1°，即可得到精度较高的数值解。

由于θ=±θm不可代入Euler法格式，且单个点对整体误差较小、对函数曲线走向无影响，故数值模拟时除起始点θ0=θm，令t=0外，其他θ=±θm点略去，θ=±θm的时间以相邻角值点时间作修正获得。现仅取θ0=±0°、±θm四个特征角处时间列入表1中。

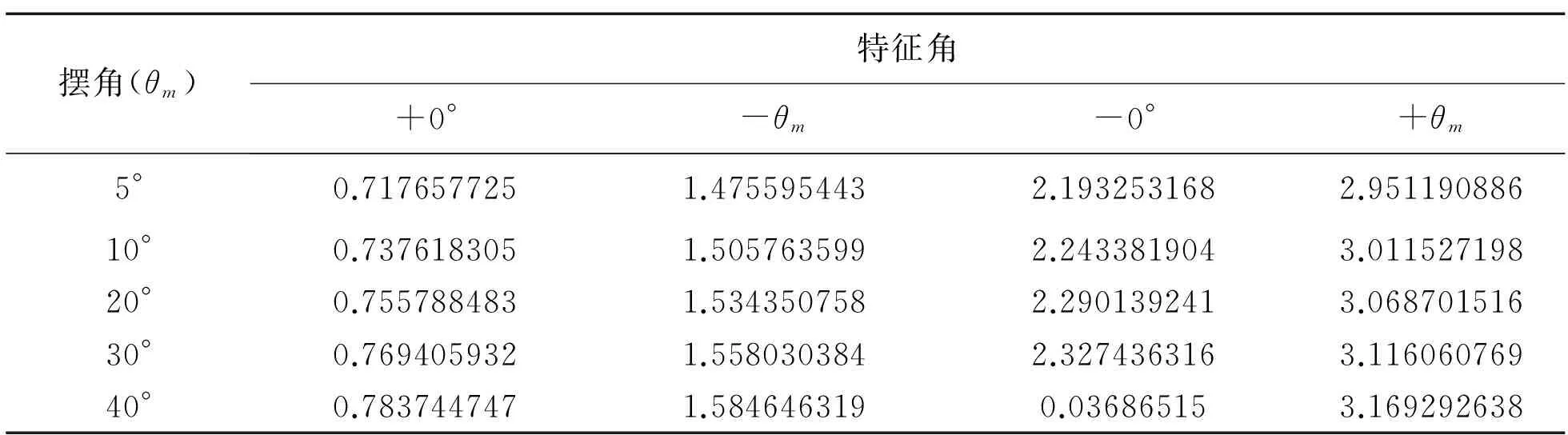
表1 特征角所对应时间列表Table 1 The time list of characteristic angle

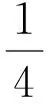
图1 时间随角度变化曲线Fig.1 The series curve of angle

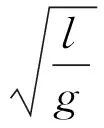
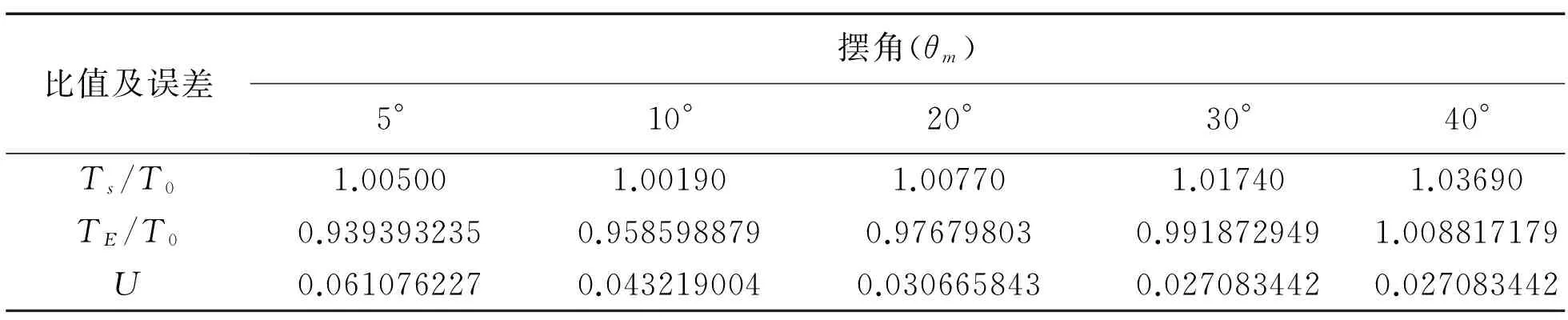
表2 Ts/T0与TE/T0对比及误差表Table 2 The list of Ts/T0 with TE/T0 and error table

从表2中可发现随着摆角增大，Ts与T0之间比值也增大，这样在大摆角下还用T0作周期就不再适合。而TE与Ts间的相对误差随着摆角增大而减小，这就意味着大摆角下周期更适合用TE作为周期。

3 讨论

(1)实验不可能达到完全无阻尼的条件，所以周期的实验值应比真值要大，这是实验值与模拟值之间产生误差的一个因素；

(2)文中对往返-θm模拟时进行了忽略，并将返回θm-Δθ角的时间加上3倍θm至θm-Δθ的时长作为周期，此种处理会使由-θm返回θm时间变短，这是产生误差的另外一种因素；

(3)数值解本质就是一种近似求解方法，产生误差不可避免。所取角度步距Δθ越小误差会越小，计算角值点也会越多，但是基于计算机软件会很好地解决该困难；

(4)在精度要求范围内，取合适角度步距Δθ并借助计算机软件，会便捷快速得到大摆角单摆周期的数值解，这给解决此类实际问题提供了一种有效而便捷的方法。

[1]赵近芳,王登龙.大学物理学[M].北京：北京邮电大学出版社,2014.

[2]魏慧军,朱炯明.大角度单摆的周期[J].上海师范大学学报(自然科学版),2004,33(3):103-105.

[3]龚善初.利用线化和校正法求非线性单摆运动的周期[J].大学物理,2006,25(2):16-18.

[4]PINOT Patrick,GENEVES Gerard.Numerical simulation for designing tuned liquid dampers to damp out double-pendulumoscillations[J].Measurement Science & Technology,2011,22(6):065103.

[5]邓永菊,王世芳,吴涛.非线性单摆运动的计算机仿真[J].湖北第二师范学院学报,2010,27(2):59-61.

[6]KAZMIERCZAK Marek,KUDRA Grzegorz,AWREJCEWICZ Jan,et al.Mathematicalmodeling,numerical simulations and experimental verification of bifurcation dynamics of a pendulum driven by a dc motor[J].European Journal of Physics,2015,36(5): 13.

[7]孙春峰.非线性单摆的格林函数解法[J].大学物理,2004,23(1):9-11.

[8]黄卫立,龚善初.非线性单摆的微扰解[J].江西师范大学学报(自然科学版),2000,24(2):9-11.

[9]潘军廷,范梦慧,龚伦训.非线性单摆的Jacobi椭圆函数解[J].大学物理,2006,25(11):23-26.

[10]杨明波,卢建立,杨敏.利用Excel的循环引用自动完成迭代计算[J].计算机应用与软件,2008,25(12):103-105.

[11]柳宏德.基于Mathematica求解任意摆角下的单摆周期近似公式[J].大学物理,2014,33(11):52-53.

[12]陶利.大角度单摆运动问题的计算机模拟[J].中国西部科技,2010,9(8):42-43.

[13]孙进,丁宗玲.关于单摆运动的数值模拟与分析[J].赤峰学院学报(自然科学版),2016,32(24): 4-6.

TheNumericalSolutionoftheNonlinearPendulumPeriod

CHEN Dawei，SI Xiaoqin

(Urban Construction College,Anhui Jianzhu University,Hefei 238076,China)

single pendulum cycle; Euler method; numerical solution

1672-7010(2017)06-0001-04

O411.1

A

2017-11-05

安徽高校自然科学研究项目(KJ2017A810)；安徽高校自然科学研究项目(KJ2015ZD16)

陈大伟(1985-)，男，安徽巢湖人，讲师,硕士,主要从事大学物理教学研究工作

Received：By application of computer software and differential equation numerical solution of Euler method,The differential relation between angle and time in nonlinear pendulum motion was studied,the high precision approximate solution of single pendulum cycle was simulated and the change curve of time with the angle of swing was given.The comparison of simulation value with experiment value showed that this method could avoid the complicated differential equation and it is simple and quick to obtain the numerical solution with high precision,so it has some value in solving relevant practical problems.