一类非线性机电换能器混沌系统的最优控制

苏 敏，雷腾飞，黄丽丽，付海燕，曹 凤

(齐鲁理工学院 电气信息工程学院，山东 济南，250200 )

一类非线性机电换能器混沌系统的最优控制

苏 敏，雷腾飞，黄丽丽，付海燕，曹 凤

(齐鲁理工学院 电气信息工程学院，山东 济南，250200 )

针对一类自激非线性机电换能器混沌系统，首先，采用分岔图、Lyapunov指数谱图与复杂度分析了系统的混沌基本动力学行为；其次，基于的最优控制理论，找出了系统的HJB微分方程，可随意跟踪目标函数；最后，通过MATLAB软件对最优控制器进行了相关的仿真，仿真结果表明设计的最优控制器比传统的控制器具有更强的快速响应能力且在工程中易实现。

机电换能器；混沌；Lyapunov指数; 最优控制

半个多世纪以前， Lorenz 首先提出了第一个混沌模型——Lornez系统，自此，较多的科学工作者对混沌以及相关领域开始给予了关注并进行了初步研究探索[1-2]。在非线性电路、力学、化学与生物等领域，人们都发现了复杂的混沌特性，尤其是在机电耦合系统更为突出，因多数系统通过Vanderpol振子与Duffing振子耦合而成的。近年来，在机电耦合与电机方面驱动成果丰硕，文献[3]对永磁同步电机混沌系统的相关动力学进行了分析并采用电路实现了系统相图；文献[4，5]对分别对永磁同步风力发电机与永磁同步电机系统采用反步控制策略进行了控制；文献[6]对一类具有分数阶永磁同步风力发电机进行了自适应控制的研究，最后采用电路将其实现；文献[7]对一类同步磁阻电机混沌系统采用自适应滑模控制将其成功实现控制。文献[8]讨论了具有串补电容的单机无穷大电力系统的余维3动态分叉。文献[9，10]考虑了具有自动频率跟踪功能的电磁振动给料机的机电耦合系统的余维2动态分叉。文献[11]给出了振动筛系统的两类余维3分岔与非常规混沌演化等。随着人们对机电耦合混沌系统的建模、分析、控制与同步的深入研究，大量的复杂非线性现象及系统的内在混沌动力学行为被揭示，同时基于不同策略的混沌控制与同步方法在实验和应用中得到广泛验证。文献[12]推导了一种平面内三连杆的自由浮动刚柔耦合冗余度空间机械臂的动力学模型，并给出了鲁棒Proportional-Derivtive(PD)补偿控制、延迟反馈控制和模态力最优控制策略。文献[13,14]对此类机电耦合Vanderpol-Duffing系统，分别采用自适应反步控制及无源化控制策略，将其系统稳定控制。

文中针对一类非线性换能系统的动力学数学模型，利用分岔图、Lyapunov指谱以及分岔空间等基本的动力学分析方法，研究了参数对系统的影响，对系统进行了定性的阐述；同时根据最优控制原理，设计出了非线性换能系统的控制器，；最后采用MATLAB软件对设计的有限时间控制策略以及k值进行了仿真，仿真结果表明了控制器的快速性和可控性，对机电以及电机耦合系统的同步控制研究均提供了重要的价值。

1 混沌系统

非线性自激励机电换能器如图1所示，从图中可以看出系统由电力和机械两部分构成.其中电类部分由电容(C)、电感(L)和非线性电阻(RNL)组成。

图1 自激励机电换能器Fig.1 Nonlinear electromechanical transducer

经过实践尺度变换,换能器系统动力学模型为[13]：

(1)

其中x,y分别表示电容电荷和质量为m的杆的位移.若p=q=0,则系统(1)即为经典的Vanderpol振子和自治的Duffing方程,所以该系统具有自激励性能。

为了研究方便，重新改写机电换能器混沌系统(1)为

(2)

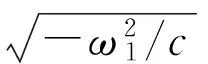
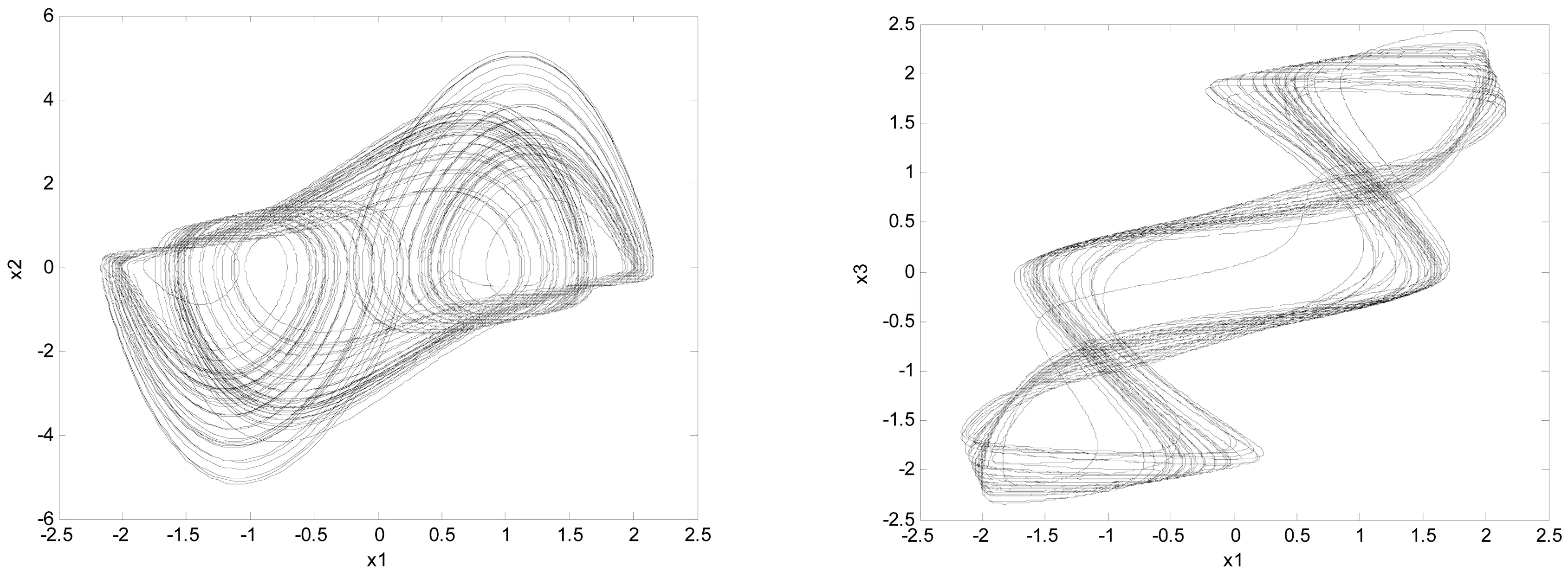
(a)x1-x2相图 (b)x1-x3相图

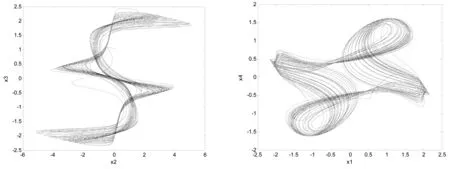
(c)x2-x3相图 (d)x1-x4相图图2 系统(2)混沌吸引子Fig.2 Chaotic attractor of system(2)

2 参数换能系统的影响

对于非线性换能系统，文中通过常用的分岔图、Lyapunov指数谱(LE谱)以及复杂度SE/C0对参数ω1对系统的影响予以分析。

改变参数ω1，其他参数不变，参数ω1∈[0,2]，系统随ω1变化的分岔图与LE谱图如图3所示，最大Lyapunov指数如图3(c) 所示，从图中易观察出，ω1∈[0,0.72)系统处于周期状态如图3(a)系统分岔图，对应此区间最大Lyapunov指数小于0。如图3(c)，ω1∈[0.72,0.82)∪[1,1.2]∪[1.7,2]系统处于混沌态，此区间最大Lyapunov指数大于0。由此可见分岔图与LE谱图具有一致,同时，也可以看出该系统混沌区域较小，为了进一步验证系统的混沌态与周期态，文中给出了系统不同参数值下的相图，如图4所示。

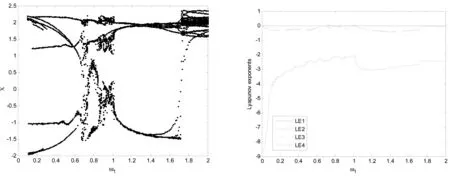
(a)分岔图 (b)LE谱

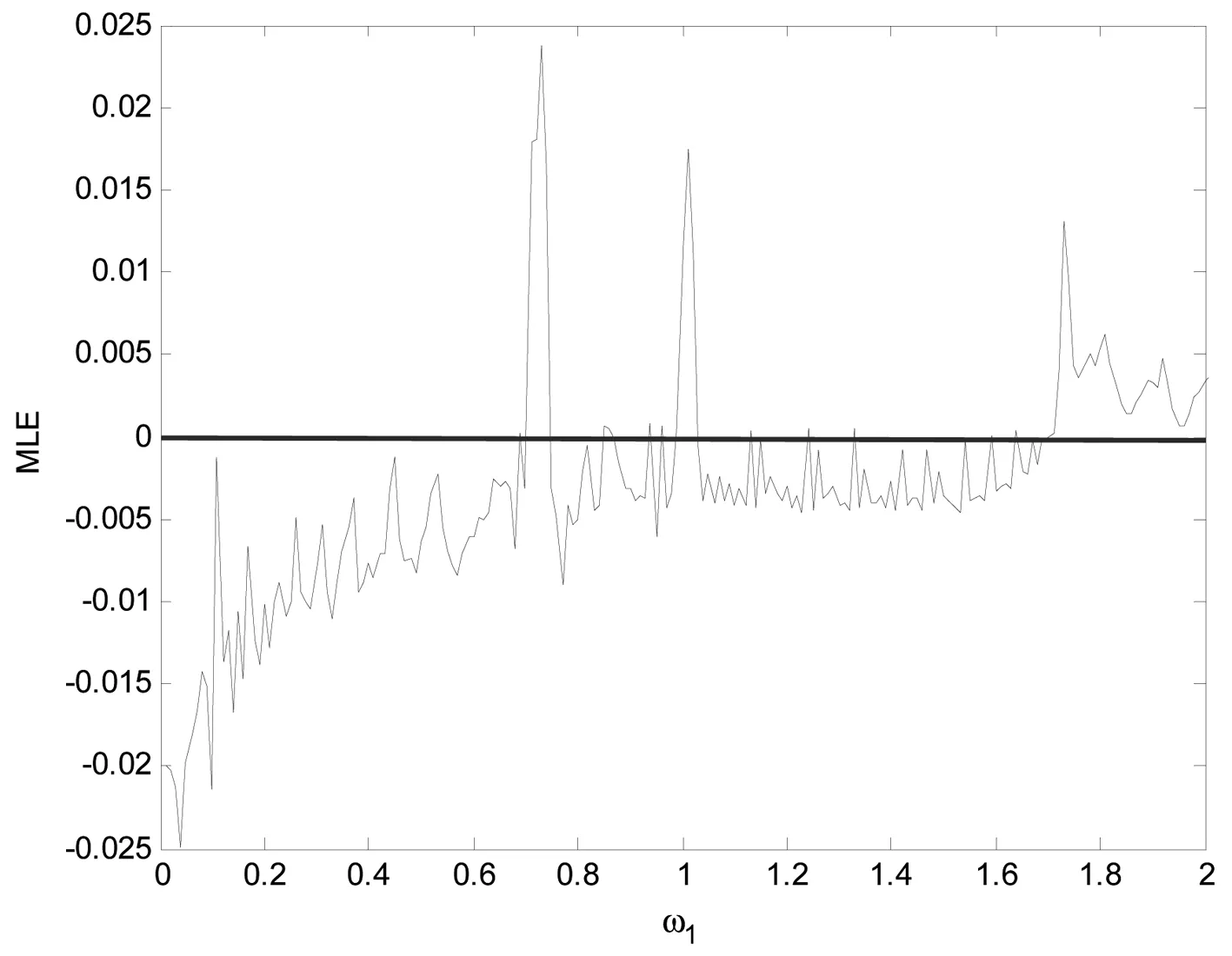
(c)最大Lyapunov指数图3 系统随a变化的分岔图与LE谱Fig.3 Bifurcation diagram for the system with a varying and Lyapunov exponent spectrum

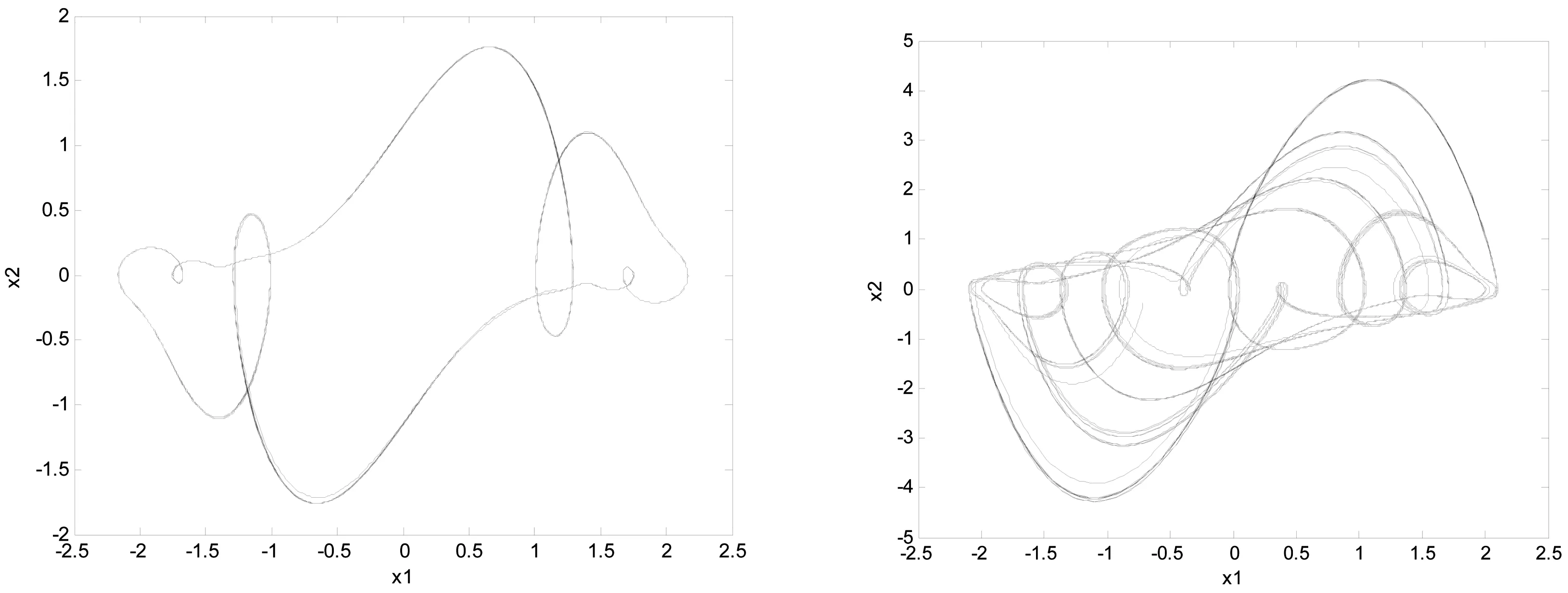
(a)ω1=0.6 (b)ω1=0.7

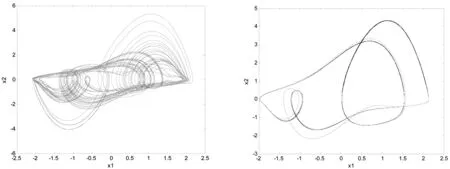
(c)ω1=0.72 (d)ω1=0.82

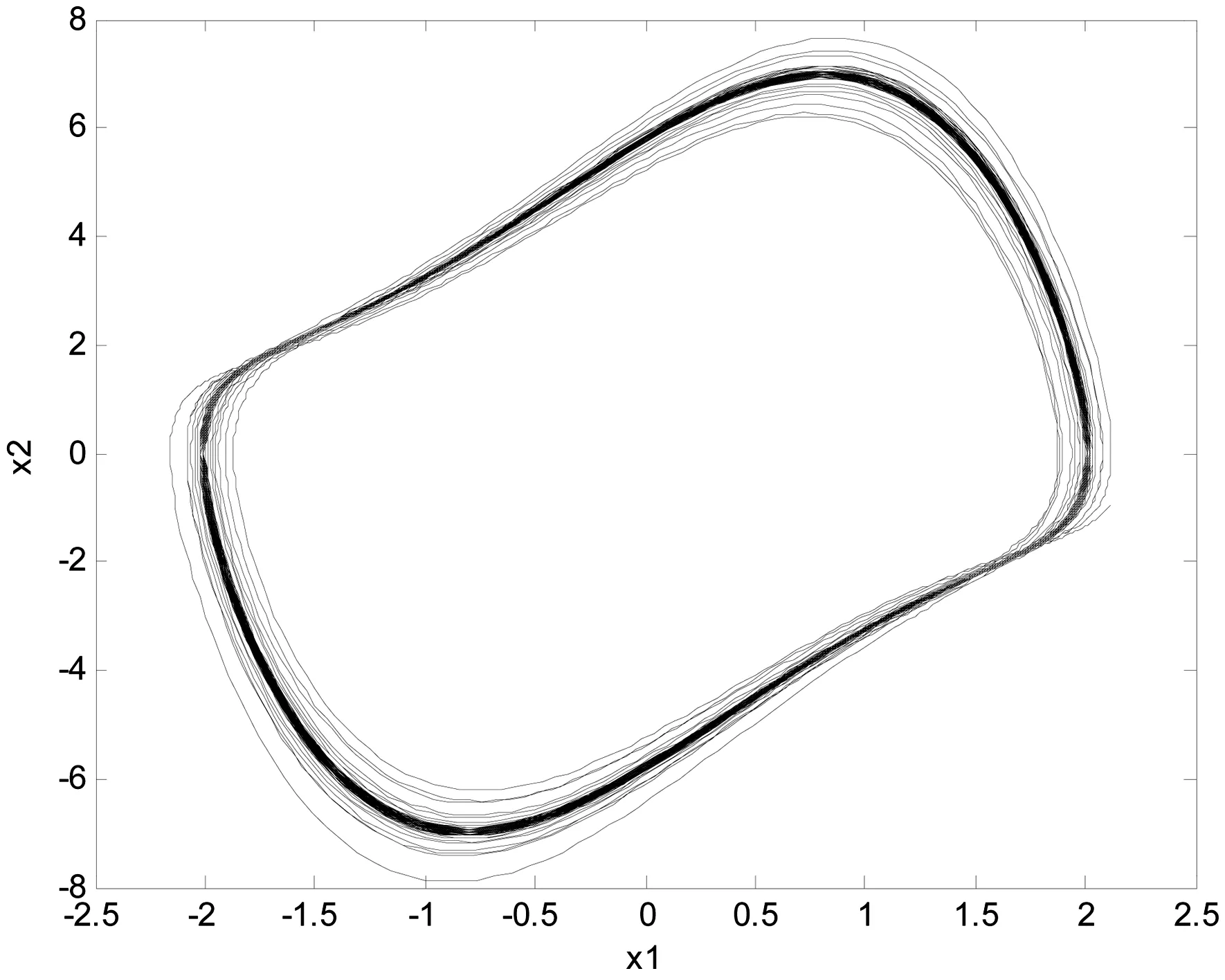
(e)ω1=2图4 ω1变化时系统(2)的相图Fig.4 Phase diagram for system(2)with ω1 varying

3 最优控制器设计原理

对于非线性系统而言：

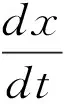
(3)

x=(x1,x2…xn)T为状态变量，u(x,t)为控制器[11]，驱动系统从任意点到任意确定点x*的目标函数为：

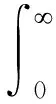
(4)

q(x)是连续可导且是正定的函数。根据动态规划原理，最优控制则归结为HJB微分方程[12];

(5)

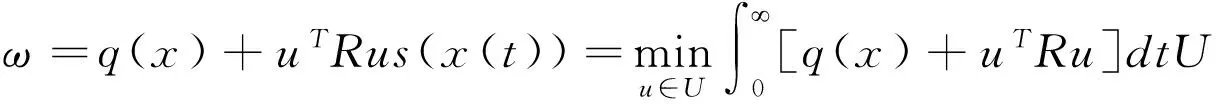
4 系统的最优控制器设计

(6)

取前馈系统为：

(7)

则系统(6)变成:

(8)

为了达到控制点，确定反馈控制器u(u1,u2,u3,u4)，定义目标函数：

(9)

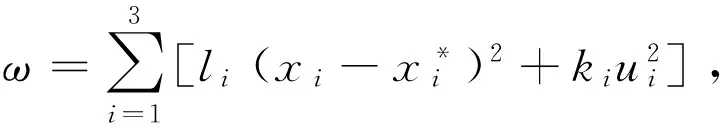
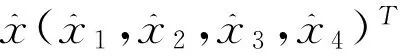
(10)

+

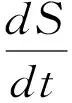
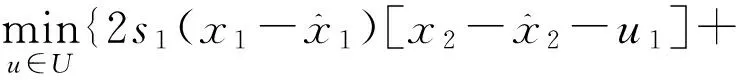
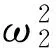
(11)

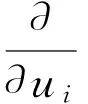
(12)

其中si,ri(1,2,3,4)为正整数。

将(12)代入(11)得：

5 系统控制器的仿真与分析

为了研究上面所述控制策略的有效性，为了便于进行仿真实验，取与文献[14]相同参数值，令ε2=0.00987，ε1=2.466，ω1=ω2=1，c=0，p=3.518，q=0.808，取k1=k2=1,k3=5,，s1=1,s2=s4=1,s3=5，l1=3,l2=1.02,l3=11,l4=6.932,当系统运行到10s，加入最优控制器，系统可以迅速跟跟踪到制定目标，仿真结果如图5所示，从图中可以看系统响应以及抗干扰性较强。

(a)状态变量x1的受控时序图 (b)状态变量x2的受控时序图

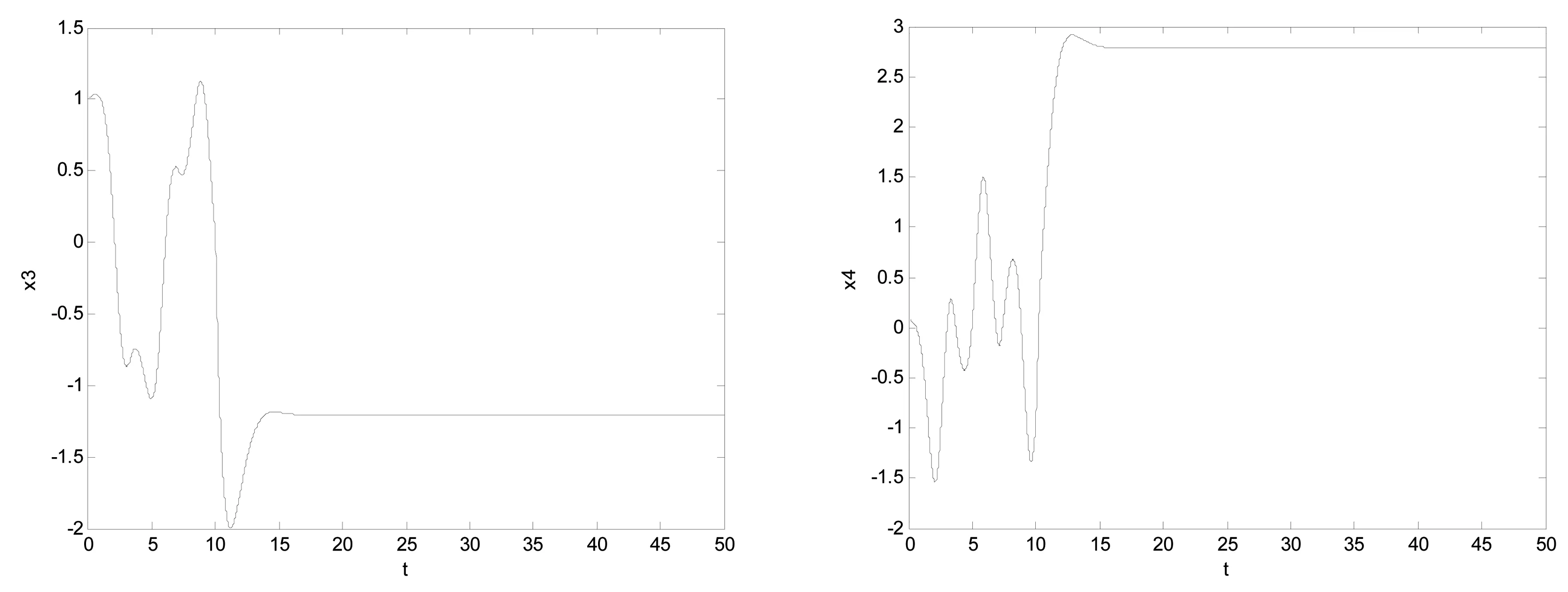
(c)状态变量x4的受控时序图 (d)状态变量x4的受控时序图图5 受控系统的状态Fig.5 State of the controlled system

6 结论

文中针对一类自激非线性机电换能器混沌系统，运用基本动力学分析工具分叉图与Lyaunov指数谱等进行了系统动力学的分析，并给出系统出现混沌现象的区域。同时利用最优控制理论即寻找HJB微分方程，文中给出了具体寻找的步骤，最后采用Matlab软件，验证了文中控制器的的可行性与有效性。从仿真结果看，系统具有良好的时间响应。

[1]LU J G.Nonlinear observer design to synchronize fractional- order chaotic system via a scalar transmitted signal[J].Physica A,2006,359:107-118.

[2]雷腾飞,刘彦芬,陈众起,等．一类具有吸引子共存新混沌系统的动力学分析、电路仿真及应用[J].曲阜师范大学学报(自然科学版),2017,43(3):35-43．

[3]薛薇，郭彦岭，陈增强.永磁同步电机的混沌分析及其电路实现[J].物理学报，2009,58(12):8146-8151.

[4]郑刚,邹见效,徐红兵，等.直驱型永磁同步风力发电机组中混沌运动的反步自适应控制[J].物理学报,2011,6(60):1-8.

[5]杨晓辉,刘小平,柳和生，等.基于永磁同步电机反推方法混沌运动的同步控制[J].电测与仪表,2012,49(12):37-40.

[6]雷腾飞，陈恒，王震，等.分数阶永磁同步风力发电机中混沌运动的自适应同步控制[J].曲阜师范大学学报(自然科学版)，2014，40(3)：63-68

[7]雷腾飞，康杰，刘彦芬，等.同步磁阻电机系统的混沌特性与反馈控制[J].邵阳学院学报(自然科学版)，2017，14(3):34-39.

[8]邱勇,邱宇,邱家俊.机电耦联系统余维3动态分岔研究[J].力学学报，2006，38(3)：421-428.

[9]韩清凯，秦朝烨，闻邦椿.自同步振动系统的稳定性与分岔[J].振动与冲击，2007，26(1)：31-34.

[10]张琪昌，田瑞兰.一类机电耦合非线性动力系统的余维2动态分岔[J].工程力学，2009，26(1)：216-220.

[11]张永祥，孔贵芹，俞建宁.振动筛系统的两类余维3分岔与非常规混沌演化[J].物理学报，2008，57(10)：6182-6187.

[12]王从庆，吴鹏飞，周鑫.基于最小关节力矩优化的自由浮动空间刚柔耦合机械臂混沌动力学建模与控制.物理学报,2012,61(23):230503.

[13]WANG Zhen,WU Yuntian,LI Yongxin,et al.Adaptive Backstepping Control of a Nonlinear Electromechanical System with Unknown Parameters[C]//Proceedings of the 4 th International Conference on Computer Science and Education,2009,441-444.

[14]王震.非线性机电换能器混沌系统的无源化控制[J].控制理论与应用，2011，28(7)：1036-1040.

OptimumControlforANonlinearElectromechanicalTransducerChaoticSystem

SU Min,LEI Tengfei,HUANG Lili,FU Haiyan，CAO Feng

(Sclool of Electrical and Information Engineering，Qilu Institute of Technology,Jinan 250200,China)

electromechanical transducer；chaos ；Lyapunov exponent.； optimum control

1672-7010(2017)06-0054-08

TP273;TM346;TN702；TM132

A

2017-09-30

山东省自然科学基金(ZR2017PA008)；齐鲁理工学院科技计划项目(07qlk009)

苏敏(1983-)，女，辽宁沈阳人，副教授，硕士，主要从事传感器检测与混沌检测技术研究；雷腾飞(1988-)，男，山东肥城人，硕士，讲师，主要从事混沌系统分析与控制等研究

Received：In this paper,a class of self-excited nonlinear electromechanical transducer chaotic system was proposed.Firstly,the chaotic basic dynamics behavior of the system was analyzed by using bifurcation diagram,Lyapunov exponent spectrum and complexity.Secondly,based on the optimal control theory,the HJB differential equation of the system was found,and the target function could be tracked at random.Finally,the optimal controller was simulated by MATLAB software,the simulation results show that the optimal controller has more rapid response ability than the traditional controller and is easy to implement in the project.