超欠挖状态下支护结构的力学特性研究
2017-12-22李树忱孙爱花张露晨
李树忱,朱 林,孙爱花,张露晨,谢 璨,晏 勤
(山东大学 岩土与结构工程研究中心,山东 济南 250061)
超欠挖状态下支护结构的力学特性研究
李树忱,朱 林,孙爱花,张露晨,谢 璨,晏 勤
(山东大学 岩土与结构工程研究中心,山东 济南 250061)
在传统的喷射混凝土支护结构设计中,通常假设支护结构层是一个薄壁等厚层。钻爆法开挖的隧道围岩表面由于受爆破的影响存在不同程度的超欠挖,导致初期支护喷射混凝土结构层厚度不均匀。充分考虑超欠挖情况下隧道围岩表面的不平整性,根据喷射混凝土支护厚度将支护后的隧道表面不规则形状依据实际喷层情况归结为未完全填充、局部填充和完全填充三类。基于弹性力学厚壁圆筒理论,建立了单一喷射混凝土支护结构和喷射混凝土+钢格栅联合支护结构的等效刚度与最大支护力的理论公式。基于上述原理,结合收敛-约束法对某隧道开挖工程的稳定性进行了分析,得到了隧道支护结构的安全系数。结果表明,所提出的方法对超欠挖隧道的稳定性分析具有较好的适用性,验证了该方法的可行性。
不规则围岩表面;厚壁圆筒理论;等效支护刚度;等效最大支护力;收敛-约束法
随着社会经济水平的持续发展,国家对各项基础设施建设力度的不断加大,城市地铁、公路隧道、铁路隧道等越来越多,隧道等地下空间的建设呈现出明显的增长趋势[1]。当前在建和拟建的隧道中有相当部分采用钻爆法开挖,而钻爆法开挖的隧道中普遍存在超欠挖现象[2]。因此,研究隧道的超欠挖对支护结构稳定性的影响具有重要的意义。
传统的喷射混凝土衬砌的设计方法一般采用工程类比法或假定喷射混凝土层是一个薄壁等厚结构,尤其是在采用钻爆法开挖的隧道中。例如,李树忱等[3]提出适用于膨胀性黄土隧道的“格栅拱架+钢拱架+喷射混凝土”联合支护方式,利用弹性薄壳理论建立了联合支护的力学分析模型,研究表明所建立的模型和方法对膨胀围岩条件下初期支护的力学特性分析具有较好适用性。陈五二[4]以金沙洲隧道为背景,采用基于有限单元法的荷载结构模型,对按围岩类别设计的3种隧道断面衬砌结构受力进行数值模拟,通过对计算结果分析验证,选出各围岩级别下合适的衬砌结构。康红普[5]根据地质和采矿特点,将复杂条件下的煤矿巷道划分为5种类型,对每种类型巷道围岩的变形破坏特征进行了分析,详细介绍了各种巷道支护技术,并分析了4种典型的支护加固实例,指出锚杆支护已成为主流的巷道支护形式。
实际工程中钻爆法开挖的隧道普遍存在超欠挖现象,但在以往研究中的假定与实际情况存在出入。因此本文充分考虑超欠挖情况下隧道开挖断面的不规则性和喷射混凝土层的覆盖厚度,将断面形状分类。基于弹性力学厚壁圆筒理论,分别推导了单一喷射混凝土支护结构和喷射混凝土+钢格栅联合支护结构的等效刚度与最大支护力的计算公式,结合收敛-约束法研究了隧道超欠挖对支护结构稳定性的影响。
1 基本概念
1.1 基本超欠挖形状
鉴于钻爆法隧道普遍存在超欠挖,本文对超欠挖形成的不规则形状作了统一的简化,将由于超欠挖而形成的不规则形状现场统一简化如图1所示。图1(d)所示的形状的基本特征由d,L,α等多项参数确定,这些形状特征参数均可通过现场量测得到。将图1(d)中的形状看成是直角梯形(包括虚线部分),延长直角边和虚线相交,设延长的直角边线段长为h,则根据三角形相似定理有:

图1 隧道现场与简化对比Fig.1 Tunnel site and simplified diagram
式中,Li,L1i,L2i,di,d1i,d2i等参数所表示的距离均可由图1(d)得出,由式(1)和式(2)可以得到:
1.2 喷射混凝土断面
当围岩的等级和性质不同时,由于超欠挖造成的不平整形状和规模也不一样。一般V级围岩超欠挖最小,II级围岩超欠挖最大;即一般软岩超欠挖小,而硬岩超欠挖大[6-7]。同时不同等级的围岩所需要的喷射混凝土厚度不一样,喷射混凝土与围岩的交界面面积也不一样,形成的喷射混凝土断面形状也就必然存在差异。本文依据现场实际将喷射混凝土断面简化并归类为3种基本类型,如图2所示。
图2(a)为第1类断面,表示在粗糙的岩石表面覆盖一层较薄的喷射混凝土层,覆盖后的喷射混凝土断面与原围岩断面的轮廓变化不大即未完全填充。图2(b)为第2类断面,表示在岩石表面覆盖一层薄喷射混凝土层之余,还对超欠挖形状的底部进行了适当的填充即局部填充。图2(c)为第3类断面,表示喷射混凝土将超欠挖形成的凹凸不平完全填充,在此基础上再覆盖喷射混凝土形成一个较光滑的表面轮廓即完全填充。

图2 3种简化后的表面轮廓和简化力学模型Fig.2 Three simplified surface profiles and simplified mechanical models
为了便于分析,将图2中不规则表面采用ts,dr,d等多项参数来表示其表面特征。隧道表面的各项特征参数一般有两种方式获得:第1种方式为先判别该段断面属于第几类断面,再将所有超欠挖形成的不平整形状用简化的锯齿形状表征,而简化的锯齿形状的特征参数可以现场测量出来,再将每个简化的模型断面用特征参数表示,将所得到的各个参数分别求平均值即可得到该段断面的特征参数;第2种方式为各类断面分别取多个有代表性的不平整形状,先得到它们的特征参数,再分别取平均值。上述2种方式的特征参数均可通过现场量测得到,通过上述2种方式,其表面特征参数的平均值为
式中,下标j为第j类断面的综合;下标i为第i个简化断面形状;n为选取的断面数量;tjs为第j类断面平均喷射混凝土厚度;dr为楔形体底部平均厚度;α为平均不规则角度。
第3类断面的喷射混凝土层厚度tsi为
2 等效力学特性
围岩表面与喷射混凝土的相互作用影响着两者交界面的各项性质,如边界条件、受力状况等,而围岩和喷射混凝土之间的相互作用又受到隧道超欠挖的尺寸、形状和喷射混凝土厚度的影响。
2.1 围岩/喷射混凝土层等效力学特性
为了简化计算,本文以连续岩体中的圆形隧道为例,假设隧道某一段水平方向上围岩的超欠挖趋于一致,即该段隧道的超欠挖形状和喷射混凝土厚度在隧道开挖轴线方向上无变化。同时依照前文定义,得到简化的超欠挖形状和平均喷射混凝土厚度,用平均喷射混凝土厚度替代假设的喷射混凝土厚度。
考虑半径为R的隧道内设厚度为tc的喷射混凝土衬砌,基于厚壁圆筒的弹性应变理论,径向位移可表示为
式中,ur为半径r处的径向位移;A,B为积分常数。
根据轴对称的几何关系,筒壁内每个点只有径向位移和纵向位移,且均与环向角度无关。由于隧道长度一般远大于隧道直径,满足平面应变条件。故纵向位移为零,因此平面内只有一个位移分量。几何方程可写作:
故径向应变和切向应变为
根据Hook定律,σr,σθ可表示为
式中,Ec为喷射混凝土弹性模量;νc为喷射混凝土的泊松比。
将式(9)和(10)代入式(11)和(12),得到:
支护边界条件为
联立式(8),(12)~(15)可得积分常数A,B分别为
将式(16),(17)代入式(13)得:
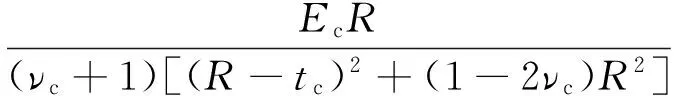
由边界条件σr|r=R=ps及ps=ksus可得喷射混凝土支护刚度为
依据弹性力学厚壁圆筒理论,将围岩与喷射混凝土替换成一个等效的围岩/喷射混凝土层,如图3所示。图3(a)表示圆形隧道的等效围岩/喷射混凝土层及弹塑性边界,图3(b)表示一微元体上的应力状态,图3(c)表示超欠挖状态下等效的围岩/喷射混凝土层厚度的内外半径,其中te表示等效喷层厚度,一般从超挖最严重的底部开始计算。
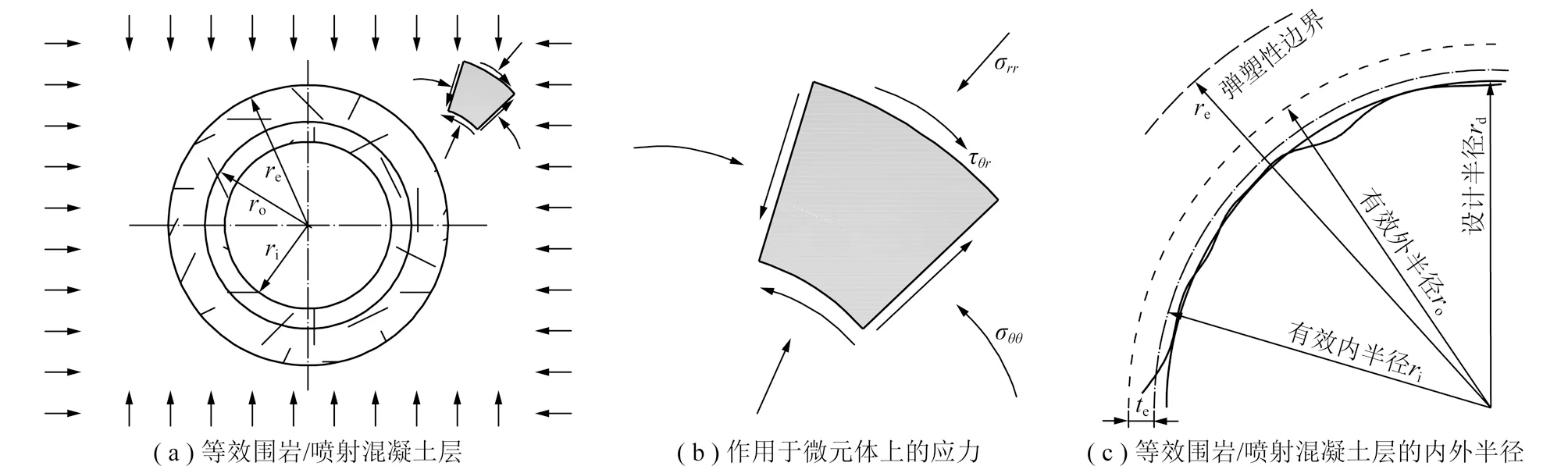
图3 围岩局部示意Fig.3 Schematic diagram of partial surrounding rock
考虑围岩表面的不规则性和喷射混凝土的覆盖厚度,将围岩和喷射混凝土替换为一个等效厚壁圆筒,等效层的厚度、弹性模量、泊松比等参数也随之发生变化,并且不同的喷射混凝土覆盖厚度其对应的各项参数也必然不同。结合前文定义对应三类喷射混凝土覆盖厚度的等效厚壁圆筒厚度te为
考虑等效厚壁圆筒环向应力的平衡[8],得到有关等效弹性模量和等效泊松比的平衡方程:
式中,EEQ为等效弹性模量;Er为岩石的弹性模量;Ec为喷射混凝土的弹性模量;νEQ为等效泊松比;νr为岩石的泊松比;νc为喷射混凝土的泊松比;x,y分别为等效环中岩石与喷射混凝土所占比例,故有x+y=1。
结合前文对围岩表面不规则形状的简化和对喷射混凝土覆盖断面的简化,可以得到:
式中,d为平均超欠挖深度;L为平均超欠挖长度;dr为填充超欠挖底部的平均喷射混凝土厚度;ts为平均喷射混凝土厚度。
借鉴式(19),并将泊松比和弹性模量等参数采用等效参数替代,得到等效刚度:

式中,te为等效厚壁圆筒的厚度;ri为等效厚壁圆筒的内半径。
依据弹性力学的厚壁圆筒理论,当支护达到最大支护压力时,支护内边界最先出现破坏,此时可得到最大支护力:
式中,σc为喷射混凝土的单轴抗压强度。
当考虑围岩与喷射混凝土交界面之间的相互作用时,最先出现破坏的不一定是支护内边界。首先,破坏可能出现在临近喷射混凝土的岩体中,此时:
式中,σEQ为围岩/喷射混凝土层的抗压强度;σr为岩体的抗压强度。
其次,破坏可能出现在喷射混凝土中,此时:
最后,围岩与喷射混凝土的交界面上可能会发生剪切破坏。当破坏发生时,交界面上受到的环向应力为0,即σrr=0,对围岩与喷射混凝土的交界面进行受力分析,如图4所示。取交界面上的一段微元Rdα,为了便于计算,对微元的方向进行调整,使σθ处于竖直方向,如图5所示。
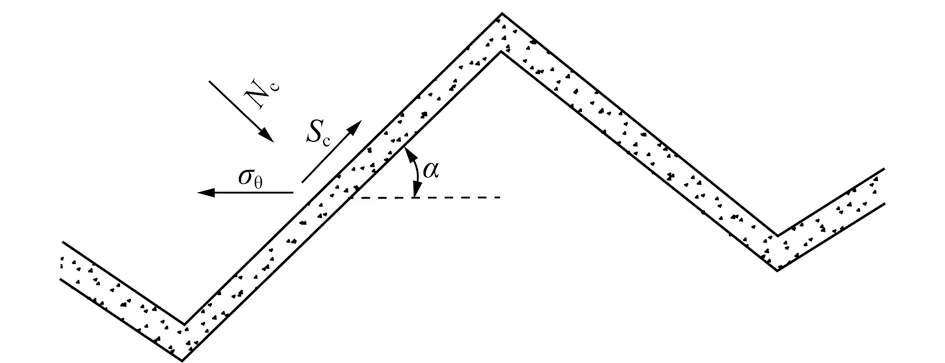
图4 围岩/喷射混凝土交界面受力分析Fig.4 Stress analysis on the interface of rock/shotcrete

图5 交界面上微元结构受力分析Fig.5 Stress analysis of the element on the interface
假设微元在σθ方向上受力为Fθ,则有:
对微元进行受力分析知,微元的切向分力和法向分力分别为
故交界面上的切向应力和法向应力为
当围岩与喷射混凝土的交界面发生剪切破坏时有:
式中,τsi为交界面的抗剪强度,结合公式(35)和(37)可以得到:
可见当0°≤α≤45°时,α越大,交界面上所能承受的环向应力σθ越小,破坏越容易出现;τsi越大,交界面上所能承受的环向应力σθ越大,支护结构的最大支护力越大。
综合上述3种情况,当支护结构出现破坏时,围岩/喷射混凝土等效层的抗压强度应为三者中的最小值,即:
所以,当考虑围岩表面的不规则性和喷射混凝土的覆盖断面时,支护结构的最大支护力为
2.2 联合支护结构的等效力学特性
钢格栅与喷射混凝土能够较容易的结合在一起,它们可以组成整体结构,形成钢筋混凝土结构体系,在受到围岩荷载压力的作用时不容易产生收缩裂缝。而与之相反,型钢拱架与喷射混凝土很难黏结在一起形成整体结构,并且型钢拱架周围容易产生裂缝[9]。因此本文主要研究钢格栅+喷射混凝土的联合支护。
图6所示为格栅拱架与喷射混凝土结构单元,S1和S2分别表示钢格栅和喷射混凝土,SEQ为等效后的支护结构,其中,b为组合结构单位长度;s为格栅拱架之间的间距;n=b/s;t为格栅拱架与喷射混凝土初期支护结构厚度;tEQ为等效后的支护结构的厚度。

图6 格栅拱架与喷射混凝土结构单元Fig.6 Element of lattice girder reinforced shotcrete
鉴于钢格栅与喷射混凝土结合良好,假设格栅拱架与喷射混凝土之间不存在相对位移[10]。基于此项假设,将格栅拱架与上文所述的围岩/喷射混凝土环视作均质壳体结构,对其一微元结构受力分析,如图7所示,根据文献[11]可得:
式中,M,N为组合结构的弯矩和轴力;M1,M2为钢格栅与围岩/喷射混凝土层的弯矩;N1,N2为钢格栅与围岩/喷射混凝土层的轴力;K1,K2分别为钢格栅与围岩/喷射混凝土层的抗弯系数,K=EI/(1-ν2);D1,D2分别为钢格栅与围岩/喷射混凝土层的抗压系数D=EA/(1-ν2)。

图7 微元结构上的力Fig.7 Loads acting on the differential length Rdθ
组合结构的弯矩、轴力与各组成部分所承担的弯矩、轴力之间的关系为
结合图6知等效部分的抗弯系数KEQ1和抗压系数DEQ1为
联立式(45)~(48),可得等效厚度和等效弹性模量:
借鉴式(24)得等效泊松比:
式中,ν1,ν2分别为钢格栅与围岩/喷射混凝土层的泊松比;x,y分别为钢格栅与围岩/喷射混凝土层在联合支护结构中所占比例。
结合式(28)知,联合支护结构的支护刚度:

按照并联结构整体稳定判定原则,组合支护结构允许变形由各个支护单元中允许变形中最小的支护单元决定。设组合结构变形量为
式中,u1,u2分别为钢格栅与围岩/喷射混凝土层的允许极限变形。则组合结构的最大支护压力:
3 工程实例
某隧道位于闽浙交界,左洞全长约2 400 m,右洞全长约2 408 m,隧道走向为60°,隧道设计半径为6 m。隧道围岩主要为风化溶结凝灰岩和风化凝灰质砂岩,属于较坚硬岩。隧洞洞身穿越Ⅱ,Ⅲ,Ⅳ,Ⅴ级围岩,地质条件变化起伏较大。
[12-13],根据收敛-约束理论得到隧道围岩特征曲线方程如下:

支护结构特征曲线方程[14]为
式中,P为支护结构的约束反力;u为支护结构的位移;u0为初始位移;um为围岩自由变形的最大位移;l为开挖后施作的支护结构距掘进工作面的距离。
3.1 喷射混凝土支护实例
左洞桩号ZK48+516~ZK48+625段围岩支护采用锚喷支护,喷射混凝土层厚15 cm,依据现场实际情况简化后的断面形式属于第三类断面。根据现场量测数据,采用式(1)~(7)得到该段平均超欠挖深度d=0.138 m,ts=0.035 m,等效围岩/喷射混凝土层厚度te=0.173 m。喷射混凝土弹性模量Ec=23 GPa,泊松比νc=0.25,单轴抗压强度σc=12.5 MPa;围岩的各项参数见表1。
表1隧道围岩参数
Table1Mechanicsparametersofsurroundingrock

P0/MPaEr/MPac/MPaφ/(°)νr2.3768.51.2300.24
根据以上围岩参数并参考式(55)得到围岩特征曲线,如图8所示,得到um=4.39 mm。隧道开挖后及时施作锚喷支护,减小风化和围岩质量恶化,故假定式(58)中l≈0,求得u0=1.351 mm。根据式(22)~(24),(27)~(29),求得围岩/喷射混凝土等效层的弹性模量EEQ=12.93 GPa,泊松比νEQ=0.245,等效刚度kEQ=55.679 MPa。参考文献[15]并结合现场实际情况判定支护内边界最先达到抗压强度极限值,所以最大支护力Pmax=0.345 MPa。相应的支护特征曲线如图8所示。
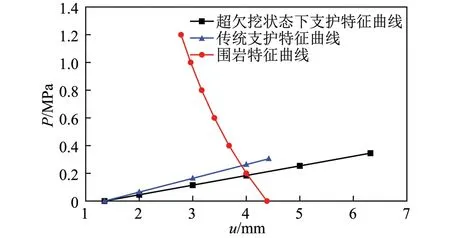
图8 锚喷支护的围岩-支护特征曲线Fig.8 Ground-supporting characteristic curve for shotcrete
由图8得达到平衡时的支护压力Pb=0.189 MPa,根据曲线判断喷射混凝土未达到极限支护力,稳定性系数fs=Pmax/Pb=1.825,初期支护处于稳定状态。
不考虑超欠挖状态时,由式(19)可得喷射混凝土支护刚度ks=99.3 MPa/m,最大支护力Psmax=0.302 MPa,进而由式(57)得到支护特征曲线公式,如图8所示,可得其支护压力Psb=0.224 MPa,稳定性系数fs=Pmax/Psb=1.348。
由图8可知,传统支护特征曲线平衡时支护力比考虑超欠挖状态下大,这与采用工程类比法设计支护结构时,为保证围岩稳定,喷射混凝土的厚度一般存在冗余的实际相符。但超欠挖状态下支护特征曲线最大支护力更大,稳定性系数更好。
3.2 联合支护实例
右洞桩号YK49+204~YK49+298段围岩支护选用锚喷加钢格栅联合支护,钢格栅的间距为每榀1.0 m,断面尺寸为16 cm×16 cm的正方形断面,格栅主筋采用φ22 mm的钢筋,格栅的其他相关系数见表2。喷射混凝土层厚20 cm,简化后的断面形式属于第三类断面,基于现场量测数据,采用式(1)~(7)得到该段平均超欠挖深度d=0.124 m,ts=0.087 m,等效厚度te=0.211 m。围岩各项参数见表3。
表2钢格栅支护参数
Table2Supportingparametersoflatticegirder

E1/GPaν1A1/m2I1/m42000.251.52×10-37.285×10-6
表3隧道围岩参数
Table3Mechanicsparametersofsurroundingrock

P0/MPaEr/MPac/MPaφ/(°)νr2.9084.20.5300.25
类似上例:根据围岩参数并参考式(55)得到围岩特征曲线,如图9所示,得到um=7.342 mm,类似上例有u0=2.259 mm。围岩/喷射混凝土等效层的弹性模EEQ2=13.791 Pa,泊松比νEQ2=0.25,等效刚度kEQ2=82.777 MPa/m,最大支护力Pm2=0.417 MPa。
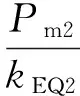

K1=1.554 MN·m2,D1=324.37 MN
K2=11.408 MN·m2,D2=3.081 GN
钢格栅单独发挥作用时:

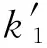
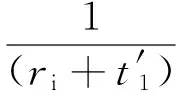

联合支护共同发挥作用时:


νEQ1=xν1+yν2=0.25,kEQ=96.836 MPa/m
ulim=min{u1,u2}=5.043 mm,
pmax=kEQulim=0.488 MPa
根据上述计算结果,得到超欠挖状态下支护特征曲线,如图9所示。
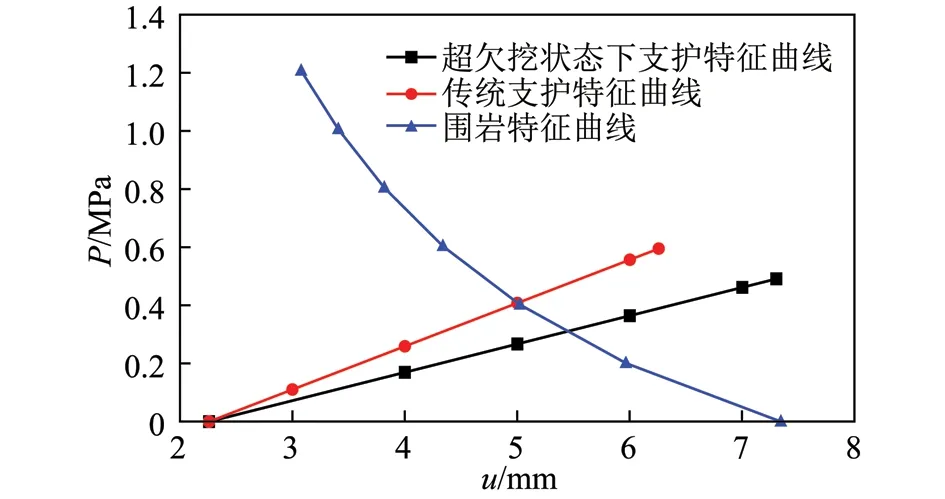
图9 联合支护的围岩-支护特征曲线Fig.9 Ground-supporting characteristic curve for combined supporting
由图9可得达到平衡时Pb=0.304 MPa,根据曲线判断喷射混凝土未达到极限支护力,稳定性系数fs=1.606,说明初期支护处于稳定状态。
不考虑超欠挖状态时,喷射混凝土支护刚度ks=99.3 MPa/m,最大支护力Pm2=0.397 MPa,u2=3.998 mm,K1,D1,u1保持不变。
K2=16.177 MN·m2,D2=4.869 GN


kEQ=147.993 MPa/m
ulim=min{u1,u2}=3.998 mm
pmax=kEQulim=0.592 MPa
根据上述计算结果,得到相应的传统支护特征曲线,如图9所示,得Psb=0.401 MPa,稳定性系数fs=1.476。对比知,传统支护特征曲线的最大值力及平衡时的支护力均比考虑超欠挖状态下的最大支护力和平衡支护力大,但超欠挖状态下的支护特征曲线的稳定性系数更好。
4 结 论
(1)根据弹性力学厚壁圆筒理论,得到了围岩/喷射混凝土层的等效刚度和最大支护力。同时基于钢格栅与喷射混凝土之间不存在相对位移的假设,得到了联合支护下的等效刚度和最大支护力。
(2)考虑围岩表面不规则性的情况下,在单一喷射混凝土支护时,最先破坏部位不一定是衬砌内表面,也可能是围岩表面或围岩与喷射混凝土交界面出现破坏。当破坏出现在围岩与喷射混凝土的交界面时,围岩/喷射混凝土等效层的最大支护压力与交界面的抗剪强度和岩体表面不规则角度α有关。抗剪强度越小,最大支护压力越小;当0°≤α≤45°时,α越大,最大支护压力越小。
(3)基于收敛-约束原理,采用本文提出方法对某隧道案例进行了分析,得到了单一喷射混凝土支护和喷射混凝土+钢格栅联合支护作用下的隧道安全系数,验证了该方法的可行性。
(4)传统支护特征曲线平衡时的支护力比考虑超欠挖状态下的平衡支护力大,这与工程类比法下为保证围岩稳定,喷射混凝土的厚度一般存在冗余的实际相符。在采用考虑隧道超欠挖的分析方法下,可以得到更好的稳定性系数。
参考文献(References):
[1] 《中国公路学报》编辑部.中国隧道工程学术研究综述·2015[J].中国公路学报,2015,28(5):1-65.
Editorial Department of China Journal of Highway and Transport.Review on China’s tunnel engineering research:2015[J].China Journal of Highway and Transport,2015,28(5):1-65.
[2] 魏继红,孙少锐,彭建忠,等.高速公路连拱隧道超挖预测及评价研究[J].岩石力学与工程学报,2006,25(S1):3324-3329.
WEI Jihong,SUN Shaorui,PENG Jianzhong,et al.Sdudy on forecasting and evaluation of overbreak in double-arch tunnels of highway[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(S1):3324-3329.
[3] 李树忱,晏勤,谢璨,等.膨胀性黄土隧道钢拱架-格栅联合支护力学特性研究[J].岩石力学与工程学报,2017,36(2):446-456.
LI Shuchen,YAN Qin,XIE Can,et al.The study on mechanical behavior of composite supports of steel-grid in loess tunnel[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(2):446-456.
[4] 陈五二.基于有限单元法的隧道抗水压衬砌结构设计[J].铁道工程学报,2007,24(7):67-70.
CHEN Wuer.Structure design of tunnel water-pressure resisting lining based on FEM[J].Journal of Railway Engineering Society,2007,24(7):67-70.
[5] KANG Hongpu.Support technologies for deep and complex roadways in underground coal mines:A review[J].International Journal of Coal Science & Technology,2014,1(3):261-277.
[6] 王明年,关宝树.隧道超欠挖的统计规律及其对隧道可靠度的影响[J].岩土工程学报,1997(1):83-88.
[7] 肖云华,陈剑平,张鹏,等.隧道超欠挖断面轮廓分形特征[J].吉林大学学报(地),2010,40(1):153-158.
XIAO Yunhua,CHEN Jianping,ZHANG Peng,et al.Fractal feature of overbreak-underbreak figure of tunnel section[J].Journal of Jilin University(Earth Science Edition),2010,40(1):153-158.
[8] WINDSOR C R.Structural design of shotcrete linings[A].Proceedings of Australian shotcrete conference[C].IBC conferences,Sydney,1998:1-34.
[9] 冯丙阳.膨胀性黄土隧道大变形演化特征及支护对策研究[D].济南:山东大学,2014.
FENG Bingyang.The study on large deformation evolution characteristics and supporting technology of swelling loess tunnels[D].Jinan:Shandong University,2014.
[10] 李树忱,冯丙阳,马腾飞,等.隧道格栅拱架喷射混凝土支护力学特性[J].煤炭学报,2014,39(S1):57-63.
LI Shuchen,FENG Bingyang,MA Tengfei,et al.Researches on mechanics behavior of lattice girder reinforced shotcrete support for tunnels[J].Journal of China Coal Society,2014,39(S1):57-63.
[11] CARRANZA-TORRES C,DIEDERICHS M.Mechanical analysis of circular liners with particular reference to composite supports.For example,liners consisting of shotcrete and steel sets[J].Tunnelling and Underground Space Technology,2009,24(5):506-532.
[12] 苏永华,刘少峰,王凯旋,等.基于收敛-约束原理的地下结构稳定性分析[J].岩土工程学报,2014,36(11):2002-2009.
SU Yonghua,LIU Shaofeng,WANG Kaixuan,et al.Stability analysis of underground structures based conconvergence-confinement method[J].Chinese Journal of Geotechnical Engineering,2014,36(11):2002-2009.
[13] CARRANZA-TORRES C,FAIRHURST C.The elasto-plastic response of underground excavations in rock masses that satisfy the Hoek-Brown failure criterion[J].International Journal of Rock Mechanics and Mining Sciences,1999,36(6):777-809.
[14] HOEK E,BROWN E T.Practical estimates of rock mass strength[J].International Journal of Rock Mechanics and Mining Sciences,1997,34(8):1165-1186.
[15] 唐雄俊.隧道收敛约束法的理论研究与应用[D].武汉:华中科技大学,2009.
TANG Xiongjun.Study on the convergence-confinement method and its application in tunnel construction[D].Wuhan:Huazhong University of Science & Technology,2009.
Mechanicalanalysisofsupportstructurebasedonover-under-excavatedtunnels
LI Shuchen,ZHU Lin,SUN Aihua,ZHANG Luchen,XIE Can,YAN Qin
(GeotechnicalandStructuralEngineeringResearchCenter,ShandongUniversity,Jinan250061,China)
Conventionally,the traditional design of shotcrete support structure has assumed that support structure is a prismatic layer with uniform thickness.Due to the influence of blasting,the surrounding rock surface of the tunnel with drilling and blasting method has different degrees of over-under-excavation,which results in the uneven thickness of the initial support structure layer.In the consideration of the possibility of rock surface irregularities caused by over-under-excavation,this paper,according to the shotcrete thickness,divides the irregular surface of the tunnel after supporting into three categories:not fully filled,partially filled,and fully filled.With utilizing the thick-wall cylinder theory of elastic mechanics,the theoretical formula of the parameters,such as equivalent support stiffness and maximum support pressure,are established under the support of shotcrete or shotcrete+steel grid.Based on the research findings mentioned above,this work analyzes the stability of a tunnel excavation project with the aid of the convergence-confinement method and calculates the safety factor of the support structure.The results show that the proposed method has a preferable applicability to the stability study of over-under-excavated tunnel,and the availability is verified preliminarily.
irregular surface of the surrounding rock;thick-wall cylinder theory;equivalent support stiffness;equivalent maximum support pressure;convergence-confinement method
李树忱,朱林,孙爱花,等.超欠挖状态下支护结构的力学特性研究[J].煤炭学报,2017,42(11):2817-2825.
10.13225/j.cnki.jccs.2017.0638
LI Shuchen,ZHU Lin,SUN Aihua,et al.Mechanical analysis of support structure based on over-under-excavated tunnels[J].Journal of China Coal Society,2017,42(11):2817-2825.doi:10.13225/j.cnki.jccs.2017.0638
TD353
A
0253-9993(2017)11-2817-09
2017-05-09
2017-07-21责任编辑常 琛
国家自然科学基金面上资助项目(51379113);国家重点研发计划资助项目(2016YFC0600803)
李树忱(1973—),男,黑龙江齐齐哈尔人,教授,博士生导师,博士。Tel:0531-88399180,E-mail:shuchenli@sdu.edu.cn
