“算两次”原理在高中数学竞赛中的应用
2017-12-22江西省南城一中344700
江西省南城一中 (344700)
韩海保
“算两次”原理在高中数学竞赛中的应用
江西省南城一中 (344700)
韩海保
“算两次”,也称做富比尼(G.Fubini)原理,是一种非常重要的数学方法.所谓算两次,是指用不同的方法或者从不同的角度对同一个量进行计算,当两次都得到精确值时,我们就得到一个等式,当为估计式时,我们就得到一个不等式,从而使问题得以解决.这种方法的精神实质与“换个角度看问题”是一致的.在算两次中,常考虑的计算对象有:数、点、元素、对子、子集等等.本文通过举例说明算两次原理在恒等式,集合与元素,计数论证,几何,函数等方面的应用,愿能起到举一反三的作用,以利于提高学生的竞技能力.
一、证明恒等式
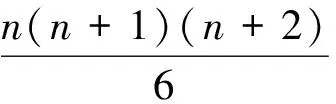
证明:考虑在n+2个数1,2,…,n+2中任取3个的取法总数S.

综上可知结论成立.

二、集合与元素
例2 (2017年东南数学奥林匹克高一试题)设集合S={(a,b)|a∈{1,2,…,m},b∈{1,2,…,n}},A为S的子集.若不存在正整数x1,x2,x3,y1,y2,y3,使得x1 解:将每一个点对(a,b)对应到平面直角坐标系上坐标为(a,b)的点,其中a∈{1,2,…,m},b∈{1,2,…,n}. 一方面,设A取到S中x=1,y=1,y=n的所有点,易知此时|A|=2m+n-2. 另一方面,设A中一系列不少于3个点的列为第i1,i2,…,ik列,对于每一列,除了纵坐标最大和最小的点,剩下的点用它对应的纵坐标来标记它,则对每一个纵坐标,至多被标记1次,则共至多标记n-2次,即该k列中至多有2k+n-2个点,其余m-k中至多2(m-k)个点,故点的个数小于或等于2k+n-2+2(m-k)=2m+n-2. 综上可知,集合A的元素个数的最大值为2m+n-2. 一方面,将A中n个元素作全排列,其不同排列总数为n!个. 另一方面,将子集Ai的|Ai|个元素排在前|Ai|个位置,子集Ai的余集中的元素排在后n- |Ai|个位置,即成排列(x1,x2,…,x|Ai|,y1,y2,…,yn-|Ai|),这样的排列共有|Ai|!(n-|Ai|)!个,它们全包含在全排列数n!中. 以下只要说明,以m个子集A1,A2,…,Am中的元素排在前面,以它们的对应余集中的元素排在后面的各个排列之间,在题设条件之下,没有两个是相同的. 不妨设|Ai|≤|Aj|.由条件知,Ai⊄Aj,故排列(x1,x2,…,x|Aj|,y1,y2,…,yn-|Aj|)中的前|Ai|个元素,绝不会与排列(x1,x2,…,x|Ai|,y1,y2,…,yn-|Ai|)中的前|Ai|个元素完全相同,否则就有Ai⊆Aj,而与条件矛盾. (2)由(1)及柯西不等式即知 评注:许多关于集合的问题可以从两个方面去考虑:一个集合含有哪些元素,一个元素属于哪些集合,然后将这两个方面综合起来,导出结论. 例4 6个点,每两个点之间有一条线相连,线染上红色或蓝色.证明一定有两个以这些点为顶点的三角形,每个三角形的边是同一种颜色(可能有公共的边). 解:我们称三边同色的三角形为同色三角形.设有x个这样的三角形,则三边不全同色的三角形的个数是C36-x. 考虑这个图中同色角(即由两条同色的边组成的角)的个数S. 一方面,每个同色三角形中有3个同色角,每个边不全同色的三角形中有一个同色角,所以S=3x+(C36-x)=2x+20(1). 另一方面,如果一个顶点引出r条红色的边,那么以这个顶点为顶点的同色角的个数C2r+C25-r≥C23+C22=4,所以S≥6×4=24(2). 综合(1)、(2)得x≥2,故问题得证. 评注:数学家厄尔多斯(Erdos)应用这种“从总和经平均到单独”的方法解决了许多问题,其中要点是对总和计数,我们依照厄尔多斯的说法,称之为计数论证.本例可以看成由平均数(≥4)来估计总数. 图1 解:如图1,作BC的中线AD,G当然在AD上,考虑面积,设ΔABC的面积为1,ΔAB1C1的面积为S,我们用两种方法来计算S. 评注:很多几何问题都可通过两方面找到中间量的关系得出结果. 例6 设函数f:N→N(即定义域为N,函数值也在N中),满足(ⅰ)f严格增;(ⅱ)对所有m,n∈N,f(mn)=f(m)f(n);(ⅲ)f(2)=4.求f(2017). 解:由(ⅱ),f(n)=f(1)f(n),所以f(1)=1. 设对于小于等于n的数x∈N,均有f(x)=x2. 若n+1为合数,设n+1=ab,1 若n+1为质数,则n+2为合数,从而与上面相同,f(n+2)=(n+2)2.一方面f2(n+1)=f((n+1)2)>f(n(n+2))=n2(n+2)2,从而f(n+1)≥(n+1)2; 另一方面,取整数k>(n+1)4.设h∈N满足nh-1<(n+1)k 世界上有许多复杂的事件,只有从多个侧面去观察,才能把握它的实质.解数学题也是如此.如从一个方面不能解决,就必须改从其他方面考虑,绝不坚持一条道走到黑,这就是算两次的精神所在.




三、计数论证
四、几何问题





五、函数问题
