对一道教材阅读题的深思

江苏省徐州市铜山区启星中学 (221116)

王兴月

对一道教材阅读题的深思

江苏省徐州市铜山区启星中学 (221116)

王兴月

苏教版教材《必修5》第102页第10题，题目是：

案例1 (阅读题)甲、乙两同学分别解“x∈[1,+∞)，求函数y=2x2+1的最小值”的过程如下：

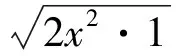
乙：因为y=2x2+1在[1,+∞)上单调递增，所以y的最小值是2×12+1=3.

试判断谁错？错在何处？[ 1 ]

由于这道题是在习题中的“探究 ．拓展 ” 部分，且题前标注的是“阅读题” ，因此，有些老师和学生对它并没有重视起来，或者只是就题论题没有真正的去探究拓展.其实，它是“不等式”这一章中不可多得的一道好题.

此时我看火候已到，便从上节课的作业中抽取几种典型的错误解法投影在屏幕上让学生分析，题目是(苏教版教材第106页“探究 ．拓展 ”第16题)：

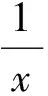
丙：因为x,y均为正数，且1=x+ 2y≥

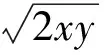
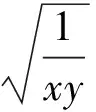
有了案例1的铺垫，学生明白丙犯了类似甲的第二处错误，原因是：

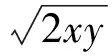
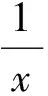
课堂上让学生的“百花齐放，百家争鸣”，取代教师的“一言堂” ，充分暴露他们的思维，把讲台交给学生、把舞台留给学生、把时间还给学生、把空间让给学生.哪怕学生的想法是错误的，也应给予鼓励和赏识.“不愤不启，不悱不发”教师适时地给予点拨和引导，让学生在积极参与、主动探究的基础上收获知识和愉悦.

对于本题的正确解法，学生大多用的是最常见的“1的代换 ”略解如下：

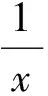
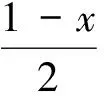
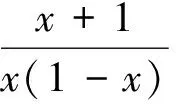
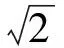
例题的讲解应注重思路的分析，少讲：“如何解，如何写” ，多讲：如何想，为何这样想”.总结解题的过程与思路，让学生动口、动手、动脑，决不能就题论题，要针对学生的典型错误选编纠错补救练习或变式引申.

教学过程中出现了“碰壁”千万不要回避，要让学生认真分析“碰壁”的原因.其实，学习的过程就是一个反复尝试错误的过程，即美国心理学家桑代克提出的：“试误理论”.数学中的每一个概念、定义、定理都有它各自的产生背景、适应范围、限制条件.要培养学生自主探索的理性思维和数学实践的操作能力，避免因思维不严或对问题的片面理解而掉入思维定势的陷阱.

教师在讲解例题时应一题多解，一题多变、多题一解.一题多解并非简单的方法的罗列，“横看成岭侧成峰，远近高低各不同.”应从多角度、多方位、多层次的进行观察分析，总结解题规律，找出知识的内在联系.这样才能形成牢固的知识网，做题时才能左右逢源得心应手，应在通性通法的基础上寻求一题多解探索巧解，若忽视了通性通法一味地追求巧解，学生一旦遇到较为繁杂的题目将会产生厌烦的情绪，打消他们的学习兴趣.

“我们再回到案例1上来，那么，由乙的解法你想到了什么？”我问.

学生答：“在求函数的值域或最值时，若用基本不等式行不通，可考虑用函数的单调性来求解.”.接着我做了总结“一正、二定、三相等，不等利用单调性”.

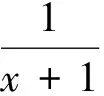
有的学生看过题目配凑后用基本不等式来求解，其解法如下：

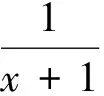
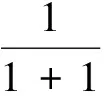
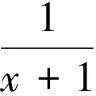
由此可以看出江苏高中数学教材的编写理念是阶梯式前进，螺旋式上升.如果说案例1是抛砖，那么案例2即为引玉.案例3就是雕玉成器.案例1涵盖了运用基本不等式求函数最值时容易出错的内容.且给出了求函数值域或最值的另一种方法——函数的单调性法.案例1在基本不等式这一部分中起到了上穿下连的作用，可以说教材中的这三个探究拓展题(案例1、案例2、案例3)是一脉相承、交相互映、浑然一体的，这也正是教材编写者的匠心所在.教师不仅要能熟练地解答教材中的每一个例题习题，更重要是能够洞察出题目所蕴含的数学思想方法及知识间的相互联系，且能改编一些具有针对性的习题.有些内容教材惜墨如金、言犹未尽，教师要能敏锐地捕捉到其相关信息，凡是学生能看出的教材不必多言，留给学生更多的想象空间；凡是教师能领会到的教材也无需啰嗦，让教师去探究拓展.体现出教材的凝练性、内涵性、外延性.倘若教材上什么都讲解什么都编写，那就不是教材，而是参考资料或习题集.这就要求教师要认真钻研教材，真正做到用教材教，而不是教教材.