对一道习题的探究

云南省昆明市第三中学 (650500)

农秀权

对一道习题的探究

云南省昆明市第三中学 (650500)

农秀权

1．问题的提出

近年来，很多学生已经体会到了运用空间向量来求解空间立体几何问题的先进性和优越性，而对于运用平面向量解决平面几何问题，虽在教材中已经有展示，但是在解决实际问题中，平面向量的思想方法却很少被运用，为此笔者对此问题做进一步的探究．

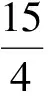
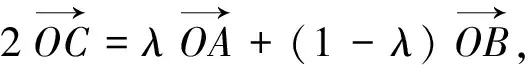
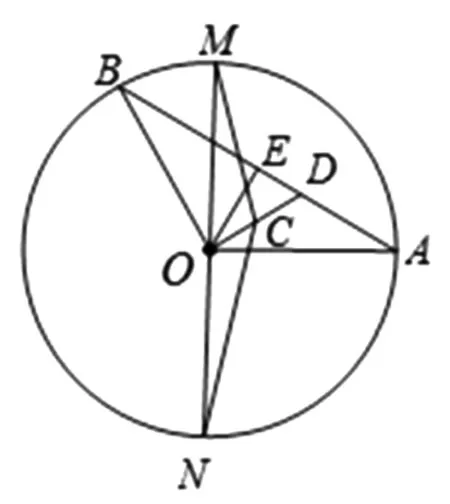
图1

如图1，考虑到CO是ΔMCN的中线，设点E是弦AB的中点．由极化恒等式知

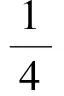
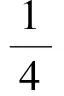
上述题目及解法摘自《数学通讯》2015.1下半月，在文中，作者通过建立平面直角坐标系，运用向量法求解此题．虽已经涉及到向量求解平面几何的问题，但是笔者认为上述解法抓住向量求解平面几何的本质．向量是连接代数与几何的桥梁，如何架起这座桥是很多学生的难点，在此，将给出基本的思想和方法．

2．新的解法

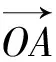
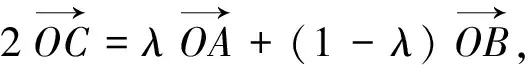
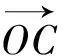
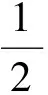
3．对新解法的评析

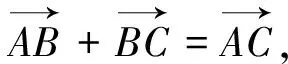
最后，通过向量运算，研究几何元素之间的关系，如证明平行、垂直，求解线段比率，夹角等问题．

向量法可以借助建立直角坐标系的思想方法，但是与建立直角坐标系相比，向量法却又可以解决建立不了或者难以求解坐标点的几何问题，当然并不是说明向量法就比坐标法更优越，有时在研究几何问题中将两种方法结合在一起会取得更佳的效果．

4．进一步应用

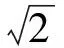
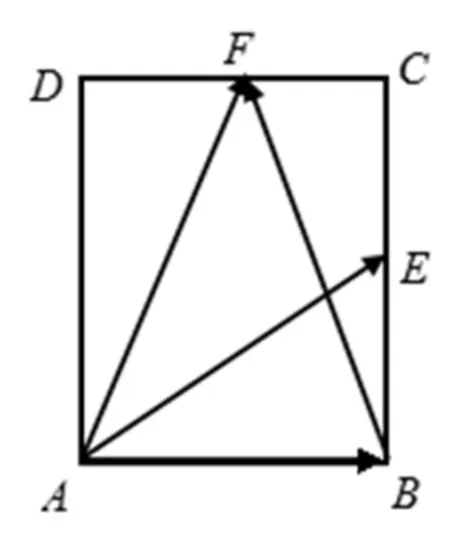
图2

很多资料给出了如下的解答：

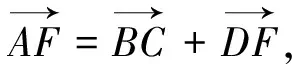
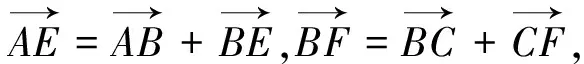
在很多书上已经给出了以上较为简单的方法，虽然很容易看懂，但是没有指导性的思想，当遇到类似的题目，学生仍然无法下手，下面给出以文中提出的思想为指导的解法：

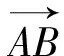
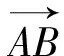
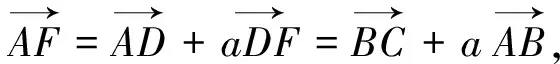
5．结语

在习题的讲解中适时对数学思想方法做出归纳、概括是十分必要的，这样不仅可以使学生从数学思想方法的高度把握知识的本质和内在规律，也使其对运用数学思想解决问题的具体操作方式有更深刻的理解，有利于弄清一些常用的数学思想方法通常应该在哪些场合下应用，如何使用，使用时注意什么问题等．

[1]施刚良．好问题指引，真探究前行[J]．数学通讯，2015，(1)．