以“圆”为背景的取值范围问题的几种转化策略

江苏省江阴市青阳中学 (214401)

石海峰

以“圆”为背景的取值范围问题的几种转化策略

江苏省江阴市青阳中学 (214401)

石海峰

直线与圆有关的问题是江苏高考的重点与难点.其中一类是以“圆”为背景的取值范围问题，从笔者所带班级(物理化学班，在年级中属于数学成绩较好的)的学生做这类题目的情况来看，学生对于这块知识点掌握很不到位.如果教师在授课过程中，能引导学生充分利用“圆”本身图形的特殊性，解题效果必然事半功倍.笔者针对这类问题做了一些研究，总结出以“圆”为背景的取值范围问题的几种转化策略：

一、转化为圆上点到直线的距离的最值问题

圆是最美的图形,既是轴对称图形，又是中心对称图形.圆上的点到直线距离的最大值为圆心到直线距离加上半径长，当直线与圆相离时，最小值为圆心到直线距离减去半径长；当直线与圆相交或相切时，最小值为零.因此可以根据这个性质，求圆上的点到直线距离的最大值和最小值.

例1 (江苏省南京市、盐城市、连云港市2017届高三第二次模拟考试第11题)在平面直角坐标系xOy中，若直线l1:kx-y+2=0与直线l2:x+ky-2=0相交于点P，则当实数k变化时，点P到直线x-y-4=0的距离的最大值为________.

图1

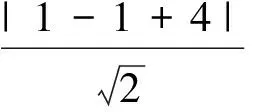
二、转化为定点与圆上动点的距离的最值

定点与圆上的动点的距离也是有范围的，其最大值为定点与圆心的距离加半径长，最小值为定点与圆心的距离减半径长的绝对值，根据圆的这个性质，如果将所求的范围问题转化为定点与圆上点的距离问题，问题将迎刃而解.

例2 已知实数a,b,c满足b+c=2a，直线l:ax+by+c=0，过点P(2,3)作直线l的垂线，垂足为M，O为坐标原点，则线段OM的长度的最大值为________.

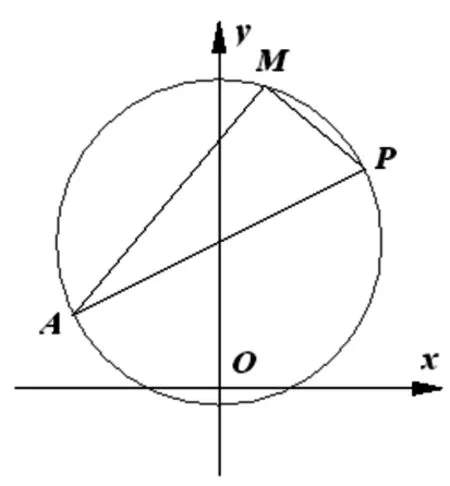
图2

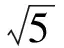
例3 (江苏省南通市、泰州市2017届高三第一次模拟考试第14题)在平面直角坐标系xOy中，已知B,C为圆x2+y2=4上两点，点A(1,1)，且AB⊥AC，则线段BC的长的取值范围为________.

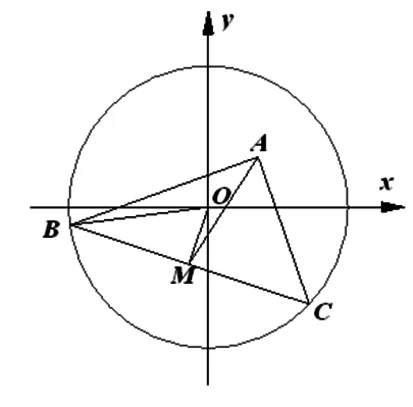
图3

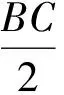
例2和例3两道题都是将所求的范围问题转化为一个定点到圆上动点的距离最值问题，这类题目的关键都是准确的求出动点的轨迹方程，可利用圆上点对直径的张角为90°、垂径定理等来快速求出动点的轨迹方程.

三、转化为两个圆上的动点间的距离的最值

两个圆上的动点间的距离的最大值为两圆的圆心距加上两圆的半径长，当两圆相外离时，最小值为两圆的圆心距减去两圆的半径长；当两圆相交或相切时，最小值为零；当两圆内含时，最小值为大圆半径减去圆心距再减去小圆半径.如果将所求的距离转化为两圆上两动点间的距离，则能够很容易求出取值范围.

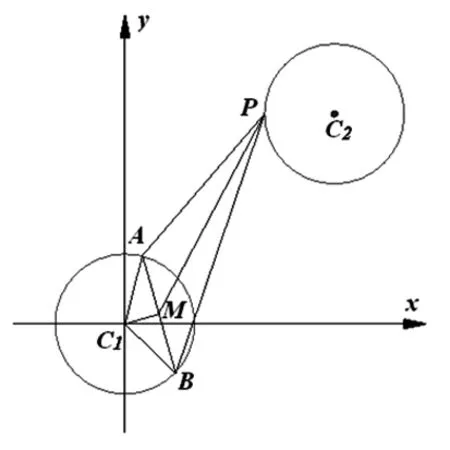
图4

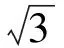
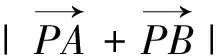
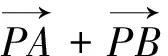
本题中两个关键点：一是平面向量加法的平行四边形法则要比较熟悉，二是涉及到圆中的弦长问题想到用垂径定理解决.这两个关键点都是学生掌握得比较好的，所以不少学生做起来比较顺利.本题将向量的模长取值范围问题转化为两个圆上点间的距离的最值问题，如果学生能实现这一转化，这个取值范围问题就很容易解决.

四、转化为直线与圆的位置关系求最值

直线和圆的位置关系有相交、相切、相离.判断直线和圆的位置关系通常有两种方法：一是“判别式法”：将直线方程与圆方程联立方程组，消元后得到关于x或y的一元二次方程，当判别式Δ>0时，直线与圆相交；当Δ=0时，直线与圆相切；当Δ<0时，直线与圆相离，二是“几何法”：设圆心到直线的距离为d，圆的半径为r，当dr时，直线和圆相离.而这两种方法中，又以第二种方法“几何法”运用的较多.如果确定了直线和圆的位置关系，就可以找出d和r的不等关系，通过不等关系可以找出变量的取值范围.

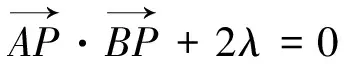
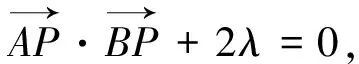
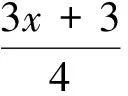
五、转化为圆和圆的位置关系求最值

圆和圆的位置关系有内含、内切、相交、外切、外离.设两圆的圆心分别为O1,O2，两圆的半径为r1,r2，则当O1O2<|r1-r2|时，两圆内含；当O1O2=|r1-r2|时，两圆内切；当|r1-r2||r1+r2|时，两圆外离.因此，如果能将已知条件转化为圆和圆的位置关系，则可找到不等式，求出参数的范围.

例6 (江苏省2013年高考第17题第(2)问)在平面直角坐标系xOy中，点A(0,3)，直线l：y=2x-4.设圆C的半径为1，圆心在l上.若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围.

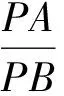
六、转化为其它不等关系找出取值范围

例7 (江苏省连云港市、宿迁市、徐州市2017届高三第三次模拟考试第13题)在平面直角坐标系xOy中，圆C:(x+2)2+(y-m)2=3.若圆C存在以G为中心的弦AB，且AB=2GO，则实数m的取值范围是________.

本题得分率仅有13.6%.很多学生看了这道题就直接放弃，不知从哪里可求出范围，笔者从以下两种思路来分析本题：

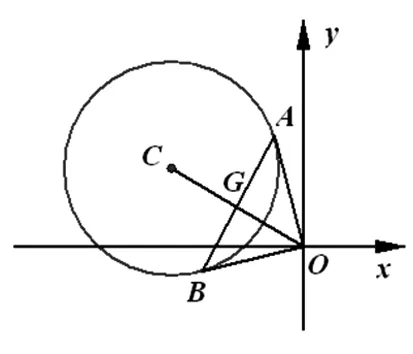
图5

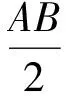
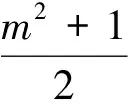
本题可以通过二元二次方程表示圆(或点)的条件、借助临界情况(相切)时找出不等关系，求出参数的范围.

处理参数的取值范围问题关键是找到合理的不等关系.如果能充分运用轨迹思想，利用图形(如“圆”)的特殊性，通过数形结合，找出跟参数有关的不等式，则可简化运算.教师在授课过程中要多与学生探讨、研究，找出问题解决的突破口，寻求问题解决的等价条件，寻找最简捷的途径解决，并养成及时总结的习惯，让学生做一题通一类，从“题海”中解放出来.