单相逆变器分数阶建模及分析*
2017-12-20马冬冬王志强王进君李国锋
马冬冬,王志强,王进君,李国锋
(大连理工大学 电气工程学院,辽宁 大连116024)
0 引 言
逆变器作为一种重要的电力电子变换装置,对其真实系统的精准分析和设计具有重要意义[1]。逆变器理论分析的前提是对实际系统建立准确的数学模型。国内外相关研究已证明电感和电容呈现分数阶特性[2-3],实际的逆变器系统应是分数阶系统。状态空间平均法、离散时域法等对逆变器建模方法[4]均以整数阶微积分理论为基础,未充分考虑电感和电容的分数阶特性,因此所建立的整数阶模型和实际系统存在一定误差。分数阶建模则考虑到相关元件的分数阶特性,可反映实际系统的分数阶特性。分数阶微积分理论研究的不断突破给电力电子建模分析带来了新的途径。文献[5]建立了传输线的分数阶模型,认为分数阶模型可更准确的描述传输线的分布特性。文献[6-7]分别建立了Buck电路和Boost电路的分数阶模型,并分析了CCM模式下整数阶模型和分数阶模型特性分析上的差异。文献[8]分析了分数阶并联RLαCβ的基本特征和规律,指出分数阶并联RLαCβ在设计上有更大自由度和柔性,具有很多新规律和新现象。文献[9]利用分数阶傅里叶变换分析了逆变器的故障诊断,说明分数阶傅里叶变换对逆变器电路的特征提取更有效。文献[10]针对Z源逆变器、电压源逆变器和三相四桥臂逆变器在整数阶传递函数模型的基础上提出了分数阶状态空间模型,将所有极点替换从而获得稳定的、高过阻尼的闭环系统。单相全桥电压型逆变器在开关机理上和Buck电路具有同构性,在单个开关周期内单相逆变器和Buck电路工作原理本质相同,因此同样可以利用分数阶方法对单相逆变器进行分析。本文建立了单相全桥电压型逆变器的分数阶模型,并比较整数阶模型和分数阶模型分析上的差异。
1 单相逆变器分数阶数学模型
由文献[2]可知,分数阶电感和电容的数学模型为:

式中uL为电感电压;iL为电感电流;uC为电容电压,iC为电容电流;α和β分别为分数阶电感和分数阶电容的阶数;并且满足0<α,β<1。
因单相全桥电压型逆变器输出正负半周的对称性,本文只对电压正半周期进行分析,负半周分析方法相同只是输出电压波形极性相反。逆变器的调制方式有多种,其中单极性倍频SPWM调制,逆变桥臂中点输出电压脉冲频率为开关频率的2倍,因此具有良好的输出波形谐波抑制能力,输出波形脉动频率高而开关管损耗并不增加等优势而被广泛采用。单相逆变器的主电路拓扑结构如图1(a)所示,VT1~VT4为开关管,D1~D4为开关管反并联二极管,L、C为滤波电感和电容,RL为滤波电感寄生电阻,Ro、Lo为负载电阻和电感。在逆变桥臂中点输出电压脉冲单个周期内均有两种工作模态如图1(b)和图1(c)所示,由于单极性倍频SPWM调制的对称性,其他周期原理相同。取电感电流iL、电容电压uC(uC=uo)和负载电流io作为状态变量,组成三维状态向量x=[iL,uo,io]T;udc作为输入变量,组成一维输入向量 u=[udc],电感电流iL和输出电压uo作为输出变量,组成二维输出向量y=[iL,uo]T。根据基尔霍夫定律,对不同工作模态下的电路进行列写状态方程如公式(2)所示。
工作模态1:令占空比为d,单极性倍频SPWM调制下在每一个开关周期Ts的(0,dTs)时间段内,VT1和VT4导通,列写状态空间表达式如下:

式中:
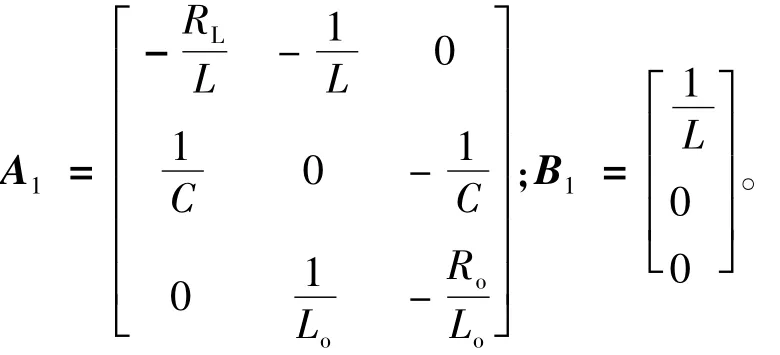

图1 单相逆变器主电路及两种工作模态拓扑Fig.1 Topology of single phase invertermain circuit and two workingmodes
工作模态2:在每一个开关周期Ts的(dTs,Ts)时间段内,电感电流经过D2和VT4续流。列写状态空间表达式如下:

式中:

2 单相逆变器分数阶小信号模型
2.1 状态平均
为了简化模型,需要消除各变量的高频开关纹波分量,利用小纹波假设[11],对变量在一个开关周期内求平均值为:

式中Ts为开关周期。
同理也可以定义平均输入变量〈u〉Ts和平均输出变量〈y〉Ts,求平均状态变量对时间的导数为:

式中γ为分数阶阶数且0<γ<1。
整理可得:

2.2 求取静态工作点
与DC/DC变换器不同,逆变器工作在静态时输出电压按正弦规律变化。但是,当输出电压达到峰值时最容易发生波形畸变,如果能控制好峰值点处的输出电压特性,那么整个频段内输出电压波形畸变都会很小[12]。因此,本文选交流输出电压峰值点作为静态工作点。根据电感电流的伏秒平衡和电容电压的安秒平衡原理有 dγ〈x〉Ts/d tγ=0,代入式(6)得:

式中X是状态变量x的直流分量;U是输入变量u的直流分量;D为静态工作点占空比。
求解式(7)可以得到状态变量的静态工作点的状态空间表达式,即:
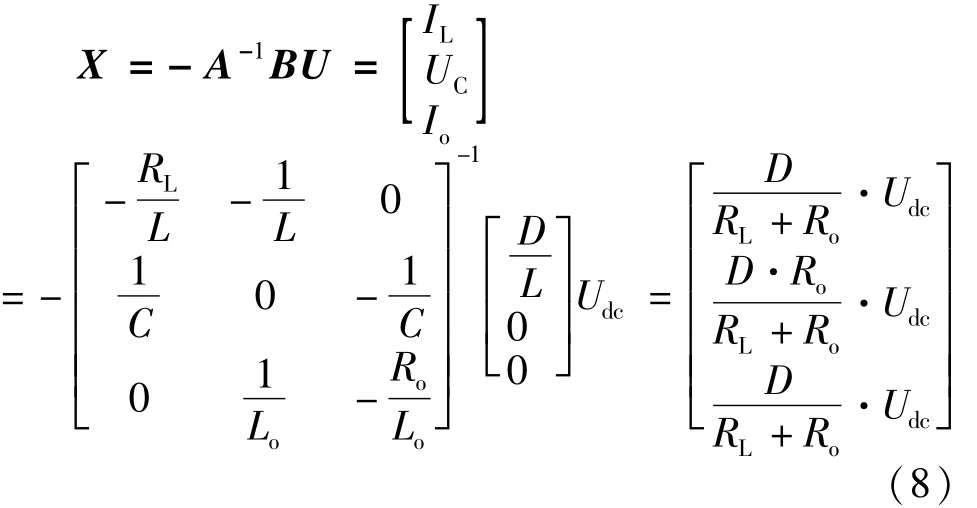
利用Matlab/Simulink搭建1 kW单相全桥电压型逆变器带阻感负载的仿真电路,其参数为:开关频率为10 kHz,直流母线电压udc为400 V,输出电压uo为220 V/50 Hz。调制比是逆变器设计的一个重要参数,为逆变器输出电压基波幅值与直流母线电压之比,调制比主要影响逆变器的直流电压利用率和输出电压波形谐波[13],综合二者选择一个最优点,本设计选择调制比为0.78。将逆变器的参数代入式(8)得到峰值点处值即静态工作点各变量的值如表1所示。

表1 逆变器输出电压峰值点处的值Tab.1 Value of inverter in the output voltage peak point
2.3 分数阶小信号等效电路
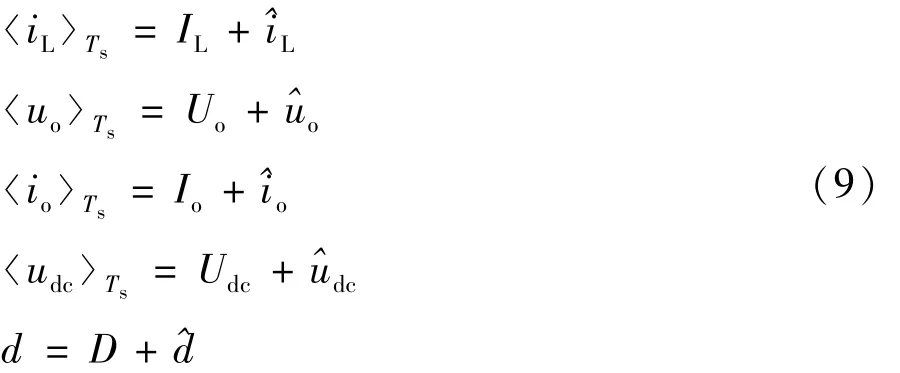
将式(9)代入式(6)可得:


将 A1、A2、A、B1、B2、B代入式(11)可以得到单相逆变器的小信号状态空间表达式为:

由式(12)可画出单相逆变器小信号等效电路,如图2所示。
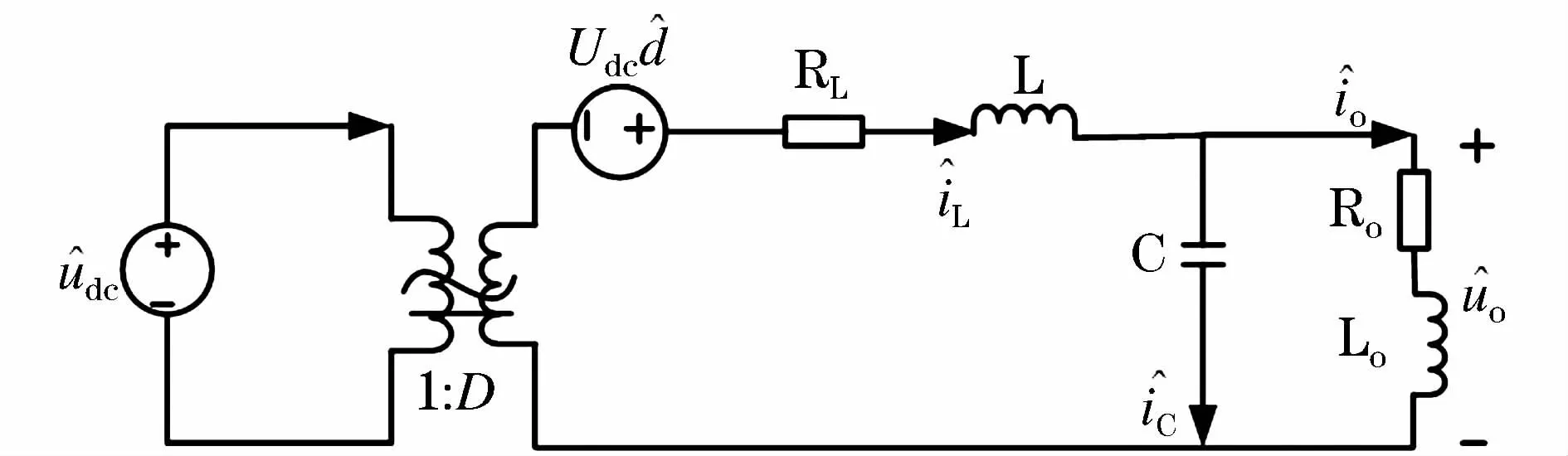
图2 逆变器小信号等效电路Fig.2 Inverter small-signal equivalent circuit
利用基于分数阶微积分的拉普拉斯变换方法[14]对式(12)进行变换得到式(13),可求出占空比至输出电压的传递函数如式(14)所示。

电压型逆变器,输出电压与负载无关,因此常选择输出电压作为被控量,更易于控制。由占空比至输出电压的传递函数可以进行逆变器开环稳定性和动态特性进行分析。
2.4 Matlab数值分析
根据参考文献[14]中对分数阶微积分的计算机求解方法及Oustaloup算法,利用Matlab软件对分数阶微积分算法进行编程来建立分数阶传递函数类fotf,从而构建分数阶传递函数。在@fotf目录下重载函数bode.m和step.m来画出分数阶传递函数的Bode图和阶跃响应曲线。还可以利用Simulink中的模块封装技术构建分数阶传递函数模块。
通过式(14)可以看出占空比至输出电压的分数阶传递函数与分数阶电感和电容的阶数有一定关系。因此分数阶电感和电容的阶数无论是在频域还是时域都会影响到系统的性能。
根据分数阶系统的Bode图和阶跃响应定义的计算,令分数阶电容的阶数β=1.0时,取分数阶电感阶数α为不同值时占空比至输出电压的分数阶传递函数的Bode图和阶跃响应如图3所示,令分数阶电感的阶数α=1.0,取分数阶电容的阶数β为不同值时占空比至输出电压的分数阶传递函数的Bode图和阶跃响应如图4所示。

图3 β=1时不同α值时Gud(s)的Bode图和阶跃响应Fig.3 Bode plots and step responses of Gud(s)for differentαandβ=1

表2 β=1时不同α值时逆变器的性能指标Tab.2 Properties index of inverter for differentαandβ=1
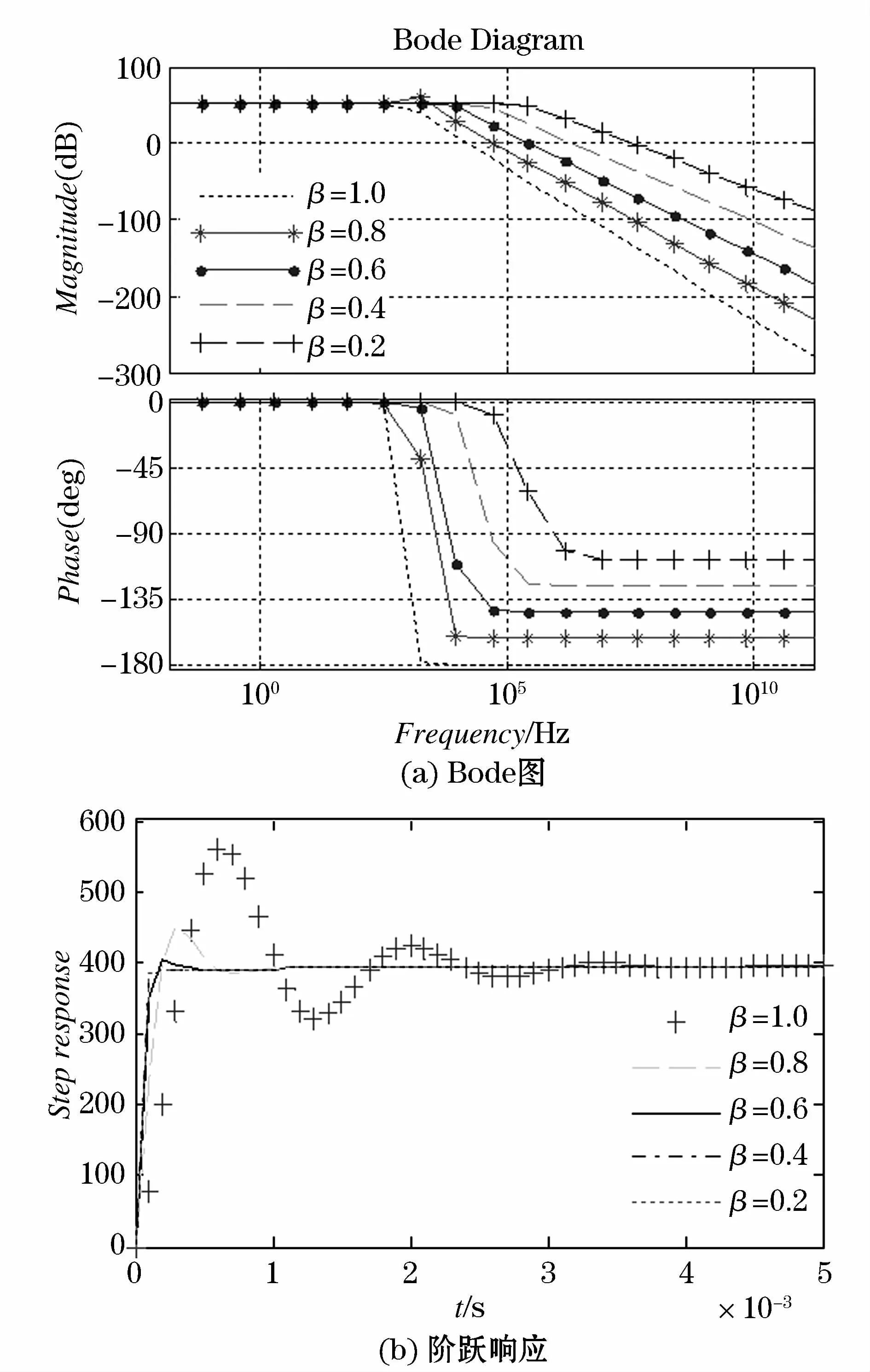
图4 α=1时不同β值时Gud(s)的Bode图和阶跃响应Fig.4 Bode plots and step responses of Gud(s)for differentβandα=1
从图3和图4中可以得出的逆变器性能指标参数如表2和表3所示,随着α和β值的增加逆变器相角裕度不断减小,α,β≤0.4时相角裕度大于45°系统稳定性较好,而α,β>0.4时相角裕度小于45°系统稳定性较差;随着α和β值的增加阶跃响应的上升时间、峰值时间、调整时间和超调量都在不断的增大,动态特性变差。因此,可以得出利用不同阶数的分数阶电感和电容建立的逆变器分数阶小信号模型分析得出系统的稳定性和动态性能存在很大差异,当α=1和β=1时建立的是整数阶模型,这种差异会随着分数阶阶数偏离1的距离增大而增大。由于实际的电感和电容的分数阶阶数均小于1,通过建立的分数阶模型来分析系统稳定性和动态性能更准确地设计补偿器。

表3 α=1时不同β值时逆变器的性能指标Tab.3 Properties index of inverter for differentβandα=1
3 电路模型仿真
3.1 分数阶电感和电容的等效电路模型
在复频域内将分数阶微积分用Oustaloup算法近似,然后对高阶整数阶传递函数进行部分分式展开,最后将各个部分进行串联或并联,即可构造出分数阶系统等效电路。对于分数阶电感和电容利用相同的方法得到的电抗称为分抗链[15],如图5所示为0.8阶的分数阶电感和电容的等效模型。

图5 分抗链Fig.5 Chain fractance
3.2 分数阶与整数阶电路模型仿真比较
根据单相逆变器分数阶小信号模型,基于Matlab/Simulink及框图分数阶仿真分析方法[16],建立单相逆变器开环系统数学模型如图6所示,其中2/V M为PWM调制器模型。
利用分抗链原理建立分数阶电感和电容的电路等效模型,从而搭建单相逆变器分数阶电路模型如图7所示,其中的无源滤波LC分别采用分数阶电感和分数阶电容的分抗链模型,阶数均取为0.8阶。

图6 单相逆变器开环数学模型框图Fig.6 Open-loop mathematic model block diagram of single phase inverter
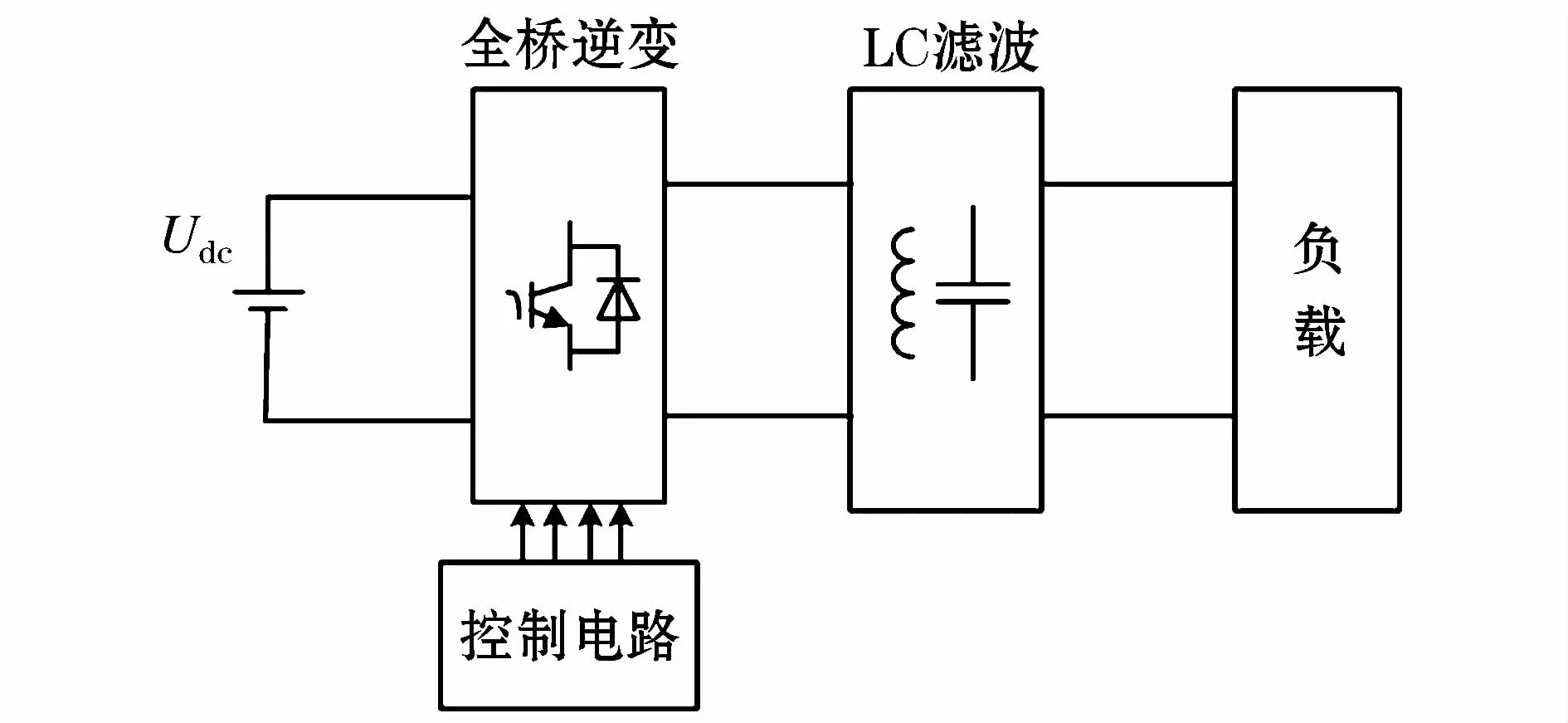
图7 单相逆变器分数阶电路模型Fig.7 Fractional circuitmodel of single phase inverter
对输出电压的理论计算和电路模型仿真结果对比如图8所示可知:整数阶模型与理论计算输出电压偏差最大可达9.38%,而分数阶模型与理论计算输出电压偏差最大为1.56%,和整数阶模型相比分数阶模型与实际系统的偏差要小很多,因此利用分数阶模型能更好的接近实际系统。

图8 逆变器输出电压波形Fig.8 Output voltage waveforms of inverter
4 结束语
本文将国内外学者提出的分数阶微积分理论应用到了单相逆变器建模中,得出以下结论:
(1)由单相逆变器分数阶小信号模型得到的占空比至输出电压的传递函数中含有分数阶电感和分数阶电容。因此,通过理论计算所得传递函数的Bode图和阶跃响应分析以及利用Matlab/Simulink软件电路模型仿真结果表明单相逆变器的稳定性和动态性能和分数阶电感和电容的阶数有关;
(2)利用逆变器分数阶小信号模型和整数阶小信号模型来分析逆变器性能会得到不同的结果,分数阶模型更接近实际系统。
