基于灰靶决策和NSGA-II的配电系统分布式电源多目标优化

谢青洋，王韶，邓先芳，张成瑜，苏适

（1.云南电网有限责任公司电力科学研究院，昆明650217；2.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆400044）

0 引 言

随着能源危机和环境问题日益严重，分布式电源（Distributed Generation，DG）因具有发电方式灵活、投资成本低、产生污染少等特点受到越来越多的关注。合理配置DG可以有效减少网络损耗、缓解电网升级改造、提高电能质量。但由于DG的出力具有随机性和间歇性，若配置不合理，反而会给电网带来不良影响［1］。因此有必要研究DG的合理配置［2］。

DG的合理配置是一个多目标优化问题。文献［3-13］分别考虑投资运行成本、网损、电压偏差、电压稳定性、切负荷量、环境效益、污染气体排放、DG出力最大、电压暂降损失、电量不足期望值、DG年寿命周期收益率等因素建立了DG合理配置的多目标优化模型。

对建立的DG配置多目标优化模型可采用线性加权方式将其转化为单目标模型求解，但各目标的权重不易确定。采用多目标方法求解可以避免这一问题。文献［3-6］和文献［7-11］分别采用多目标粒子群优化算法和带精英策略的非支配排序遗传算法（NSGA-II）求解建立的DG配置多目标模型。文献［12-13］分别采用非劣排序复合微分进化算法和快速非支配萤火虫优化算法求解建立的多目标模型。

用多目标方法求解DG配置的多目标优化模型得到的结果是一个Pareto解集，需通过“选优”从中找出一个最接近理想方案的最优解。常用的“选优”方法有模糊综合评价法［3，5，8，11-13］。但是该方法依赖于专家的评判信息，具有较大的主观性。

针对这一问题，文中提出采用利用客观数据的信息熵赋权法和灰靶决策在Pareto解集中选出最优解。首先在对DG和负荷的概率模型进行拉丁超立方抽样得到DG出力和负荷功率的基础上，从电压质量和经济性两个方面建立多目标数学模型。其次运用NSGA-II算法求解建立的模型得到Pareto解集。然后采用基于信息熵赋权的多目标灰靶决策算法选出最优方案。最后用仿真算例说明本文方法的有效性。

1 风电、光伏出力和负荷的多状态场景

为计及风机、光伏出力和负荷的不确定性，根据已有研究，文中假定规划阶段的风速和光照强度，以及负荷分别服从 Weibull分布和Beta分布［14］，及正态分布［1］，其概率密度函数如下：

式中v为实际风速；k和c分别为形状参数和尺度参数；r和rmax分别为实际光照强度和最大光照强度；α和β分别为形状参数；P为有功负荷；μ和σ分别为数学期望和标准差。

风机出力与风速和光伏出力与光照强度的关系如下：

式中 PW，n和 PP，n分别为风机和光伏的额定出力；vci、vn、vco分别为风机的切入风速、额定风速和切除风速。

本文采用拉丁超立方抽样［15］对风速、光照强度和负荷的概率分布进行抽样，抽样过程中用式（4）和式（5）将风速和光照强度转换为风电和光伏出力从而得到风电出力、光伏发电出力和负荷的多状态场景。

2 DG选址定容的数学模型

借鉴已有文献的模型［3－13］，文中基于风机和光伏发电的出力及负荷的多状态场景，以节点电压总偏差、DG投资运行维护费用、网损费用和购电费用为目标函数最小建立DG选址定容的多目标数学模型。具体的目标函数为：

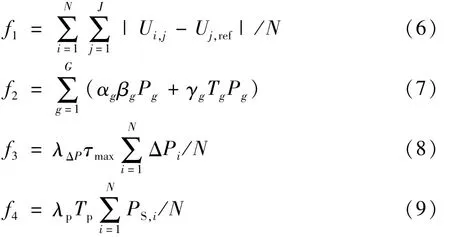
式中 N为抽样次数；J为节点总数；Ui，j为第i次抽样状态下节点j的电压幅值；Uj，ref为节点j的期望电压幅值；G为接入 DG的节点总数；αg、βg、Pg、γg和 Tg分别为节点g处接入DG的固定投资平均年费用系数、单位造价、额定容量、单位运行维护年费用和运行时间；λΔP为单位电能损耗费用；τmax为最大负荷损耗时间；ΔPi为第i次抽样状态的有功损耗；λp和Tp分别为单位购电费用和购电时间；PS，i为第i次抽样状态下电源变电站出线的总有功功率。

约束条件包括功率平衡约束、节点电压约束、支路容量约束、DG接入总容量约束，具体如下：

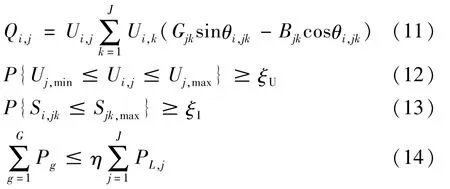
式中 Pi，j和 Qi，j分别为第 i次抽样状态下节点 j的注入有功和无功；Ui，j和 Ui，k分别为第 i次抽样状态下节点j和k的电压幅值；θi，jk为第i次抽样状态下节点j和k之间的电压相角差；Gjk和Bjk分别为节点j和k之间的电导和电纳；Uj，max和 Uj，min分别为节点 j的电压幅值上下限；ξV为节点电压幅值的置信水平；Si，jk为第i次抽样状态下支路jk的功率；Sjk，max为支路jk的功率上限；ξI为支路功率的置信水平；PL，j为节点 j的有功负荷；η为DG的渗透率。

3 DG选址定容模型的求解

文中基于NSGA-II［16］算法实现对建立的DG选址定容数学模型的求解。算法的流程如图1所示。

采用十进制对种群中的染色体进行编码。染色体 X＝{x1，x2，…，xj}，xj的取值范围为{0，1，2，…，Gj}，其中Gj为节点j安装的DG的额定容量种类，0表示节点j不安装DG，其它数字表示不同的DG额定容量。

在图1中设置修复不满足总容量约束的不可行解计算步骤是由于在产生初始种群或进行交叉和变异形成新种群时，染色体可能不满足式（14）的约束。文中提出的将不可行解修复为可行解的策略如下。

（1）从染色体X中取出非零元素形成数组X1；

（2）计算X1对应的DG额定总容量。若DG额定总容量满足式（14）约束条件，则结束修复。否则令 PgΣ＝0；转至步骤（3）；

（3）从X1中随机选出一个元素k，将其对应的DG额定容量加入PgΣ中，并从X1中删除元素k得到新的 X1。若 PgΣ满足式（14）约束条件，转至步骤（3）；否则，减少元素k对应的DG额定容量直到PgΣ满足式（14）约束条件；

（4）将X中对应于元素k的位置的编码修改为此时的元素k，并将X中对应于此时的数组X1中的所有元素的位置的码修改成0。

在计算目标函数前，先对DG出力和负荷进行抽样形成其多状态模型；然后对每一抽样状态进行潮流计算；在潮流收敛条件下，判断是否满足式（12）和式（13）的约束条件。对满足条件的状态按照式（6）～式（9）计算目标函数值，否则将目标函数值置一大数作为惩罚。图1算法的进化过程结束后得到一个DG优化配置的Pareto解集。

图1 基于NSGA-II的DG多目标优化算法流程图Fig.1 Algorithm flow chart formulti-objective optimization of DG based on NSGA-II

4 基于熵权法的灰靶决策选择最优方案

从Pareto解集中优选出最优解是一个多目标决策问题。灰靶决策［17］是灰色系统理论中解决多指标决策问题的方法之一，可用于优选最优解。灰靶决策用客观数据确定理想方案作为靶心，通过计算待选方案与理想方案之间的靶心距得出最优方案。其中可用熵权法得到基于客观数据计算各评价指标的权重确定靶心距。由于信息熵赋权法和灰靶决策不依赖专家的评判信息，能充分利用客观数据提供的信息确定客观权重和各个方案与最优理想方案的接近度，避免主观性的影响，因此文中采用该方法从Pareto解集优选DG选址定容方案。

4.1 确定灰靶靶心

首先，将Pareto解集的第i个待评估方案中第j个目标函数值记为 xij（i＝1，2，…，m；j＝1，2，…，n），从而形成初始效果样本矩阵 X0＝（xij）m×n。

然后，将效果样本矩阵X变换为决策矩阵R＝（rij）m×n。对目标函数 j＝1，2，…，n，若 j为成本型，rij＝（zj-xij）/rmax；若 j为效益型，rij＝（xij-zj）/rmax；若 j为区间型（包括固定型指标），令 xij＝｜xij-zj｜，将其转化为成本型。其中：

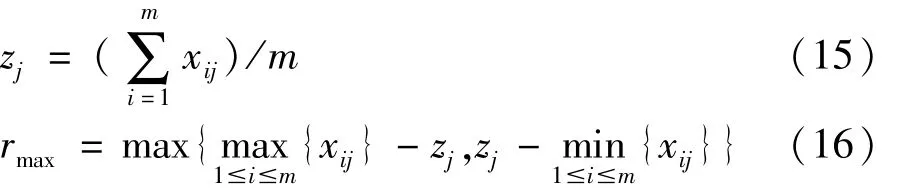
最后，确定目标函数的多指标灰靶决策的靶心向量 r0＝（r1j）1×n，r0的元素为：

4.2 计算靶心距

靶心距反映各方案的优劣程度。靶心距越小表示方案越接近理想方案，即该方案越优，反之亦然。因此，靶心距最小的方案即为最优方案。

设 ri＝{ri1，ri2，…，rin}为方案 i的效果向量。方案 i的靶心距为 di＝｜ri-r0｜，即：

式中 wj（j＝1，2，…，n）为各目标的权重。权系数的大小体现了指标j对决策的影响程度。

文中采用熵权法确定式（18）的权重。

首先将初始效果样本矩阵标准化。第i个待评估方案中第j个目标函数值xij的标准化值为：

然后计算各目标函数的熵值Ej为：

其中，当 yij＝0时，令 yijln yij＝0。

最后计算各目标函数评价指标的熵权。

5 仿真分析

采用图2所示的25节点配电网［18］作为算例。该配电网的电压等级为10 kV，有1个电源节点，24个负荷节点，总负荷为2 295 kW。

不失一般性，假设节点13、15和18可安装风机，节点10、21和25可安装光伏。风机和光伏发电的额定容量均分别为0 kW、200 kW、250 kW、300 kW、350 kW、400 kW；风机和光伏的固定投资平均费用系数为0.05，单位造价分别为1.3万元/kW和4.55万元/kW，单位运行维护年费用为0.39元/kWh和1.61元/kWh；运行时间和购电时间均为8 760 h；单位网损费用为0.4元/kWh；最大负荷损耗时间为3 000 h；单位购电费用为0.33元/kWh；各节点期望稳态电压幅值均为1 p.u.；电压上下限分别为1.07 p.u.和0.93 p.u.；电流置信度和电压置信度均设为0.8；DG渗透率为25%；风速服从Weibull分布，参数k和c分别为2.3和8.92；光照强度服从Beta分布，参数α和β分别为0.85和0.85；负荷为正态分布，方差为0.1 kW2。计算时，基准电压和容量分别取为10 kV和10 MVA；LHS抽样次数为100；迭代次数为100；种群大小为100。

图2 某配电网算例Fig.2 Calculation example for a distribution network

利用文中的方法进行仿真计算，由图1的算法可得到的Pareto解集。在删除该解集中重复的方案后，表1给出了Pareto前沿的10个方案，据此可选择DG的配置方案。

由表1很容易排除方案1～5。这是因为方案1的节点电压总偏差最大，方案5的网损费用和购电费用最大，而方案2～4的DG投资运行维护费用至少是其他方案的2倍以上。方案2～4的DG投资运行维护费用较高的原因是，这些方案在节点25安装了单位投资运行维护费用较高的光伏发电。

决策者可以根据自己的偏好在方案6～10中选择DG配置方案，然而仅凭直观感觉难以确定最优的选址定容方案。这是因为方案6～10均在节点13和15安装风电机组，各方案的目标函数值的差异不明显，而且存在着矛盾不一致的目标函数值。例如，方案6的节点电压总偏差比方案7的小，但方案6的投资运行维护费用比方案7的大。

表1 不同方案的DG优化配置结果Tab.1 The results of the optimal DG configuration under different schemes

文中采用基于熵权法的灰靶决策方法选出的最优方案为方案7。由表1可见，在方案6～10中，尽管方案7的网损费和购电费最大，但与其他方案相差并不大，而方案7配置的DG容量最小，因此其总费用最小，为823.26万元。在表1的方案6～10中，方案7的电压总偏差也最大，但由于这些方案安装DG的位置相同，不同的仅是选择在节点13安装200、300 kW或350 kW、在节点15安装200 kW或250 kW的DG容量的差异。因此就DG对网络中每个节点电压改善的效果看，方案7相对于其他方案并无明显差异。图3给出了没有装设DG和方案6～10的节点电压分布。由图3可见，各方案的节点电压相差不大，但均较无DG时的节点电压有明显改善。可见，基于熵权法的灰靶决策方法选出的最优方案是合理的。

图3 不同方案的节点电压Fig.3 Node voltage under different schemes

6 结束语

本文针对从DG优化配置多目标模型的Pareto解集中选优最优解问题，提出采用信息熵赋权法和灰靶决策确定最优方案。首先基于DG出力和负荷的多状态场景，以节点电压总偏差、DG投资运行维护费用、网损费用和购电费用为目标建立多目标模型。然后采用NSGA-II算法求解该模型得到Pareto解集。最后采用基于熵权法的灰靶决策方法确定最优方案。仿真算例表明基于熵权法的灰靶决策方法能够在各方案目标函数值的差异不明显情况下选出最佳方案，为决策提供依据。该方法可避免主观信息对规划结果的影响，使结果更加客观，同时还具有方法简便和易于实现的特点。