模块化多电平变换器最近电平调制研究*
2017-12-20张国荣韩慧颖王啸飞陈祥
张国荣,韩慧颖,王啸飞,陈祥
(1.合肥工业大学电气与自动化工程学院,合肥230009;2.芜湖县广播电视台,安徽芜湖241199)
0 引 言
模块化多电平变换器(MMC)因其在功率控制、开关频率、输出波形、模块化设计等方面的诸多优点在高压大功率场合得到了广泛应用。目前针对MMC相关技术的研究主要包括数学模型、环流抑制、调制技术以及电容电压平衡等方面[1-2]。调制策略作为其中的关键技术之一,直接影响到 MMC运行的性能。
现阶段已有相关文献对MMC的最近电平调制方法展开不同程度的研究。文献[3]结合谐波水平、开关频率、直流电压利用率几个主要衡量指标综合比较了MMC采用不同调制策略时的特性,指出最近电平逼近调制在MMC实际应用中电平数较多时切实可行,其他调制策略则具有各自不同的应用场合特征。文献[4]分别对载波移相调制和脉冲移相调制的原理进行了分析和仿真,并通过样机实验验证,说明了两种调制方法各自的优缺点。文献[5]推导出NLM基波和各次谐波的解析表达式,并验证了最近电平调制在MMC中良好的调制波跟踪能力。近年来提出了一种基于排序算法的电容电压平衡控制的最近电平调制[6-7],针对开关频率问题对电容电压平衡进行控制,以抑制电路环流。文献[8]在考虑子模块电容电压波动的条件下,从优化电容电压均衡策略的角度出发,提出一种改进最近电平调制策略的控制方法,抑制直流电压波动以及对二倍频环流进行控制。文献[9]提出了一种取整修正量移位算法,进一步抑制桥臂输出电压的畸变。文献[10]提出一种改进型调制方法,其效果接近载波移相与改进型模块统一PWM方法,但仅考虑了一种典型值,未对各种综合情况进行分析比较。文献[11]提出了一种改进的最近电平调制方法,通过增加一个小的二倍频电压偏移量来提高MMC输出电压质量。
本文首先阐述了传统最近电平调制方法的基本原理,对传统调制方法进行改进,结合电容电压平衡控制策略,在上、下桥臂输出电压电平相同的基础上,对近似函数进行相关处理,显著提高交流侧输出电压特性,同时分析总结出上、下桥臂输出的最优近似函数组合,最后进行仿真验证。
1 MMC基本原理及数学模型
1.1 MMC基本原理
如图1(a)所示模块化多电平变换器的基本结构,包括三个完全相同的相单元,每相均包括上桥臂和下桥臂,每个桥臂由N个结构相同的子模块(Sub-Module,SM)以及一个限流电抗器组成,再与交流侧相连。子模块为上管T1和下管T2以及直流电容C组成的半桥结构,如图1(b)所示,T1包括功率管VT1与其反并联二极管D1,T2包括功率管VT2与其反并联二极管D2。
图1中,O为参考0电位,Udc表示直流侧电压,L、C分别表示桥臂串联电抗器及子模块电容,子模块电容电压用Uc表示。正常工作时,MMC的子模块工作在投入状态或切除状态。子模块投入时,上管为开通而下管为关断状态;子模块切除时,而上管为关断而下管为开通状态。此外,在启动和故障时,子模块还存在一种管子全部关断的状态-闭锁状态[12]。子模块开关管的状态组合与桥臂电容的充放电状态关系如表1所示。
表1中,1表示开关管为开通状态,0表示开关管为关断状态。ism>0表示子模块充电,ism<0表示子模块放电。Uc0为子模块电容额定电压。
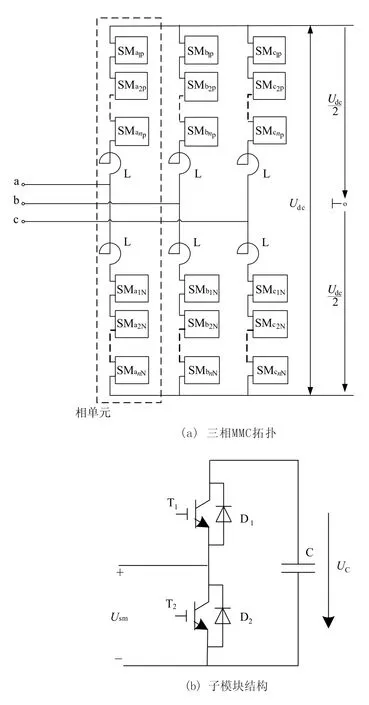
图1 MMC基本拓扑Fig.1 Basic topology of MMC

表1 子模块开关管开关状态Tab.1 Switch states of the switch tubes in one sub-module
1.2 MMC数学模型
正常工作时,由以上分析可知在两种电流方向下,每个子模块电压有Uc和0两种情况。一般情况下,为稳定直流侧输出电压,要求每相桥臂投入的总的子模块个数一定,且上下桥臂互补投入[13-14]。以a相为例,电压电流正方向如图2(a)所示。正常运行时,由基尔霍夫定律可以列出MMC电压方程满足:

式中 UPa、UNa、iPa、iNa分别为上、下桥臂电压、电流;L为桥臂限流电感;Ua为交流输出相电压;R为桥臂等效电阻。
并且有:

式中ia为交流侧电流。
由式(1)~式(3)整理可得:

势幅值,不妨设ea=eam·sinωt,整理得:
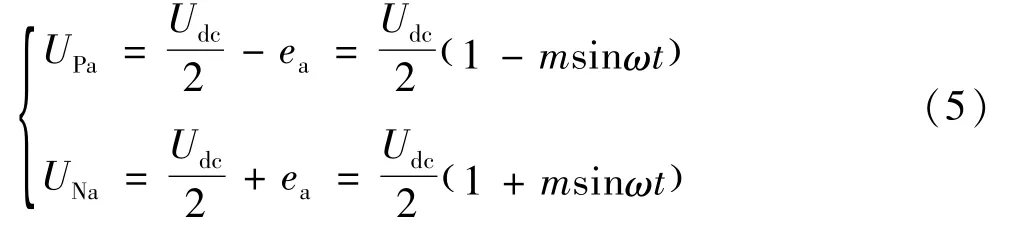
不考虑冗余,根据传统的最近电平调制,任意时刻投入N个子模块[5],直流电压满足:

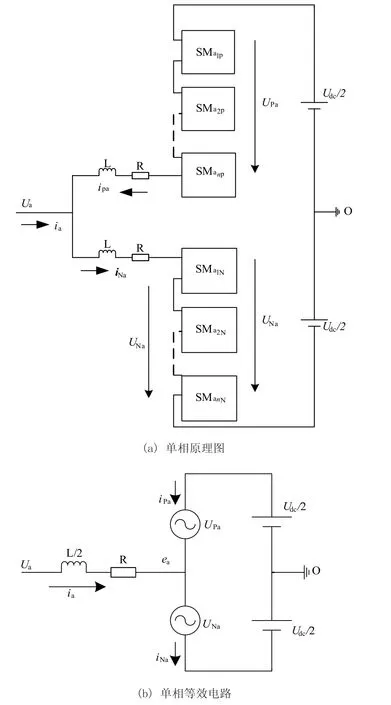
图2 MMC原理图与等效电路Fig.2 Principle diagram and equivalent circuit of MMC
2 MMC的最近电平调制原理
2.1 传统最近电平调制原理
通常情况下,MMC每相桥臂投入的子模块总数不变,但上下桥臂子模块投入存在多种组合。最近电平调制(NLM)的思想是利用阶梯波来逼近正弦波,控制各时刻子模块上下管的触发信号,从而控制相应子模块的投入与切除,使得每一时刻投入n个SM,进而输出n+1电平的电压,以阶梯波来代替正弦波[15]。当子模块数较多时,调制出的阶梯波就越来越接近正弦波。由第二部分可知上下桥臂的参考电压分别为:
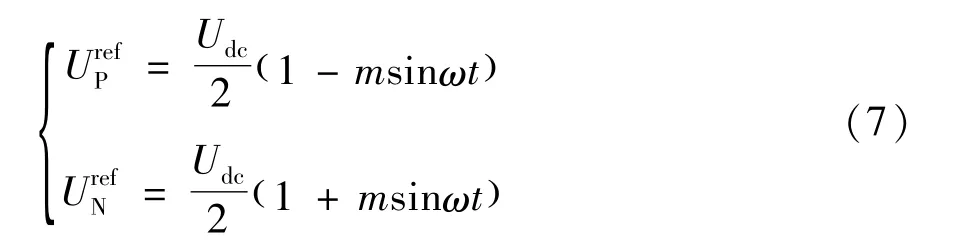

图3为传统最近电平调制的基本框图。

图3 传统最近电平调制(NLM)控制框图Fig.3 Control block diagram of traditional nearest levelmodulation(NLM)
根据式(8)可知各个时刻上、下桥臂处于投入状态的SM数的参考波形,用round函数取整,近似得到不同时刻上、下桥臂实际应投入的SM数目。近似后的波形为阶梯波。结合子模块均压控制,对SM电容电压进行排序,按照桥臂电流的正负,得到各个SM的投切状态以及各自的触发信号。当电容充电时,触发电压较低的n个SM投入,放电时触发电压较高的 n个 SM投入[5,9]。
2.2 改进最近电平调制原理分析
此时,由于上桥臂与下桥臂的调制信号对称,上、下桥臂阶梯波的上升和下降时刻一致,在交流侧能够得到N+1电平的电压波形输出,同时可以得到近似波形和参考波形之间的最大误差为 Uc0/2[10]。N=10时,通过对输出电压波形进行FFT分析可得传统NLM调制下输出电压的THD为7.58%。

图4 传统最近电平调制原理Fig.4 Principle of traditional nearest levelmodulation
当SM数目较少(即N值较小)时,输出电压波形为N+1电平,THD值较大,波形质量较差[16]。为了弥补NLM在N较小时输出电压质量的不足,在相同的桥臂子模块数下,对调制发波的过程进行修正,调整近似算法,使输出电平数由N+1增加至2N+1,提高输出波形质量。
对式(8)进行分析可知,上、下桥臂子模块组调制波对称[8-9],利用NLM方法进行电平逼近时,上下两组波形阶梯产生时刻相同。当控制上、下桥臂阶梯生成时刻,使其不再同步,输出将在两桥臂阶梯波的每一阶梯变化时刻产生阶梯,从而使得交流侧输出的电压由原来的N+1电平增加到2N+1电平,达到接近电平翻倍的效果,波形质量明显提高。
设Δ为round函数自变量的偏差值,且0<Δ<0.5。以 round(x+Δ)来取代 round(x)进行调制。根据最近电平调制基本原理:

式中ΔP、ΔN分别为上下桥臂给定的偏差值。
以ΔP=ΔN=0.2为例,图5为各个时刻上桥臂、下桥臂投入的SM数目的参考值和波形,同时近似后对应的SM实际投入数波形分别为以及交流输出的虚拟电动势波形e。设t1-时刻下桥臂阶梯值为n0,则在t1+时刻,上、下桥臂投入的SM数目与虚拟电动势相应的模块数参考值满足:

同理,t2时刻有:

t3时刻有:
提供的寝室文化方案设计以环保和安全为前提,在遵守学校的各项规章制度下开展寝室设计和打造。装扮以环保贴纸为主,墙贴纸具有易移动粘贴方便的优点,并且也不会破坏墙面的原貌。同时,墙贴纸内容丰富,花色多样,表达主题形象鲜明(如:地中海风格、欧美风格、普普风格、古朴风格等等)。也可根据同学的要求绘画,例如:灯开关旁萌萌的卡通图提醒我们节约用电。在墙纸上绘出室友图形,另外也可根据同学的需求打印3D照片作为墙纸;也可通过挂件、摆饰等更充分地体现出一个寝室的主题。
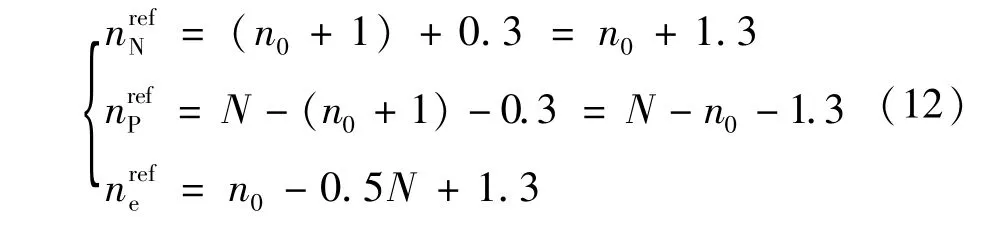
而t1、t2及 t3时刻 NLM调制输出的阶梯数(t)分别为:

由式(10)~式(13),调制函数偏差值为ΔP=ΔN=0.2时,相比传统NLM调制,加入偏差值的改进算法在之前的两次相邻阶梯变化时刻之间,还产生一次阶梯的变化,t1、t2、t3时刻,计算实际阶梯波与参考值的误差,可知改进算法输出的误差分别为0.3、0.2、0.3,最大为0.3。而传统算法的最大误差为0.5,输出波形质量有所改善。
同样,可得ΔP=ΔN=0.2,N=10时改进算法输出的虚拟电动势波形,对其进行FFT分析,包含THD的结果如图6所示。

图5 ΔP=0.2,ΔN=0.2上、下桥臂投入子模块数及虚拟电动势输出波形Fig.5 Number of sub-modules of upper and lower bridge arm and outputwaveform of virtual electromotive force inΔP=0.2,ΔN=0.2

图6 ΔP=0.2,ΔN=0.2虚拟电动势输出及FFT分析Fig.6 Outputwaveform of virtual electromotive force and FFT analysis inΔP=0.2,ΔN=0.2
可以看出,近似函数中加入调制偏移量Δ后,交流侧得到的虚拟电动势波形的阶梯数变为2N+1,THD值下降。以N=10来看,改进前后THD值由7.58%下降至4.11%。若桥臂串联的SM数目N增大,改进NLM方法波形改善的效果将更加显著。文献[12]讨论了 Δp、ΔN取值的一种特殊情况,即 Δp=ΔN时,为使输出谐波最小,Δp、ΔN的最优取值为0.25。实际上,随着ΔP、ΔN取值的变化,上、下桥臂调制出的阶梯波的阶梯变化时刻将发生改变,从而使在交流侧得到的输出波形具有一定的差异。
表2为N为10的情况下,ΔP、ΔN取不同值时理论上交流侧输出的THD值。
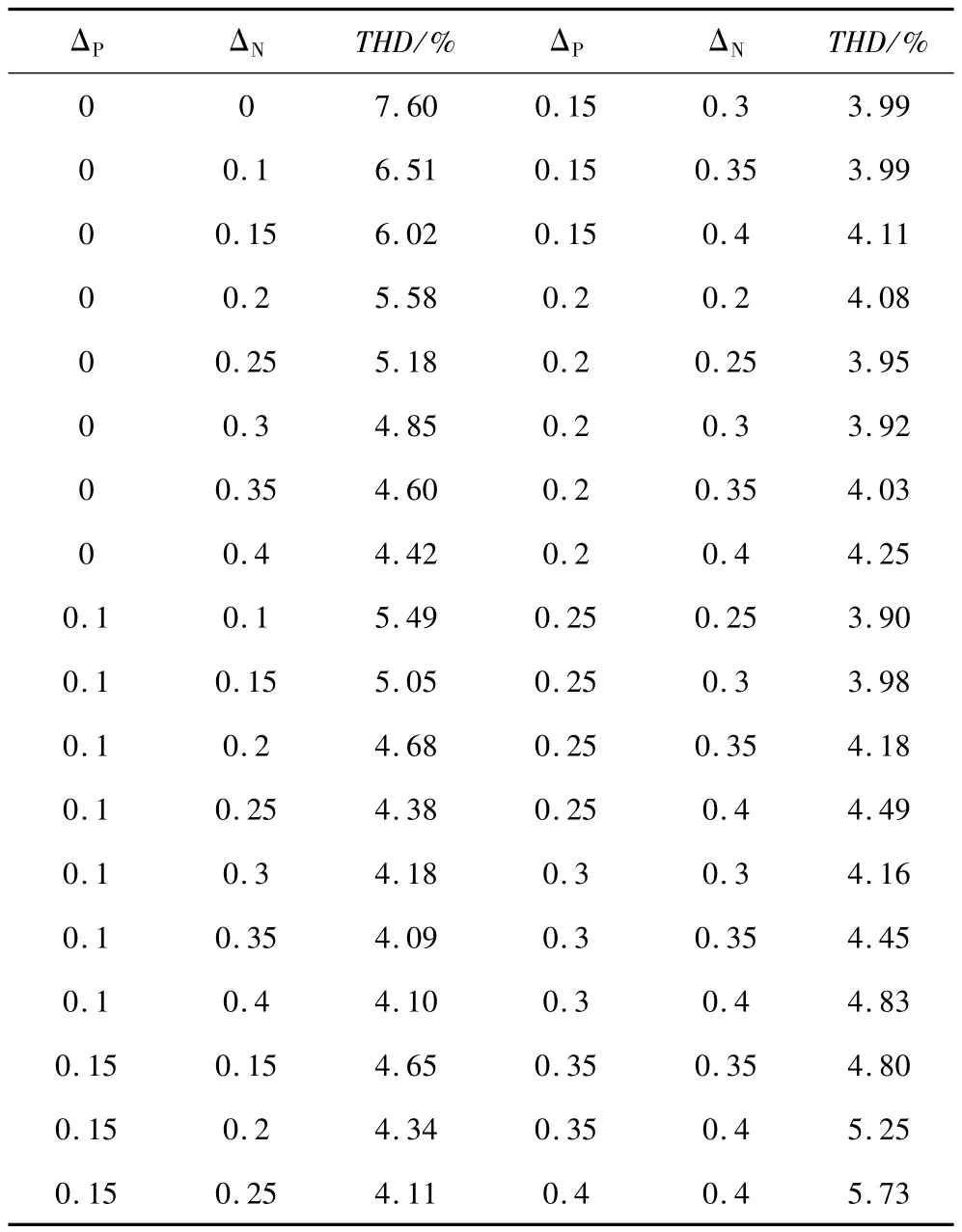
表2 ΔP、ΔN不同取值理论交流输出THDTab.2 THD theoretical value of AC output for differentΔP andΔN
根据表2可知,在固定的N值情况下(N取10),对于不同的ΔP、ΔN取值,调制得到的交流输出的近似效果呈现一定的规律。ΔP一定时,随着ΔN的增大,调制得到的逼近波形的THD呈现减小的趋势。当ΔP、ΔN其中有一个较接近0.25,另一个与0或0.5偏离较远时,逼近波形的THD越小。传统调制方法下交流输出波形的THD值最大,逼近的程效果最差,采用改进算法后,THD有不同程度的下降,部分取值组合情况THD甚至不足4%。
可以从一般情况来分析。设Δp=x,ΔN=y,且x,y∈0,0.()5。在任意相邻阶梯变化时刻t1、t2,有
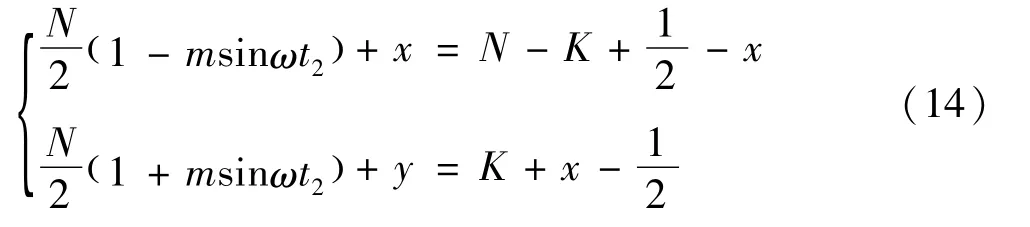
式中K为t1~t2时刻下桥臂投入的模块数。故输出波形参考值对应模块数为:
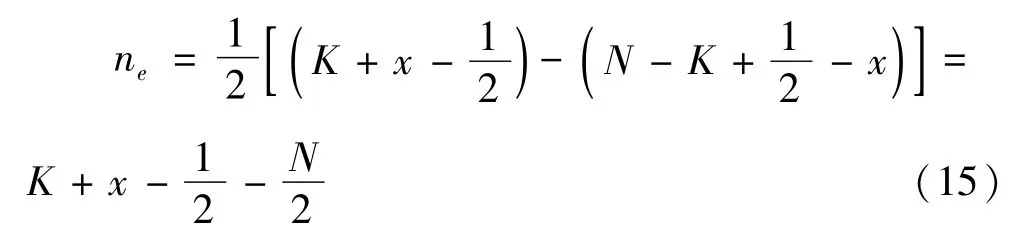
而在t+2及t-2瞬间分别有:

因此t+2及t-2瞬间输出对应模块数分别为:
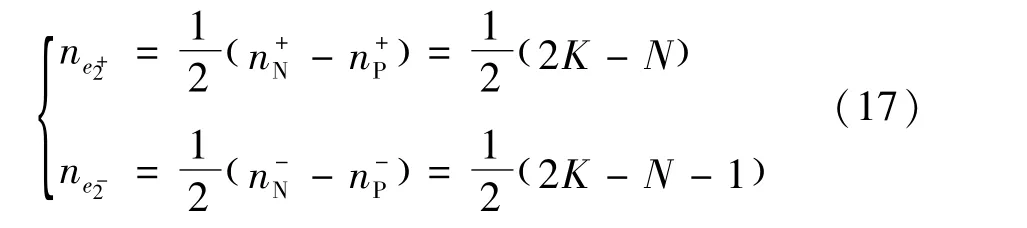
从而得到:
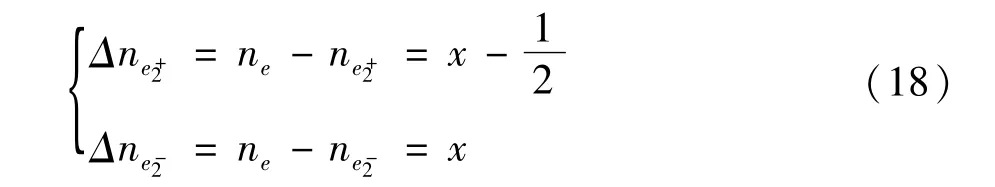
同理可得t1时刻最近电平逼近的正误差、负误差为:

为使输出波形逼近的效果尽可能最优,应使t1、t2时刻的正、负误差尽可能接近且较小,x、y的值应靠近0.25。表2中,当ΔP=0.2,ΔN=0.3时 THD值为3.92%,ΔP=ΔN=0.25时,谐波畸变率最低,为3.90%。显然,表2所得的结果与理论分析结果一致。
3 仿真研究
为进一步验证改进最近电平调制方法的效果,利用MATLAB/Simulink仿真环境建立三相每个桥臂10个SM串联的MMC逆变器模型进行仿真。直流输入电压、电容电压初始值分别为Udc=16.3 kV、Uc0=1 630 V,调制波频率为工频50 Hz,桥臂等效串联电阻为80Ω,桥臂串联电感及子模块电容分别为L=0.5 mH、C=10 mF,负载为阻感性且 Rz=12 kΩ,LZ=10 H,调制度m=1,各桥臂SM数目N取10。
仿真过程结合基于电容电压排序的电压平衡控制,检测各SM电容电压以及桥臂电流方向,在s函数的算法中完成对各SM电压由低到高排序,由桥臂电流方向判断充放电状态,根据各时刻要投入及切除的SM数目的多少,在充电和放电时,分别触发电容电压较低和较高的n个SM投入。仿真时调制发波实现过程的s函数输出逻辑如表3所示。实际上,各子模块电容电压并非保持在额定值Uc0,而是在额定值附近上下波动,为使每一时刻投入的SM数目指令值更准确,仿真过程中以各SM实际电压的平均值来取代传统NLM中的额定值,触发各SM的s函数实现流程如图7所示。

图7 子模块的触发s函数实现流程图Fig.7 Implementation flow chart of sub-module trigger s function

表3 发波实现过程的s函数输出逻辑Tab.3 Output logic of s function in the process ofwave generating
仿真中的直流侧电压恒定,验证改进型最近电平调制方法下,交流侧输出电压波形较传统最近电平调制,输出波形质量得到一定改善。
如图8为传统最近调制方法下MMC交流侧输出电压波形。输出相电压阶梯波为11电平,FFT分析其谐波畸变率为7.63%。采用改进型最近电平调制之后,部分ΔP、ΔN取值组合的仿真结果如图9~图10所示。ΔP=0.2,ΔN=0.3时相电压 THD值为3.92%,而 ΔP=ΔN=0.25时,相电压 THD值为3.89%。

图8 传统NLM三相交流输出波形Fig.8 AC outputwaveforms of traditional NLM

图9 ΔP=0.2,ΔN=0.3时MMC交流三相输出波形Fig.9 AC outputwaveforms of MMC inΔP=0.2,ΔN=0.3

图10 ΔP=ΔN=0.25时MMC三相交流输出波形Fig.10 AC outputwaveforms of MMC inΔP=ΔN=0.25
图8~图10为传统最近电平调制及ΔP、ΔN部分取值时交流侧的三相电压仿真波形。可以看出,与传统NLM调制相比,改进方法的输出的电平数增加一倍,电压电流波形明显变好。传统方法下交流相电压以及线电压的总谐波畸变率均超过7%,而两种ΔP、ΔN取值条件下,相电压总谐波畸变率在3.90%左右,线电压总谐波畸变率在3.45%左右,均较传统方法有明显下降。仿真过程中各子模块电容电压波形如图11所示,可以看出,由于加入电容电压平衡算法,各子模块电压基本稳定在1 630 V且变化趋势基本一致。
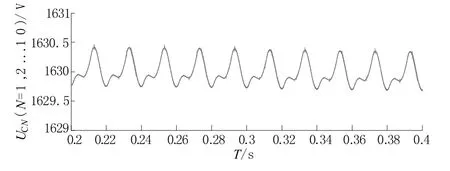
图11 子模块电容电压波形Fig.11 Capacitor voltage waveform of sub modules
4 结束语
最近电平调制方法在模块化多电平变流器中具有明显优势,且适用于模块数较多的应用情况。本文通过分析调制过程中阶梯波的形成过程,结合模块化多电平结构自身特点,通过改变近似函数来改变阶梯变化时刻的方式,分析比较了不同桥臂调制偏差值下MMC交流输出电压的效果,并进行在MATLAB/Simulink环境中进行了仿真。结果表明采用修正的NLM调制方法时,交流侧输出与传统方法相比有更好的谐波特性,仿真结果与理论分析结果相一致。
