考虑不确定性影响的微电网优化重构
2017-12-20张百甫周步祥邓苏娟魏金萧唐浩
张百甫,周步祥,邓苏娟,魏金萧,唐浩
(1.四川大学 电气信息学院,成都610065;2.四川电力设计咨询有限责任公司,成都610094)
0 引 言
近年来,化石燃料的环境污染受到人们的日益关注,而清洁、高效、灵活的分布式发电获得研究者的青睐。微电网重构是通过改变一些分段开关和联络开关的状态来改变网络的拓扑结构,但不改变系统的约束条件[1]。针对微电网重构问题,学者们提出了一些方法,文献[2]采用了层次分析法对微电网的脆弱性进行了评估,利用改进的蚁群算法对微电网重构进行寻优,仿真结果验证了所提方法的可行性;文献[3]采用加权熵理论对微电网的脆弱性进行了评估,并利用元细胞蝙蝠算法进行求解,仿真结果表明所提方法能及时为调度人员提供有效重构结果;文献[4]以微电网负荷损失最小为目标,采用邻接矩阵对微电网拓扑结构进行筛选,并利用粒子群算法对模型进行求解,仿真结果验证了所提方法的实用性;文献[5]以微电网数学模型和元件的可靠性参数为基础对微电网的脆弱性进行了评估,并利用搜索矢量拟态物理学算法进行了寻优,算例验证了所提模型的有效性和正确性。
从以上可以看出,目前针对微电网重构问题的研究主要集中在目标函数和算法方面,而考虑微电网不确定性因素的影响几乎没有,在实际过程中,由于微电网的高复杂性造成了诸多的不确定性问题参与其中。本文采用一种基于云模型的随机方法来捕获微电网中的不确定性因素影响,并以系统网损最小和供电质量最优为目标函数,通过改进的大爆炸算法进行求解。最后以33节点微电网标准模型作为案例研究,验证了所提方法的有效性。
1 微电网重构模型
1.1 目标函数
本文以微电网网损最小和供电质量最优为目标函数。
(1)系统网络损耗最小。以微电网有功损耗作为系统的网络损耗,即:
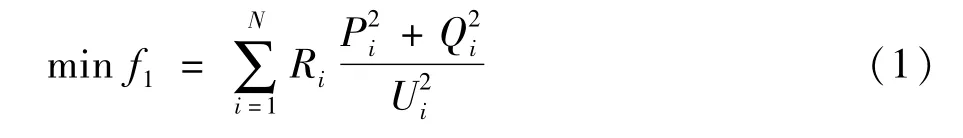
式中f1为微电网的网络损耗;N为微电网支路总数;Ri为第i条支路电阻;Pi、Qi、Ui分布为第i条支路的节点有功、无功功率及节点电压。
(2)电压偏差最小。电压偏差的大小反映出供电质量的高低,本文以节点电压和参考电压差的有效值作为电压偏差,即:

式中f2为电压偏差;U0为基准电压。
1.2 约束条件
(1)线路功率约束

式中 Pij,min、Pij,max分布为线路功率的上下限。
(2)线路电压约束
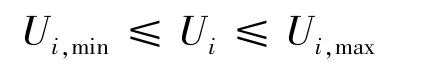
式中 Ui,min、Ui,max分别为节点 i的电压上下限。
(3)潮流方程
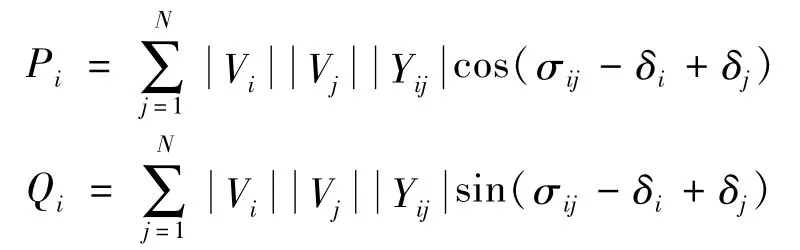
(4)线路电流约束

式中 Iij,min、Iij,max分别为支路 Lij的电流上下限。
(5)网络结构约束
优化重构后的微电网结构应为辐射状,即不是孤岛也不是环网运行。
1.3 多目标函数的处理
本文提出一种多目标规划方法,即利用模糊理论,将多个不同量纲的目标函数转化为同一量纲下的单目标函数,公式如下:
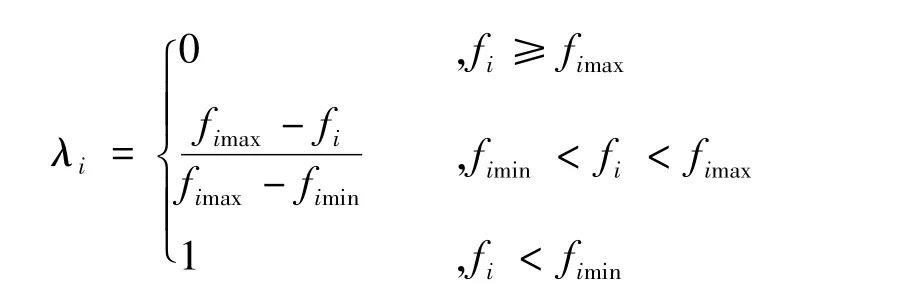
式中λi为fi的模糊隶属度值;fimax、fimin分别为目标函数fi的上下限。
由公式可以看出,当目标函数越小时,其模糊隶属度值越大,且隶属度值的计算具有独立性。利用模糊综合评价函数将各目标函数统一起来,组成了多目标函数的适应值,当目标函数不再扩展时,即可达到帕累托最优。本文利用综合适应度值来表征模糊满意度,公式如下:

式中γ为综合适应度值;n为总的模糊隶属度函数。最终得出以微电网负荷损失最小和供电质量最优为目标的单目标函数,即:

2 基于云理论的不确定性模型
云理论的概念最初由李德毅院士于1995年提出,用于处理定性概念与定量描述的不确定性模型[6]。云理论的提出为不确定性的描述提供了一种新的思路,有助于定性定量信息的相互转换。设U为一个定量论域,C为U上的定性概念,若x∈U,x为定量值,且x为C上的一次随机实现,则x对C的确定度μ(x)∈[0,1]是有稳定倾向的随机数:μ:U→[0,1],A x∈U,x→ μ(x),则其在论域 U上的分布称为云,每一个x称为云滴[7]。云模型用三个特征值表征:期望值Ex,熵En,超熵He。期望Ex是云模型的均值,期望En决定云模型的范围,熵He决定云滴谱,超过99.74%的云滴落在[Ex-3En,Ex+3En]范围内。超熵He有助于捕捉随机问题中不确定性的更多信息,它描述了云隶属函数的各种云滴;超熵He可以保留熵En在分布函数中的随机性;超熵He是熵的不确定性的度量,可以视为熵的熵。
正态云模型建立在正态分布函数和模糊集合隶属函数的基础上,正态云模型数学期望曲线方程式(4)所示,由此得出云滴。

逆向云发生器用于将不确定信息的定量数值转换成定性概念,计算公式如下:


3 模型求解
大爆炸算法(Big Bang-Big Crunch,BB-BC)由Erol和Eksin于2006年提出,它的灵感来自于宇宙的起源和演化[8],其主要优点是计算时间少,易于实现,收敛速度快,在一些实践中得到广泛的应用[9]。在大爆炸阶段,伴随着能量的耗散产生无序的随机粒子,而在大收缩阶段,随机分布的粒子变为有序。随机性是大爆炸阶段的关键特征,整个过程可看做是自然界的能量耗散最终由于受到引力的作用而收缩到一个局部或全局的最优点。由此原理,BB-BC优化算法主要包含两个步骤:大爆炸阶段和大收缩阶段[10]。在大收缩阶段,一些碎片解随机分布在搜索区域内,根据获得的各个目标函数值,计算每个碎片解的适应度值,所有碎片解集成为一个中心点即质心。质心主要依据式(9)产生:
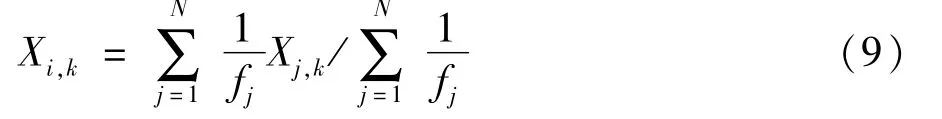
式中Xi,k为当前质心在n维空间中第k维的坐标分量;N为当前碎片解的总数;fj为第j个碎片解的适应度值;Xj,k为第j个碎片解在第k维的坐标分量。
下一次大爆炸新的碎片解通常分布在质心或最适应个体的周围,由此大爆炸和大收缩阶段将持续直到满足停止准则,围绕着质心新的碎片解公式为:

式中rj为用于改变碎片解的随机数,其服从标准正态分布;ω1为限制搜索空间大小的一个常数;Ximax、Ximin分别为第i个控制变量的上、下限。
受粒子群算法模拟飞鸟集群和鱼类群游的启发,群体的运动方向由个体和群体两方面经验决定,对于每一次迭代,粒子个体的运动方向由局部最优和全局最优计算而得。将这种方法引入BB-BC算法,不但利用质心而且利用了全局最优产生新的碎片解,改进的碎片解公式如下:

式中ω2、ω3均为控制参数,用于限制碎片解的搜索边界;Xl、Xg分别为局部最优和全局最优。
本文提出的基于云理论的微电网重构模型求解流程图如图1所示。

图1 基于云理论的微电网重构模型求解流程图Fig.1 Flow chart of solving reconfiguration of micro-grid model based on cloud theory
4 算例分析
本文以微电网标准的33节点为案例进行研究,系统结构图如图2所示,虚线为备用线路。设定基准电压为12.66 kV,初始损耗为226.6 kW,系统总负荷为5 084.26+j2 547.32 kVA,具体网络参数见文献[2]。

图2 33节点微电网模型Fig.2 33-busmicro-grid model
首先在确定性框架下利用改进的BB-BC算法得出网络损耗和电压偏差的优化结果,如表1所示。从表1可以看出,相比初始损耗,本文提出的重构方法效果显著,同时可以看出,改进的BB-BC算法提高了碎片解的收缩速度,在搜索能力方面有了较大的提高。

表1 确定性框架下网络损耗和电压偏差优化结果Tab.1 Optimization results of network loss and voltage deviation under the deterministic framework
考虑到分布式电源出力不确定性,其网络功率无法调度,本文将分布式电源视为PQ节点进行处理,负荷的不确定性也是影响微电网重构结果的一个因素,本文利用了随机框架模型,即利用第二节提出的云模型捕捉微电网中的不确定性信息。设定N=200为构建云模型的随机变量,随机框架下的优化结果如表2所示,表3列出了优化后的期望Ex,熵En,超熵He(注:表中电压偏差为标幺值)。由表2可以看出,考虑微电网中不确定性因素的影响,增加了重构结果的网损和电压偏差值,但这个结果更接近微电网运行的实际情况,对微电网的优化重构更具参考价值。基于云理论的随机框架下网络损耗和最低点电压偏差的二维云模型如图3所示,图3更形象地刻画出优化结果。

表2 确定性和随机框架下网络损耗和电压偏差优化结果的比较Tab.2 Optimal comparison of network loss and voltage deviation in both deterministic and stochastic frameworks
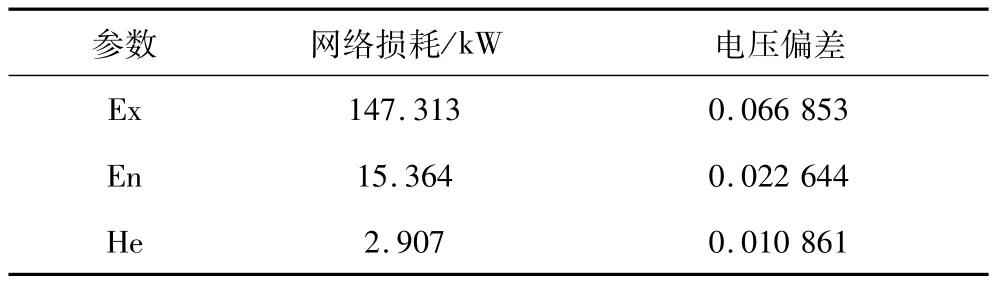
表3 基于云理论的随机框架下优化结果Tab.3 Optimal results of calculation based on cloud theory under the stochastic framework

图3 随机框架下网络损耗和最低点电压偏差的二维云模型Fig.3 Two-dimension cloud model of network loss and low voltage deviation under the stochastic framework
5 结束语
考虑到微电网中可再生能源出力和负荷不确定性的参透影响,本文提出了一种基于云理论的随机框架来处理微电网重构不确定性因素,同时引入一种改进的BB-BC算法对模型进行求解。仿真结果表明本文所提方法在处理微电网重构方面具有良好的效果,更符合工程应用实际情况,可提供更多关于不确定性参数的信息。此外,结果还表明,改进的BBBC算法在寻优能力方面有较大的提高。
