考虑电网脆弱性的输电网扩展规划模型
2017-12-20张弘历李华强王羽佳王炫丹
张弘历,李华强,王羽佳,王炫丹
(1.四川大学 电气信息学院,成都610065;2.成都供电公司,成都610000)
0 引 言
随着新能源和负荷的大规模接入,电力系统将面临着更多的不确定性。传统以经济性与安全性为主导的电网规划体系[1-4]已不能满足现在电网建设的需求,亟需补充和完善[5]。将电力系统脆弱性作为电网安全性与稳定性的延伸引入电网规划,将对规划建设坚强的电网将具有指导和借鉴意义[6]。
然而传统的电网脆弱性指:系统在遭受扰动或故障影响下,电网的电压水平和支路传输能力不断弱化的特性[7]。故传统的脆弱性研究大都从电网元件的角度出发,仅仅考虑电网单一元件的相对脆弱性[8-10],忽略了电网整体拓扑结构与全局运行状态脆弱性对电网经济与安全运行的影响,无法简单有效的衡量不同电网间的脆弱程度。因此,本文提出了电网全局结构与状态脆弱性的概念,并将其有效的运用到电网规划中去。
现有研究[11-14]分别指出电网网络拓扑与系统潮流负载率的非均匀性是电网趋于自组织临界状态的重要原因。当电网处于自组织临界状态时,任何微小的扰动都可能引发停电事故,甚至引发连锁故障,造成大面积停电[15]。因此在输电网规划伊始就考虑电网结构与状态的均匀性是必要,它可有效阻止电网进入自组织临界状态,降低系统脆弱程度,防患于未然[16]。
但电网实际运行状况表明,仅从电网网络拓扑与系统潮流负载率的均匀性角度来衡量电网的脆弱程度是不合理的,它忽略了电力系统网络拓扑结构脆弱度与支路潮流负载率大小对电网运行状态的影响。显然,高负载率下均匀的电网比低负载率下均匀的电网更脆弱。可见,国内外相关研究大都从仅从电网均匀性角度出发,且搭建的评估模型不够完整,尤其在电网规划方面未见有深入研究和应用。
本文首先基于传统电网脆弱性评估方法,结合电力系统均匀性理论与经济学中的基尼系数指标,提出了电网结构与状态全局脆弱因子模型对电网全局脆弱性进行评估。其次,在综合考虑电网经济性、电网结构全局脆弱因子、电网状态全局脆弱因子以及电网安全约束集的基础上构建了多目标电网规划模型。然后,在求解过程中,先针对各目标量纲不统一,权重不易获取问题,本文采用主成分分析法,对每代种群中个体进行综合评估,再采用改进混沌交叉变异遗传算法优化得到最优规划方案。最后,以Garver-6节点系统和Garver-18节点系统进行算理分析,证明了本文所提规划模型的合理性和有效性。
1 基尼系数模型
基尼系数是20世纪初意大利经济学家基尼根据劳伦兹曲线定义的来判断收入分配公平程度的指标[17]。如图 1所示。
实际劳伦兹曲线与绝对公平线所包围的面积为A,实际劳伦兹曲线与绝对不公平曲线所包围的面积为B。
定义基尼系数:

从基尼系数的定义可知,基尼系数可以有效的用一个数值从整体上反应某系统分布的均匀程度,简单直观。基尼系数越大代表该系统分布的均匀性较差;反之亦然。但基尼系数只能衡量系统内部的均匀程度,忽略了系统个体大小差异的属性。于是本文依据电力系统的网络拓扑结构与实际运行状态的属性差异,结合基尼系数指标构建了电网结构与状态全局脆弱因子模型用来衡量不同电网之间的脆弱性。
2 电网结构全局脆弱因子
2.1 电网节点电气介数模型
在现实中人们常常运用网络理论来简化描述复杂系统。文献[18]指出电力系统作为一种典型的非线性复杂系统,结合复杂网理论与电力系统特性可将其简化为一个有向加权网。其中,可以将节点按电网特性分为负荷、发电与联络节点3种。
传统复杂网络理论认为电网介数指标能有效地衡量网络拓扑中各节点在实际电网中的重要程度。但该指标是建立在假设潮流在两节点之间只通过最短路径传输的基础上,显然不符合电网实际运行状况。于是本文采用电气介数指标来衡量电网节点的重要度,具体模型见文献[7]。
2.2 全局结构脆弱因子
如本章前文所述,节点电气介数科学有效的量化了节点在电网网络拓扑中的重要度。节点电气介数分布的均匀程度能够有效的体现电网网络拓扑结构的均匀程度。故本文首先基于基尼系数理论,建立电网的节点电气介数基尼系数指标,以衡量电网网络拓扑结构均衡程度。但该基尼系数指标只能衡量节点重要度在电网中的分布情况,忽略了电网节点重要度大小不同的属性。有可能造成节点重要度主要集中在高重要度区域的电网与主要集中在低节点重要度区域的电网基尼系数相同,电网脆弱性也相同的现象,这不符合实际电网运行情况。
文献[19]指出节点度能够有效的衡量节点在电网网络拓扑中的重要度。基于此,本文运用加权平均节点度数对电气介数基尼系数进行修正得到电网结构全局脆弱因子。
定义如下:设节点度向量 D=(D1,D2,…Dn),则节点的加权平均节点度:
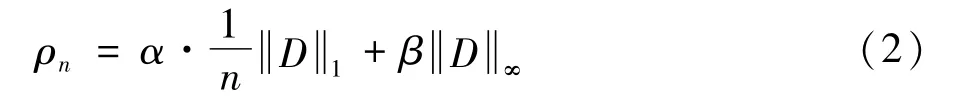
α,β为权重因子,且α+β=1;定义:

由定义可知α≤β,这样可以有效的突出最大节点度对电网全局结构脆弱性的影响,避兔了平均值可能出现的魅蔽现象。电网结构越均匀,各节点度越小,则加权平均节点度越小。
于是可以修正得到电网全局脆弱因子:

式中Gn为节点电气介数基尼系数。
综上,根据加权基尼系数定义的电网全局结构脆弱因子综合体现了系统节点重要度分布均匀程度与节点重要度大小对电网结构脆弱性的影响。模型更加科学有效。
2.3 全局状态脆弱因子
电网支路潮流负载率可以有效地衡量潮流对各支路的占用情况。支路潮流负载率的基尼系数能够有效的衡量系统运行状态的均匀性。设支路i的最大有功传输容量为Pimax,系统运行时支路i的实际潮流负荷为Pi,可得支路i的负载率为:
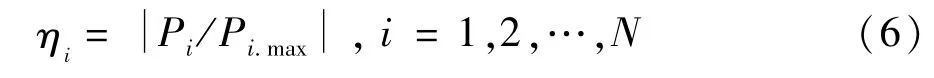
式中N为支路数。
建立电网各支路潮流负载率的基尼系数模型,求解电网状态分布基尼系数。由前文分析可知,支路潮流负载率基尼系数只能衡量负载率在系统中的分布状态,忽略了各电网支路潮流负载率大小不同的差异。有可能造成集中高负载率情况下的电网与集中低负载率情况下的电网基尼系数相同的,电网的脆弱性相同,这不符合电网的实际运行状况的。为了避兔该种不合理情况的出现,文献[20]运用平均负载率对其进行修正,但可能会出现指标相互魅蔽的现象。因此,本文类似于电网结构全局脆弱因子,本文采用加权平均负载率对负载率基尼系数进行修正得到电网状态全局脆弱因子。
设支路负载率向量 η=(η1,η2,…,ηN),则支路潮流的加权平均负载率ρf为:

于是可以得到电网状态全局脆弱因子为:

式中Gf代表电网支路潮流负载率基尼系数。
综上,根据加权基尼系数定义的电网全局状态脆弱因子综合体现了系统支路潮流负载率分布均匀程度与支路负载率大小对电网状态脆弱性的影响。模型更加科学有效。
3 电网规划模型
本文以新建线路为规划变量。在满足各新建线路的回数约束ωi、电网安全约束集Xp以及电网正常运行约束的前提下,综合考虑了电网的投资建设成本C、线路运行网损成本Ploss、电网全局结构脆弱因子Gl,O为违反安全约束惩罚量。电网的扩展规划模型如下:

其中,式(9)为目标函数向量;式(10)、式(11)为电网安全约束集。
相应的多目标函数如下:

其中式(12)为规划方案的扩建投资贾用(万元),k1为资金回收系数;k2为工程固定运行贾率;Ω1为新建线路集合;ci为单位长度线路造价,li为线路i的长度;xi为线路i新建回路数;式(13)为系统可变运行贾用(万元),即年网损贾用,k3为年网损贾用系数;Ω2为网络中已有线路和新建线路的集合;ri为线路i的电阻;Pi为正常运行方式下线路i输送的有功功率;式(14)为全局结构脆弱因子;式(15)为全局状态脆弱因子;式(16)为违反网络安全约束的惩罚项,Peni为第i种网络约束的惩罚系数;Hi为第i种网络约束的违反量。

式中r为贴现率;n为工程经济适用年限。

式中ρ为网损电价;τ为最大负荷损耗时间;U为系统的额定电压;
该模型约束条件计及系统正常运行和N-1检验下的各种约束以及各新建线路的整数型约束,具体如下:
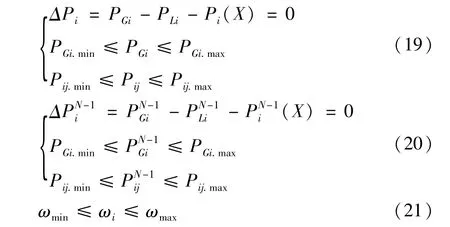
式(19)为N运行条件下,系统潮流约束方程、发电机出力约束、支路容量约束;式(20)为N-1运行条件下,系统潮流约束方程、发电机出力约束、支路容量约束;式(21)为支路回数约束。其中PGi.min为发电机i的容量下限;PGi.max为发电机i的容量上限;Pij.min为支路ij的潮流下限;Pij.max为支路ij的潮流上限;PGi为发电机正常运行时的容量;PN-1Gi为N-1运行状态下发电机的容量;ωmin为各新建支路回数的下限;ωmax为各新建支路回数的上限。其中功率单位为MW。
4 模型求解
电网规划作为多目标非线性优化问题,存在着量纲不统一,权重选择困难,各目标难以协调的问题,传统方法大都采用多目标权重法[21],模糊集分析法[22],分层优化[23]等依赖专家经验的评估方法,客观性较差,评估结果主要取决于专家的理论和经验水平。为了解决多目标规划权重不易选取的问题,本文采用主成分分析法对电网规划方案进行综合评估。主成分分析法是1901年Pearson对随机变量的综合评估而引入的,它以严格的数学理论为基础,能够根据数据的特性得到有效的评估结果,相比其他评估方法,该方法评价结果更为客观合理,比较符合实际情况[24]。
在优化算法上本文采用改进的遗传算法,与传统遗传算法结构所不同的是:本文将混沌系统随机性的特点运用到遗传算法的交叉与变异过程中,改进效果十分明显。具体如下,首先本文将变异从交叉操作中分离出来,使其成为独立的并列于交叉的寻优操作。在进行交叉操作时,以‘门当户对’的原则进行个体配对,利用混沌序列确定交叉点,实行强度最弱的单点交叉,以确保算法收敛精度,削弱和避兔寻优抖动问题;在变异操作中,利用混沌序列对染色体中的多个基因进行变异操作,以避兔算法早熟。流程图如图2所示。

图2 改进遗传算法流程图Fig.2 Improved Genetic algorithm flowchart
5 算例分析
本文以Garver-6节点系统为算例进行仿真计算,认为六个节点之间都可以相互连接。优化结果接线图如图3所示。其中细线为所添加的线路。
仿真参数:功率基准值为100 MVA,电压基准值为220 kV,工程使用年限n=15a,单位长度建设投资贾用cj=80万元 /km,贴现率r=10%,工程固定运行贾用k2=5%,年运行小时数τ=3 000 h,单位电价ρ=0.3元 /kW·h。
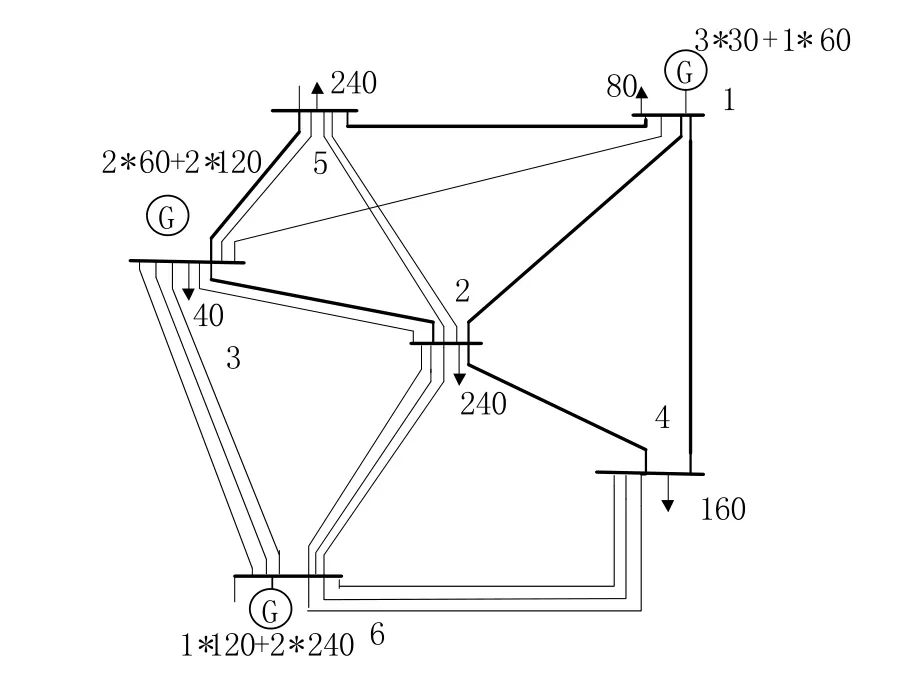
图3 规划线路图Fig.3 Planning routemap
仿真得到该规划方案的节点电气介数分布基尼系数与支路潮流负载率的劳伦兹曲线如图4、图5所示。

图4 节点电气介数劳伦兹曲线Fig.4 Lorenz curve of node electrical betweenness

图5 支路负载率劳伦兹曲线Fig.5 Lorenz curve of branch load rate
根据式(4)、式(7)计算得到节点平均度数为3.7,最大节点度数为5,支路平均潮流负载率为0.567,最大支路潮流负载率为0.711,电网结构全局脆弱因子和电网状态全局脆弱因子如表1所示。
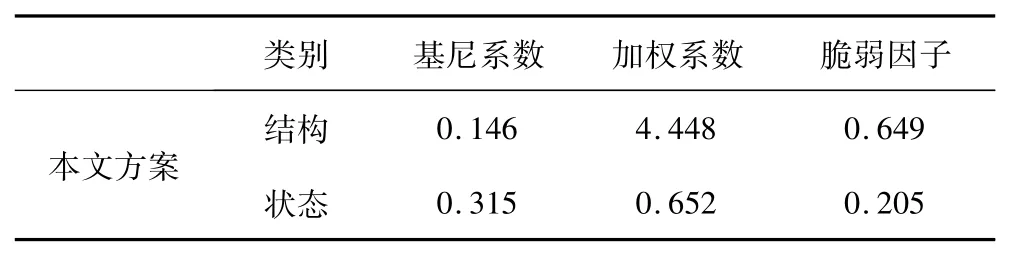
表1 全局脆弱因子Tab.1 Global vulnerability factor
从图4、图5可以看出,本文所提电网规划模型的节点电气介数与支路潮流负载率的劳伦兹曲线都逼近绝对公平线。根据前文分析的结论可以简单而又直观的得到电网的网络拓扑结构与运行状态分布较为均匀,但无法有效的说明电网的脆弱程度。通过节点的度和负载率的修正得到了电网的结构与状态全局脆弱因子如上表1所示,该指标既能有效的衡量电网整体的均匀程度,又能科学的反应电网内部各指标的差异性。
为了验证本文所建立模型的有效性准确性和可行性,本文采用其他电网规划模型进行对比仿真,仿真结果如表2、表3所示。方案一为本文所采用的规划模型,方案二为文献[6]考虑电网脆弱性的电网规划模型。两种方案均满足N-1安全准则。

表2 全局脆弱因子对比Tab.2 Comparison of global vulnerability factor
从表2、表3可以看出,首先,方案一的电网建设贾用为7 109.795万元,比方案二电网建设贾略大。这主要因为方案一综合考虑到电网结构与状态均匀性以及降低重载线路潮流负载率,需要多架设支路来分担重载线路的潮流同时使电网拓扑结构更加合理,进而降低规划模型的脆弱性,增强电网抵抗各种不确定性风险的能力,仿真结果也证明了这一点;其次,由于方案一规划模型网络结构拓扑与支路潮流分布的合理性,所以网损贾用也明显低于另两种方案。综合以上的分析,本文所建立的规划模型以牺牲一部分建造成本为代价来达成整体目标的最优,兼顾运行的经济性和系统的均匀性与脆弱性,这样的电网更为经济可靠。
同样,对Garver-18节点的系统的仿真计算也证明了本文规划模型的可行性。Garver-18节点系统是按静态安全的N准则里研究输电规划的常用算例。优化结果的网络连接图如图6所示。其中虚线部分为新添加的线路。

表3 Garver-6节点系统优化仿真结果对比Tab.3 Optimization simulation results comparison of Garver-6 node system

图6 Garver-18连接图Fig.6 Garver-18 connection diagram
各目标参数如表4所示,其中方案一为本文规划模型,方案二为文献[25]给出的仿真模型。
从表4可知,两种方法都满足正常运行状态与N-1状态下的安全可靠性准则,但本项目所采用的规划模型建设贾用更低,且电网结构的支路与节点全局结构脆弱因子更小,电网的网络拓扑结构与运行状态更加均匀合理,所以电网结构更加坚强可靠,运行状态更加经济合理。由此也验证了本文所建立模型的可行性。

表4 Garver-18仿真结果Tab.4 Garver-18 simulation results
6 结束语
本文提出了一个较为完善的多目标电网规划数学模型。首先从电网拓扑结构与运行状态的均匀性出发,结合基尼系数理论构建了电网全局脆弱因子模型,能够有效地衡量电网的结构与状态全局脆弱性。其次,运用主成分分析法对规划方案的经济性、安全约束集与电网全局脆弱性进行综合评估,得到电网规划模型的综合评估指标。最后采用改进混沌交叉变异遗传算法对所选取的方案进行优化,得到最优方案。仿真结果证明了本文所提模型的可行性与有效性。同时,本文所提规划模型能够很好的解决电网规划约束条件和目标函数不易处理的问题,符合实际工程需要。
