基于模糊聚类与随机森林的短期负荷预测*
2017-12-20黄青平李玉娇刘松刘鹏
黄青平,李玉娇,刘松,刘鹏
(华北电力大学电气与电子工程学院,北京102206)
0 引 言
电力系统短期负荷预测是电力部门非常重要的工作之一,它影响整个系统的调度、发电和电能存储的方案制定和实施。长期以来如何提高负荷预测的精度是国内外学者一直致力研究的目标,负荷预测精度会直接影响电网运行的资金和安全[1-2],因此提出可行性好、精度较高的负荷预测方法具有非常重要的意义。
目前,负荷预测方法主要划分成两种:传统方法和智能预测方法[3]。传统预测方法主要有时间序列法[4]、回归方法[5]和指数平滑法[6]。时间序列法对不定性的因素如温度、湿度考虑不充分,当天气发生骤变时,预测误差较大。线性回归方法形式简单但处理非线性能力差,预测精度低。指数平滑法基于“近大远小”理论,采用历史负荷进行加权平均,即越近的负荷加权系数越大,但该方法仍然不能反映日期、气象等因素与负荷的非线性关系。近年来,基于智能原理的负荷预测方法得到了广泛应用[7-10],特别是神经网络和支持向量机。神经网络克服了传统方法不能自主学习以及影响因素考虑不全面等问题,但缺点也较明显:容易陷入局部最优,隐藏层单元数目难以确定等。SVM预测方法很好的保证全局最优,但其核函数确定困难且模型构建存在较多的人为因素,不利于预测精度的提高。
RF是数据挖掘中重要的分类回归算法,由多棵决策树组合成分类器,具有泛化能力强、所需调节参数少和预测精度高等优点,被应用于多个领域[11]。但RF回归算法应用于负荷预测的文献较少[12-13],且传统负荷预测方法以及智能预测方法(ANN和SVM)自身的局限性大,已经不能满足预测精度的需求。于是本文考虑将RF回归方法应用于短期负荷预测,并结合模糊聚类技术,提出一种模糊聚类与随机森林结合的负荷预测方法。该方法首先依据模糊聚类原理分析,根据样本相似性选取训练样本;然后利用随机森林算法建立预测模型;最后应用真实的负荷数据验证该方法的有效性。
1 C均值模糊聚类算法
1973年,Bezdek将早期的模糊聚类进行推广,提出了C均值模糊聚类[14],它是利用隶属度来确定每一个样本数据属于某一类的聚类算法。鉴于电力负荷具有周期性变化特性,选择气象、日期等负荷影响因子作为聚类的状态特征变量,与待预测日影响因子相似性高的同类特征数据作为随机森林训练样本的输入,保证了数据的统一性和相似性。
设 A={A1,A2,…,An}为预测日的样本集合,每个样本xi有m个特征属性,那么预测样本xi可表示xi={xi1,xi2,…,xim}T,(i=1,2,…,n),C均值模糊聚类是将数据集A划分为c类,得到c个子集A1,A2,…,Ac满足:
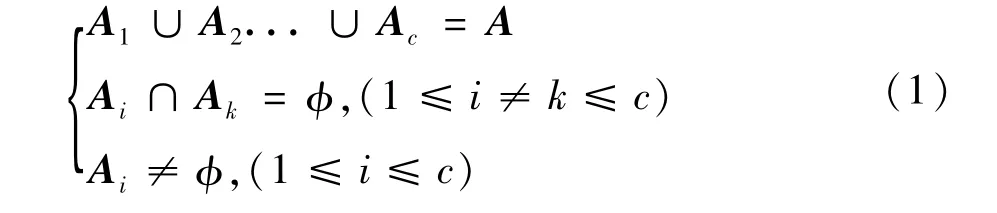
数据样本 xi属于 Ak(1≤k≤c)的隶属度为 Uki,满足:

则有目标函数成立:

式中dki是第i个样本到第k类的中心距离;ck是第k类的聚类中心。
C均值模糊聚类算法的目的是要取目标函数的最小值,目标函数最小的两个必要约束条件为:

式中m为隶属度的加权系数。
该算法的基本流程为:
(1)给定两个基本的参数m和c,一般m取2,计算出初始聚类中心;
(2)初始化隶属矩阵U;
(4)设置隶属度最小变化量ε,迭代终止条件,否则l=l+1并跳回步骤3执行。
首先将样本进行分类,设待预测样本xb={xb1,xb2,…,xbm}T,然后计算待预测点与各样本类别的隶属度函数,将最大隶属度所对应的类别作为待预测点所属类别,最后利用类别对应的样本作为随机森林的训练样本进行负荷预测。
2 随机森林的基本理论
随机森林算法是美国科学家LeoBreiman结合bagging集成学习和随机属性子空间理论提出的有监督学习算法[15]。该算法通过bootsrap重抽样方法对原始样本进行抽样,每个抽样样本的容量与原始样本一样;每个bootsrap抽样的样本进行CART(分类回归)决策树建模;最后组合的多棵CART决策树作为随机森林,森林中每棵决策树投票结果则是最终的预测结果。
2.1 CART决策树
20世纪70年代后期和20世纪80年代初期,Quinlan提出了ID3决策树算法[16],后期将ID3决策树算法改进提出C4.5决策树算法;1984年,Breiman等多位统计学家提出了CART决策树算法,CART是一种二分递归分割技术,每个非叶结点被划分为两个叶子节点。这三种算法都是采用自顶向下的贪心方法构造决策树,不同的是属性选择度量。每棵决策树在生长过程中,需要选择某个属性作为分裂节点,选择最优的属性进行分裂的依据是属性选择度量,决定了节点属性分裂情况。其中ID3决策树算法使用信息增益作为属性选择度量,C4.5决策树算法选用增益率作为属性选择度量,CART决策树算法利用基尼指数作为属性选择度量,CART决策树算法利用基尼指数作为分类树的属性选择度量;最小二乘偏差作为回归树的属性度量。
(1)CART分类树的度量属性
设数据集D中有n个不同的类别Ci,Ci,D是数据集D中Ci类元组的集合,和和分别是D和Ci,D元组的个数,则CART决策树使用基尼指数Gini(D)计算公式为:
式中 Pi为 Ci类元组出现的频率,用进行估计。
基尼指数需要考虑每个属性的二元划分,若属性A是离散值,A的二元划分将D划分为D1和D2,则在给定划分的条件下,D的基尼指数为:

属性A的二元划分导致的不纯度降低为:

考虑每个属性可能的二元划分情况,选择该属性产生最大化不纯度降低(具有最小基尼指数)的子集作为它的分裂子集。即属性A的ΔGiniA(D)越大,GiniA(D)越小,在A上的分裂效果越好。
(2)CART回归树的度量属性
分裂节点利用最小二乘偏差作为衡量回归树的最优分裂属性。利用最小二乘偏差计算节点的属性的划分公式为:
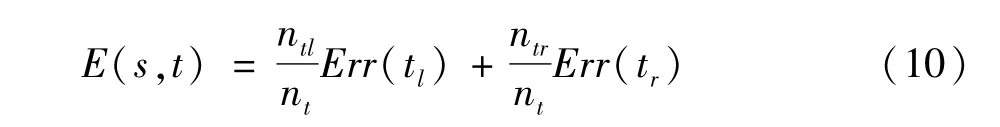
式中t是节点;s为属性值;nt是节点个数。Errt(t)为节点的误差其计算公式为:

划分的标准是E(s,t)越大,分裂效果越好。
2.2 集成学习
集成学习是将多棵CART决策树组合在一起,每棵决策树对分类或回归的结果进行投票,决定最后的预测结果。由于单一CART决策树回归的精度不高,容易出现过拟合、陷入局部最优等问题。为克服单一CART决策树的缺点,Breiman在随机森林中引入Bagging算法,该算法依据统计学中Bootstrap思想,从原始样本中可放回重复抽样获取等规模的训练样本,并将生成的CART决策树组合进行集成学习,提高了分类器的泛化能力[17]。假设N是原始数据集D的样本容量,那么D中每个样本没有被抽到的概率为1/(1-1/N)N,且当 N趋于 ∞ 时,1/(1-1/N)N收敛于1/e≈0.368。该结果表明原始数据集D中大约有37%的样本不被抽到,这些未被抽中的Bootstrap数据称为袋外(OOB)数据。Breiman证明了利用随机特征构建决策树和OOB估计泛化误差,有利于提高预测的精度[18]。此外Bagging算法可以同时进行多棵决策树训练,减少了计算的时间,也是该算法的优势
2.3 随机森林算法
随机森林是{H(X,θi),i=1,2,...,k}k个决策树集成学习的组合分类器,针对回归问题,取H(X,θk)的预测平均值作为最后的预测结果。
设 D={(xi,yj)i=1,2,...,N;j=1,2,...,m}为训练数据集,其中x是数据集D的一个训练样本,y为样本的特征变量,原始训练数据集有N个记录,M个特征变量,算法过程见图1。

图1 随机森林算法的结构图Fig.1 Structure diagram of random forest algorithm
该算法的基本流程为:
(1)从数据集D中,boostrap抽样得到与原始数据集容量一样的K个数据集,构建K个训练子集。每个数据集包括N个样本和m个特征变量,即从N个记录boostrap抽样抽取N个记录,从原始数据集的M个特征变量中抽取得到m个特征变量,反复抽样k次,形成训练样本集Dtrain。

(2)根据CART决策树算法,构建随机森林里的决策树。这些决策树利用CART决策树算法进行训练,决策树在生长过程中,随机从M个特征变量中选择m个特征变量,利用最小二偏差法计算出最优的特征变量作为分裂节点。进行决策树训练之后,利用袋外(OOB)数据作测试集 S={S1,S2,...,Sk},有利于提高预测精度。
(3)假设每棵决策树预测的输出为 {Y1,Y2,...,Yk},随机森林最后的预测结果为所有决策树预测的平均值,即:

3 模糊聚类结合随机森林的短期负荷预测理论分析
3.1 预测输入变量
由于影响负荷预测的因素众多,为了提高负荷预测的准确度,考虑将日气象因素和实时气象因素以及历史负荷结合建立预测模型,本文选择的输入预测样本参量,如表1所示。
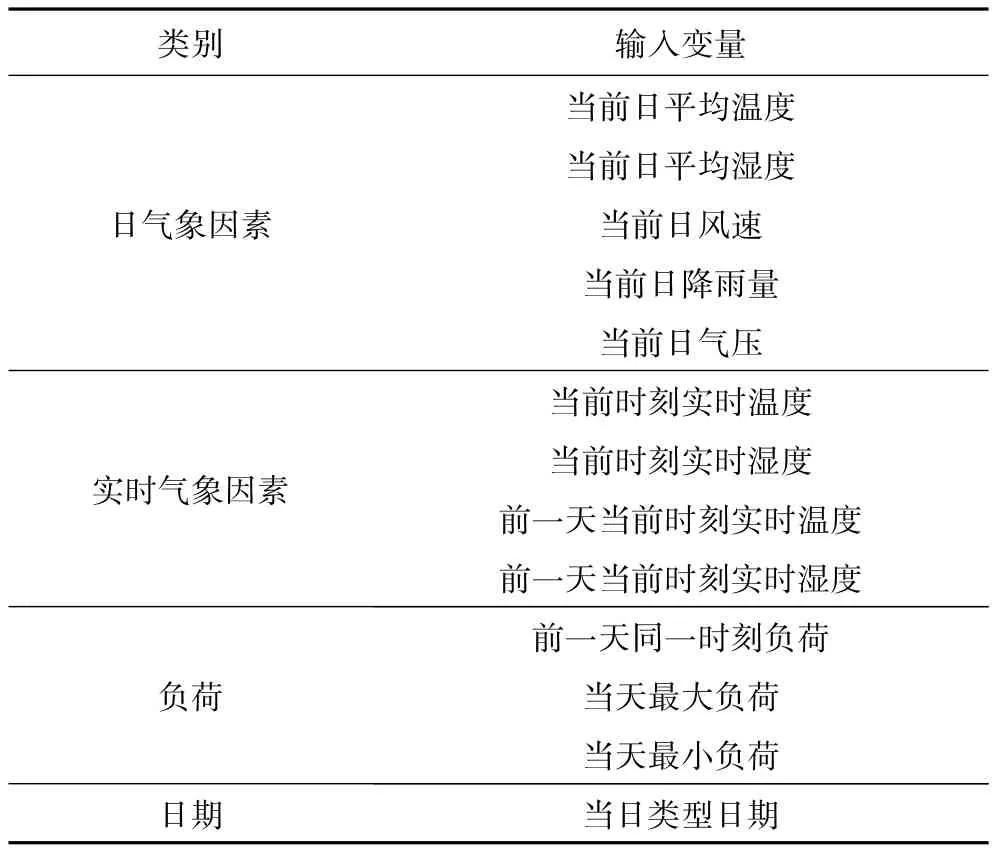
表1 输入变量Tab.1 Input variables
3.2 数据的处理
由于输入输出数据单位不一致,在进行模型训练前,应对输入、输出的气象数据和负荷数据进行归一化处理,取值范围限定在[0,1]或[-1,1]之间,归一化公式为:

式中xmax和xmin代表的是数据集的最大和最小值。
3.3 负荷预测流程
模糊聚类和随机森林进行短期负荷预测时,利用模糊聚类算法将预测样本分类后,找到待预测点所对应的类别,所属类别对应的样本作为随机森林预测模型的输入样本,得到最终的预测结果,如图2所示。
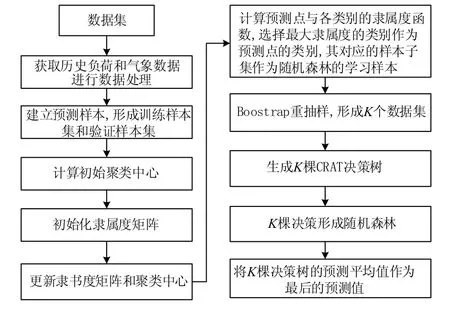
图2 负荷预测流程图Fig.2 Flow chart of load forecasting
4 应用实例及结果分析
本文结合安徽某地区历史负荷数据和气象数据对该地区2009年4月29日全天24小时的负荷进行预测,并将模糊聚类和随机森林结合(IRF)的预测结果与传统的SVM算法和BP神经网络所得预测结果进行比较,如表2所示。表2的时间是从0∶01∶00-0∶24∶00。

表2 三种方法的预测结果对比Tab.2 Comparison of the prediction results of the threemethods
画出2009年4月29日3种方法预测的负荷曲线对比图,见图3。
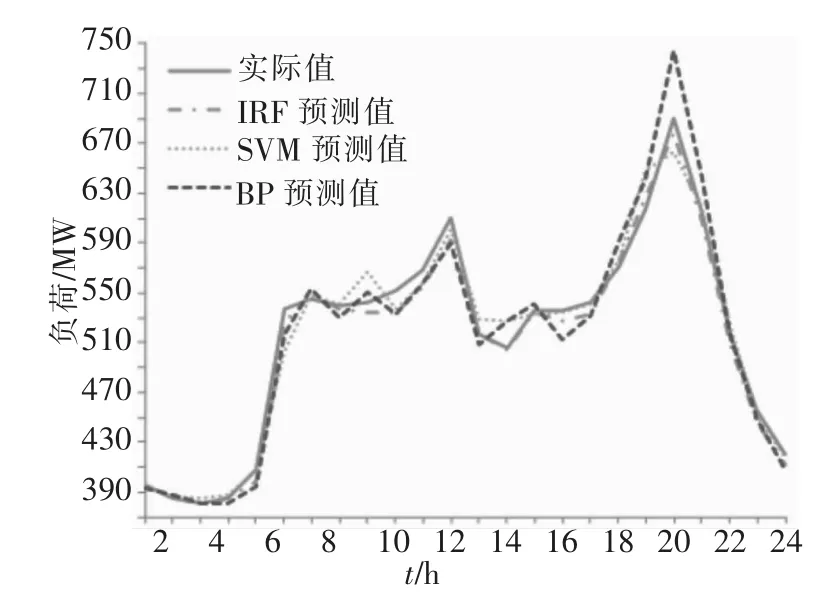
图3 2009年4月29日3种方法预测的负荷曲线Fig.3 Comparison of threemethod of forecasting load curves on 29,April 2009
与其它两种方法的结果比较,本文方法得出的负荷预测曲线更接近实际负荷曲线,为清楚观察对比结果,分别计算24小时平均相对误差和平均绝对百分比误差(MAPE)得到表2,MAPE计算公式为:

由表2得知,模糊聚类和随机森林结合进行负荷预测结果优于传统的SVM算法和BP神经网络方法预测结果,为了进一步证明所提算法的有效性,本文对2009年4月28~5月4日连续工作日的24小时的负荷进行预测,其中5月1日~5月3日为节假日,结果见表3。

表3 4月28日~5月4日三种方法的预测精度对比Tab.3 Comparison of the prediction accuracy from April 28 to May 4 results about threemethods
由表3可知,本文所提出方法的负荷预预测精度高于传统的SVM方法预测精度,且5月1日~5月3日为节假日的预测误差明显小于SVM的预测误差,体现了该方法较好的鲁棒性。
5 结束语
本文提出模糊聚类与随机森林相结合的方法进行负荷预测,该方法利用随机森林算法的泛化能力高、鲁棒性好的优势,同时结合模糊聚类算法选取相似度高的输入样本作为随机森林预测模型的训练样本,不仅保证输入特征量的一致性而且简化了训练模型。实例表明,与传统的SVM和BP神经网络方法相比,该方法并有效地提高了短期负荷预测的精度,为电力需求侧负荷管理提供了一定的参考依据。
