果园货运链索横向振动非线性控制

李 君，薛坤鹏，杨 洲※，洪添胜



果园货运链索横向振动非线性控制

李 君1,2，薛坤鹏3，杨 洲1,2※，洪添胜1,2

（1. 华南农业大学工程学院，广州 510642；2. 华南农业大学南方农业机械与装备关键技术教育部重点实验室，广州 510642；3. 广东省现代农业装备研究所，广州 510630）

为有效抑制果园货运链索行进过程中的横向振动，提出采用一种非线性边界控制方法进行链索横向减振主动控制。考虑到多边形效应对链索振动造成的影响，基于Hamilton原理建立了复杂工况下轴向行进链索和边界作动器的动力学耦合模型。通过构建广义能量函数作为系统的Lyapunov函数，设计了受控链索的控制规律，进行了链索横向振动闭环系统的渐近稳定性证明推导。仿真与试验结果表明，通过作动器引入控制力，链索横向振动在主动控制率的作用下能够在5个周期内被有效抑制。该文为货运行进链索的振动控制研究提供了理论参考。

农业机械；运输；振动；山地果园；链索；作动器；李雅普诺夫方法；振动控制

0 引 言

货运链索系统在复杂地形条件下铺设灵活，能够满足山地丘陵果园货物运输的需求[1]。在受迫振动和参数振动的影响下，货运链索在工作过程中处于非稳态并产生横向周期性激振，托索机构冲击、时变索力以及风雨荷载等不确定因素促使链索的激振运动更趋复杂[2]。链索横向振动如不加以抑制，将对货运系统的运行安全性和可靠性带来不利的影响。研究有效的减振方法来减小复杂工况下的货运链索运动失稳现象发生，对于提高工作过程中的安全可靠性具有重要的研究意义。

如忽略抗弯刚度，货运链索可模型化为轴向行进弦线，即沿轴线方向平移、受较大轴向力作用而张紧的弦线[3]。提高轴向运动弦线稳定性的早期振动控制方式主要是采用无源元件进行阻尼和刚度的被动式调节，随着主动减振技术的发展，以线性模型为理论基础的时域或频域的分析方法应用广泛[4-6]。Foda[7]考虑了运行速度、端部支座和阻尼的变化，通过作动器引入适当控制力，并运用格林函数来抑制轴向运动弦线的横向振动。Tan等[8]探讨了具有一般边界的线性轴向运动弦的主动波控制方法，采用行波消去法建立了双控制力的主动控制率，结果表明运动弦线的振动可被有效抑制。理论研究证明非线性系统的控制可通过线性或者非线性控制规律来实现，因此以滑模变结构控制和Lyapunov稳定性理论为代表的非线性控制方法在轴向运动弦线控制领域开始引起关注[9-11]。Li等[12]通过讨论轴向运动的非线性弦在下游或上游边界控制时的振动抑制问题，证明利用Lyapunov方法可在边界上采用线性负速度反馈达到指数稳定。为减小行进弦线张力、激励、负载等不确定参数变化对系统稳定性的影响，相关研究结果表明采用自适应控制方法来修正控制模型以适应弦线和扰动的动特性变化是可行的[13-15]。鲁棒控制、神经网络以及模糊控制等方法在轴向运动弦线研究中均能获得满意的振动抑制效果和稳定性[16-18]。

货运链索由相邻的水平和垂直链环交错连接，和弦线在几何构型上存在差异。链索经过托索装置时产生多边形效应的振动激励，对货运系统的工作稳定性会产生不可忽视的影响。国内外有关行进弦线类横向振动及其抑制的研究大多都是对运动弦线、行进梁和滚子输送链抽象问题进行分析，未见轴向运动链环系统减振控制有关的研究报道。为有效抑制果园货运链索行进过程中的横向振动，需要在分析系统动力学特性的基础上，设计有效的边界作动器进行主动减振。因此，本文基于Hamilton原理建立复杂工况下行进链索和边界作动器的动力学耦合模型，利用Lyapunov方法进行链索横向振动闭环系统的渐近稳定性研究，从而抑制多边形效应作用下运动链索横向振动，以期为果园货运链索的振动控制与稳定性分析提供依据。

1 数学模型的建立

假设货运链索的各个支撑装置高度和间距相同，忽略链环之间的黏性阻尼和弯曲刚度，假设链索行进时只有竖直方向的振动，边界条件和外部扰动为零，从而可以将其理想化为具有均匀分布集中载荷的轴向运动弦线模型[19]，其单个跨度内模型如图1a所示。

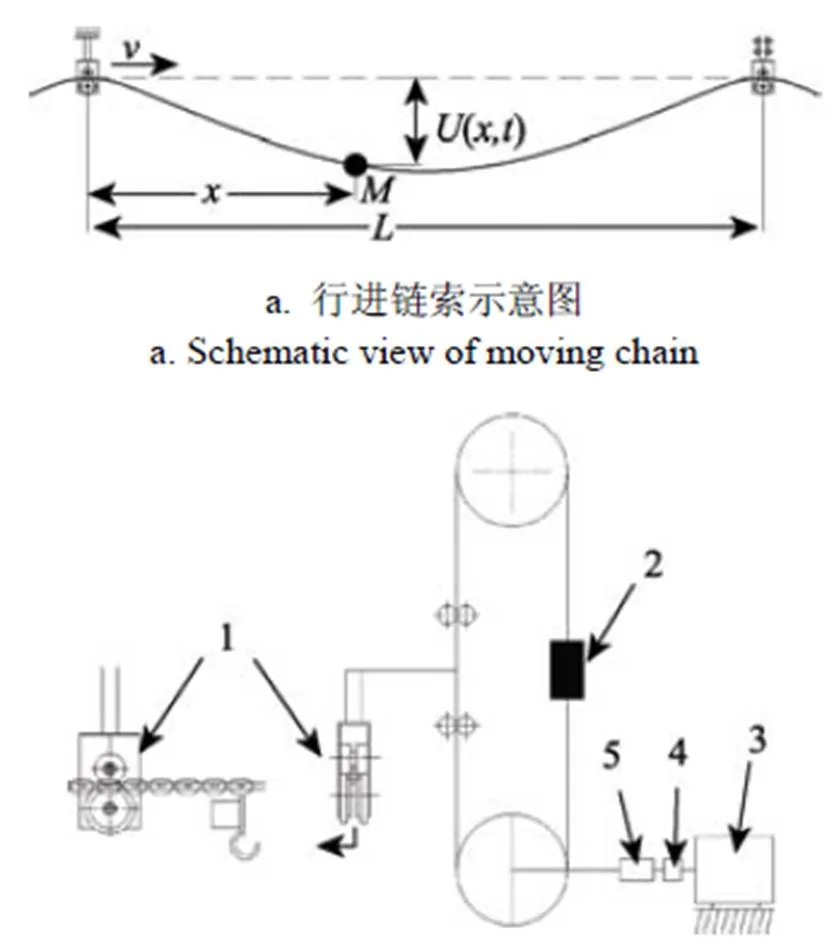
1. 作动器 2. 平衡块 3. 步进电动机 4. 磁粉离合器 5. 扭矩传感器

1. Actuator 2. Counterbalance 3. Stepper motor 4. Magnetic powder clutch 5. Torque sensor

注：为集中质量，kg；为集中质量与左托索轮的距离，m；为时间，s；(,)为链索横向振动位移，m；为链索行进速度，m·s–1；为单跨跨度，m。

Note:represents the lumped mass, kg;is the distance between the lumped mass and left supporing wheel, m;is time, s;(,) is the transverse vibration of chain, m;is the travel speed of moving chain, m/s;is the length of a single span, m.

图1 行进链索系统

Fig.1 Moving chain system

假设链索的轴向运行速度恒定不变，左端支撑装置的托索轮固定，右端支撑装置的活动托索轮作为作动器的末端执行器，为行进链索提供控制力F，通过作动器与链索的耦合进而达到抑制该跨度内行进链索横向振动的目的，如图1b所示。(,)是链索的横向振动位移，其中为时间，为集中质量与左托索轮的距离。相关偏微分算式的简化形式见式（1）：

链索在位置竖直方向的振动速度为：

根据虚功原理，可得作动器左侧受控链索的动能1、势能1以及作动器装置的动能2为：

式中δ为微小增量符号；为链索张力，N；是磁粉离合器、扭矩传感器的转动惯量之和，kg·m²；1、2分别为托索装置、平衡块的质量，kg；为作动器输出同步带轮直径，m；U(,)是同步带轮线速度，m/s；为当量线密度，kg/m，其表达式为：

式中0为链索线密度，kg/m；为单跨跨度，m；k为第个集中质量，kg；(–x)为狄克拉函数；x表示第个集中质量与左托索轮的距离，m；为集中载荷的数量。

作动器非保守力F()的虚功方程：

考虑到作动器右侧的货运链索振动为外部扰动，因此构建作动器的动力学方程需要导入右侧链索的能量方程，可得作动器右侧链索的动能3和势能2：

根据Hamilton原理[20-22]，推导可得：

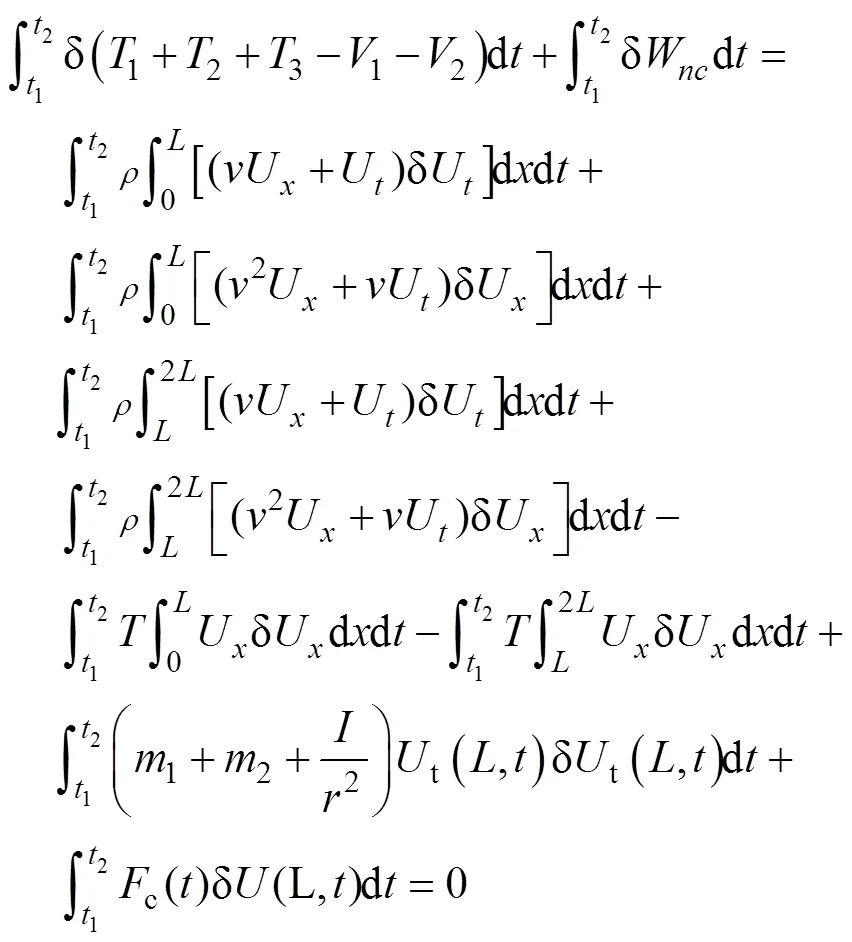
对式（8）进行分部积分，并代入边界条件(0,)=0和(2,)=0，化简可得：

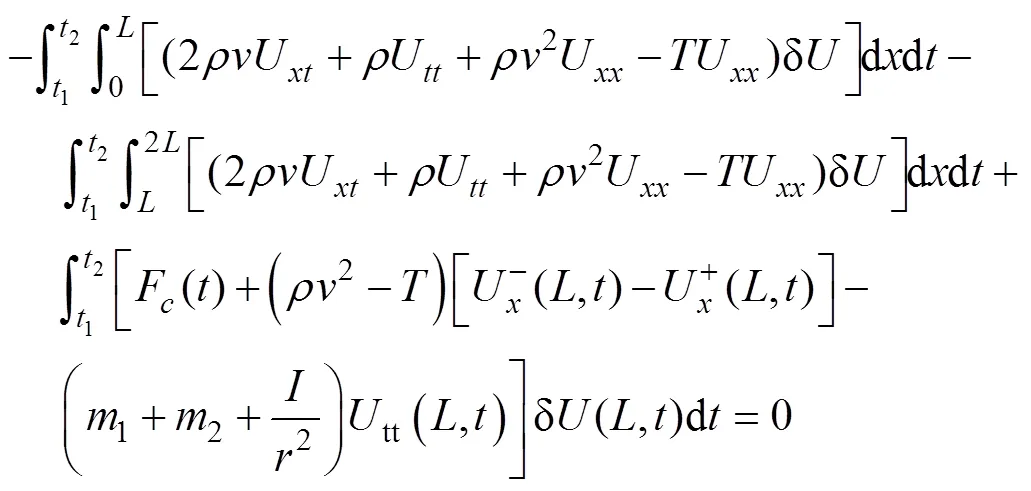
整理得货运链索和作动器的动力学微分方程：

链索的初始条件为：

式中为单跨链索最大垂度，m。

2 Lyapunov函数构建

如图1a所示，左托索装置为受控跨度内货运链索的左侧约束点，作动器动力学方程为受控链索的右边界条件，并且边界激励引起的振幅远小于跨度。

Lyapunov法是通过构建广义能量函数来分析控制系统稳定性的一种方法[23-25]。为简化计算，构建货运链索Lyapunov函数时，右边界的多边形效应看成作用在边界位置的一个外部扰动力()，即

作动器未进行振动控制时，链索的机械能为

为分析未控链索横向振动有界性，选取Lyapunov函数0为：

式中均为正常数。

利用平方和不等式，得：

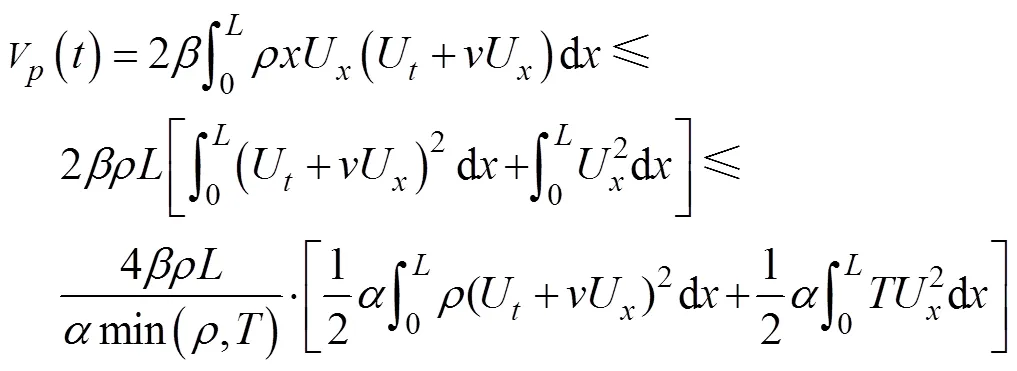
选取恰当的，可满足0≤1≤1条件，即

由式（13）~（16）可得：

可知，工作过程中未受控制货运链索的振动机械能是正定有界的。

定义辅助量k用于引入作动器的能量方程：

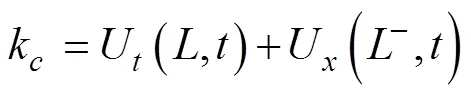
利用式（12）、（17）和（18），构建受控链索的Lyapunov函数为：

3 控制规律设计

作动器的控制力设计为：

其中：

式中是一个正常数。

将式（21）代入到式（20），得

令正常数满足如下不等式

将2代入式（23），结合不等式（24）可得：

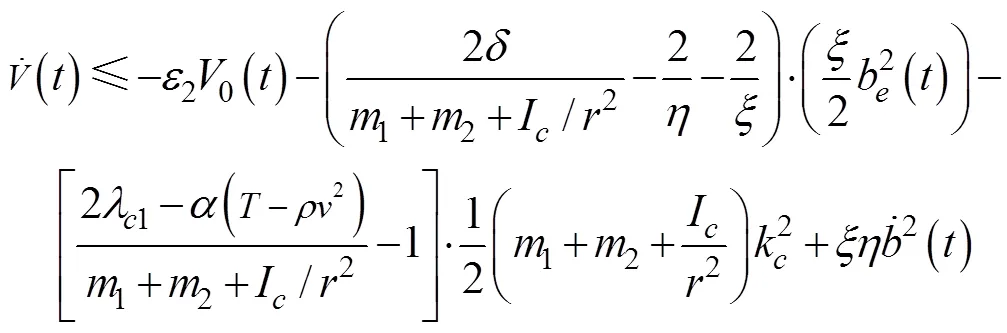
式中是一个正常数，若令：

由于托索位置多边形效应引起的边界激励是有界的，那么必定存在一个非负的正常数C使得：

将式（27）和式（28）代入到式（23）积分可得：

结合式（13）、式（17）、式（19）和式（29），可得：

由式（30）可知，货运链索的总机械能在作动器控制力的作用下渐进收敛到一个常数，因为多边形效应引起的边界激励比较小，并且和3均为比较小的正常数，可以认定ξηC/3是一个非常小的常数，最终货运链索按指数渐进稳定到安全的工作状态。

多边形效应引起的边界干扰通常为正弦形式的边界激励，即：

式中为链节的长度，m；为幅值，m；为相位角，rad。

类似推导可得：

进而可知：

因此，在多边形效应已知的条件下，同样可以构建相应的作动器控制力方程，使得货运链索的总机械能在作动器控制力的作用下具有指数渐进稳定性，进而保持链索稳定在安全的工作状态。

4 数值仿真分析

为验证链索横向振动非线性控制方法的有效性，采用数值仿真的方式进行计算求解。仿真模型参数来自国家柑橘产业技术体系果园生产机械化研究室安装在华南农业大学工程学院的货运链索试验系统。其中=6 m，=0.02 m，=0.2 m，0，ρ=0.79 kg/m，=8 kg，=1，=400 N，122.5 kg，I=1.1×10–7kg·m2，P=30 mm，0.55 m/s，0.05 m。根据式（17）、式（30）、式（31）以及式（33），可求得=0.25=0.01、λ1=80、λ2=30=0.08=0.083=0.0203。

采用数值计算方法进行链索横向振动控制仿真，货运行进链索在不受边界振动控制器作用下，在受控链索跨度中点的振动位移如图2a所示。

由图2a可知多边形效应增加了链索横向振动的不确定性，并且随着时间的增加链索其受影响振动会加剧。若多边形效应当成未知边界干扰和已知边界干扰进行处理，通过主动边界控制力作用，受控链索跨度中点处的振动位移分别如图2b和图2c所示。

图2 测量点振动位移仿真结果

由图2可知，货运链索在边界振动控制器的作用下，受控链索段的横向振动约在4.5个周期后收敛到稳定状态。虽然在边界干扰未知时，其振动幅度并没有衰减到零，但其振动幅度已能确保货运链索系统的平稳和安全运行，说明采用Lyapunov方法设计的控制律是有效的。

5 试验验证

由式（21）可知，通过对作动器作用点的位置及其前后的位置进行空间和时间微分，得到U(,)、U(L,)、U(,)和U(,)，进而可计算得到需要作用于作动器控制力的大小。按照控制规律的实施要求，本文设计了一种链索边界作动器振动控制系统，其试验装置主要由驱动机构、竖直位置调节机构及电控单元组成[26-28]，见图3a。

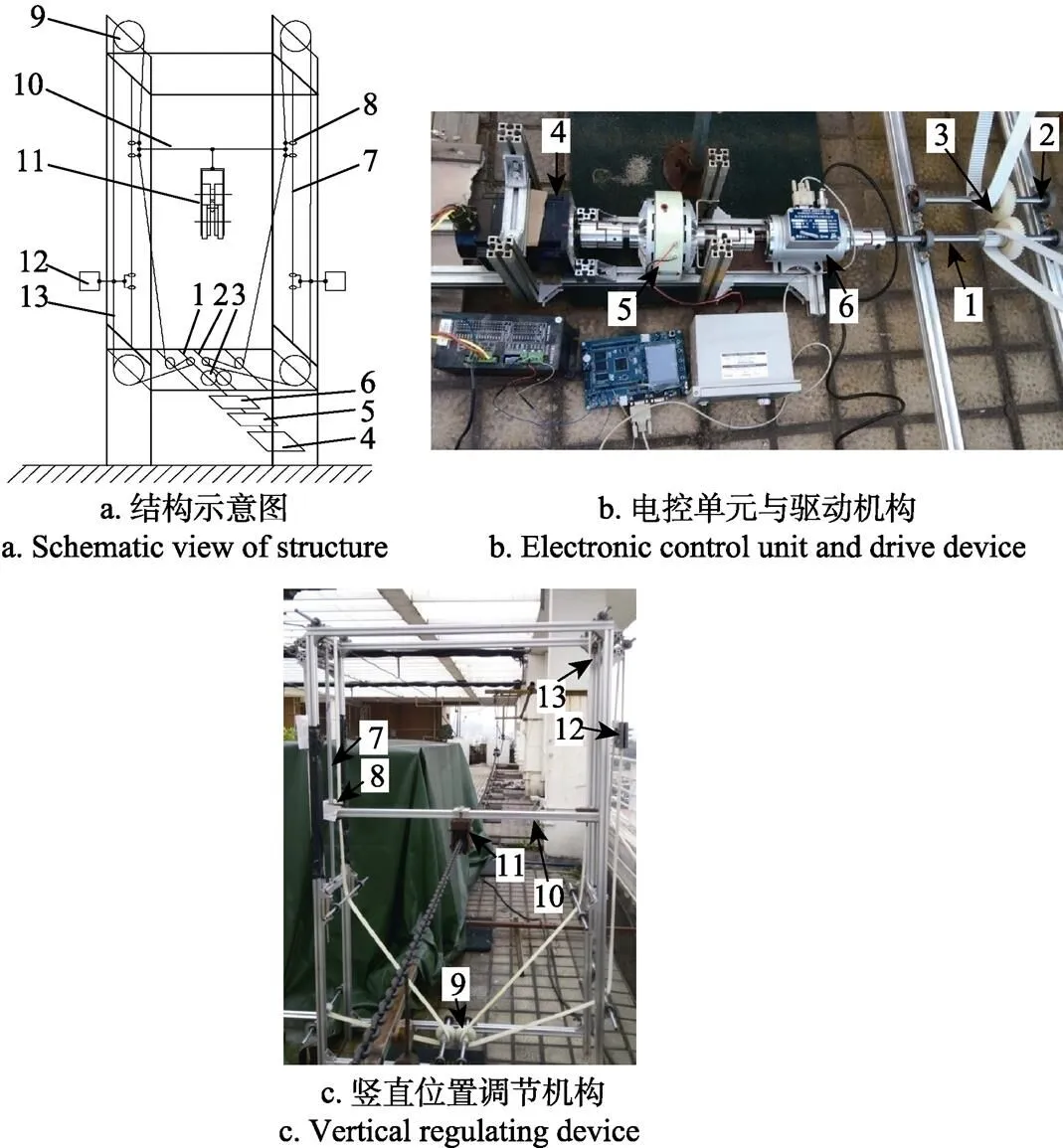
1. 动力输入轴 2. 从动轴 3. 主从动齿轮组 4. 步进电动机 5. 磁粉离合器6. 扭矩传感器 7. 滑动光杆 8. 箱式滑动轴承 9. 同步带轮 10. 横杆11. 托索装置 12. 平衡块 13. 同步带

如图3b所示，驱动机构由步进电动机、磁粉离合器和扭矩传感器组成，按照控制要求向竖直调节机构输出给定扭矩。步进电动机负责动力输出，可控制其转速和转向；磁粉离合器通过控制其输入电压大小改变其输出扭矩的大小；WDH-Z扭矩传感器监测其输出的扭矩、转速和转向。电控单元由图像采集装置、振动控制器、步进电机驱动器、磁粉离合器驱动器组成。电控单元根据图像采集装置反馈的链索振动加速度、速度和位置信号，结合货运链索的动力学模型，计算出减振装置当前需要输出的控制力的大小和方向，并将其转换成控制信号发送给步进电机驱动器和磁粉离合器驱动器，通过扭矩传感器检测驱动机构是否输出了目标扭矩。

如图3c所示，竖直位置调节机构由动力输入轴、从动轴、主从动齿轮组、同步带及同步带轮、滑动光杆及箱式滑动轴承组成，其功能是将驱动机构输送的扭矩转换成托索装置对货运链索的控制力。动力输入轴同轴安装主动齿轮与同步带轮，从动轴同轴安装从动齿轮与同步带轮。驱动机构输出的扭矩经动力输入轴，通过主从动齿轮对带动从动轴反向运转，进而使两侧的同步带产生运动，带动箱式直线轴承沿与其配合的滑动光杆上下平移，与此同时带动托索装置一起沿竖直方向运动，从而实现扭矩与控制力的转化。同步带内侧与承载托索装置的横杆连接，外侧均安装平衡托索装置质量用的平衡块，以减轻驱动机构的负荷。

系统控制流程如图4所示。

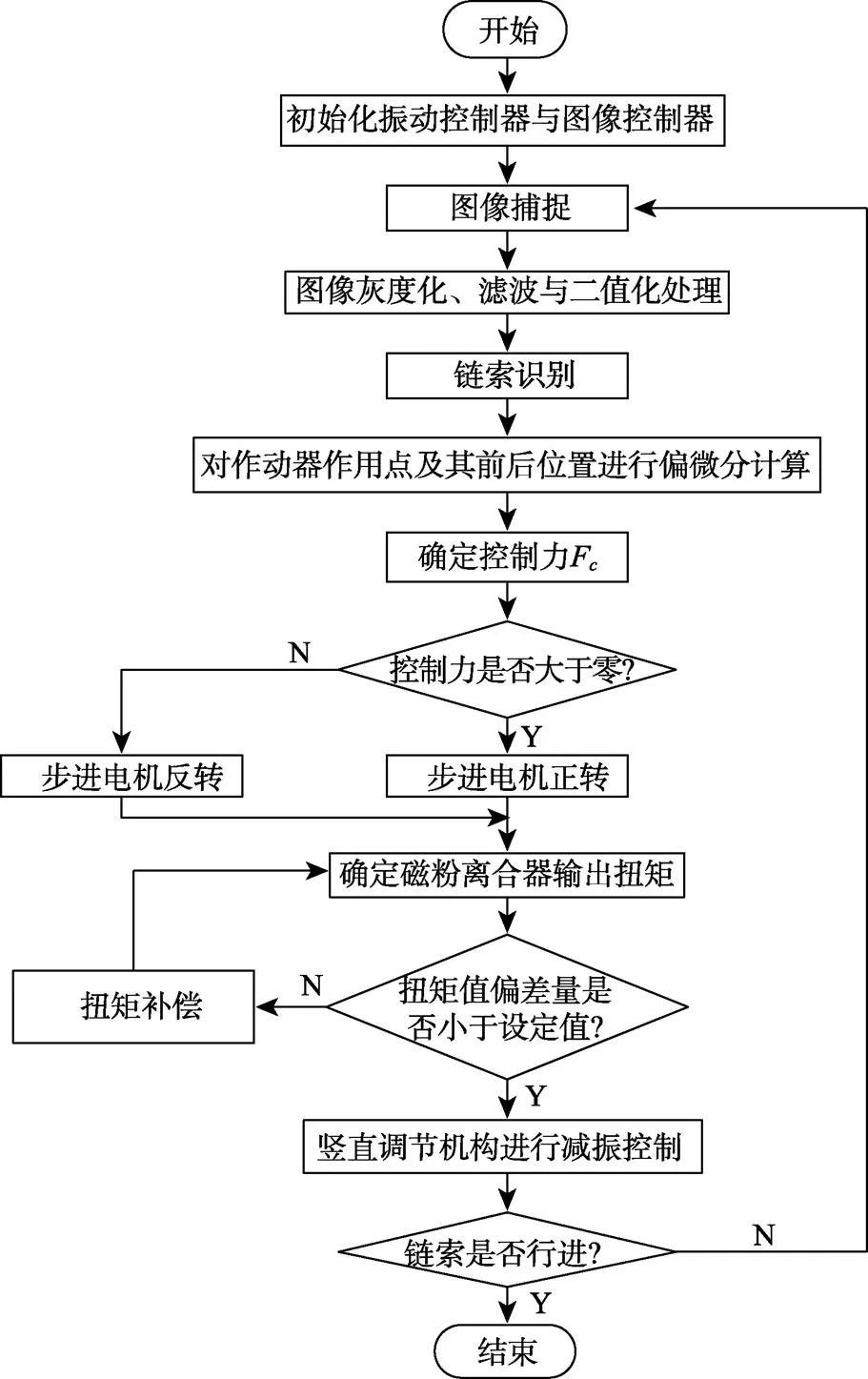
图4 控制流程图

如图5所示，振动控制器基于STM32F103开发板制作，图像采集装置由2个Z30A工业相机（数据采集速度150帧/秒，图像分辨率640×480像素）和Cortex-A9图像处理器组成。工业相机采集链索在水平和竖直方向上的实际位置图像，通过USB接口输入到Cortex-A9微处理器硬件平台的iTOP-4412开发板嵌入式四核处理器Exynos4412中进行处理[29]。将工业相机采集到的每一帧彩色图像转化为灰度图像，并进行混合滤波计算和自适应阈值二值化，获取行进链索的像素偏移量后，对比计算得到链索的实时位置信息。图像处理器再对链索观测点的位置进行数值微分，经RS232串口将计算结果发送给振动控制器。

图5 图像采集装置

试验验证的参数取值与数值仿真试验相同。如图6所示，在空载运行条件下，受控链索跨度中点的横向振动在边界控制器的作用下历时约5个周期后渐近稳定，说明施加主动的边界控制力可以得到较好的链索振动抑制效果。由于设计控制规律的过程中忽略了一些不确定因素，并且对货运链索的动力学模型进行了简化，因此系统的实际控制效果与仿真控制相比存在一定的偏差。

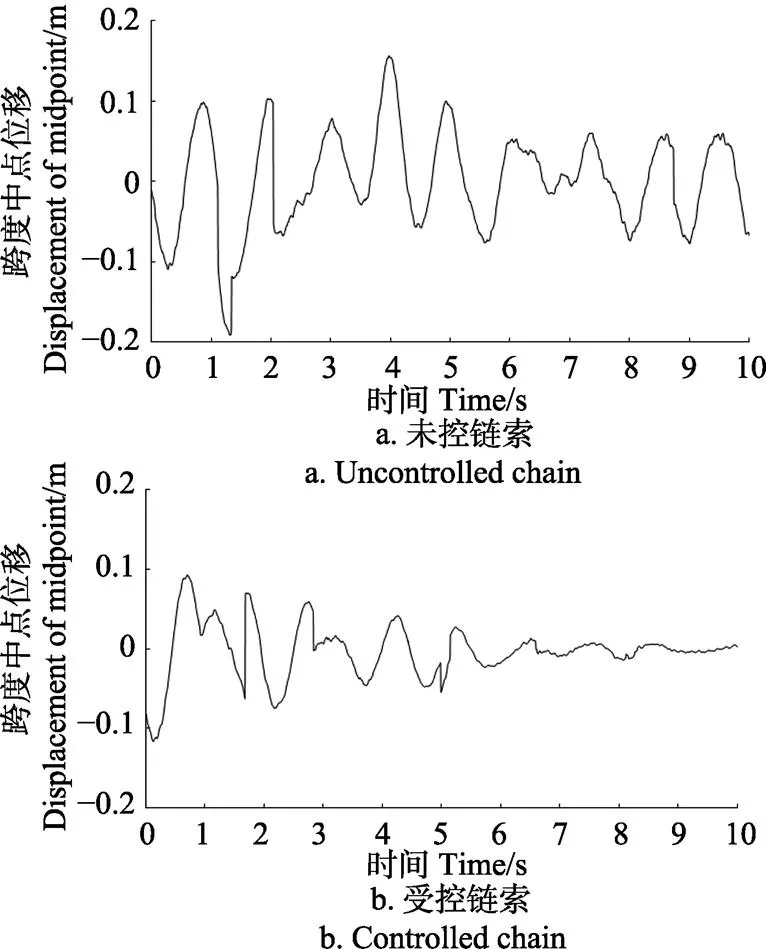
图6 测量点振动位移试验结果

6 结 论

1）考虑到多边形效应对货运链索横向振动的影响，基于Hamilton原理构建了复杂工况下行进链索和边界作动器的动力学耦合模型。根据广义能量函数进行Lyapunov函数的选取与控制率的设计，推导证明了链索横向振动能量在给定控制力的作用下能够达到指数稳定。

2）设计了一种链索边界作动器振动控制系统，链索振动位移采用图像采集方式处理。仿真和试验研究的结果表明：多边形效应增加了链索横向振动的不确定性，通过施加主动的边界控制力，链索横向振动能够在5个周期内快速衰减，从而可确保货运系统处于安全稳定的运行状态。

货运链索在工作过程中，承载量、链速、索力等参数的时变量很难准确检测，风雨激励等外界干扰也存在一定的不确定性，因此如何采用自适应控制方法对行进链索进行有效减振控制，本课题组将作进一步的探讨和研究。

[1] 洪添胜，苏建，朱余清，等. 山地橘园链式循环货运索道设计[J]. 农业机械学报，2011，42(6)：108－111. Hong Tiansheng, Su Jian, Zhu Yuqing, et al. Circular chain ropeway for cargo transportation in mountain citrus orchard[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(6): 108－111. (in Chinese with English abstract)

[2] 李君，薛坤鹏，杨洲，等. 果园货运链索风致振动非线性动力学分析[J]. 农业工程学报，2017，33(5)：75－81. Li Jun, Xue Kunpeng, Yang Zhou, et al. Nonlinear dynamics analysis for wind-induced vibration of orchard chain ropeway system[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(5): 75－81. (in Chinese with English abstract)

[3] 李君，李雪平，杨洲，等. 果园链索系统横向运动共振条件及频率分析(英文)[J]. 农业工程学报，2014，30(23)：50－57. Li Jun, Li Xueping, Yang Zhou, et al. Transversal vibration analysis of resonance condition and frequency for orchard chain ropeway system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014,30(23): 50－57. (in English with Chinese abstract)

[4] Alsahlani A, Mukherjee R. Vibration control of a string using a scabbard-like actuator. Journal of Sound & Vibration[J], 2011, 330(12): 2721－2732.

[5] Shahruz S M, Parasurama S A. Suppression of vibration in the axially moving Kirchhoff string by boundary control[J]. Journal of Sound and Vibration, 1998, 214(3): 567－575.

[6] Zhang W, Chen L Q. Vibration control of an axially moving string system: wave cancellation method[J]. Applied Mathematics & Computation, 2006, 175(1): 851－863.

[7] Foda M A. Vibration control and suppression of an axially moving string[J]. Journal of Vibration & Control, 2012, 18(1): 58－75.

[8] Tan C A, Ying S. Active wave control of the axially moving string: Theory and experiment[J]. Journal of Sound and Vibration, 2000, 236(5): 861－880.

[9] Shahruz S M, Kurmaji D A. Vibration suppression of a non-linear axially moving string by boundary control[J]. Journal of Sound and Vibration, 1997, 201(1): 145－152.

[10] 余小刚，张伟. 轴向运动弦线横向振动的变结构控制[J]. 福州大学学报(自然科学版)，2012，40(2)：217－221. Yu Xiaogang, Zhang Wei. Transverse vibration control of an axially moving string system by variable structure control[J]. Journal of Fuzhou University (Natural Science Edition), 2012, 40(2): 217－221. (in Chinese with English abstract)

[11] Kim D, Kim S, Jung I H. Stabilization for the Kirchhoff type equation from an axially moving heterogeneous string modeling with boundary feedback control[J]. Nonlinear Analysis Theory Methods & Applications, 2012, 74 (10): 3598－3617.

[12] Li T C, Hou Z C, Li J F. Stabilization analysis of a generalized nonlinear axially moving string by boundary velocity feedback[J]. Automatica, 2008, 44(2): 498－503.

[13] Nguyen Q C, Hong K S. Asymptotic stabilization of a nonlinear axially moving string by adaptive boundary control[J]. Journal of Sound & Vibration, 2010, 329(22): 4588－4603.

[14] Chen L Q, Zhang W. Adaptive vibration reduction of an axially moving string via a tensioner[J]. International Journal of Mechanical Sciences, 2006, 48(12): 1409－1415.

[15] 张伟，陈立群. 轴向运动弦线横向振动控制的自适应方法[J]. 机械工程学报，2006，42(4)：96－100. Zhang Wei, Chen Liqun. Transverse vibration control of an axially moving string system by adaptive method[J]. Chinese

Journal of Mechanical Engineering, 2006, 42(4): 96－100. (in Chinese with English abstract)

[16] Yang K J, Hong K S, Matsuno F. Robust adaptive boundary control of an axially moving string under a spatiotemporally varying tension[J]. Journal of Sound & Vibration, 2004, 273(4): 1007－1029.

[17] Huang J S, Chao P C, Fung R F, et al. Parametric control of an axially moving string via fuzzy sliding-mode and fuzzy neural network methods[J]. Journal of Sound & Vibration, 2003, 264(1): 177－201.

[18] Chao P C, Lai C. Boundary control of an axially moving string via fuzzy sliding-mode control and fuzzy neural network methods[J]. Journal of Sound & Vibration, 2003, 262(1): 795－813.

[19] Yang Z, Li X P, Li J, et al. Transversal vibration of chain ropeway system having support boundary conditions with polygonal action[J]. Journal of Sound and Vibration, 2015, (3): 1－9.

[20] Fung R F, Huang J S, Yeh J Y. Nonlinear dynamic stability of a moving string by Hamiltonian formulation[J]. Computers & Structures, 1998, 66(5): 597－612.

[21] Ghayesh M H, Amabili M, Paidoussis M P. Nonlinear vibrations and stability of an axially moving beam with an intermediate spring support: Two-dimensional analysis[J]. Nonlinear Dynamics, 2012, 70(70): 335－354.

[22] 任西春，王跃方. 基于Hamilton体系的弹性行进索精确模态分析[J]. 振动工程学报，2004，17(增刊2)：744－746. Ren Xichun, Wang Yuefang. Exact modal analysis of elastic, axially traveling cables based on Hamiltonian dynamics[J]. Journal of Vibration Engineering, 2004, 17(Supp2): 744－746. (in Chinese with English abstract)

[23] Nguyen Q C, Hong K S. Transverse vibration control of axially moving membranes by regulation of axial velocity[J]. IEEE Transactions on Control Systems Technology, 2012, 20(4): 1124－1131.

[24] Guo B Z, Jin F F. The active disturbance rejection and sliding mode control approach to the stabilization of the Euler– Bernoulli beam equation with boundary[J]. Automatica, 2013, 49(9): 2911－2918.

[25] Liu Y, Zhao Z, He W. Stabilization of an axially moving accelerated/decelerated system via an adaptive boundary control[J]. ISA Transactions, 2016, 64: 394－404.

[26] 李君，薛坤鹏，杨洲，等. 一种链式货运索道减振装置及方法：ZL201510812640.7[P]. 2016-02-17.

[27] 李君，杨洲，洪添胜，等. 一种链式货运索道水平调节减振装置及方法：ZL201310157004.6[P]. 2013- 08-02.

[28] 李君，杨洲，洪添胜，等. 一种链式货运索道垂直调节减振装置及方法：ZL201310156504.8[P]. 2013- 09-04.

[29] 李君，薛坤鹏，杨洲，等. 山地果园链索运送装备运动传感系统设计[J]. 农机化研究，2017，39(6)：79－84, 95. Li Jun, Xue Kunpeng, Yang Zhou, et al. Motion sensing system of chain equipment for hilly orchard[J]. Journal of Agricultural Mechanization Research, 2017, 39 (6): 79－84, 95. (in Chinese with English abstract)

李 君，薛坤鹏，杨 洲，洪添胜.果园货运链索横向振动非线性控制[J]. 农业工程学报，2017，33(23)：66－72. doi：10.11975/j.issn.1002-6819.2017.23.009 http://www.tcsae.org

Li Jun, Xue Kunpeng, Yang Zhou, Hong Tiansheng. Nonlinear transverse vibration control of orchard conveying chain system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(23): 66－72. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.23.009 http://www.tcsae.org

Nonlinear transverse vibration control of orchard conveying chain system

Li Jun1,2, Xue Kunpeng3, Yang Zhou1,2※, Hong Tiansheng1,2

(1.510642,; 2.510642,; 3.510630,)

Vibrations associated with motion can degrade the performance of transport systems in orchards. It is important to suppress vibrations which are subjected to varying parameter and boundary disturbance. Early research on the vibration reduction in continuously moving systems was focused on the passive control methods by changing the mass or stiffness to absorb vibrational energy. To improve the effectiveness of vibration controller, many active control methods have been proposed with actuating mechanisms to compute the control effect. The application of conveying chain system was proved to be labor-saving and high efficientin mountainous orchards. Unlike a moving string system, the conveying chain system in the orchard is more complicated in the structure and boundary excitation. When the chain link engages a sprocket tooth,there is an impact caused by polygonal action.The polygonal action results from the chain-support engagement and its resulting vibrations are the source of most of the noise. Moreover, it is inconvenient to mount actuators on the conveying chain system. Since the boundary control technique requires relatively few sensors and actuators, a particular actuator as the control mechanism was attached and coupled to the boundary of the moving chain.The control force was applied by the actuator with negligible dynamics, which was used to reduce the energy of the moving chain while dissipating the energy of a short length of the chain. An image acquisition device was used to measure the transverse displacement of the observation point. The actuator was activated when the vision sensor indicated that the chain vibration has occurred. The behavior of transverse vibration could be predicted by a two-dimensional model in a vertical plane. Then the mathematical model of the coupled chain system including the actuator dynamics was derived by using Hamilton’s principle, which could be represented by the nonlinear partial differential equations after the constraints had been applied. The Lyapunov method illustrates that the states of the system will ultimately travel to an equilibrium point if the total energy is dissipating. The energy dissipation strategy was extended to the chain model considering the polygon effect. In the controlled span part, the Lyapunov method was proposed to design the force control law for ensuring the vibration reduction in one span. Based on the total vibration energy of the moving chain, an energy-based Lyapunov function candidate was defined, which assured the dissipation of the vibration energy. To assure the asymptotical stability of the closed-loop system, a force control law was analyzed to determine the control force under the conditions of unknown disturbance and known disturbance. The proposed control force aimed to enforce this span part to be stationary or vibrate with a small amplitude. The comparison of the vibration amplitude at mid-span point under the controlled condition and uncontrolled condition clearly demonstrated that the vibration of chain part decreased much faster with the controller. The asymptotic exponential stability of moving chain system is proved by using the boundary force controller. The performance of the chain control system depends on force control law with guaranteed stability as well as actuator placement. Both simulation and experimental results confirm the feasibility of vibration suppression.

agricultural machinery; transportation; vibrations; mountainous orchard; chain; actuator; Lyapunov method; vibration control

10.11975/j.issn.1002-6819.2017.23.009

S229+.1; TD527

A

1002-6819(2017)-23-0066-07

2017-07-17

2017-11-07

国家自然科学基金项目（51205139）；农业部农业科研创新团队项目（农办人[2015]62 号）；广东省岭南水果产业技术体系创新团队建设项目（2017LM1107）

李 君，湖南永州人，教授，主要从事现代农业装备与机械化研究。Email：autojunli@scau.edu.cn

杨 洲，山西襄汾人，教授，博士生导师，主要从事农业机械化研究。Email：yangzhou@scau.edu.cn