Mathstudio在弦振动实验研究中的应用
2021-12-30蔡春雨李鸿明韩元春萨仁高娃程玉梅苗秀娟赵翠兰
蔡春雨,李鸿明,韩元春,萨仁高娃,程玉梅,苗秀娟,赵翠兰
(内蒙古民族大学 数理学院,内蒙古 通辽 028000)
由于弦振动实验既可以锻炼学生作图能力、分析和解决问题能力,又利于培养学生创新能力和探索精神,因此,对该实验的研究始终是教学研究的热点之一[1-6]。利用弦振动实验装置测量了弦线的波长[7]和线密度[8]、悬挂固体的密度[9]和浸入液体的密度[10,11]。使用最小二乘法,origin或matlab对弦振动实验进行了一系列研究[7,12-16]。Mathstudio以其便捷、高效、专业的特点,已逐渐应用在大学物理实验和数学的教学领域[17-22]。尽管弦振动实验如此重要,mathstudio又有这么多优点,但是从未有学者将二者结合起来。在大学物理实验教改背景下[23-25],为了助力大学物理实验课程改革,本文研究了mathstudio在验证弦振动规律和基于弦振动实验做进一步测量方面的应用,并与现有文献结果做了对比分析。
1 弦振动实验原理
在一根拉紧的弦线上,张力为T,线密度为ρ线,则沿弦线传播的横波应满足方程:
(1)
其中,x为波在传播方向上的位置坐标,y为弦线上各点的振动位移;
(2)
假设弦线的振动频率为f,横波波长为λ,则波速理论值为:
u=λ·f
(3)
联立式(2)与式(3),得波长:
(4)
上式可利用驻波原理得出。由驻波实验规律知,当弦线两个固定端之间距离L等于半波长整数倍时,就能形成驻波,记为:
(5)
式中n为弦线上驻波的半波数。
2 Mathstudio在弦振动实验中的具体应用
2.1 验证弦振动规律的正确性
将式(4)两边取自然对数:
(6)
接下来,将分两种情况来验证弦振动规律。
1) 弦线线密度和振动频率不变情况下
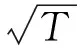
采用文献[14]中的研究数据,利用mathstudio,图1显示了弦线张力和波长的自然对数的关系。
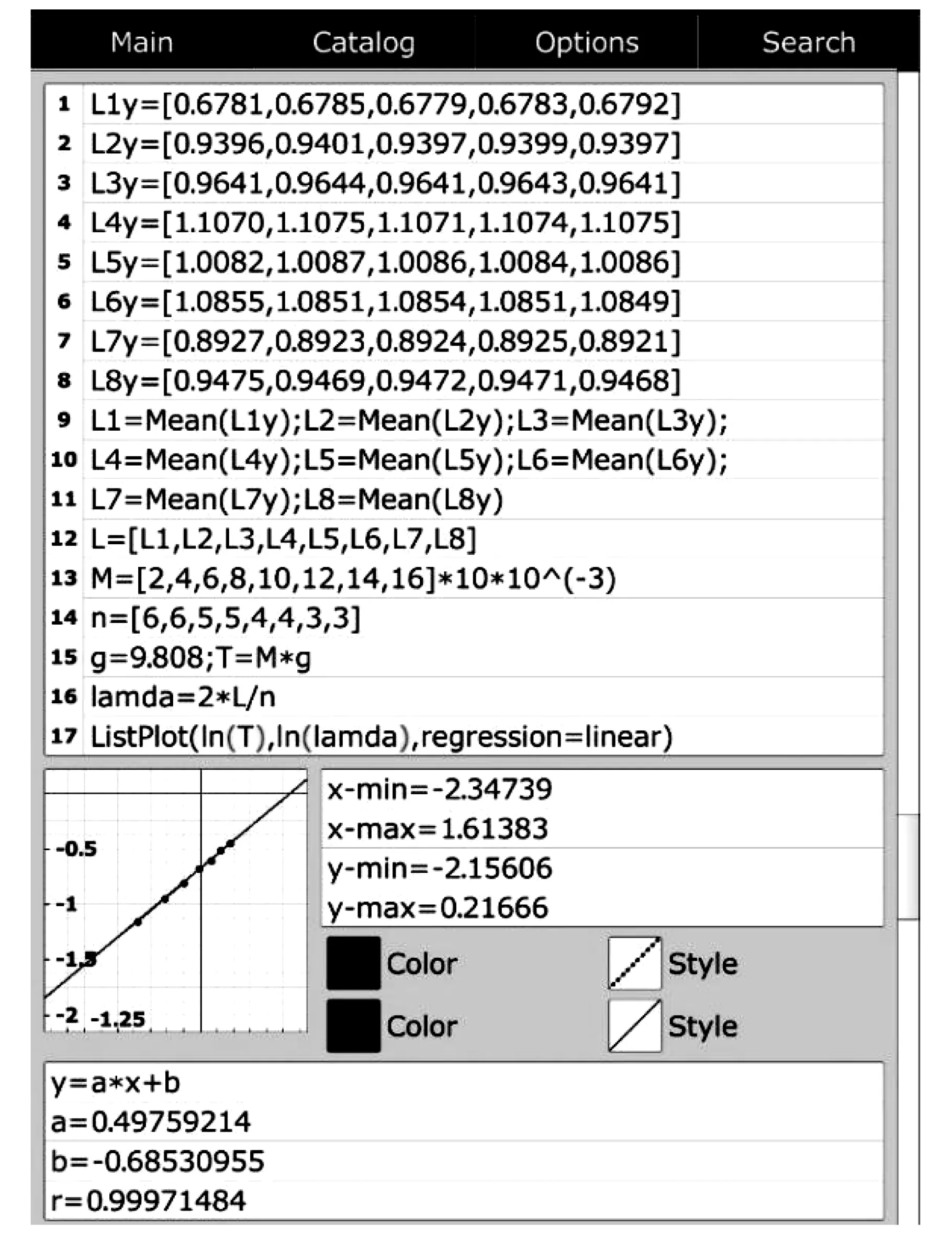
图1 ρ线和f一定情况下,利用mathstudio拟合文献[14]中lnT~lnλ关系
从图1中可以看出,mathstudio所拟合lnT~lnλ直线的斜率为0.497 592 14,与文献[14]用最小二乘法所得结果一致;另外,本文所得结果具有更高精度,且相关系数更接近1,因此拟合效果更好。由于mathstudio仅反馈程序最后一行命令的结果,因此,在图1的基础上,图2展示了文献[14]中作图所需的其他相关数据信息,与文献[14]中结果相同。相比文献[14]中用origin软件绘图的方式,用mathstudio计算文献[14]中弦振动相关数据的方法,更便捷、效率与精度更高。
2) 弦线线密度和张力不变情况下
在这种情况下,通过测量弦线在不同振动频率f下的波长λ,并以lnf为横坐标、lnλ为纵坐标,作lnf~lnλ图像,若得一斜率值为-1的直线,则验证了式(4)中λ与f成反比的规律。
在T=49.720 N,ρ线固定的情况下,以文献[16]中实验数据为例,利用mathstudio拟合的lnf~lnλ关系,如图3所示。容易看出:①图3中拟合直线的斜率为1.023 478,非常接近1,拟合效果很好地验证了式(4)中λ与f成反比的规律;②在验证式(4)正确性方面,图3比文献[16]中使用Matlab软件绘制的f~λ图像更恰当、更具说服力。
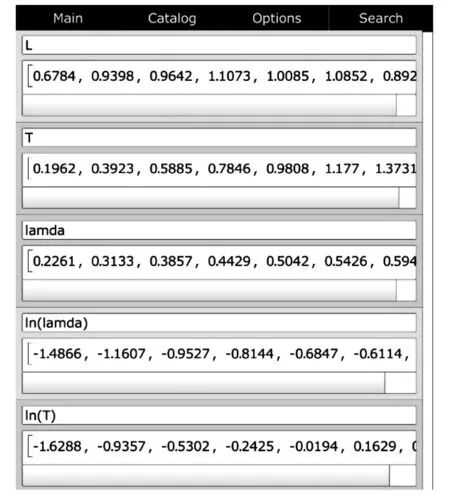
图2 在图1基础上,用mathstudio输出绘制lnT~lnλ图像所需数据
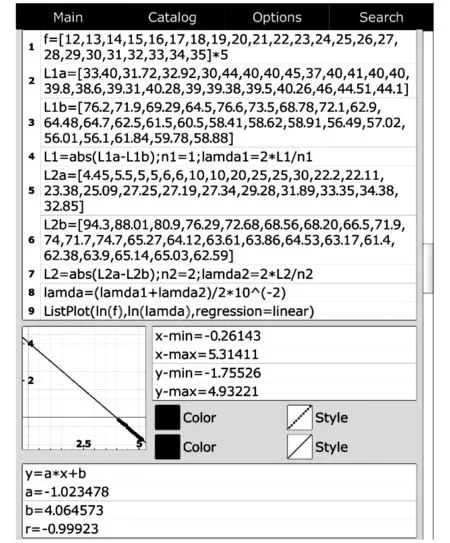
图3 T=49.720 N,ρ线固定的情况下,利用mathstudio拟合文献[16]中lnf~lnλ关系
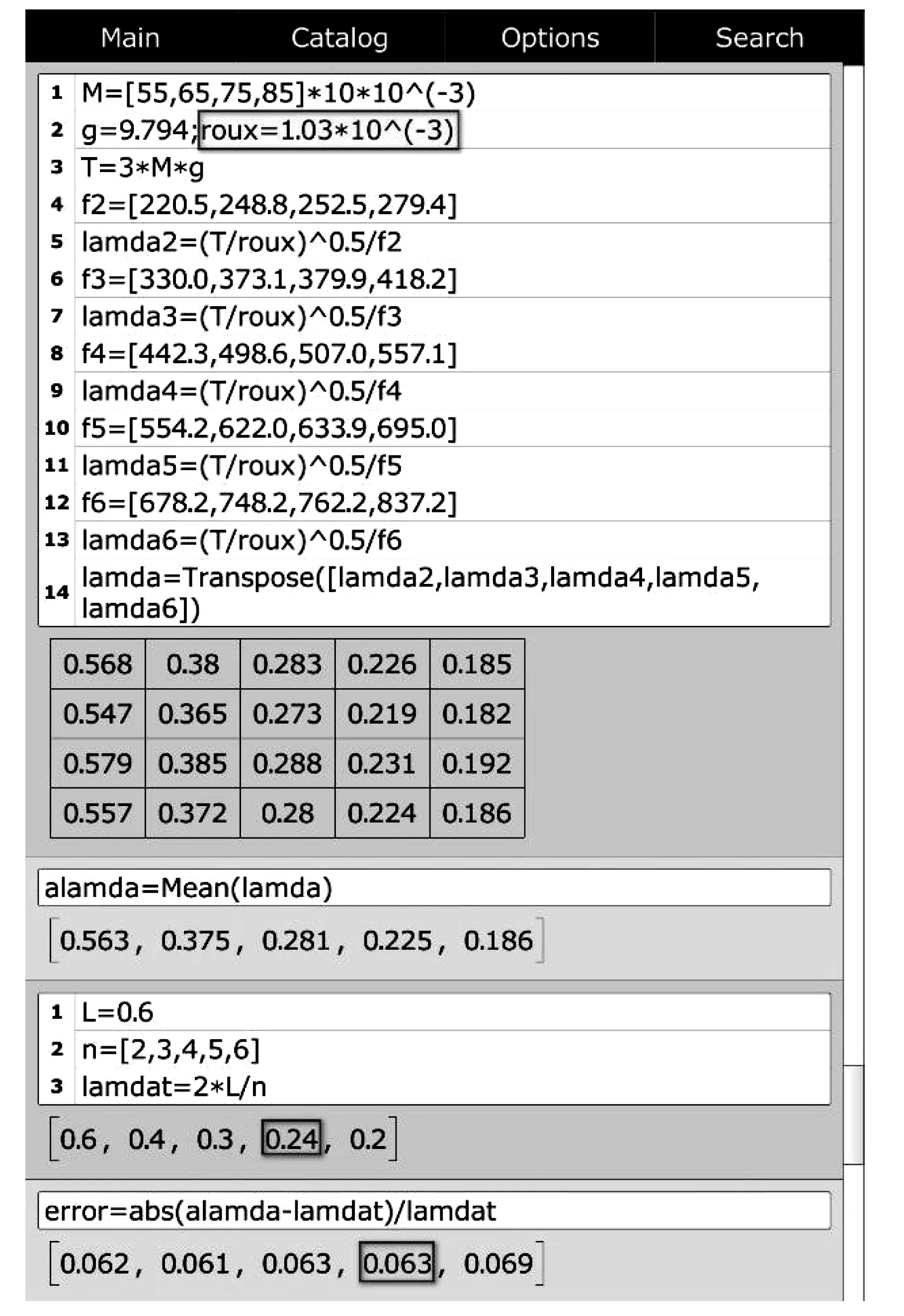
图4 利用mathstudio直接计算文献[7]中弦线波长及其误差
2.2 利用弦振动实验做进一步测量
基于弦振动实验,本节将展示如何利用mathstudio计算弦线波长与线密度以及浸入液体和悬挂固体的密度。
1) 测量弦线波长
本节利用mathstudio分别使用直接法和作图法计算了弦线波长,并将运算结果与文献[7]中结果做了对比分析。
(1) 直接计算弦线波长
由第1节弦振动实验原理知,弦线波长可由式(4)和式(5)分别求出。以文献[7]中数据为例,图4展示了利用mathstudio直接计算弦线波长及其相对误差的全部过程。本文所得结果与文献[7]中的结果一致。
(2) 作图法计算弦线波长
文献[7]提出了利用作图法测量弦线波长的方法。受其启发,本小节利用mathstudio和文献[7]中实验数据,拟合lgT~lgf的变化关系,来测量弦线波长,如图5所示。
由图5看出,lgT~lgf拟合直线的相关系数为0.999 002,拟合效果很好,从侧面再次验证了弦振动规律的正确性。同时,图5剩下的两行命令,计算、输出了文献[7]中用origin拟合、绘制lgT~lgf图像所需的数据,与文献[7]中结果相同,展示出mathstudio在计算和输出数据方面的强大与便捷。
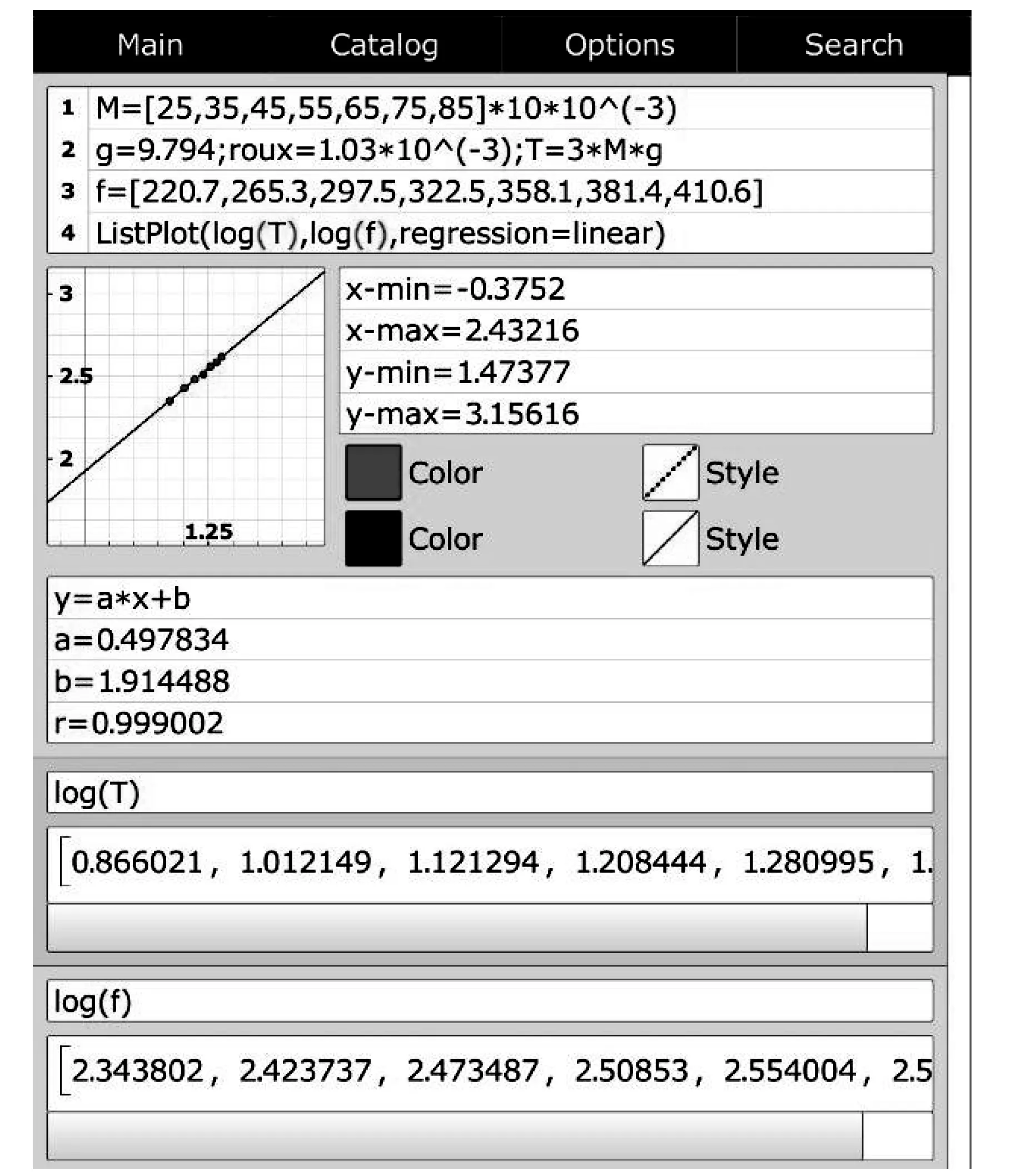
图5 l=0.6 m,n=3时,利用mathstudio拟合文献[7]中lgT~lgf的关系
利用图5中lgT~lgf拟合直线的截距,图6展示了使用mathstudio进一步计算弦线波长和弦线两个固定端之间的距离的理论值及其与实验值相对误差的详细过程。计算结果表明,弦线波长和弦线两个固定端之间的距离的理论值与其实验值的相对误差是相同的,均为5.150 9%,与文献[7]中用origin拟合、运算的结果一致。
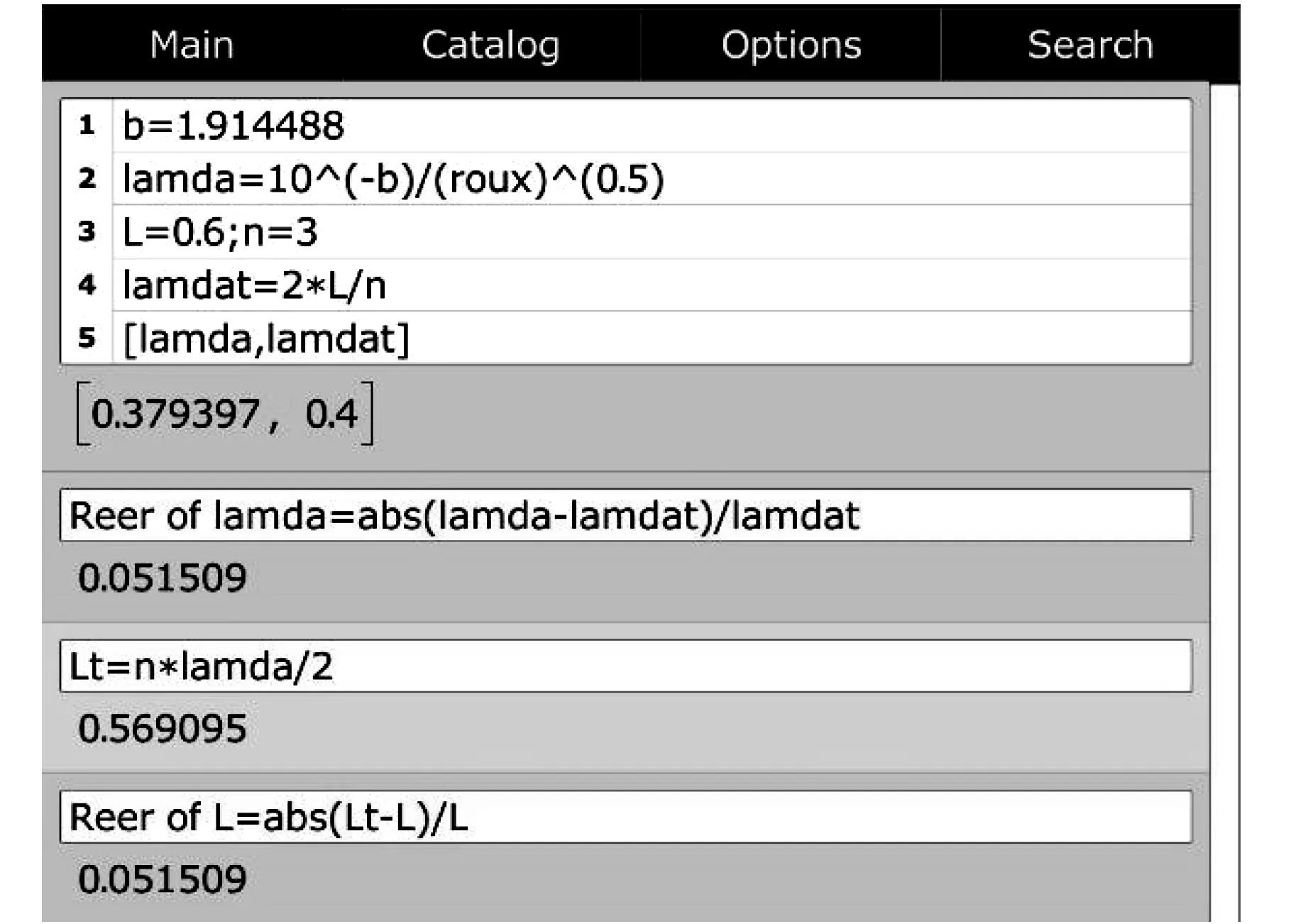
图6 在图5的基础上,继续利用mathstudio和作图法计算、输出文献[7]中弦线波长和两个固定端之间的距离及其与实验值的相对误差
2) 测量弦线的线密度
本节将分三种情况展示mathstudio在测量弦线线密度中的具体用法,并将计算结果与现有文献做了对比分析。第一种情况基于弦线线密度的定义,利用mathstudio直接对其进行计算;第二和三种情况,是在2.1节验证弦振动规律的基础上,进一步利用所拟合直线的截距信息,计算弦线的线密度,一方面弥补了弦振动该方面的研究,另一方面,对比分析了mathstudio运算结果与其他软件或方法所得结果。
(1) 直接计算弦线线密度的情况
根据弦线线密度的定义:

(7)
其中,m和L原分别表示弦线的总质量和当弦线中张力为零时弦线的总长度。
以文献[14]中数据为例,利用mathstudio直接计算弦线ρ线的程序,如图7所示。从图容易看出,本文所得结果与文献[14]中结果完全一致;同时,图7中上、下两部分内容的对比分析,展示了用mathstudio进行单位换算的便捷性。

图7 利用mathstudio直接计算文献[14]中弦线线密度
(2) 固定弦线线密度和振动频率情况下
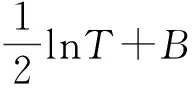
(8)
图8展示的是利用式(8)计算文献[13]中弦线线密度的程序。由于文献[13]未提供弦线线密度信息,而本文使用mathstudio发掘了该文献弦振动实验数据中的隐藏信息。

图8 ρ线和f一定情况下,利用mathstudio计算文献[13]中弦线的线密度
(3) 固定弦线线密度和张力情况下
在2.1节第2)部分的基础上,将式(6)与lnλ=-lnf+B′对比,利用lnf~lnλ拟合直线的截距B′,就可以通过下式计算该弦线的线密度:
=T·e-2B′
(9)
在图3基础上,图9展示了计算文献[16]中弦线线密度的过程。因文献[16]中未给出ρ线相关参数,但本文在ρ线和T一定情况下,利用lnf~lnλ图的截距信息,发掘了文献[16]中的隐藏信息,一方面拓展了弦振动实验的研究,另一方面通过mathstudio在物理实验中的运用,提升和培养了学生的学习兴趣和创新能力。
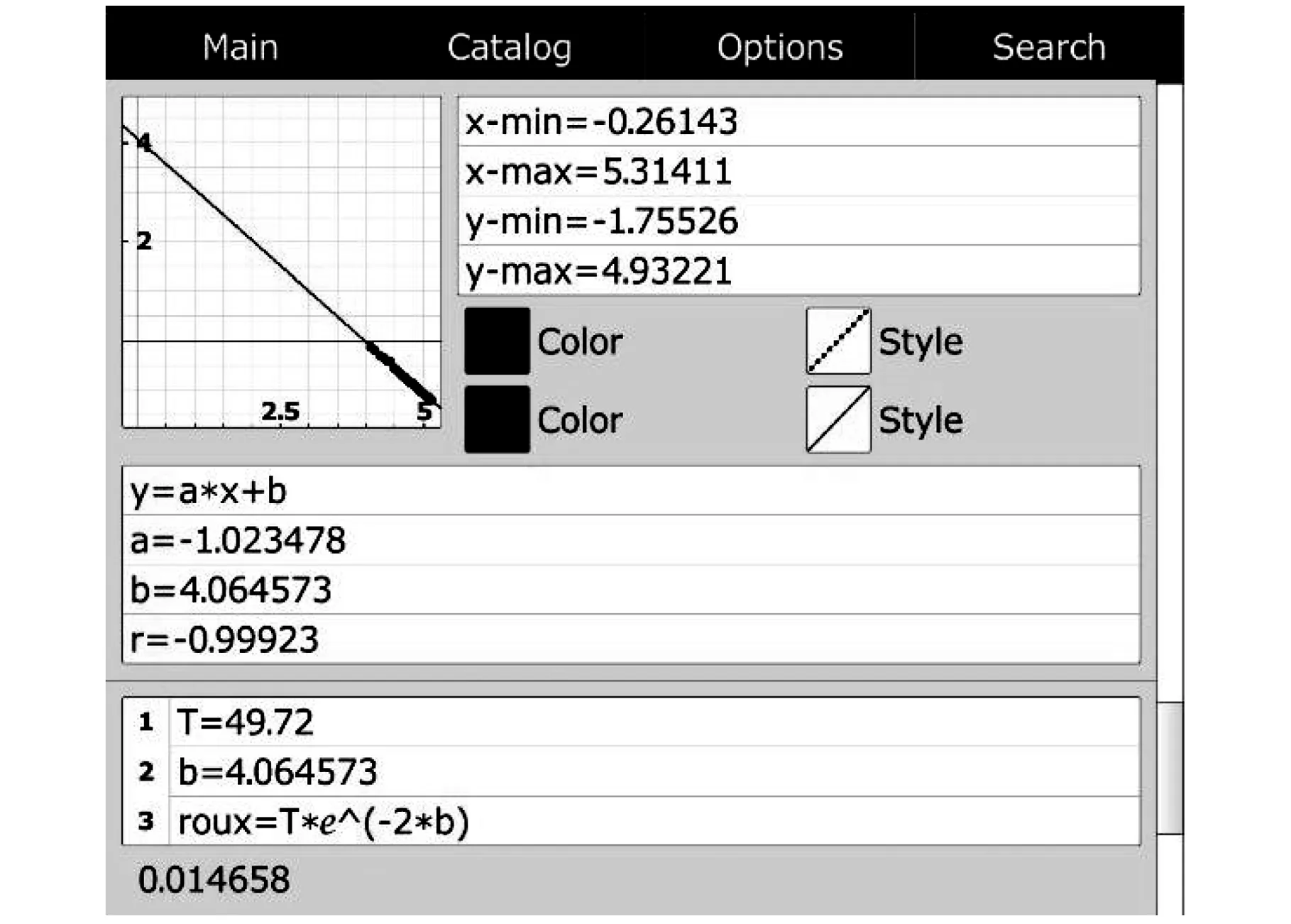
图9 ρ线和T一定情况下,利用mathstudio计算文献[16]中弦线的线密度
3) 进一步测量密度
通过巧改弦振动装置,本小节利用弦振动实验进一步测量浸入液体的密度以及弦线下方悬挂固体的密度。另外,在测量浸入液体密度的同时,又在其他参数相同的情况下,利用L2~M图像的斜率,拓展了弦线线密度的测量方法。
(1) 测量浸入液体的密度
图10显示的是测量浸入液体密度的装置图[11]。由该图可知弦线上的张力:
T=Mg-ρ液gV排
(10)
将上式与式(2,3&5)联立,得弦线上所拉砝码及其附件的总质量M:
(11)

图10 巧改弦振动实验装置测液体密度
当弦线固定、弦线的振动频率和半波数分别满足f=100Hz和n=1时,测得挂在弦线上不同质量M下弦线的两个固定端之间的距离L,若以L2为横坐标,M为纵坐标,由拟合直线的截距B‴,可间接求出待测液体的密度为:
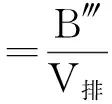
(12)
同时,在此基础上,利用拟合直线的斜率k,可进一步测量弦线的线密度:
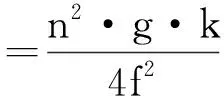
(13)
在ρ线一定、f=100Hz、n=1情况下,图11~图13展示了用mathstudio计算文献[11]中水、丙醇和甘油三种液体密度的全过程,所得结果与文献[11]中用回归法所得结果一致;同时,本文结果不仅具有更高精度,且相似问题仅需更换相应数据即可完美解决,大大提升了实验数据处理效率;虽然文献[11]未给弦线的线密度,但是,利用mathstudio和式(13),文献[11]中的实验数据为我们提供了测量弦线线密度的机会。因此,本文还利用mathstudio拟合图像的斜率信息,进一步计算了弦线的线密度。经mathstudio计算的文献[11]中弦线线密度的最大相对误差和平均值分别约为1.482%和0.000 106 61kg/m,如图14所示。

图11 ρ线一定、f=100 Hz、n=1时,利用mathstudio计算文献[11]中样品“水”的密度和弦线线密度
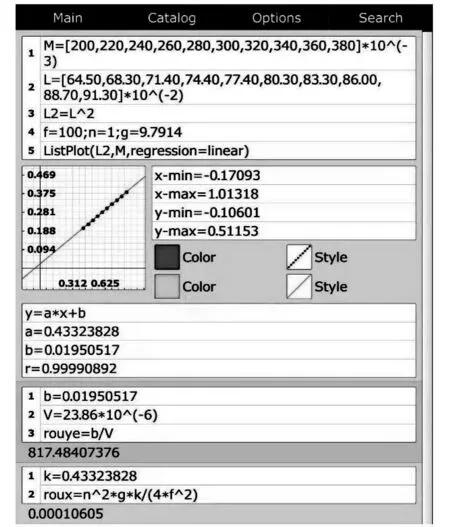
图12 ρ线一定、f=100 Hz、n=1时,利用mathstudio计算了文献[11]中样品“丙醇”的密度和弦线线密度

图13 ρ线一定、f=100 Hz、n=1时,利用mathstudio计算文献[11]中样品“甘油”的密度和弦线线密度
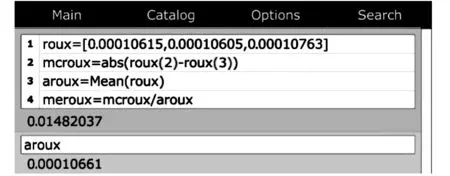
图14 ρ线一定、f=100 Hz、n=1时,利用mathstudio计算文献[11]中弦线线密度的最大相对误差及其平均值
(2) 测量悬挂固体的密度
测量装置仅需将普通的弦振动实验装置弦线下所挂砝码及其附件替换为待测固体即可。此时,弦线中的张力近似等于其悬挂固体的重力:
T=ρ固gV
(14)
将上式与式(2,3&5)联立,可得弦线下方悬挂固体的密度:
(15)
当n=2时,利用mathstudio计算了文献[9]中的实验数据。尽管文献[9]中采用三根弦线对同一固体的密度进行测量,但mathstudio仅用了13行命令,便完成了文献[9]中的全部计算,如图15所示,本文所得结果与文献[9]中的结果一致,且计算效率更高、更便捷。
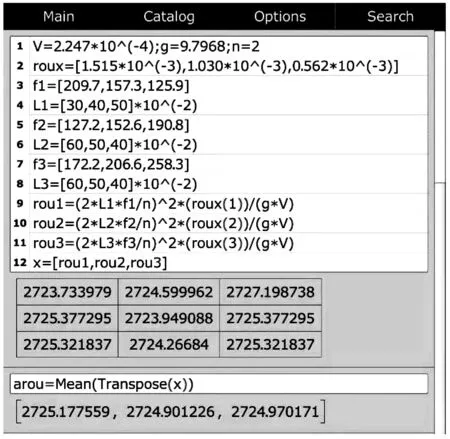
图15 n=2时,利用mathstudio计算文献[9]中悬挂固体的密度
4 结 语
本文利用mathstudio研究了现有弦振动实验文献中的实验数据,得到如下结论:①利用控制变量法和mathstudio,分两种情况验证了弦振动规律;②基于弦振动实验及规律,利用mathstudio拟合了相关实验数据,并基于所拟合直线的斜率或截距,计算了弦线的波长、线密度以及浸入液体和弦线上悬挂固体的密度,并与现有文献做了对比分析。总之,通过mathstudio在弦振动实验中的应用,不仅拓宽了弦振动实验的研究内容,还提升了学生的学习兴趣和动手能力,是我校大学物理实验教学的一个亮点,为探索大学物理实验教学与课程改革提供一定的参考价值。
