齿面摩擦激励对面齿轮传动系统振动特性的影响

冯仕伟，何国旗，王其雷，孙 能，邓澍杰

（湖南工业大学 机械工程学院，湖南 株洲 412007）

齿面摩擦激励对面齿轮传动系统振动特性的影响

冯仕伟，何国旗，王其雷，孙 能，邓澍杰

（湖南工业大学 机械工程学院，湖南 株洲 412007）

以正交面齿轮传动系统为研究对象，建立了考虑齿面摩擦激励的面齿轮传动系统非线性动力学模型，基于4～5阶的自适应变步长的龙格库塔法对该模型进行数值仿真求解，结合分岔图、时间历程图、poincare图等分析齿面摩擦系数对系统的振动特性的影响，并研究不同参数对系统响应发生倍周期分岔时摩擦系数临界点的影响。结果表明：系统响应随齿面摩擦系数的增大依次呈现出单周期简谐响应、倍周期次谐响应、混沌响应；面齿轮齿宽和圆柱齿轮驱动扭矩越大，系统响应发生倍周期分岔时的摩擦系数临界点数值越大，且随着齿宽和驱动扭矩的增大，其摩擦系数临界点变化曲线斜率越小，驱动扭矩对其变化曲线斜率较齿宽影响大；面齿轮齿数和系统齿侧间隙越大，系统响应发生倍周期分岔时的摩擦系数临界点数值越小，其摩擦系数临界点变化曲线斜率随面齿轮齿数增大而减小，而齿侧间隙对其变化曲线斜率基本没有影响 。

面齿轮传动；非线性动力学；摩擦系数；振动特性

0 引言

面齿轮传动具有重合度高、噪声低、振动小等许多优点，随着科技的不断发展，面齿轮传动因其独特的分流特性，使得其在航空领域尤其是在新型战斗直升机中的应用，表现出潜在的优势[1-5]。齿轮传动系统的振动和噪声一直是学界研究的重点，其中，作为系统内部激励的齿面摩擦是齿轮非线性振动的重要影响因素，其动态效应对系统振动、齿面磨损和齿轮寿命有着密切影响。因此，有必要深入研究齿面摩擦激励特性及其对系统动力学响应的影响。

目前，对于圆柱齿轮和锥齿轮传动系统的齿面摩擦激励及其对系统动力学特性影响的分析，已有较多学者进行了研究[6-9]。靳广虎等[10]建立了包含传递误差的面齿轮传动系统振动模型，研究传递误差对系统动态特性的影响；杨振等[11-12]建立了含时变啮合刚度、齿侧间隙和传递误差等因素的正交面齿轮传动系统非线性动力学模型，分析了啮合频率、齿侧间隙、时变啮合刚度、啮合阻尼和支撑刚度等参数对系统振动特性的影响；但关于面齿轮齿面摩擦激励机理及其对系统动力学特性影响的研究较少。

本文以正交面齿轮传动系统为研究对象，建立了考虑齿面摩擦激励的系统非线性动力学模型，基于龙格库塔法对该模型进行数值仿真求解，结合分岔图、时间历程图、poincare图等分析齿面时变摩擦系数对系统振动特性的影响，并研究面齿轮齿数和齿宽、圆柱齿轮驱动扭矩、系统齿侧间隙等参数对系统响应发生倍周期分岔时摩擦系数临界点的影响。

1 面齿轮传动系统非线性动力学模型

根据集中参数理论建立面齿轮传动系统的动力学模型，如图1所示。建模时进行以下处理：1）各坐标轴没有摆转振动；2）轴向间误差对系统的影响忽略不计；3）两齿轮采用具集中质量和转动惯量的圆柱体模拟，支撑轴承采用弹簧模拟；4）齿轮轴为刚性的，轴两端支撑等效处理到两齿轮轮心上。

所建立的模型以圆柱齿轮轴线为X轴，面齿轮轴线为Y轴，两轴线交点为坐标原点，建立直角坐标系Σ（O, X, Y, Z）。根据面齿轮传动特点和啮合原理，圆柱齿轮无轴向作用力，面齿轮无径向作用力，因此，只考虑两个坐标轴Y、Z方向上的阻尼和支撑，整个系统共有6个自由度，分别为两齿轮轮心沿Y、Z轴方向的平移自由度和转动自由度，表示为

式中：Yp、Zp分别为圆柱齿轮在Y、Z方向的平移自由度；θp为圆柱齿轮的转动自由度；Yg、Zg分别为面齿轮在Y、Z方向的平移自由度；θg为面齿轮的转动自由度。

图1 面齿轮传动系统非线性动力学模型Fig. 1 A nonlinear dynamic model of face-gear drive system

图1所示模型中：Op、Og分别为圆柱齿轮和面齿轮的轮心；Tp、Tg分别为两个齿轮的扭矩；θp、θg分别为两齿轮的扭角位移；kYp、kZp分别为圆柱齿轮在Y、Z方向的轴支撑刚度；kYg、kZg分别为面齿轮Y、Z方向的轴支撑刚度；Kh为时变啮合刚度；cYp、cZp分别为圆柱齿轮在Y、Z方向的轴承支撑阻尼；cYg、cZg分别为面齿轮在Y、Z方向的轴承支撑阻尼；ch为啮合阻尼；bYp、bZp分别为圆柱齿轮在Y、Z方向的轴承径向间隙；bYg、bZg分别为面齿轮在Y、Z方向的轴承径向间隙；bh为齿轮副法相间隙；eh为静态传递误差。

2 齿面时变摩擦力分析

在啮合中，齿面摩擦力的方向始终相切于两齿轮的啮合齿面，即与啮合线的方向垂直，如图2所示，其中ωp、ωg分别为圆柱齿轮和面齿轮的角速度。节点P处的摩擦力因相对滑动速度为零的原因而也等于零，且因过节点P处的相对滑动速度方向发生改变的缘故摩擦力方向也会发生改变[13]。因此，即使啮合力保持不变，啮合齿轮对间的摩擦力也会发生周期性改变。

图2 齿面摩擦力分析Fig. 2 An analysis of tooth face friction force

基于Coulomb摩擦定律，摩擦力大小正比于正压力，可得啮合点M处的摩擦力为[14]式中：u(t)为时变摩擦系数；Fn为啮合点处法向正压力；sign(M)为符号函数；可定义为

3 面齿轮传动系统非线性动力学微分方程

因振动位移和误差，两齿轮齿面沿啮合点法向方向在啮合点处产生的相对位移λn为

式中：rp、rg分别为圆柱齿轮和面齿轮啮合点半径，rp=mz1/2，rg=mz2/2，其中，z1为圆柱齿轮齿数，z2为面齿轮齿数；αn为两齿轮的法向压力角；eh(t)为静态传递误差。

由于制造和安装过程中会产生误差，使啮合齿廓在传动过程中发生偏离而产生位移型激励，在不具备试验测试情况下，采用近似的简谐函数对静态传递误差进行模拟。数学表达式如下：

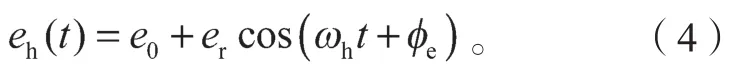
式中：e0为静态传递误差常量；er为静态传递误差变量幅值；ωh为啮合频率；为初始相位角。

根据受力分析，由牛顿定律可以得知啮合齿轮间的法向动载荷Fn及其沿坐标轴的分力FY、FZ分别为：

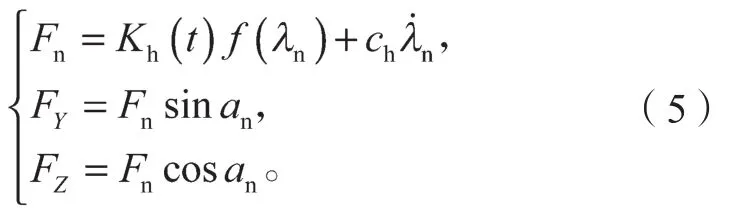
式中：Kh(t)为时变啮合刚度；f(λn)为间隙函数，可定义为

其中λn为相对位移。

考虑到齿轮轴的轴承支承同样存在一定的间隙，可以使用相同的间隙函数f(I, j)表示，则轴承支撑沿Y、Z方向的支撑力FIj可表示为：

式中：I为方向，可取值为Y和Z；j为齿轮类别，可取值为p和g（p代表圆柱齿轮，g代表面齿轮）；kIj为在I方向上齿轮j受到的支撑刚度。

面齿轮空载重合度一般在1.6～1.8，在单双齿啮合区域的交替处齿轮副综合啮合刚度会发生阶跃性突变；由于单双齿啮合区交替出现的影响，会使轮齿变形具有周期性，进而使齿轮副综合啮合刚度产生周期变化，可将其理解为由平均分量和单频的交变分量组成，数学表达式如下：

式中：Km为综合啮合刚度平均值；Kr为啮合刚度波动幅值；为初始相位角。

因此根据牛顿定律，图1所建立的面齿轮传动系统的振动动力学微分方程为：

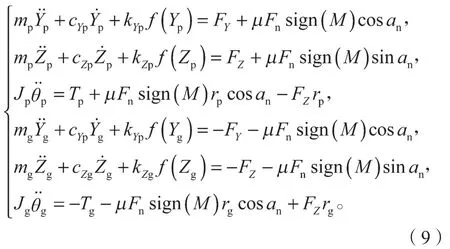
式中：mp、mg分别为圆柱齿轮和面齿轮的集中质量；Jp、Jg分别为圆柱齿轮和面齿轮的转动惯量；µ为齿面摩擦系数。

以两齿轮齿面沿啮合点法向方向在啮合点处产生的相对位移λn作为面齿轮传动系统新的自由度，对式（9）进行量纲一化处理，得出面齿轮传动系统无量纲化非线性动力学微分方程：

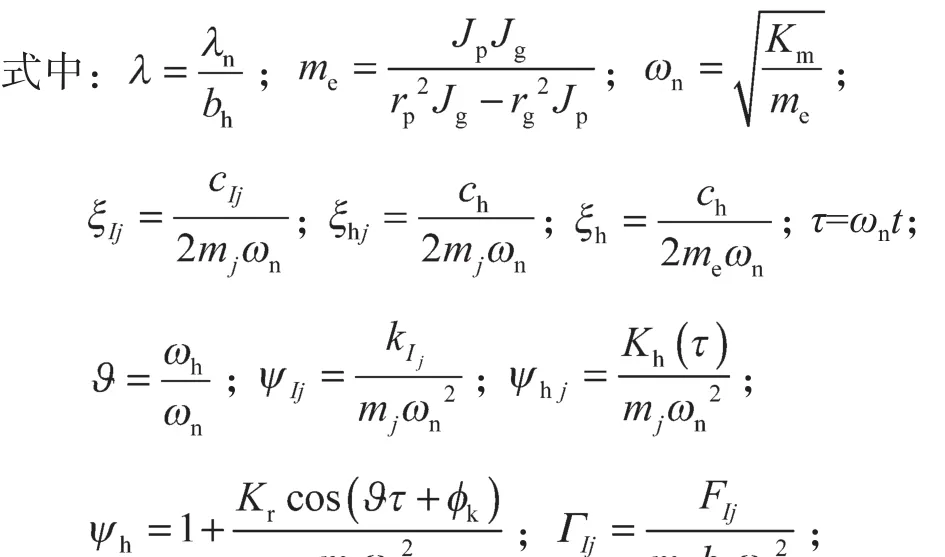
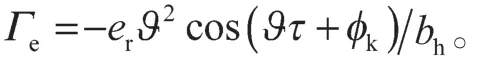
4 齿面摩擦系数对系统周期和混沌的影响

表1 面齿轮传动系统主要参数Table 1 Main parameters of the face-gear system

图3 摩擦系数μ变化时系统响应分岔图Fig. 3 A bifurcation diagram of system response with a changing friction coef fi cient μ

由图3可知，系统响应随着摩擦系数的增大依次呈现出单周期简谐响应、倍周期次谐响应、混沌响应。当摩擦系数继续增大时，混沌区域也随之相应扩大，系统响应表现出波动幅值较大、混乱无序的运动状态。

当摩擦系数µ为0.025时，系统呈现单周期简谐响应，具体的变化情况如图4所示，此时系统的时间历程图为单周期简谐运动，ponicare截面图为1个离散点。当摩擦系数µ增大到0.048时，系统开始呈现倍周期分岔现象。当摩擦系数µ为0.048～0.055时，系统呈现2倍周期次谐响应，具体情况如图5所示，此时系统的时间历程图为2T的周期运动，poincare截面图为2个离散点。当摩擦系数µ为0.055～0.062时，系统呈现4倍周期次谐响应，如图6所示，此时系统时间历程表现为4T周期运动，ponicare截面图为4个离散点。当摩擦系数µ继续增大，系统依次呈现8, 16, …倍周期次谐响应，对应的时间历程图依次为8T, 16T, …周期运动，ponicare截面图依次为8, 16, …个离散点，最终呈现出混沌响应，如图7所示。

图4 摩擦系数μ=0.025时的单周期简谐响应Fig. 4 Monocyclic simple harmonic response with the friction coef fi cient μ=0.025

图5 摩擦系数μ=0.05时的2倍周期次谐响应Fig. 5 Double sub-harmonic response with the friction coef fi cient μ=0.05

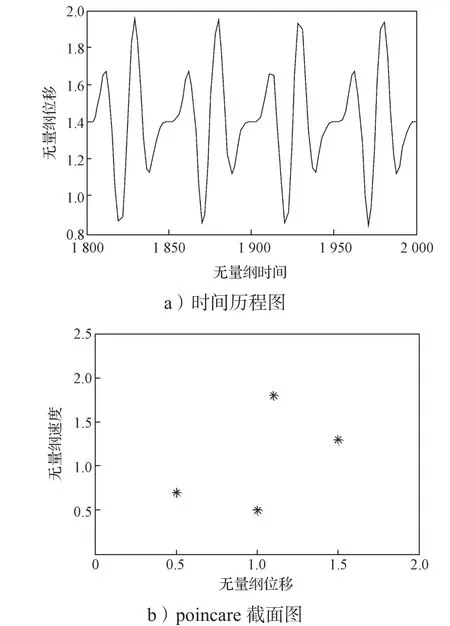
图6 摩擦系数μ=0.06时的4倍周期次谐响应Fig. 6 4 times sub-harmonic response with the friction coef fi cient μ=0.06

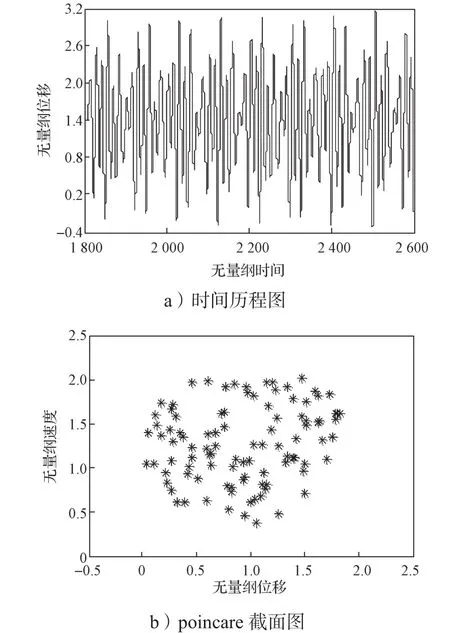
图7 摩擦系数μ=0.08时的混沌响应Fig. 7 Chaotic response with the friction coef fi cient μ=0.08

根据以上分析可知，齿面摩擦系数对面齿轮传动系统振动特性有重要影响，齿面摩擦激励的存在进一步增强了面齿轮传动系统的非线性振动响应特性。

5 不同参数对系统响应发生倍周期分岔时摩擦系数临界点的影响

为研究面齿轮齿数和齿宽、圆柱齿轮驱动扭矩、系统齿侧间隙等参数对系统响应发生倍周期分岔时摩擦系数临界点的影响，以面齿轮齿数和齿宽、圆柱齿轮驱动扭矩、系统齿侧间隙等参数分别作为单一变量进行分析，如表2所示。其余参数取表1中的数据，得出不同参数下系统响应发生倍周期分岔时摩擦系数临界点的数值，如图8所示。

表2 面齿轮传动系统的参数变化Table 2 Parametric variations of the face-gear drive system

图8 不同参数取值对系统响应发生倍周期分岔时摩擦系数临界点的影响Fig. 8 In fl uence of different parameters values on the critical point of friction coef fi cient for the period doubling bifurcation of the system response

由图8可知，面齿轮齿宽和圆柱齿轮驱动扭矩越大，系统响应发生倍周期分岔时的摩擦系数临界点数值越大，且随着齿宽和驱动扭矩的增大，其摩擦系数临界点变化曲线斜率越小，驱动扭矩对其变化曲线斜率较齿宽影响大；面齿轮齿数和系统齿侧间隙越大，系统响应发生倍周期分岔时的摩擦系数临界点数值越小，随着面齿轮齿数的增大，其摩擦系数临界点变化曲线斜率越小，而齿侧间隙的增大对其变化曲线斜率基本没有影响。

6 结论

以正交面齿轮传动系统为研究对象，建立了考虑齿面摩擦激励的系统非线性动力学模型，基于龙格库塔法对该模型进行数值仿真求解，分析了齿面时变摩擦系数对系统的振动特性的影响，并研究了面齿轮齿数和齿宽、圆柱齿轮驱动扭矩、系统齿侧间隙等参数对系统响应发生倍周期分岔时摩擦系数临界点的影响，得出了相应规律：

1）齿面摩擦系数对面齿轮传动系统的振动特性有重要影响，系统响应随齿面摩擦系数的增大依次呈现出单周期简谐响应、倍周期次谐响应、混沌响应；

2）面齿轮齿宽和圆柱齿轮驱动扭矩越大，系统响应发生倍周期分岔时的摩擦系数临界点数值越大，且随着齿宽和驱动扭矩的增大，其摩擦系数临界点变化曲线斜率越小，驱动扭矩对其变化曲线斜率较齿宽影响大；

3）面齿轮齿数和系统齿侧间隙越大，系统响应发生倍周期分岔时的摩擦系数临界点数值越小，其摩擦系数临界点变化曲线斜率随面齿轮齿数增大而减小，而齿侧间隙对其变化曲线斜率基本没有影响。

[1] LITIVIN F L，ZHANG Y，WANG J C，et al. Design and Geometry of Face-Gear Drive[J]. Journal of Mechanical Design，1992，114(4)：642-647.

[2] HANDSCHUH R，LEWICKI D，BOSSLER R.Experimental Tesing of Prototype Face-Gears for Helicopter Transmissions[R]. Solihull：NASA Technical Memorandum 105434，1992：1-10.

[3] LITVIN F L，CHEN N X，CHEN J S，et al. Computerized Deter-Mination of Curvature Relations and Contacr Ellipse for Conjugate Surfaces[J]. Computer Methods in Applied Mechanics & Engineering，1995，125(1/2/3/4)：151-170.

[4] 王其雷，何 瑛，何国旗，等. 基于ANSYS Workbench的面齿轮固有特性分析[J]. 湖南工业大学学报，2016，30(1)：1-5.WANG Qilei，HE Ying，HE Guoqi，et al. Analysis on Natural Vibration Characteristics of Face-Gear Drive Based on ANSYS Workbench[J]. Journal of Hunan University of Technology，2016，30(1)：1-5.

[5] 孙 能，何 瑛，何国旗，等. 面齿轮等温点接触弹流润滑分析[J]. 湖南工业大学学报，2016，30(1)：6-10.SUN Neng，HE Ying，HE Guoqi，et al. Analysis of Contact Elastohydrodynamic Lubrication on Isothermal Point of Face-Gear[J]. Journal of Hunan University of Technology，2016，30(1)：6-10.

[6] 张 靖，陈兵奎，康传章，等. 计及齿面摩擦的直齿轮动力学分析[J]. 振动与冲击，2012，31(21)：126-132.ZHANG Jing，CHEN Bingkui，KANG Chuanzhang，et al. Dynamic Analysis on the Spur Gears Considering Friction Effect[J]. Journal of Vibration and Shock，2012，31(21)：126-132.

[7] 李文良，王黎钦，常 山，等. 齿面摩擦对齿轮系统谐波共振的影响[J]. 吉林大学学报（工学版），2013，43(5)：1290-1294.LI Wenliang，WANG Liqin，CHANG Shan，et al.Impact of Tooth Surface Fraction on Harmonic Resonance of Gear System[J]. Journal of Jilin University(Engineering and Technology Edition)，2013，43(5)：1290-1294.

[8] 王 一，王奇斌，张义民. 基于齿面摩擦的斜齿轮传动动力学特性分析[J]. 机械设计与制造，2013(10)：22-25.WANG Yi，WANG Qibin，ZHANG Yimin. Helical Gear System Dynamic Character Analysis Based on Sliding Friction[J]. Machine Design & Manufacture，2013(10)：22-25.

[9] 冯治恒. 螺旋锥齿轮多体自由度非线性动力学研究[D]. 重庆：重庆大学，2010.FENG Zhiheng. Research on Multi-Body Multi-DOF Nonlinear Dynamic of Helical Bevel Gear[D].Chongqing：Chongqing University，2010.

[10] 靳广虎，朱如鹏，朱自冰，等. 正交面齿轮传动系统的耦合振动分析[J]. 机械科学与技术，2009，28(1)：124-132.JIN Guanghu，ZHU Rupeng，ZHU Zibing，et al.Analysis of the Coupling Vibration of a Face Gear Transmission System[J]. Mechanical Science and Technology for Aerospace Engineering，2009，28(1)：124-132.

[11] 杨 振，王三民，范叶森，等. 面齿轮传动系统参数激励振动特性分析[J]. 重庆大学学报（自然科学版），2011，34(1)：26-35.YANG Zhen，WANG Sanmin，FAN Yesen，et al.Vibration Characteristics of Face-Gear Transmission System with Parametric Excitation[J]. Journal of Chongqing University(Natural Science Edition)，2011，34(1)：26-35.

[12] 杨 振，王三民，范叶森，等. 正交面齿轮传动系统非线性振动特性研究[J]. 振动与冲击，2010，29(9)，218-221.YANG Zhen，WANG Sanmin，FAN Yesen，et al. Nonlinear Dynamics of Face-Gear Transmission System[J]. Journal of Vibration and Shock，2010，29(9)，218-221.

[13] 严宏志，胡 威，何国旗. 考虑表面粗糙度的面齿轮齿面接触应力分析[J]. 机械设计与研究，2012，28(4)：58-65.YAN Hongzhi，HU Wei，HE Guoqi. Contact Stress Analysis of Face-Gear Drive with Considering the Surface Roughness[J]. Machine Design and Research，2012，28(4)：58-65.

[14] 李 龙. 正交面齿轮传动的润滑分析[D]. 南京：南京航空航天大学，2007.LI Long. The Analysis of Lubrication of Orthogonal Face-Gear Drive System[D]. Nanjing：Nanjing University of Aeronautics and Astronautics，2007.

Research on the In fl uence of Tooth Surface Friction on Nonlinear Vibration Characteristics of the Face-Gear Drive System

FENG Shiwei，HE Guoqi ，WANG Qilei，SUN Neng，DENG Shujie
（School of Mechanical Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China）

Taking the orthogonal face gear drive system as the research object, a nonlinear dynamic model, in consideration of the tooth surface friction, has been established of the face gear drive system. A numerical simulation has been performed to solve the model by Runge Kutta method with variable step size adaptive 4～5 order based on the combination of bifurcation diagram, time history diagram, and poincare diagram to analyze the in fl uence of the vibration characteristics of gear tooth friction coef fi cient on the system, followed by a study on the in fl uence of different parameters with period doubling bifurcation on the critical point of friction coefficient. The results show that the response of the system increases positively with the increase of the friction coef fi cient of the tooth surface, successively making the system response in a state of a single period harmonic response, a period doubling subharmonic response and a chaotic response. The greater the gear tooth width and the driving torque of the cylindrical gear, the greater the critical coef fi cient of friction coef fi cient will be, with the system responding to the period doubling bifurcation. With the increase of tooth width and driving torque, the smaller the slope of the critical coef fi cient of the friction coef fi cient,the smaller the slope of the driving torque will be to the width of the tooth. The larger the number of face teeth and the greater backlash of the system, the smaller the critical point of the friction coef fi cient of the system will be when the period doubling bifurcation occurs. The slope of the friction coef fi cient critical point change curve decreases with the increase of the gear teeth number, with no in fl uence of the tooth side gap on the slope of its change curve.

face-gear drive；nonlinear dynamics；friction coef fi cient；vibration characteristic

TH132.41

A

1673-9833(2017)05-0065-07

10.3969/j.issn.1673-9833.2017.05.011

2017-05-22

国家自然科学基金资助项目（51375159，51575533），湖南省自然科学基金（株洲联合）资助项目（2015JJ5020）

冯仕伟（1993-），男，湖北石首人，湖南工业大学硕士生，主要研究方向为数字化制造理论与技术，E-mail：2278791919@qq.com

（责任编辑：申 剑）